甚高通量衛星通信系統多播場景線性預編碼算法

魏強 廖瑛 辛寧 張千 郝媛媛 任術波 繆中宇

(1 國防科技大學 空天科學學院,長沙 410073)(2 中國空間技術研究院通信與導航衛星總體部,北京 100094)

隨著高速互聯網業務的不斷發展,地球同步軌道(GEO)寬帶通信衛星系統從C頻段、Ku頻段寬波束向Ku頻段、Ka頻段點波束的高通量衛星發展,系統容量大幅提升,真正實現了互聯網高速接入[1-2]。高通量衛星最早是由美國航天咨詢公司提出的概念,將其定義為“采用多點波束和頻率復用技術、在相同頻率資源條件下整星容量大幅提升,達到傳統固定通信衛星的數倍、面向消費者互聯網接入等寬帶應用”的衛星。目前,高通量衛星已經成為衛星通信領域的熱點之一,包括中國在內的多個國家和地區已成功發射多顆高通量衛星,其中以中星26號衛星為代表的Ka頻段高通量衛星整星容量已超過百吉比特每秒[3]。

為進一步提升系統容量,下一代甚高通量衛星(VHTS)通信系統將采用更窄的波束、更高的頻率復用程度,但也更容易受到同頻干擾等影響。在全頻率復用的VHTS通信場景中,線性預編碼技術是一種很有潛力的干擾抑制技術[4-5]。針對基于幀的多播線性預編碼問題,文獻[6]中先通過半陣定放松法(SDR)和高斯隨機化獲取解耦的服務質量(QoS)問題的解,然后采用次梯度投影法進行功率再分配,二者交替優化直到問題收斂;相比于4色復用的方法和加權公平性算法,該線性預編碼技術可以顯著提升波束的平均吞吐量,但隨著波束內用戶數量的增加,每個波束的吞吐量會明顯下降。而且,上述線性預編碼的計算方法具有較高的復雜度。文獻[7]中提出一種中心化的方法,該方法通過連續凸近似的方式將原來非凸問題近似為迭代的二階錐規劃問題。文獻[8]中設計了一種基于和速率最大化的線性預編碼器,通過分布式的線性接收機將和速率最大化問題轉化成加權最小均方誤差最小化(WMMSE)問題,然后計算最小均方誤差(MMSE)接收機和加權值,進而通過迭代方式求解線性預編碼矢量。相比直接采用MMSE線性預編碼,該算法的吞吐量性能有顯著增加。然而,文獻[6-8]中均未考慮數字視頻廣播第2代擴展標準(DVB-S2X)中多播幀[9]的特點,部分算法的復雜度較高,不適用于VHTS通信系統。

由于前向信號是由信關站發射,且信關站更易獲取所有用戶的信道狀態信息,在前向鏈路進行預編碼設計更便于實際應用。因此,本文針對VHTS通信系統的前向鏈路,考慮星上功率約束,以最大化系統總吞吐量為目標,設計通信系統多播場景下的線性預編碼算法。考慮該優化問題的非凸性,將問題轉化成總的最差最小均方誤差(MSE)最小化問題,然后利用交替方向乘子法(ADMM)將其分解成多個并行子問題進行求解。仿真結果表明:在用戶分組尺寸較大時,本文算法相比于應用MMSE的算法具有顯著的吞吐量增益,且其計算復雜度較低。

1 系統模型

1.1 信道模型

VHTS通信系統工作在GEO,其信道受自由空間損耗、波束增益模式及其他附加損耗的影響。對于工作在10GHz以上的衛星信道,雨衰是對流層中大氣衰減的主要因素。

(1)自由空間損耗。自由空間損耗是指由于無線電波在空間傳播,電波能量隨著傳播距離增加而損耗,一般采用自由空間損耗系數來表征這種衰減,第i個波束的自由空間損耗系數可以表示為bmax(i)=[c/(4πf)]2/di2,其中,c為光速,f為頻率,di為衛星到第i個波束中心的距離。

(2)波束增益。影響信道質量的因素除了自由空間損耗,還有波束增益。在每個波束覆蓋區域內,處于中心點的用戶終端獲得的波束增益最大,其余位置的增益隨著與波束中心距離的增大而衰減,用戶的接收波束增益具體計算公式可參考文獻[10]。

(3)雨衰。由于天氣等氣象條件的影響,星地鏈路的信道質量還會受到一些附加的損耗影響,例如降雨導致的雨衰、大氣吸收損耗及電離層閃爍。對于10GHz以上的頻段,降雨導致的衰減更加嚴重,而本文采用的是Ka頻段,所以在信道建模時需要考慮雨衰對于信道質量的影響。根據國際電信聯盟無線電通信組(ITU-R)建議P.1853[11],定義雨衰系數矢量Ψik=[ψ1,ikψ2,ik…ψG,ik]T,那么第i個波束內第k個用戶的信道矢量可以表示為

(1)

式中:⊙為哈達瑪積;GT,GR分別為發送和接收的天線增益;κTB為噪聲功率,其中,κ為玻爾茲曼常數,T為接收機噪聲溫度,B為載波帶寬,為了便于計算,將噪聲功率歸一化到信道中計算;波束增益矢量bik=[b1,ikb2,ik…bG,ik]T;信道相位分量Φik=[φ1,ikφ2,ik…φG,ik]T,在[0,2π]服從均勻分布。

1.2 信號模型

第i個波束內第k個用戶的接收信號可以表示為

(2)

式中:l為除了i以外的波束;nik為噪聲。

基于DVB-S2X多播幀的特點,假設si為第i個波束的K個用戶數據所組成的數據幀信號,不同波束的信號相互獨立,且與噪聲nik獨立,wi為第i個波束的線性預編碼矢量,則第i個波束內第k個用戶的信干噪比(SINR)為

(3)

2 線性預編碼算法

2.1 和吞吐量最大化問題建立

本文研究的多播場景下線性預編碼以最大化系統總吞吐量為目標,并考慮星上功率約束。由于在該場景下每個波束內的數據構成一幀,每個波束的吞吐量由最差的用戶SINR決定,根據香農公式,最大化系統的總吞吐量就需要增大每個波束內最差用戶的SINR,因此,在考慮星上功率約束的情況下,多播場景下的線性預編碼優化問題表示為

(4)

從式(4)可以看出:該問題是一個非凸優化問題,需要將其轉化成凸優化問題來求解。文獻[8]中證明了和速率最大化問題可以轉換成WMMSE問題求解,而優化問題(4)與和速率最大化問題具有相似的結構,因此該問題也可以轉換成與WMMSE問題類似的問題求解,即

(5)

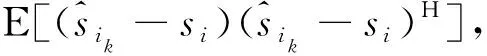
現在通過求解優化問題(5)來得到優化問題(4)的解。對于問題(5),可以看到問題中的優化變量有uik,wi,ti,采用迭代優化的方式求解。

(2)固定變量uik,ti,優化線性預編碼矢量wi,得到優化問題。

(6)

2.2 應用ADMM的線性預編碼設計

定義αi=maxEik(k∈),且引入3組輔助變量vi=wi,那么優化問題(6)可等價表示為

(7)

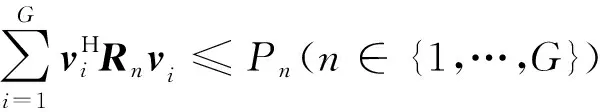
(8)

其拉格朗日形式為

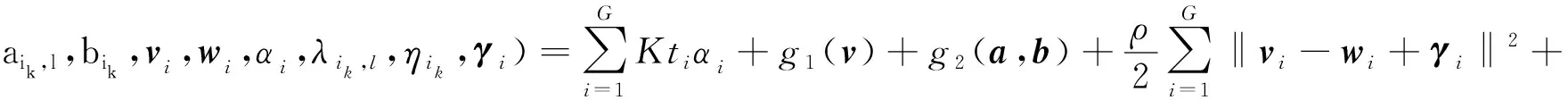
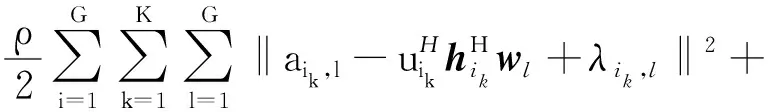
(9)

式中:懲罰參數ρ>0;λ定義為{λik,l|i,l∈{1,…,G},k∈{1,…,K}},η定義為{ηik|i∈{1,…,G},k∈{1,…,K}},γ定義為{γi∈CG|i∈{1,…,G}},分別表示式(9)中各個變量的縮放對偶變量。

分析式(9),可以將變量分成2組,即局部變量{v,a,b}和全局變量{w,α};同樣地,目標函數也可以分解,因此采用ADMM的算法來求解式(7),通過交替更新的方式對2組變量進行更新。

2.3 ADMM的變量更新

本節對各組變量的更新進行詳細的分析。

2.3.1 更新局部變量{v,a,b}

(10)

(11)

1)更新局部變量{v}

優化問題(10)可以等價為G個并行的子問題求解,每個子問題表示為

(12)

式中:vn,i,wn,i,γn,i分別為vi,wi,γi的第n個元素。

(13)

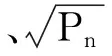
(14)

2)更新局部變量{a,b}

將優化問題(11)分解成GK個子問題并行求解,每個子問題表示為

(15)

其拉格朗日形式為

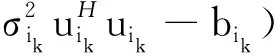
(16)

式中:對偶變量πik≥0。

用最優化理論中KKT條件求解優化問題(16),得到最優解為

(17)

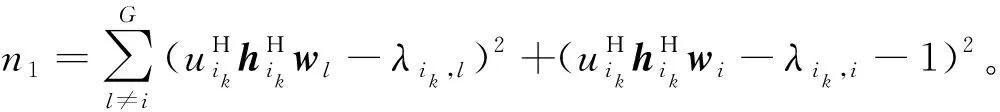
2.3.2 更新全局變量{w,α}

同樣,更新全局變量可以分解成2個優化問題,即

(18)

(19)

先求解優化問題(18),該優化問題同樣可以分解成G個并行子問題,每個子問題表示為

‖vl-wl+γl‖2

(20)

得到最優的線性預編碼矢量為

(21)

再求解優化問題(19),該問題同樣可以分解成G個并行的子問題,求得最優解為

(22)

2.3.3 更新對偶變量{λ,η,γ}

對偶變量采用次優梯度法進行更新,即

(23)

式中:迭代幅度值sj=1/j。

經過有限次迭代更新后,ADMM可以獲得最優的預編碼矢量,然后代入到式(6)中,更新MMSE接收機和加權值,重復該步驟,直到算法收斂。算法的主要實現流程如圖2所示。

2.4 算法復雜度分析

文獻[12]中已證明對偶變量求解的計算復雜度為對偶問題維度的多項式函數,并可利用次優梯度法在有限次迭代后達到收斂。此外,觀察上述算法步驟可知,在每次迭代過程中可通過閉式表達式(14),(17),(21),(22)得到最優解。因此,可以證明本文算法為多項式級計算復雜度并保證收斂。

3 仿真結果與分析

本節提出在VHTS多播場景下將和吞吐量最大化問題轉換為加權均方誤差最小化問題(以下稱為本文算法)求解,在本節對本文算法進行性能仿真并與文獻[8]中的應用MMSE的算法進行性能對比分析,兩者的計算復雜度均為多項式級復雜度。為保證仿真結果的準確性,2種算法均在同一個場景下進行仿真比較,具體參數如表1所示。

波束的吞吐量是算法性能的重要指標之一,2種算法的性能分別如圖3和圖4所示。圖3表示每幀內調度用戶數K為6時2種算法的波束吞吐量,圖4表示每幀內調度的用戶數K不同時2種算法的平均每個波束的吞吐量。

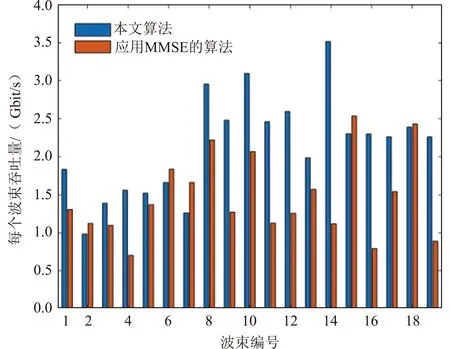
圖3 K為6時每個波束的吞吐量Fig.3 Throughput of each beam for K=6

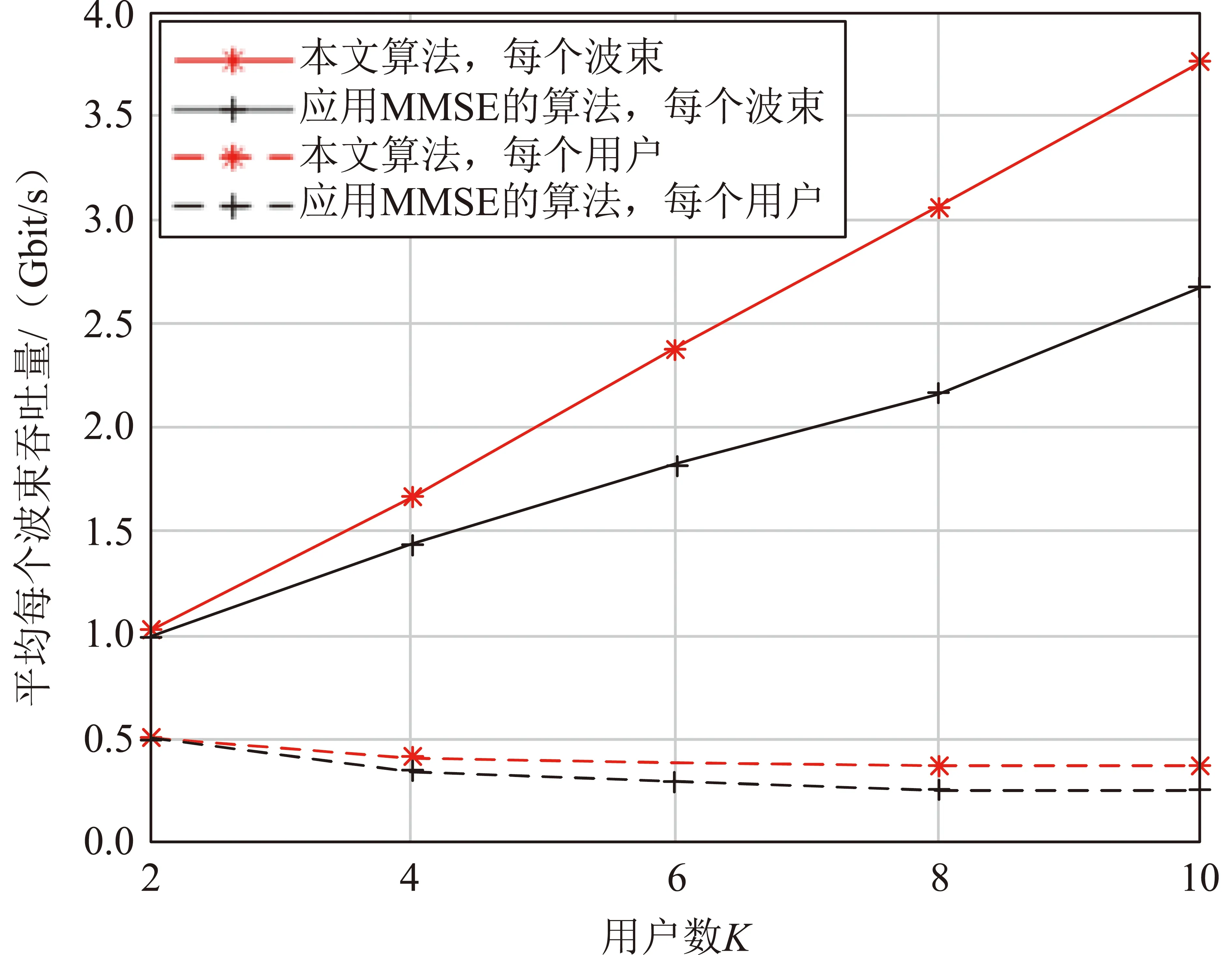
圖4 平均每個波束的吞吐量Fig.4 Average throughput of each beam

由圖3可知:當K為6時,本文算法的平均每個波束吞吐量為2.1485Gbit/s,而應用MMSE的算法的平均每個波束吞吐量為1.4717Gbit/s,前者比后者提升了46.0%,表明本文算法明顯優于應用MMSE的算法,優勢更突出。

圖4表示每個波束調度的用戶數對系統性能的影響,其中,實線表示用戶數K取不同值時平均每個波束的吞吐量,虛線表示平均到每個用戶的吞吐量。可以看出:隨著調度的用戶數K的增加,2個算法的每個波束吞吐量都在隨之提升,但是平均每個用戶的吞吐量隨著調度的用戶數的增加而降低。這是因為:隨著調度的用戶數增加,用戶信道的差異性逐漸增大,針對最差用戶信道進行的線性預編碼設計會導致其他用戶的性能損失越來越大,使得平均每個用戶的吞吐量下降,但波束內調度的用戶數還在增加,波束內總的吞吐量也在提升。

從圖4中還可以看出:相比于應用MMSE的算法,本文算法在波束吞吐量上有明顯的提升,通過迭代MMSE接收機、加權值及最小化加權MSE的方式優化線性預編碼。其中:加權值為上一次迭代得到的MSE的倒數,這使得經過優化預編碼后波束間吞吐量差異較小,系統整體的吞吐量提升。當用戶數較少時,極端情況為單播場景,本文算法退化為加權MSE最小化算法,波束間的加權值較小,使得波束間功率平均分配,系統性能較差;隨著用戶數的增加,系統權重值依據多個用戶的MSE來選擇,迭代后不同波束之間的權重值有一定的差異,使得本文算法的平均每個波束吞吐量優于應用MMSE的算法。

圖5為每幀內調度用戶數K為6時,本文算法與應用MMSE的算法的平均每個波束吞吐量與星上總功率的關系曲線。可以看出:隨著功率的增加,平均每個波束吞吐量近似與功率呈對數關系。在考慮的功率范圍內,本文算法相比于應用MMSE的算法始終有25%以上的頻譜效率提升。在較低功率范圍內,本文算法的性能增益更顯著,因此可以適應不同的功率條件,在考慮的功率范圍內都能表現出更優的性能,且在功率較低時對頻譜效率的提升作用更為明顯。

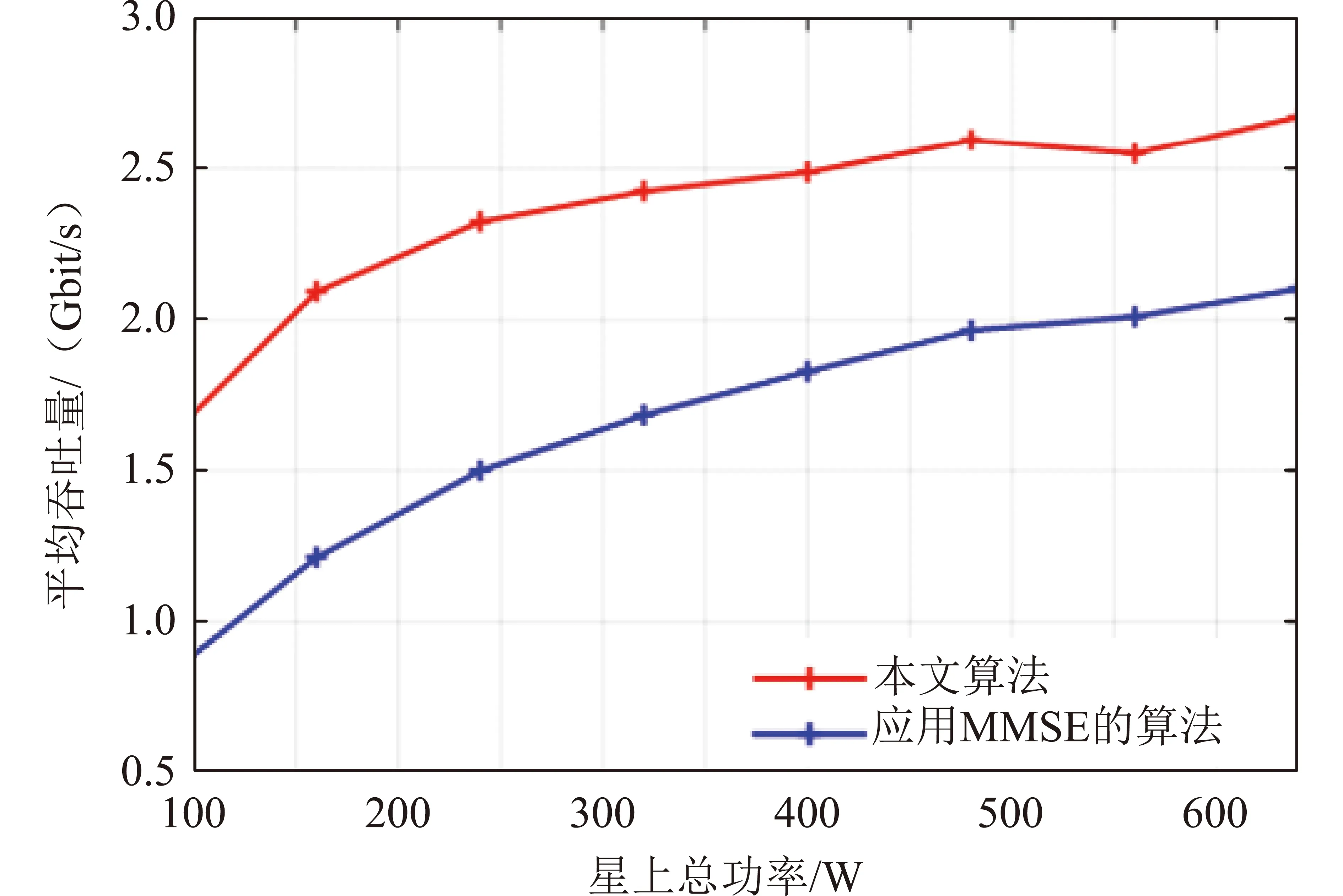
圖5 平均每個波束吞吐量隨星上總功率的變化Fig.5 Average throughput of each beam with different sum power

4 結束語

本文設計了VHTS通信系統多播場景下的線性預編碼算法。考慮星上天線的功率約束,以最大化系統總吞吐量為目標,將最大化和吞吐量問題轉換成與接收機聯合設計的加權和均方誤差最小化問題求解,并采用ADMM將加權均方誤差最小化問題分解為多個并行求解子問題,得到每個變量更新的閉式解。仿真結果表明:本文算法與應用MMSE的算法相比,在不同功率和不同每幀用戶數條件下都能實現顯著的頻譜效率增益,同時計算復雜度較低,可應用于后續全頻率復用VHTS通信系統。