低軌導航增強衛星廣播星歷擬合模型研究

楊開偉 劉涵宇 孫騰達 孫秀聰 徐明

(1 中國電子科技集團公司第五十四研究所,石家莊 050081)(2 北京航空航天大學宇航學院,北京 102206)

近年來,全球衛星導航系統(GNSS)迅速發展,在人類社會生活的方方面面發揮著不可或缺的作用,涉及到測繪、交通、救援等諸多方面。隨著自動駕駛、物聯網、5G等新興產業的發展,社會生產生活對衛星導航服務提出了更高的要求,對時空信息的需求發展為精準、實時、動態和全球[1-2]。GNSS的不足之處也逐漸顯露出來。GNSS在常規情況下只能提供10m左右的定位精度,而無法滿足用戶高精度的需求;此外,導航衛星信號到達地面時極其微弱,不但導致其極易受到干擾和欺騙,而且導致其難以穿透物理遮蔽,無法在室內、水下等復雜地形中提供高精度的定位服務[1,3-4]。

導航增強技術是解決上述問題、提升導航服務性能的一種可行方案,能利用低軌導航增強衛星產生測距信號并與中高軌GNSS系統協同提供導航服務[5]。傳統的導航增強系統采用的是地球靜止軌道(GEO)衛星,但GEO衛星軌道資源有限,而且用戶接收到的信號弱,容易受到干擾,無法滿足用戶日益增長的高精度定位需求[6]。低軌衛星則沒有上述問題,其軌道高度低,信號的自由空間損耗低,落地信號更強,抗干擾性能更好。此外,由于低軌導航增強衛星的飛行速度較快,相等時間的位置變化較大,從而使得歷元間量測信息的相關性下降,能提高系統的可觀測度,加快載波相位模糊度的收斂速度[4]。例如,美國的銥下一代(Iridium NEXT)星座提供的衛星授時與定位服務,已經能夠脫離GPS單獨提供定位服務,因而低軌導航增強衛星可以在GPS受到干擾的情況下提供備份的導航服務[4]。我國的珞珈一號衛星搭載有導航增強載荷,并開展了一系列低軌衛星增強相關試驗[7]。

高精度確定用戶的位置需要導航衛星高精度的位置信息,導航衛星的位置信息由廣播星歷計算,因此廣播星歷的高精度計算方法得到了廣泛的研究。目前,應用廣泛的廣播星歷參數模型有2種,主要是針對中高軌衛星,一種是以GPS為代表的基于軌道根數的廣播星歷參數模型;一種是以格洛納斯(GLONASS)為代表的基于軌道狀態的廣播星歷參數模型[8]。GPS廣播星歷參數模型的精度和GLONASS相當,但前者的預報能力更強,用戶算法更簡單;后者的優勢是其參數更少,占用導航信號的資源少。衛星設備、通信鏈路和用戶性能等多方面的限制,要求廣播星歷模型具有參數少、外推能力強、用戶算法簡單等特點,因此GPS廣播星歷參數模型應用更加廣泛[9]。

傳統的GPS系統采用的是包括6個開普勒軌道參數、3個軌道參數變化項、6個調和項系數和1個參考歷元的16參數模型[10]。在原來16參數的基礎上,GPS系統后續又發展了18參數模型。18參數模型中考慮衛星所受攝動力對衛星軌道半長軸、平均角速度及升交點赤經的影響,相較于16參數模型更加注重衛星軌道的瞬時變化,擬合精度更高[11]。16參數模型和18參數模型都是針對中高軌衛星設計的,而低軌衛星與中高軌衛星所受攝動力有所區別,如果將這種參數模型直接應用在低軌衛星上,將無法滿足高精度的定位需求[12],因此需要根據低軌衛星的特點重新設計廣播星歷參數模型。文獻[12]中利用軌道高度約1000km的低軌衛星在16參數模型的基礎上設計了26參數的廣播星歷擬合算法,增加了軌道偏心率的變化率、升交角線性變化率和8個調和改正項振幅共10個參數,其2h軌道弧段的均方差小于10m,局部弧段擬合誤差小于25m,但參數過多,因此占用的導航信號資源多。文獻[6]中考慮了低軌衛星攝動力的短期變化快,在GLONASS廣播星歷參數模型的基礎上設計了基于軌道狀態的22參數模型。其研究顯示:當低軌衛星軌道高度大于700km時,用戶距離誤差(FURE)精度在5cm以內;當軌道高度降低至500km時,FURE精度優于0.1m。雖然相對于26參數模型來說22參數模型參數少,但是用于確定衛星位置的用戶算法外推效率較低,因此限制了其被廣泛應用。針對26參數和22參數占用導航信號資源多、用戶算法復雜的問題,本文提出了一種兼具擬合精度、計算效率和占用導航信號資源少的模型。考慮到大氣阻力主要改變平面內的軌道要素,在18參數模型的基礎上僅增加偏心率變化率這一參數,設計了19參數模型,并針對500～2000km高度的低軌衛星進行了19參數模型最小二乘擬合,檢驗了這種星歷模型的有效性,驗證了其擬合精度要優于18參數模型。本文提出的19參數模型對大傾角(不小于30°)衛星的長時弧段(4h)的位置擬合精度與26參數模型近似,但所需參數量大大減少,可為低軌導航增強衛星的廣播星歷提供一種兼顧精度與計算資源的模型。

1 19參數模型

1.1 廣播星歷參數

18參數模型采用軌道根數加攝動參數的形式表示,包括6個開普勒軌道參數、5個軌道根數變化項、6個調和項系數和1個參考歷元。19參數模型在18參數模型的基礎上添加偏心率變化率這一參數。表1給出了參考歷元toe時刻19參數廣播星歷的符號說明。

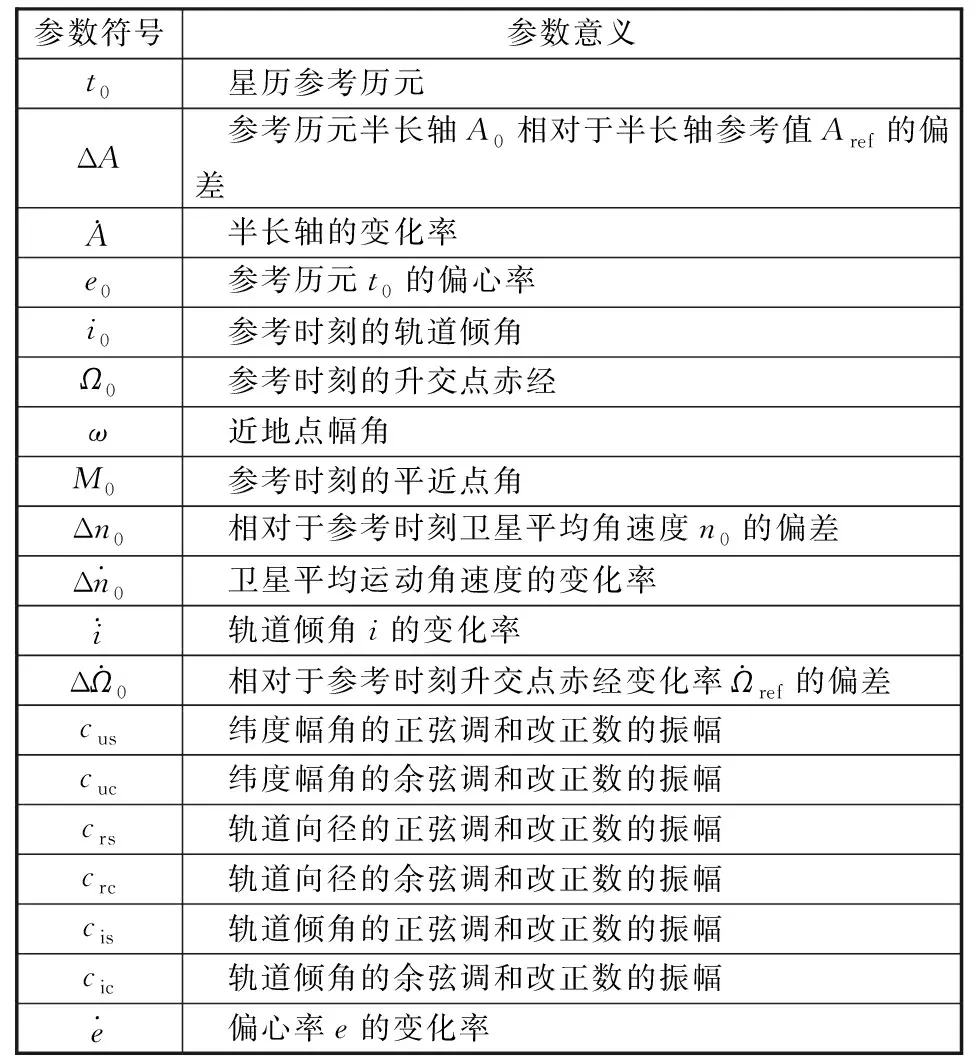
表1 19參數廣播星歷參數定義Table 1 19-parameter broadcast ephemeris parameter definition

1.2 19參數廣播星歷用戶算法

用戶算法是指用戶使用廣播星歷計算衛星位置的公式。在短時間內,使用廣播星歷可以較精確地描述衛星的位置。在之后的一段時間里,廣播星歷仍能描述衛星的位置,只是誤差會隨著外推時間變長而增大。對于一般軌道,19參數廣播星歷用戶算法如下。

1)計算觀測歷元t到參考歷元t0的時間差tk

tk=t-t0

(1)

式中:k為第k時刻。

2)計算觀測歷元半長軸A

(2)

3)計算衛星平均角速度

(3)

式中:μ為地心引力常數;Δn為觀測歷元相比參考歷元的衛星平均角速度變化量;n為觀測歷元衛星平均角速度。

4)計算觀測瞬間的平近點角Mk

Mk=M0+ntk

(4)

5)計算偏心率e

(5)

6)迭代計算偏近點角Ek

Ek=Mk+esinEk

(6)

7)計算真近點角Vk

(7)

8)計算攝動改正前的緯度輻角Φk

Φk=Vk+ω

(8)

9)計算攝動改正后的緯度輻角uk、衛星矢量半徑rk和軌道傾角ik的攝動改正項δuk,δrk,δik

(9)

10)計算經過攝動改正的uk,rk,ik

(10)

11)計算衛星在軌道平面上的位置(xk,yk)

(11)

12)計算觀測時刻的升交點經度(格林威治子午圈到衛星軌道升交點)

(12)

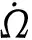
13)計算衛星在地心固連坐標系中的位置(X,Y,Z)

(13)

當直接利用常規的軌道根數方法對軌道傾角近似為0°的衛星進行廣播星歷參數擬合時,會導致法方程系數矩陣成為病態矩陣,使方程組的解誤差變大,進而造成擬合精度降低。因此,為了解決小軌道傾角造成的衛星廣播星歷擬合精度降低甚至擬合失敗的問題,本文采用軌道旋轉法[11],先將地心慣性坐標系繞X軸(由地心指向春分點)旋轉一個角度,在新坐標系計算廣播星歷,在用戶預測衛星位置時將慣性坐標系旋轉相反的角度,得到位置矢量在原慣性坐標系下的表達,進一步得到地心固連坐標系下的位置矢量。對于軌道傾角近似為0°的情況,坐標轉換的過程見圖1。

2 19參數廣播星歷擬合算法

19參數廣播星歷擬合算法流程如圖2所示。首先,輸入被擬合衛星一段時間的精密位置和初始時刻的精密速度,設置擬合時長,并對小傾角情況進行坐標系旋轉。然后,設計19參數的迭代初值,除軌道六要素對應的參數外其他參數置為零。最后,利用最小二乘擬合算法迭代計算19參數,直至迭代改正量足夠小時停止。其中,當傾角不大于ε時,認為屬于小傾角情況,需要進行坐標系旋轉,本文取ε為1°。通過判斷改正量的模是否足夠小(可以取閾值為1×10-2)或已經達到最大迭代次數(可以取10000次)作為迭代終止條件。下面對擬合算法進行詳細介紹。

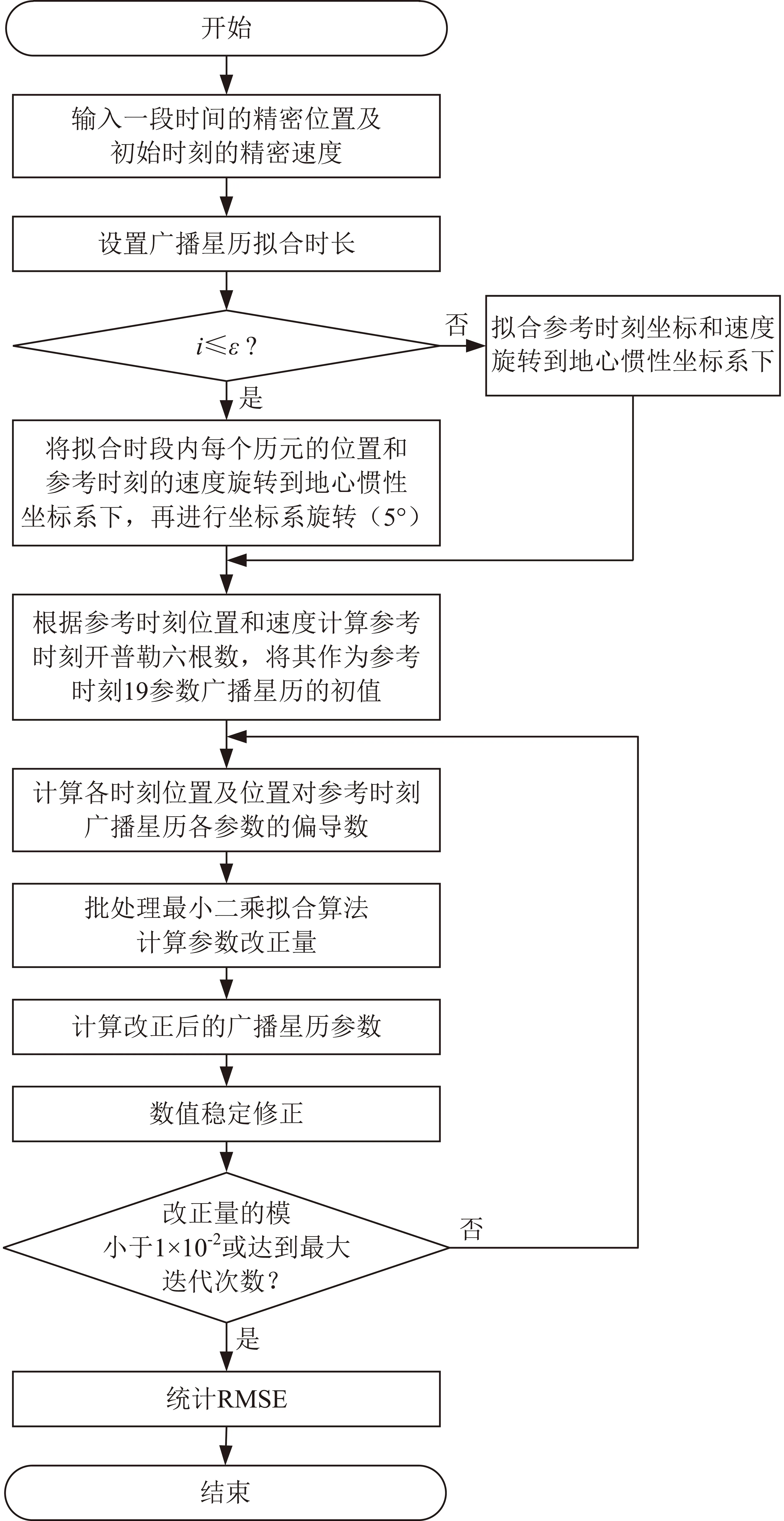
圖2 廣播星歷擬合算法流程Fig.2 Broadcast ephemeris fitting algorithm flow

2.1 最小二乘擬合算法

廣播星歷參數的設計是實現高精度擬合的前提條件,而擬合算法的設計則是擬合精度和穩定性的重要保證。擬合算法的核心內容是參數估計,經典的參數估計法有最小二乘估計、極大似然估計、極大驗后估計、貝葉斯估計等。其中,經典的最小二乘估計法是比較簡單且容易理解的估計方法,在參數模型合理、觀測值誤差較小的情況下,采用最小二乘擬合算法就可以保證較高的擬合精度。

批處理最小二乘擬合算法的基本原理為是結合動力學模型與觀測模型對狀態量進行迭代平差,使得給定時間段內測量估計值與實際測量值之差的平方和最小。

對于一個非線性系統,有

z=h(x)+ν

(14)

式中:z為低軌衛星的精確位置信息;x為19參數廣播星歷;h(x)為通過用戶算法計算出的低軌衛星的位置信息;ν為精確位置和計算位置的誤差。

最小二乘擬合算法是使殘差的平方和最小,即讓評價函數J最小。

J=(z-h(x))T(z-h(x))

(15)

由于最小二乘擬合算法只能用于線性系統,因此需要對系統線性化,在x0處線性化后的殘差可以表示為

Δz-HΔx0

(16)

可以使用線性最小二乘擬合算法求解式(14),得到

Δx0=(HTH)-1(HTΔz)

(17)

進而,原問題的最小二乘解為x=x0+Δx0。在線性化過程中舍棄了系統二階及以上的信息,所以不可避免地引入誤差,造成精度損失,即所得到的估計值并不是原問題的最優估計值。因此,還需要以所得估計值作為新的初值,重新迭代計算,直到算法收斂,即可得到狀態量的最優估計值。

(18)

式中:rk為第k時刻的衛星位置;?rk/?e由文獻[11]給出。

2.2 數值穩定修正

數值穩定修正是為了確保擬合算法能得到正確的結果,下面對修正方法進行具體介紹。

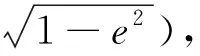
(2)升交點赤經、近地點幅角、平近點角。為保證數值穩定性,需要在每次迭代施加改正量之后對升交點赤經、近地點幅角、平近點角進行歸一化,也就是讓其落在[0,2π],之后再繼續進行下一次迭代。例如,當Mk過大時,可能會因為數值問題無法通過迭代求出Ek。

(3)解線性方程組。最小二乘擬合算法問題需要求解線性方程組(HTH)Δx0=HTΔz,但HTH條件數很小,甚至接近病態,直接求逆或者直接使用高斯消元法求解誤差較大。因此,本文使用下三角上三角(LU)分解法求解線性方程組。LU分解法可以將1個矩陣分解為1個下三角矩陣和1個上三角矩陣的乘積。如果使用杜利特爾(Doolittle)分解,得到的下三角矩陣為單位下三角矩陣;如果使用克勞特(Crout)分解,得到的上三角矩陣為單位上三角矩陣。首先,對(HTH)Δx0=HTΔz中的HTH進行LU分解,即LU=HTH,則(HTH)Δx0=HTΔz則可以寫為LUΔx0=HTΔz,令y=UΔx0,可以先解線性方程組Ly=HTΔz,得到y,再解線性方程組y=UΔx0,得到Δx0,從而相比于直接解線性方程組能夠降低系數矩陣的病態程度,誤差更小。

3 仿真結果及分析

本文使用高精度軌道預報器預報的衛星位置作為精密星歷,高精度軌道預報器中非球形引力攝動考慮70階70次全球超高階地球重力場模型(EGM2008),大氣阻力模型使用質譜儀非相關散射模型(NRLMSISE-00),同時考慮日月三體引力;參考時刻為2010-09-19T04:00(UTC),參考時刻的偏心率取0,升交點赤經、近地點幅角和平近點角均取0°。

下面對不同軌道高度(500km,1000km,1500km,2000km)及不同軌道傾角(0°,30°,60°,90°)的軌道進行19參數廣播星歷最小二乘擬合。設置擬合初值如下。參考時刻半長軸取為參考時刻衛星的半長軸,參考時刻升交點赤經變化率取為0,19參數中的參考時刻、偏心率、升交點赤經、近地點幅角和平近點角按照衛星參考時刻的實際數據設置,其余參數設為0。衛星位置采樣時間間隔為1min,即每分鐘獲取1組位置,擬合時長分別考慮20min,30min,60min,2h,3h,4h的情況。

繪制上述仿真場景下的位置均方根誤差(RMSE),計算公式為

(19)

式中:Δx,Δy,Δz為地心固連坐標系下的位置誤差。

表2～5中給出了18參數和19參數模型擬合的RMSE曲線對各個時刻的均方根,圖3～6中給出了同一軌道傾角、同一擬合時長時不同軌道高度對擬合效果的影響。

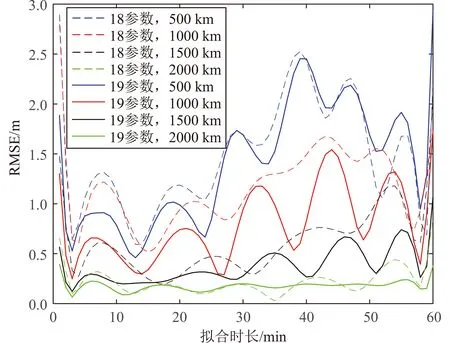
圖3 軌道傾角0°、擬合時長60min時不同軌道高度對18參數和19參數模型的擬合效果Fig.3 Fitting results of different orbit altitudes on 18-parameter and 19-parameter models when inclination angle is 0° and fitting time is 60 minutes

表2 軌道傾角為0°時不同軌道高度擬合結果的RMSETable 2 RMSEs of fitting results for different orbit altitudes at an inclination angle of 0° m

從表2和圖3可以看出:對于任何擬合時長,擬合RMSE隨軌道高度的升高而減小,原因是軌道高度越高,同等時間下軌道的非線性越弱,最小二乘法更能發揮優勢;同時,隨著軌道高度的升高及非球形引力攝動和大氣阻力攝動的下降,軌道更接近二體軌道,因此擬合誤差會有所下降。19參數模型擬合時長為20min時精度達到厘米級,30min時精度達到分米級,60min時精度達到米級。隨著擬合時間的增長,RMSE有所增大,這是因為軌道根數預報是基于二體模型的,即使廣播星歷增加了攝動修正項,但其只有6個系數,遠遠不足以描述全部的攝動力,因此也只能解決短時間內的擬合問題,隨著時間增長,誤差仍然會越來越大。總體上來說,19參數模型的擬合精度要高于18參數模型。

從表3和圖4可以看出:軌道傾角為30°時同樣可以得到與軌道傾角為0°時相同的結論,即對于任何擬合時長,擬合RMSE隨軌道高度升高而減小,整體上19參數模型的精度要高于18參數模型。對比軌道傾角為30°和0°的2種場景,可以發現:當軌道高度和擬合時長相等時,30°軌道的擬合誤差略大于0°軌道的擬合誤差。

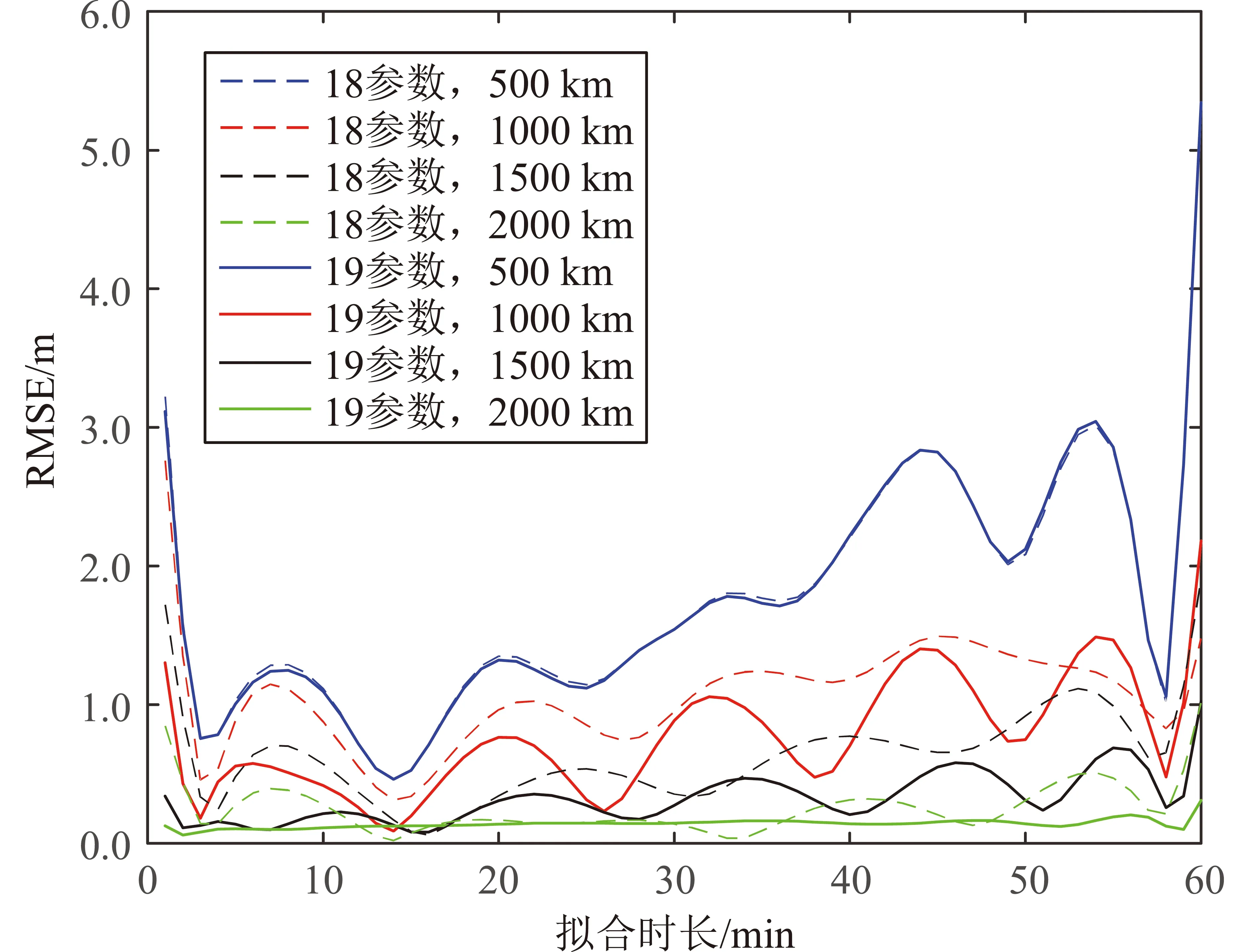
圖4 軌道傾角30°、擬合時長60min時不同軌道高度對18參數和19參數模型的擬合效果Fig.4 Fitting results of different orbit altitudes on 18-parameter and 19-parameter models when inclination angle is 30° and fitting time is 60 minutes

表3 軌道傾角為30°時不同軌道高度擬合結果的RMSETable 3 RMSEs of fitting results for different orbit altitudes at an inclination angle of 30° m

從表4和圖5可以看出:軌道傾角為60°時同樣可以得到與軌道傾角為0°和30°時相同的結論。軌道傾角60°時的擬合誤差大于軌道傾角0°時的擬合誤差,與30°傾角時近似。

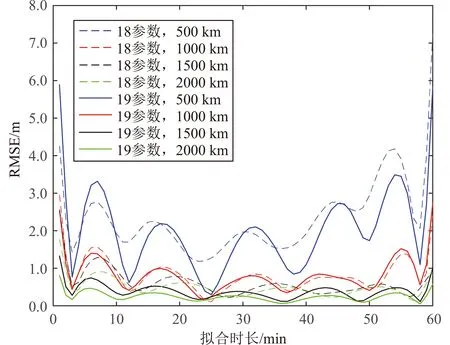
圖5 軌道傾角60°、擬合時長60min時不同軌道高度對18參數和19參數模型的擬合效果Fig.5 Fitting results of different orbit altitudes on 18-parameter and 19-parameter models when inclination angle is 60° and fitting time is 60 minutes

表4 軌道傾角為60°時不同軌道高度擬合結果的RMSETable 4 RMSEs of fitting results for different orbit altitudes at an inclination angle of 60° m

從表5和圖6可以看出:軌道傾角為90°時同樣可以得到與軌道傾角為0°、30°和60°時相同的結論。

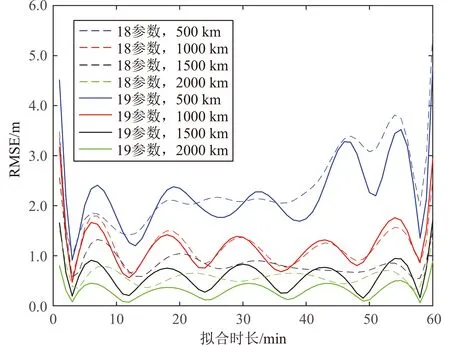
圖6 軌道傾角90°、擬合時長60min時不同軌道高度對18參數和19參數模型的擬合效果Fig.6 Fitting results of different orbit altitude on 18-parameter and 19-parameter models when inclination angle is 90° and fitting time is 60 minutes

表5 軌道傾角為90°時不同軌道高度擬合結果RMSETable 5 RMSEs of fitting results for different orbit altitudes at an inclination angle of 90° m

總的來看,19參數模型對不同軌道高度(500～1000km)、不同軌道傾角的衛星在不同擬合弧段時長下的擬合均具有很好的適用性;同時,19參數模型的精度要高于18參數模型。

進一步對比19參數模型和26參數模型的長弧段(4h)位置擬合精度,結果如表6所示。從表6可以看出:當軌道傾角不小于30°時,在12種不同軌道高度和傾角的情況中,有8種情況是19參數模型精度更高,另外4種情況是26參數模型精度更高。這證明了增加軌道傾角變化率這一參數對長弧段擬合精度的提升是有顯著幫助的,使得19參數模型對于大傾角衛星的長弧段擬合達到了與26參數模型近似的精度。同時,26參數模型在有些情況下擬合精度低于18參數模型,這是因為26參數模型是由16參數模型發展而來的,其沒有考慮18參數模型相較16參數模型增加的軌道高度變化率和角速度變化率。

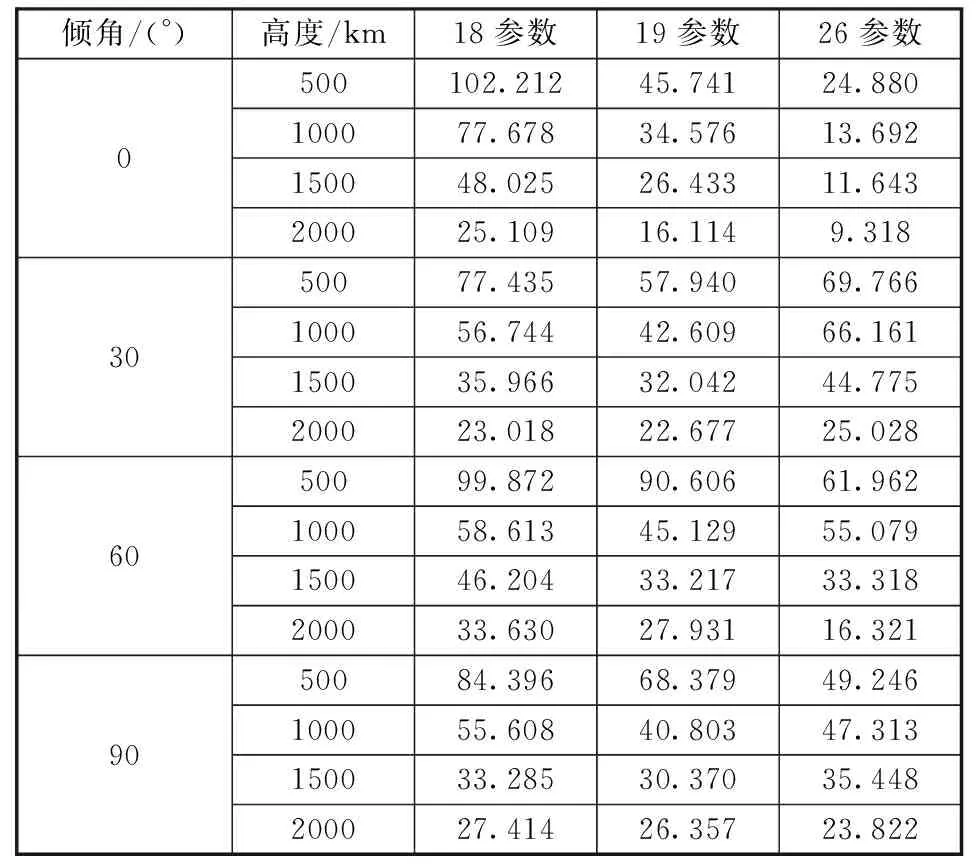
表6 不同軌道高度、不同傾角的4h擬合結果RMSETable 6 RMSEs of fitting results for different orbit altitudes and inclination angles when fitting time is 4 hours m

本文在GPS的18參數模型基礎上增加了偏心率變化率這一參數,仿真結果證明這一參數對于提高低軌導航增強衛星的位置擬合精度具有重要作用。如何在本文提出的19參數模型基礎上,在不增加過多參數前提下進一步提高位置擬合精度,值得進一步研究。表6為此提供了重要方向,即:對于小傾角(0°)衛星的長弧段擬合,26參數模型的位置擬合精度遠高于19參數模型;而對于大傾角(不小于30°)衛星,二者精度則近似。因此,導致26參數模型對小傾角衛星的位置擬合精度較高的主要參數十分值得研究,進而可以將這些起主要作用的參數與19參數模型結合,以提高后者對于小傾角衛星的位置擬合精度。

4 結論

本文針對軌道高度為500～2000km的低軌衛星,在GPS的18參數模型基礎上僅增加偏心率變化率這一參數,設計了19參數模型,并與18參數模型的精度進行了比較,試驗分析結論如下。

(1)對于軌道高度為500～2000km的低軌衛星,采用19參數模型擬合精度高。

(2)隨著低軌衛星軌道高度的降低,19參數模型的擬合精度降低,這是因為軌道高度越低,大氣阻力的影響越顯著,導致擬合精度降低。

(3)總體來說,在相同軌道高度、軌道傾角和擬合時長的條件下,19參數模型的擬合精度要高于GPS的18參數模型。

此外,本文通過仿真驗證了19參數模型對于大軌道傾角衛星的長弧段位置擬合精度與26參數模型近似,但所需參數量大大減少,因此可以提高計算效率和減少存儲資源的需求。因此,本文的研究為低軌導航增強衛星的廣播星歷提供了一種兼顧精度高與資源需求少的模型。