河段挾沙力計算方法及其在黃河下游的應用

夏軍強，戈向陽，周美蓉

（1.武漢大學水資源工程與調度全國重點實驗室，湖北武漢 430072；2.水利部牧區水利科學研究所，內蒙古呼和浩特 010020）

0 引言

小浪底水庫蓄水攔沙運用改變了黃河下游的徑流過程，清水下泄使得下游發生劇烈的沖刷［1-2］，河道斷面形態趨向窄深［3-4］，對黃河下游水流挾沙力及河道輸沙能力產生了很大影響。 研究黃河下游近期水流挾沙力的時空變化特點，對于確定黃河下游河槽排洪輸沙基本功能和水沙調控指標具有重要意義。

水流挾沙力作為泥沙基本理論研究的一個傳統課題，是指河道沖淤平衡狀態下單位水流挾帶泥沙的能力，其變化是研究懸沙輸移及河道演變的核心問題之一。 國外最早關于水流挾沙力的研究始于Gilbert等［5］的水槽輸沙試驗；我國水流挾沙力研究于1947年［6］開始，1954 年南京水利實驗處進行了人工沙飽和懸沙試驗，并根據試驗數據得到水流挾沙力經驗關系式［7］。 截至目前，國內外學者關于水流挾沙力已提出大量經驗半經驗公式，其中具有代表性的有Einstein公式［8］、張瑞瑾公式［9］、Bagnold 公式［10］、竇國仁公式［11］、張紅武公式［12］、韓其為公式［13］等。 其中，張紅武等［12］認為泥沙懸浮能量來自水流運動動能、水流能量消耗和泥沙懸浮功，且這三者之間必定存在著內在聯系，并考慮到卡門常數和泥沙沉速等會受泥沙存在的影響，提出了一個半經驗半理論的水流挾沙力公式（業內稱為張紅武公式）。 大量研究證明張紅武公式在計算高含沙水流挾沙力時具有較高精度［14-15］。 然而目前水流挾沙力公式大多只能計算典型斷面的挾沙力，用于反映整個河段的情況［16-18］。 如：劉繼祥［16］選取黃河中下游干支流14 個水文站，研究了黃河下游的水流挾沙力及其影響因素；要威等［17］基于黃河下游游蕩段花園口—高村河段的水沙資料，得出了適用于斷面形態變幅大的游蕩段的挾沙力沿河寬分布的公式；Xia 等［18］根據黃河下游8 個水文站的實測挾沙力資料，驗證了張紅武公式中參數取值的準確性。 但特定斷面的水流挾沙力調整情況無法代表整個河段。

因此，本文基于實測水沙和地形資料，提出了一種河段水流挾沙力的計算方法，分析了1986—2020 年黃河下游游蕩段、過渡段、彎曲段河段挾沙力的時空變化特點。

1 河段挾沙力的定義及計算方法

1.1 河段挾沙力定義

黃河下游河床形態沿程變化劇烈，實測水文斷面分布不均，河段內某一特定斷面的挾沙力難以代表整個河段的挾沙能力。 因此，需要結合河段尺度的河床形態參數，提出河段挾沙力的計算方法。 首先進行河道概化，綜合考慮河段內各個斷面的形態和流量，以及相鄰斷面間距不等的實際情況，提出一個理想的河段平均化的斷面（見圖1，圖中Q、S、A、H分別為流量、含沙量、斷面面積、水深）。 然后提出河段挾沙力的定義：在河段平均的水流和泥沙綜合條件下，能夠通過河段下泄的臨界含沙量。 當水流中含沙量超過這一數值時，河段將發生河床淤積；反之，河段將發生河床沖刷。

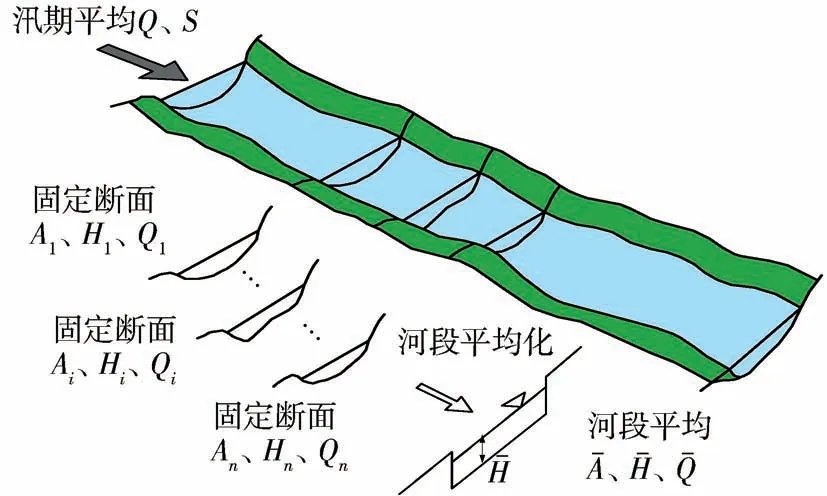
圖1 河道概化

1.2 河段挾沙力計算方法

張紅武公式應用廣泛，在計算高含沙水流和低含沙水流的挾沙力時均具有較高的精度，因此本文將其作為推導河段平均挾沙力的基礎公式，具體形式如下［12］：

式中：U為流速，H為水深，g為重力加速度，ωm為非均勻懸沙的平均沉速，Sv為體積比含沙量，γs和γm分別為泥沙容重和渾水容重，κ為渾水的卡門常數，D50為床沙的中值粒徑，k為系數，m為指數。

選定了挾沙力公式后，要對公式中的參數進行河段平均化處理，主要包括河道水力幾何參數的河段平均化以及泥沙參數的計算。

1.2.1水力幾何參數的河段平均化

河段平均流量與過水斷面面積采用Xia 等［19］提出的基于對數變換的幾何平均與斷面間距加權平均結合的方法來計算，可保證河道形態的連續性，即存在為平均河寬，為平均水深）。 具體步驟如下：首先采用一維水沙數學模型［20］計算出各統測斷面不同流量對應的水位；然后根據各斷面的水位流量關系，確定汛期平均流量對應的水位，從而計算出相應的過水斷面面積、河寬、水深；最后采用式（3）計算河段平均值。

1.2.2泥沙參數計算

水流挾沙力公式中需要平均化的泥沙參數包括Sv、γm、ωm等。 其中體積比含沙量的轉換公式為Sv＝S／ρs（S為含沙量，ρs為泥沙的天然密度，取2 650 kg／m3），渾水容重的計算式為γm＝ρmg＝［ρ水（1-Sv）+ρ沙Sv］g，渾水的卡門常數與清水的卡門常數κ0＝0.4 的關系為本文采用河段內各水文斷面泥沙參數的算術平均值作為河段平均的泥沙參數值。 此外，非均勻懸沙平均沉速（ωm）采用韓其為［21］方法計算：

式中：N為挾沙力分組數；pi為挾沙力級配，可以用李義天［22］方法確定；n為待確定量，根據以往研究成果取為第i粒徑組泥沙的群體沉速，其中d50為懸沙中值粒徑，ωi為第i粒徑組泥沙在清水中的沉速，這里采用張瑞瑾泥沙沉速公式［9］進行計算。

通常認為黃河下游懸沙粒徑小于0.025 mm 的細沙為沖瀉質，不參與造床作用，故計算懸沙平均沉速時不考慮沖瀉質組分。

1.2.3挾沙力公式參數率定

經過水力幾何參數的河段平均化以及泥沙參數計算，張紅武公式可轉換為如下形式：

定義水沙綜合參數：

將河段平均水力幾何參數與泥沙參數代入后即可得到黃河下游各河段1986—2020 年逐年的水沙綜合參數，如圖2 所示。 游蕩段水沙綜合參數的取值為0.07～49.66，小浪底水庫運用前多年平均值為28.27，小浪底水庫運用后減小至1.46；過渡段水沙綜合參數的取值為0.12 ～68.48，多年平均值由小浪底水庫運用前的32.62 減小至小浪底水庫運用后的2.38；彎曲段水沙綜合參數的取值為0.14 ～63.59，多年平均值由小浪底水庫運用前的27.45 減小至小浪底水庫運用后的2.73。

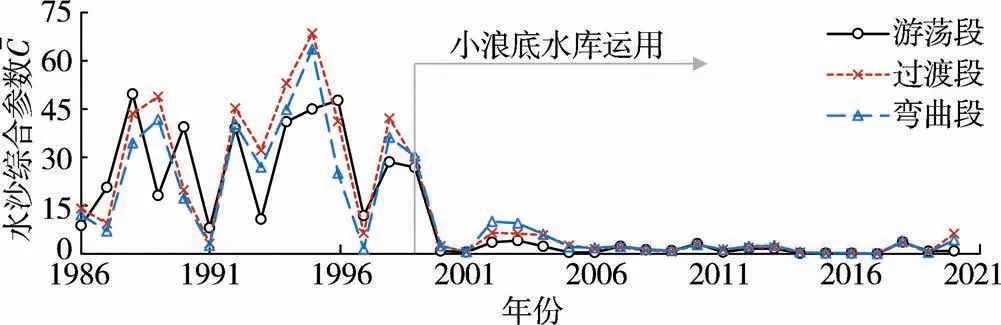
圖2 黃河下游各河段水沙綜合參數逐年變化情況

張瑞瑾［9］的研究結果表明，挾沙力公式的系數k和指數m隨水沙綜合參數變化而變化。 當公式中的水沙參數拓展到河段平均的形式后，有必要重新率定張紅武公式中的系數k和指數m，使之更準確地反映河段水沙條件下的水流挾沙力。 本文從一維河流數學模型基本控制方程組中的河床變形方程入手，通過年度實測沖淤量倒推計算河段挾沙力；接著擬合各河段水沙綜合參數與挾沙力計算值的冪函數關系，即可得到河段挾沙力公式中的系數k和指數m。河床變形方程：

經過公式變換得到S*的表達式為

式中：A0為河床總沖淤斷面面積，t為時間，ρ'為床沙干密度，ωm為懸沙沉速，α為恢復飽和系數（采用韓其為［23］在研究非均勻懸移質不平衡輸沙時提出的方法，當河床淤積時α＝0.25，河床沖刷時α＝1.0）。

2 黃河下游河段挾沙力計算結果

2.1 研究河段概況

研究河段干流全長756 km，總落差94 m，流域面積2.3 萬km2，占黃河總流域面積的3%。 河段內大量泥沙落淤，部分河段形成了舉世聞名的地上“懸河”。黃河下游按照河道形態及河床演變特點可分為游蕩段、過渡段、彎曲段［24］，如圖3 所示，沿程有花園口、夾河灘、高村等7 個水文站。 總體來說，黃河下游河道具有上寬下窄、上陡下緩、上段沖淤變化大、下段較為穩定等特點。 游蕩段全長299 km，河道比較順直，具有水流寬淺散亂、主流擺動不定、河勢變化劇烈等演變特點。 過渡段長約185 km，該河段區間無支流入匯，平灘河槽相對較窄，河段內有大量河道整治工程，河勢基本得到控制。 彎曲段長約272 km，沿岸設有大量的險工和控導工程，防護長度占該河段總長的70%以上［25］，主槽形態較為窄深，灘槽高差較大。

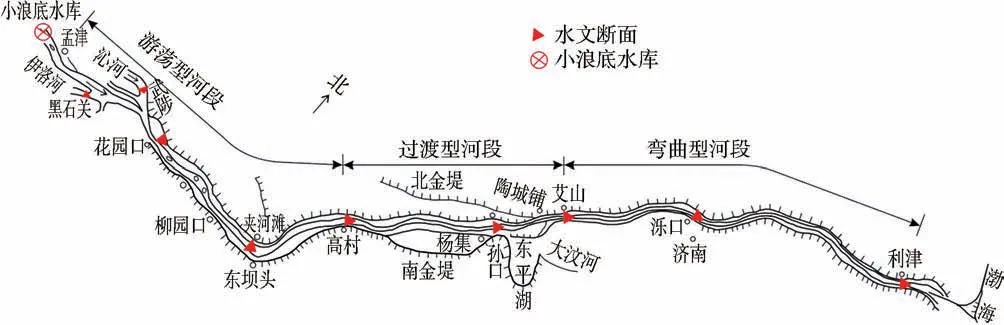
圖3 黃河下游河道示意

黃河下游的水沙來源主要是三門峽以上干流、三門峽至花園口區間。 圖4（a）點繪了1986—2020 年進入黃河下游的水沙變化過程。 小浪底水庫運用前（1986—1999 年）黃河下游的年均水量為279 億m3，年均沙量為6.9 億t。 小浪底水庫運用后，受中上游水土保持、水庫蓄水攔沙、水沙聯合調度等因素影響，黃河下游年均水量為277 億m3，年均沙量顯著減小至1.0億t，較1986—1999 年減小了85%。 此外，來水量年內分配發生變化，非汛期來水量占比增大，1986—1999 年非汛期來水量占全年的53%，而2000—2020年提升至60%；來沙量大幅度減少，2000—2020 年年均來沙量僅為1986—1999 年的15%，且來沙集中在汛期，占全年的80%。

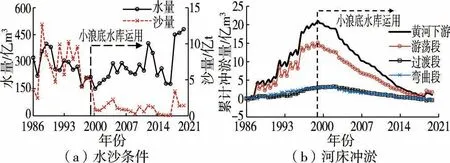
圖4 黃河下游水沙條件及累計沖淤量變化情況

小浪底水庫運用前，進入黃河下游的水少沙多，水沙關系嚴重不協調，河床長期處于淤積狀態，但是在一些有利的水沙條件下，也會出現河床沖刷［26］；小浪底水庫運用后，黃河下游處于持續沖刷狀態。 圖4（b）為黃河下游各河段的河床累計沖淤過程。 1986—1999年，受龍羊峽水庫建成運用以及降雨等因素的影響，黃河下游枯水歷時增加，河流輸沙動力不足，導致下游基本處于持續淤積的狀態，下游累計淤積量為21 億m3。小浪底水庫蓄水攔沙運用后（2000—2020 年），來沙量減少使得下游轉為劇烈沖刷狀態。 2000—2020 年黃河下游總沖刷量為20 億m3，從沖刷的沿程分布來看，高村以上游蕩段的沖刷量達13.38 億m3，占下游總沖刷量的67%，過渡段和彎曲段的沖刷量相當，分別占17%和16%，表現為上段沖刷幅度大、中段與下段沖刷幅度小的特點［27］。

黃河下游河道的持續沖刷，一方面使沿程各河段床面發生不同程度的粗化，中值粒徑基本在0.05 mm 以上，且粗化程度沿程減弱；另一方面使得黃河下游河床橫斷面形態發生了顯著調整，改變了小浪底水庫運用前黃河下游河槽逐漸萎縮的情況。 小浪底水庫運用后，各河段平灘斷面面積逐年增大且平灘水深持續增加，從而使得河相系數持續減小，其中：游蕩段的減小幅度最大，2020 年汛后河相系數比1999 年減小44%；過渡段和彎曲段的河相系數基本穩定在5.5 m-1／2和4.0 m-1／2。 上述水沙及河床邊界條件的變化，均會引起水流挾沙力的調整。

2.2 河段挾沙力計算結果

2.2.1水力幾何參數與泥沙參數計算結果

1986—2020 年黃河下游游蕩段、過渡段、彎曲段河段平均過水斷面面積年際變幅較大，而平均水深在小浪底水庫運用后顯著增大。 河段平均過水斷面面積在游蕩段、過渡段、彎曲段的取值分別為481 ～2 130 m2、422～2 018 m2、375～1 471 m2；平均水深的變化范圍分別是0.68 ～2.25 m、1.10 ～3.71 m、1.48 ～4.12 m。游蕩段平均流量的變化范圍為375 ～2 505 m3／s，過渡段為289～2 417 m3／s，彎曲段為204～2 396 m3／s；游蕩段平均流速的變化范圍為0.68 ～1.75 m／s，過渡段為0.67～1.99 m／s，彎曲段為0.54～1.97 m／s。

小浪底水庫運用后，黃河下游含沙量較小浪底水庫運用前大幅度減小。 游蕩段各水文斷面平均含沙量由16.98～63.56 kg／m3減小到0.47 ～19.77 kg／m3、過渡段由14.68～46.89 kg／m3減小到0.89～19.72 kg／m3，彎曲段由10.89 ～47.56 kg／m3減小到0.89 ～21.41 kg／m3。1986—2020 年3 個河段的體積比含沙量范圍分別為0.000 2～0.024 0、0.000 3～0.017 7、0.000 3～0.017 9；非均勻懸沙群體沉速范圍分別為0.001 8 ～0.008 2 cm／s、0.001 4～0.005 6 cm／s、0.001 2 ～0.004 5 cm／s；渾水卡門常數的取值在0.31～0.39 之間。

2.2.2挾沙力公式率定結果

1986—2020 年黃河下游游蕩段、過渡段、彎曲段汛期沖淤量分別為-1.44 億～5.59 億m3、-0.42 億～0.55億m3、-0.62 億～0.10 億m3。 取河床總沖淤斷面面積A0為河段汛期沖淤量與河長的比值，時間t為汛期總時長，含沙量S為河段內所有水文斷面含沙量的算術平均值，代入式（7），計算出游蕩段、過渡段、彎曲段的挾沙力分別為0. 24 ～27. 03 kg／m3、0. 57 ～19.38 kg／m3、0.55～19.01 kg／m3。 各河段水沙綜合參數與挾沙力計算值的冪函數關系見圖5。

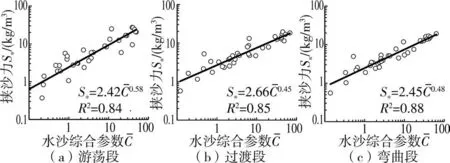
圖5 黃河下游各河段水沙綜合參數與挾沙力計算值的關系

由圖5 可以看出，黃河下游游蕩段、過渡段、彎曲段水沙綜合參數與挾沙力計算值的相關程度總體較高，擬合的冪函數關系決定系數分別為0.84、0.85、0.88。 直線斜率即為挾沙力公式的指數，游蕩段、過渡段、彎曲段指數m分別為0.58、0.45、0.48，進一步得到系數k分別為2.42、2.66、2.45。 結果較為合理，大致接近張紅武公式k＝2.5、m＝0.62 的取值。 采用各河段擬合的冪函數公式可以計算出黃河下游各河段的水流挾沙力。 3 個河段的河段挾沙力取值為0.53 ～23.81 kg／m3、1.02～17.86 kg／m3、0.94 ～18.24 kg／m3，其綜合表示了在河段平均水沙條件下水流挾沙力的大小，采用河段挾沙力計算方法得到的結果在數值上合理。

2.3 河段挾沙力時空變化特點

2.3.1河段挾沙力隨時間變化特點

圖6給出了黃河下游游蕩段、過渡段、彎曲段河段挾沙力逐年變化情況。 1986—1999 年游蕩段河段挾沙力的范圍為8.24～24.00 kg／m3，平均值為16.57 kg／m3；而小浪底水庫運用后，黃河下游游蕩段河段挾沙力大幅度減小，減小至0.52 ～5.57 kg／m3，多年平均值為2.73 kg／m3，較運用前減小了84%。 過渡段河段挾沙力范圍由小浪底水庫運用前的4.54 ～17.74 kg／m3減小至運用后的1.03 ～6.21 kg／m3，多年平均值由12.00 kg／m3減小至3.52 kg／m3，減小了約71%。 彎曲段河段挾沙力由小浪底水庫運用前的3.05～18.34 kg／m3（多年平均值為11.33 kg／m3）減小至0.94～7.46 kg／m3（多年平均值為3.52 kg／m3），減小了69%。 3 個河段的河段挾沙力大致呈現出小浪底水庫運用前逐年波動變化較大，小浪底水庫運用后顯著減小且逐年波動幅度也減小的變化特點。

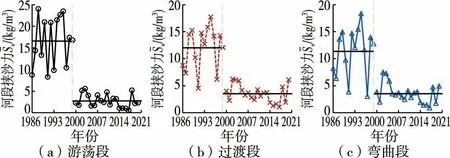
圖6 黃河下游河段挾沙力逐年變化情況

對黃河下游游蕩段、過渡段、彎曲段河段挾沙力的時間變化序列，進行Mann-Kendall 趨勢檢驗和Mann-Kendall 突變檢驗，分析河段挾沙力的變化趨勢及突變態勢。 研究時段內，黃河下游游蕩段、過渡段、彎曲段的β值均小于0，且｜Z｜≥2.58，通過了1%顯著性檢驗，這表明各河段挾沙力在99%的置信區間內呈現顯著性減小趨勢。 經突變檢驗，在置信水平0.01 的基礎上，游蕩段、過渡段、彎曲段河段挾沙力的M-K 統計值由正值轉為負值的年份均發生在1999 年。 這是因為1999 年小浪底水庫運用，水庫的蓄水攔沙作用導致進入黃河下游的水沙條件發生顯著改變，進而導致下游各河段挾沙力轉變為持續減小的狀態。

2.3.2河段挾沙力沿程變化特點

小浪底水庫運用前，河段挾沙力平均值大致呈沿程減小的趨勢，在游蕩段、過渡段、彎曲段分別為16.57、12.00、11.33 kg／m3，沿程減小了32%。 小浪底水庫運用后，河段挾沙力平均值呈沿程增大的變化規律，分別為2.73、3.52、3.52 kg／m3，沿程增大了29%。河段挾沙力明顯地表現出小浪底水庫運用前沿程減小、運用后沿程增大的變化特點（見圖7）。

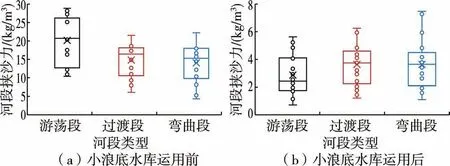
圖7 黃河下游沿程河段挾沙力

小浪底水庫運用前黃河下游床沙中值粒徑沿程變化較小，但河段平均流速沿程先增大后減小，平均水深沿程增大（見圖8），懸沙平均沉速沿程減小了32%，直接導致水沙綜合參數減小了約6%，河段挾沙力沿程減小；此外，含沙量沿程減小使得體積比含沙量沿程減小，使得河段挾沙力從游蕩段到過渡段減小28%，過渡段到彎曲段減小6%。 小浪底水庫運用后，床沙中值粒沿程減小了35%，使得河床的可沖性沿程增大，床沙對水流中粒徑較細的泥沙補給沿程增加，導致河段挾沙力沿程增大；河段平均流速沿程增大了15%，水深沿程增大了63%，懸沙沉速沿程減小幅度增大至45%。 床沙中值粒徑、河段平均流速與懸沙沉速這3個因素的變化共同使得水沙綜合參數增大了69%，導致河段挾沙力沿程增大。

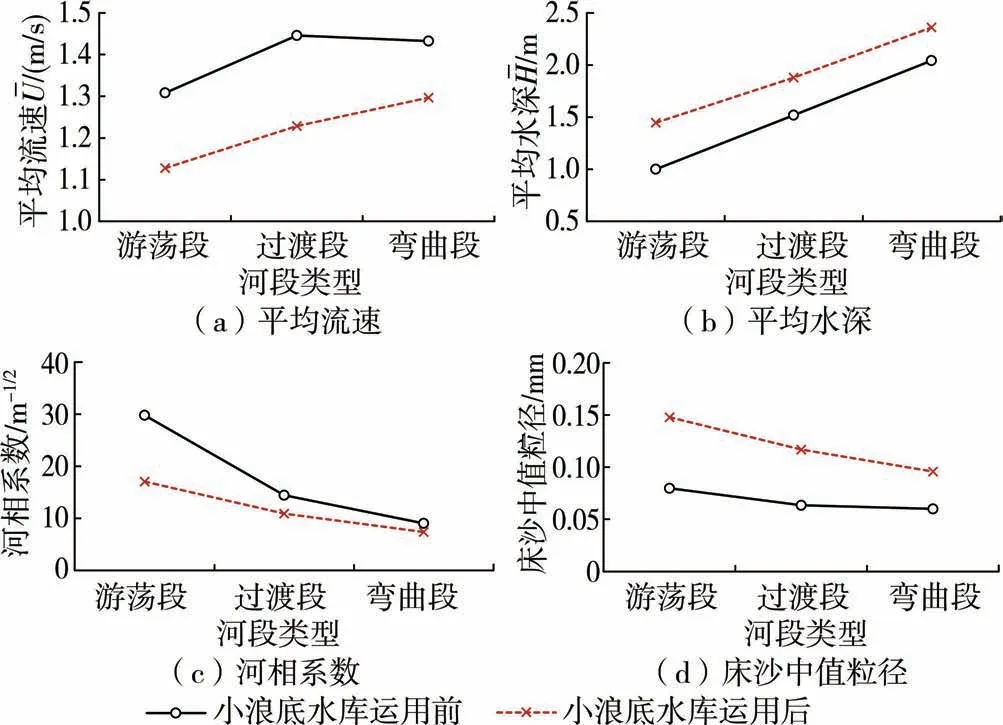
圖8 黃河下游各河段水力要素沿程變化

3 結論

黃河下游河床形態沿程變化很大且實測水文斷面分布不均勻，采用斷面數據計算得到的挾沙力僅能反映特定水文斷面的挾沙能力，因此需要將以往斷面挾沙力的計算方法拓展到河段尺度。 本文的主要結論如下。

1）提出了一種河段水流挾沙力的計算方法。 該方法首先基于1986—2020 年黃河下游7 個水文斷面的汛后地形資料及日均水沙資料，計算河段平均水沙綜合參數。 再根據挾沙力計算值與水沙綜合參數的相關關系，重新率定在河段平均水沙條件下張紅武公式的指數與系數，擬合的相關關系式的決定系數均在0.84以上。 從而得到黃河下游游蕩段、過渡段、彎曲段河段平均條件下挾沙力公式的系數k分別為2.42、2.66、2.45，指數m分別為0.58、0.45、0.48。

2）1986—2020 年游蕩段、過渡段、彎曲段的河段挾沙力范圍分別為0.52～24.00 kg／m3、1.03 ～17.74 kg／m3和0.94 ～18.34 kg／m3。 在時間上，呈現出小浪底水庫運用前年際變化較大，水庫運用后變化顯著減小的特點，河段挾沙力較水庫運用前減小69%以上。 在空間上，小浪底水庫運用前河段挾沙力呈現沿程減小的變化趨勢，總體減小了32%；水庫運用后呈現沿程增大的變化趨勢，增大了約29%。 這是由床沙沿程變細使得床沙對水流中泥沙補給變多以及河槽斷面形態沿程趨于窄深共同導致的。