四元數Lyapunov方程的酉結構解及最佳逼近

黃敬頻,劉廣梅

(廣西民族大學 數學與物理學院, 南寧 530006)

0 引言

Lyapunov矩陣方程AX+XA*=C在系統穩(wěn)定性分析和最優(yōu)控制等領域有十分廣泛的應用,對這類矩陣方程的研究已有較多的成果[1-8],文獻[9]提出了四元數矩陣的Jordan標準形的一種新的算法,文獻[10-11]研究了四元數體上酉矩陣的反問題和四元數矩陣方程的一元矩陣反問題,但關于Lyapunov矩陣方程的酉結構解目前未見相關的研究報道。酉矩陣是一類重要的結構矩陣,它在物理系統進行建模時扮演著重要的角色[12-13]。例如,光學衍射與傳輸過程可以通過酉矩陣進行描述,光量子的糾纏與相互作用也可以通過酉矩陣來刻畫。目的是探討Lyapunov方程的酉結構解及一類最佳逼近問題。

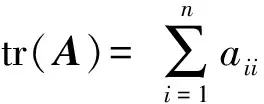
主要討論以下2個問題:

問題1給定2個四元數正規(guī)矩陣A,C∈Qn×n且AC=CA,求四元數酉矩陣X∈Un×n,使得

AX+XA*=C

(1)

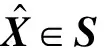
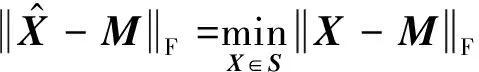
(2)

1 問題1的解

tr(AB)=tr(BA),tr(P-1AP)=tr(A)

一般不再成立,但有以下結果。

引理1[15]設A,B,P∈Qn×n且P可逆,則

(1) Re[tr(AB)]=Re[tr(BA)];

(2) Re[tr(P-1AP)]=Re[tr(A)]。

對于一般的四元數矩陣A∈Qn×n存在上三角Schur分解,而對角線上的元素正是A的右特征值[14]。進一步,當A是正規(guī)矩陣時,總有下面的右特征值分解。

引理2[15](右特征值分解) 設A∈Qn×n是正規(guī)矩陣,rank(A)=r,則存在四元數酉矩陣U∈Un×n使得

A=Udiag(λ1,…,λr,0,…,0)U*

(3)

其中λ1,…,λr∈C是A的非零右特征值且|λ1|≥…≥|λr|>0,i=1,2,…,r。

引理3四元數酉矩陣的右特征值的模總等于1。

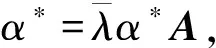
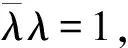
引理4設A,C∈Qn×n為四元數正規(guī)矩陣,則AC=CA成立的充要條件是A,C可同時酉對角化。

證明充分性。設rank(A)=r,若A,C可同時酉對角化,則存在U∈Un×n使得

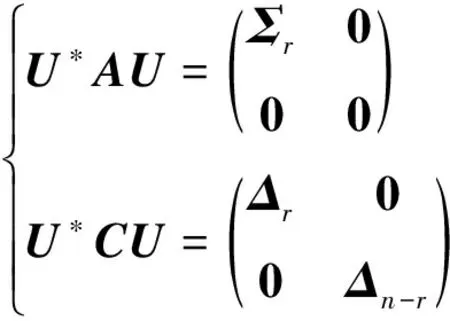
(4)

其中

Σr=diag(λ1,…,λr)∈Cr×r,λi≠0,i=1,…,r

Δr=diag(β1,…,βr)∈Cr×r

Δn-r=diag(βr+1,…,βn)∈C(n-r)×(n-r)

由于兩對角矩陣可交換,從而由式(4)可知AC=CA。

必要性。由于A,C∈Qn×n為四元數正規(guī)矩陣,則存在U∈Un×n使得式(3)成立。設

(5)

其中λ1,λ2,…,λs為互不相同的復數(s≤n)且n1+n2+…+ns=n。由AC=CA知U*AU和U*CU可交換,于是有

U*CU=diag(C1,C2,…,Cs)

(6)

其中Ci(i=1,2,…,s)為正規(guī)矩陣,從而存在四元數酉矩陣V1,V2,…,Vs使得

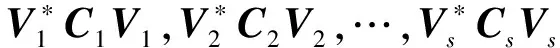
(7)

均為復對角矩陣。因此取

V=diag(V1,V2,…,Vs)U

則V∈Un×n且V*AV和V*CV均為對角矩陣。證畢。

定理1給定A,C∈Qn×n,則問題1存在酉結構解的必要條件是

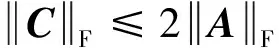
(8)

證明若問題1有解,即存在X∈Un×n使得AX+XA*=C,根據Frobenius范數的三角不等式及酉乘積不變性可得

即不等式(8)成立。證畢。

定理2設X∈Un×n,A∈Qn×n是正規(guī)矩陣,rank(A)=r,A的右特征值分解如式(3),則有

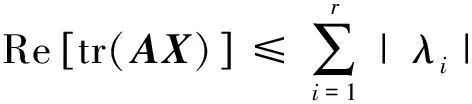
(9)

且等號成立的充分必要條件是

(10)

其中Dr=diag(e-Iθ1, e-Iθ2,…, e-Iθr),θi是λi的輻角主值,G∈U(n-r)×(n-r)是任意的酉矩陣。

證明因為X,U∈Un×n,可知U*XU∈Un×n,設

(11)

其中

X11=(xij)∈Qr×r,X21=(dij)∈Q(n-r)×r

因此有

于是

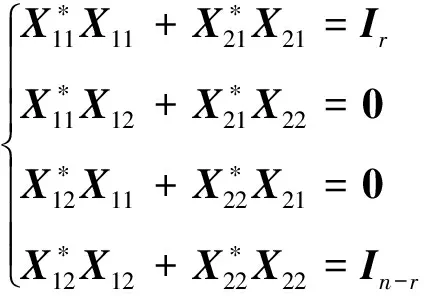
(12)

由此可得

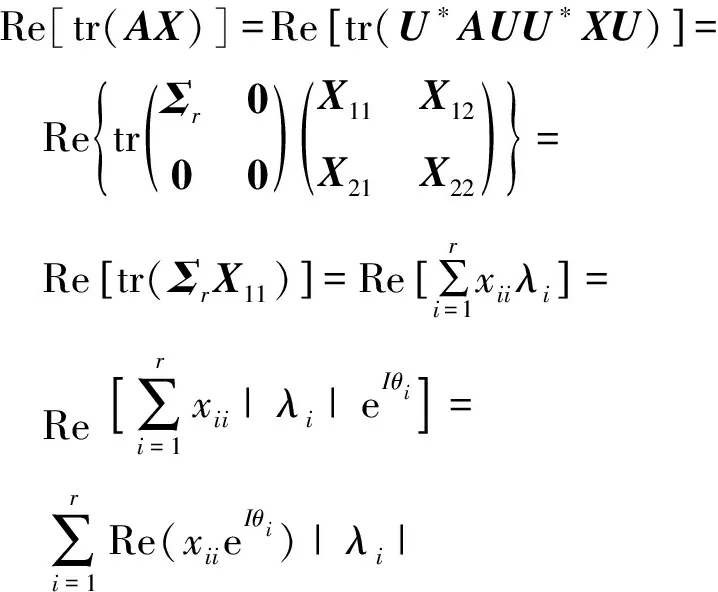
(13)

其中λi=|λi|eIθi=|λi|(cosθi+Isinθi),由式(12)得,對任意的1≤i≤r有

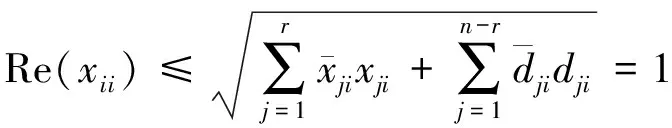
(14)

因此有Re(xiieIθi)≤1,從而由式(13)和(14)可得

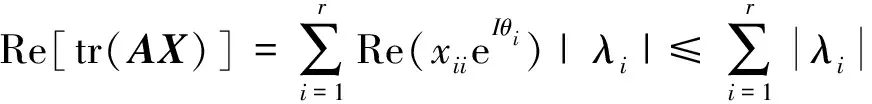
(15)

當Re(xiieIθi)=1時,式(15)等號成立,且有xii=e-Iθi(i=1,2,…,r),這時結合式(12)知

X11=diag(e-Iθ1, e-Iθ2,…, e-Iθr)

X21=0,X12=0,X22=G∈U(n-r)×(n-r)

再由式(11)可知X可表示為式(10)。于是式(9)等號成立的充分必要條件是式(10)成立。證畢。

根據定理2,可以推導出方程(1)存在酉結構解的另一個必要條件:

推論1給定A,C∈Qn×n,A是正規(guī)矩陣,rank(A)=r,A的右特征值分解如式(3),則問題1存在酉結構解的必要條件是

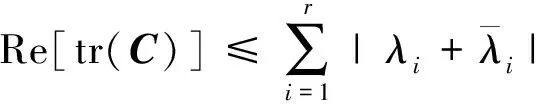
(16)

證明若問題1有解,即存在X∈Un×n使得AX+XA*=C,根據引理1可得

Re[tr(C)]=Re[tr(AX+XA*)]=

Re[tr(AX)]+Re[tr(XA*)]=

Re[tr(AX)]+Re[tr(A*X)]=

Re[tr(A+A*)X]

(17)

由于

因此根據定理2 中不等式(9)和式(17)可得

即不等式(16)成立。證畢。

為給出方程(1)存在酉結構解的充要條件,對于分解式(4)中的U∈Un×n,記

(18)

于是有下列結果。

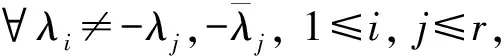
(19)

有解時,其通解表達式為

(20)

其中

G∈U(n-r)×(n-r)是任意的四元數酉矩陣。

證明根據引理4知,存在U∈Un×n使得式(4)成立。因此方程(1)等價于

U*AUU*XU+U*XU(U*AU)*=U*CU

(21)

把式(4)和式(18)代入式(21)得

(22)

由式(22)可得

X12=0,X21=0,Δn-r=0

(23)

且

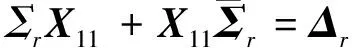
(24)

下面求解方程(24)。方程(24)等價于

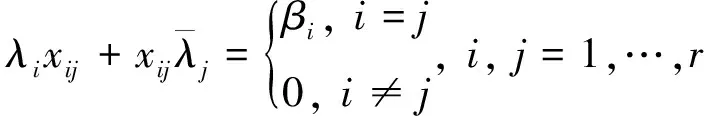
(25)

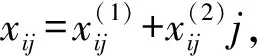
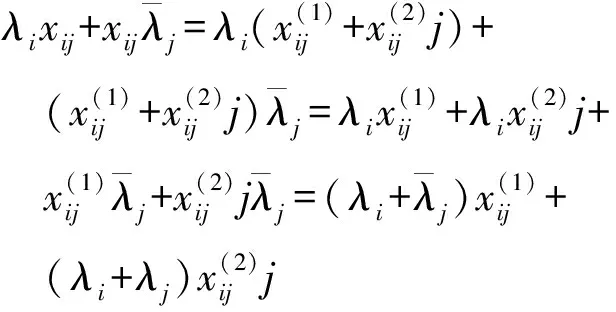
(26)

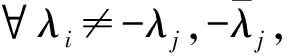
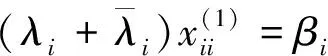
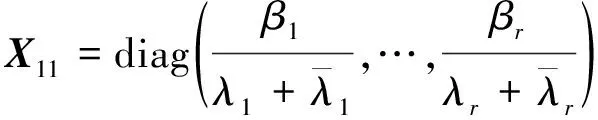
(27)

根據式(23)知X12=0,X21=0,因此由式(18)可得

U*XU∈Un×n?X11∈Ur×r,X22∈U(n-r)×(n-r)

再由式(27)得

于是問題1有解的充要條件是式(19)成立。有解時,其通解表達式為式(20)。證畢。

2 問題2的解

由問題1的求解過程可知,在定理3的條件下,問題1的解集S≠?。當M∈Un×n是已知酉矩陣時,對矩陣U*MU作如下分塊:

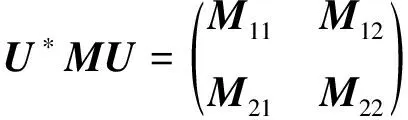
(28)

其中U由分解式(4)給出,且

M11∈Qr×r,M12∈Qr×(n-r)

M21∈Q(n-r)×r,M22∈Q(n-r)×(n-r)

設rank(M22)=k(0≤k≤n-r),并對M22作奇異值分解如下:

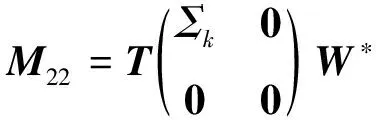
(29)

其中

T,W∈U(n-r)×(n-r)

Σk=diag(η1,η2,…,ηk)>0

下面給出問題2的最佳逼近解。

定理4在定理3的條件下,設問題1的解集為S,M∈Un×n是已知酉矩陣,對矩陣U*MU作分塊式(28),并對M22作奇異值分解(29),則問題2的最佳逼近解存在,且有如下表達式:

(30)

其中U,Dr由式(20)給出,T,W∈U(n-r)×(n-r)由式(29)給出,Z∈U(n-r-k)×(n-r-k)是任意的。

證明當X∈S時,由通解表達式(20)和式(28),以及Frobenius范數酉乘積不變性得

(31)

其中G∈U(n-r)×(n-r)。因此由式(31)可知

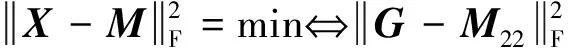
(32)

又因為

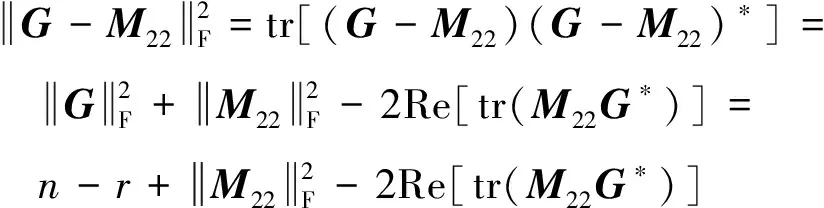
(33)

所以由式(33)得

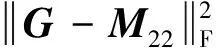
類似于定理2的證明可得

Re[tr(M22G*)]=max

當且僅當

也就是

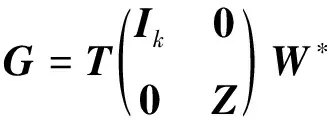
(34)

其中Ik是k階單位矩陣,Z∈U(n-r-k)×(n-r-k)。把式(34)代入式(20)即得問題2的最佳逼近解為式(30)。證畢。

3 求解步驟

根據定理3和定理4的結果,給出問題1和問題2的求解步驟如下:

步驟1對給定的四元數正規(guī)矩陣A,C∈Qn×n,寫出A,C的復分解,即

A=A1+A2j,C=C1+C2j,

A,A2,C1,C2∈Cn×n

步驟2檢驗條件AC=CA是否成立。若成立,則進行下一步。

步驟3對A,C進行右特征值分解,從而得出分解式(4)。

步驟4檢驗條件(19)是否成立。若成立,則進行下一步。

步驟5按定理3的結果寫出酉結構矩陣(20),即得問題1的一般酉結構解X。

步驟6對矩陣U*MU作四分塊(28),并對M22作奇異值分解(29)。

最后進行誤差檢驗。定義問題1的誤差值和問題2的最佳逼近值如下:

當Er(X)是一個充分小的數值時,認為所得的酉結構解X是接近真值的。

4 數值例子

給定下列2個四元數矩A,C∈Q4×4:

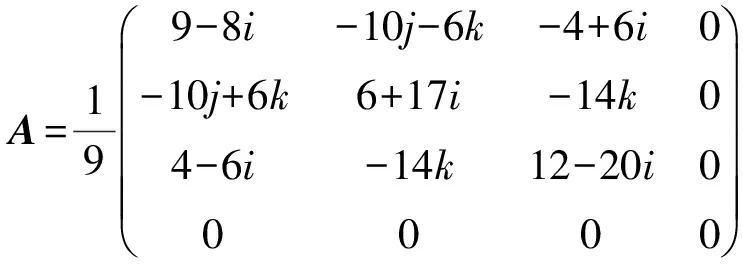
1) 討論Lyapunov方程AX+XA*=C的酉結構解是否存在。若存在,求其酉結構解集S。

解1) 先寫出A,C的復分解:

直接計算可知A,C是正規(guī)矩陣且滿足交換AC=CA。下面對四元數矩陣A,C同時作右特征值分解可得

其中

λ1=1+4i,λ2=2+i,λ3=0,λ4=0

β1=2i,β2=2.4+3.2i,β3=0,β4=0

且

根據A,C的右特征值分解式可知rank(A)= rank(C)=2并且

根據定理3可知,所給方程AX+XA*=C的酉結構解存在,且其酉結構解表達式為:

其中

diag(i,0.6+0.8i)∈U2×2

G∈U2×2是任意的四元數酉矩陣。經計算得誤差值為:

2) 當M=diag(1,i,j,k)∈U4×4時,得

其中

根據定理4可得

于是由式(30)可知問題2的最佳逼近解為:

經計算可知最佳逼近值為:

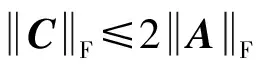
5 結論

Lyapunov方程AX+XA*=C是一類應用廣泛的矩陣方程,在四元數體上討論它的酉結構解及最佳逼近問題。針對問題1,分析了與A可交換的矩陣的特征結構并利用四元數矩陣的右特征值分解,以及四元數矩陣Frobenius范數酉乘積不變性,得到了四元數Lyapunov方程存在酉結構解的充要條件并給出一般解的表達式。針對問題2,利用酉矩陣的性質和矩陣的分塊方法,在問題1酉結構解集S≠?的前提下,獲得S與預先給定的四元數酉矩陣M有極小Frobenius范數的最佳逼近解。所得結果拓廣了Lyapunov方程在四元數體中的新類型結構解。