基于超聲波測試的片巖單軸抗壓強度預測模型

管華棟，潘 熙，黃雅蘭

(1.江西理工大學土木與測繪工程學院，江西贛州 341000；2.江西理工大學材料冶金化學學部，江西贛州 341000)

0 引 言

材料的單軸抗壓強度是指在單一軸向荷載條件下，材料破壞時的極限壓應力。在巖土工程中，單軸抗壓強度是巖石最基本也是重要的力學參數之一，被廣泛用于支護設計、巖體質量分級、圍巖穩定性分析等方面[1]。巖石單軸抗壓強度主要是通過室內單軸抗壓試驗直接獲取，但試驗操作耗時，成本高昂，而且對巖石試件的完整性要求較高，許多學者開展了巖石單軸抗壓強度的預測研究，以期建立快速、方便、經濟的間接預測法。

目前，國內外學者針對巖石單軸抗壓強度預測開展過大量研究：有學者基于點載荷試驗、施密特錘試驗和塊體沖擊指數試驗等進行單軸抗壓強度的估算[2-3]，也有學者[4-10]基于縱波波速建立了巖石單軸抗壓強度的回歸預測模型；還有部分學者[11-12]基于靜彈性模量建立了泥巖和砂巖等的單軸抗壓強度非線性預測模型；而李文等[13]則從量綱平衡的角度，基于縱波模量建立了安英斑巖和頁巖的單軸抗壓強度線性回歸預測模型。此外，還有學者通過神經網絡算法[14-15]、數字鉆探技術[16-17]和X射線CT掃描試驗[18]等新方法來預測單軸抗壓強度。縱觀這些預測方法和手段，作者認為操作最快捷、簡單、經濟的應該是基于巖石聲學參數與力學參數之間的相互聯系所建立的巖石單軸抗壓強度預測模型。當前的研究對象中，幾乎沒有涉及到片巖，因此，本文基于福建某礦山鉆取的巖樣，開展巖石超聲波試驗，進行巖石單軸抗壓強度與各聲學參量的回歸分析，并最終建立基于動彈性模量的片巖單軸抗壓強度預測模型，進而為發展超聲波測試技術的相關理論研究和工程應用提供幫助和參考。

1 巖石超聲波試驗和單軸壓縮試驗

試驗所用片巖巖樣來自福建某礦山。該礦區巖體呈塊狀結構，由云母斜長變粒巖、斜長云母石英片巖、構造角礫巖組成，屬于堅硬類型，完整性中等，弱風化，裂隙不發育。在井下標高為575 m的采空區，設置兩個鉆孔，鉆孔間相距10 m，每個鉆孔各取8個巖樣，其物理參數統計如表1所示[19-20]。

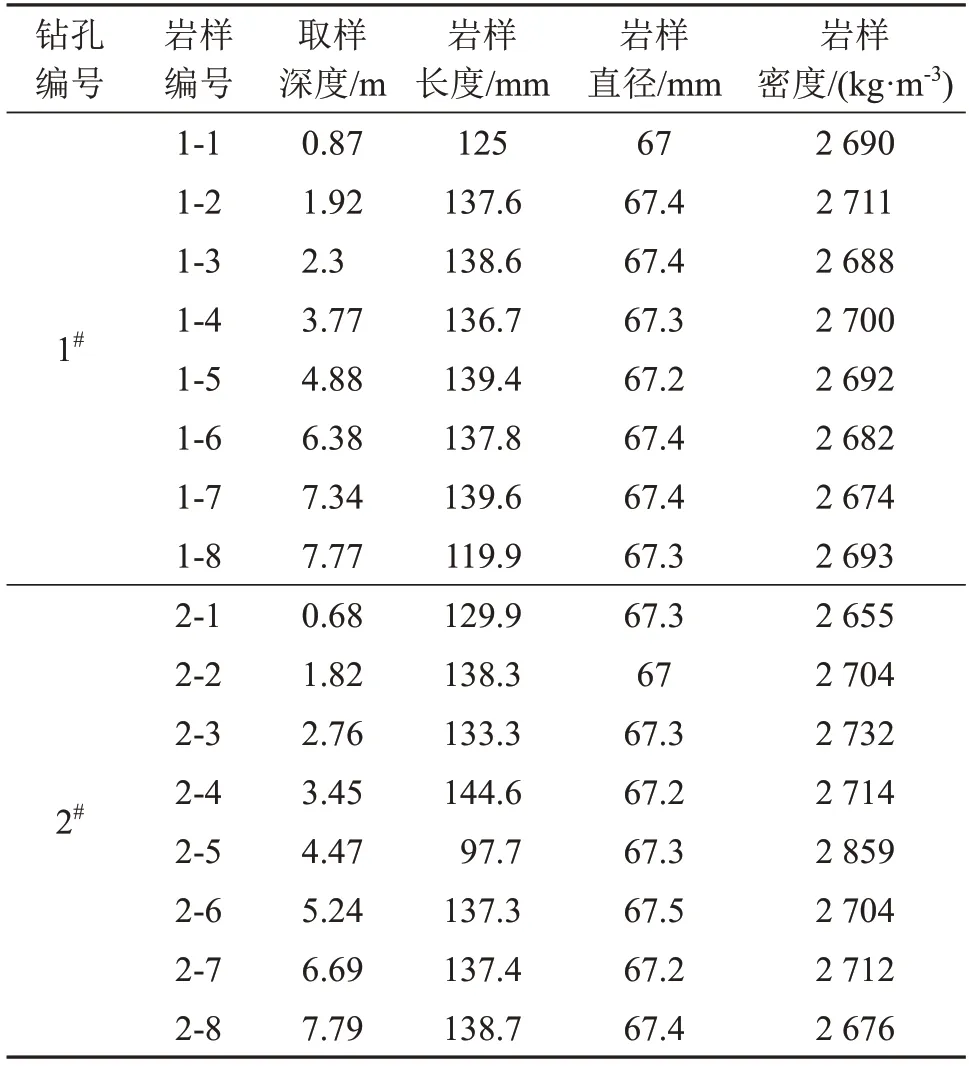
表1 巖樣物理參數統計Table 1 The physical parameters of rock specimens

為了進行片巖的單軸抗壓強度回歸分析，首先進行巖石超聲波試驗，獲取巖石超聲波縱、橫波波速等相關參數，再進行巖石單軸壓縮試驗，獲取巖石彈性模量和單軸抗壓強度參數。

1.1 巖石超聲波試驗

巖石超聲波波速測試采用的是RSM-SY5 型數字式超聲波儀(產自武漢中科智創)，用縱波換能器測試巖樣的縱波波速，用橫波換能器測試巖樣的橫波波速測得波速后依據式(1)可計算動彈性模量，依據式(2)[13]可計算縱波模量和橫波模量。

式中：Ed為動彈性模量，單位為GPa；ρ為密度，單位為kg·m-3；vp為縱波波速，單位為m·s-1；vs為橫波波速，單位為m·s-1。

式中：Pp為縱波模量，單位為GPa；Ps為橫波模量，單位為GPa。

1.2 巖石單軸壓縮試驗

巖石單軸壓縮試驗采用的是RMT-150C巖石力學試驗系統，加載方式為位移控制模式。由于選用的部分巖樣長徑比不符合標準，因此需要對巖樣抗壓強度和靜彈性模量的試驗值進行尺寸效應修正，得到標準試樣下的抗壓強度和靜彈性模量，結果如表2所示[19-20]。表2中Es為靜彈性模量，σc為單軸抗壓強度。

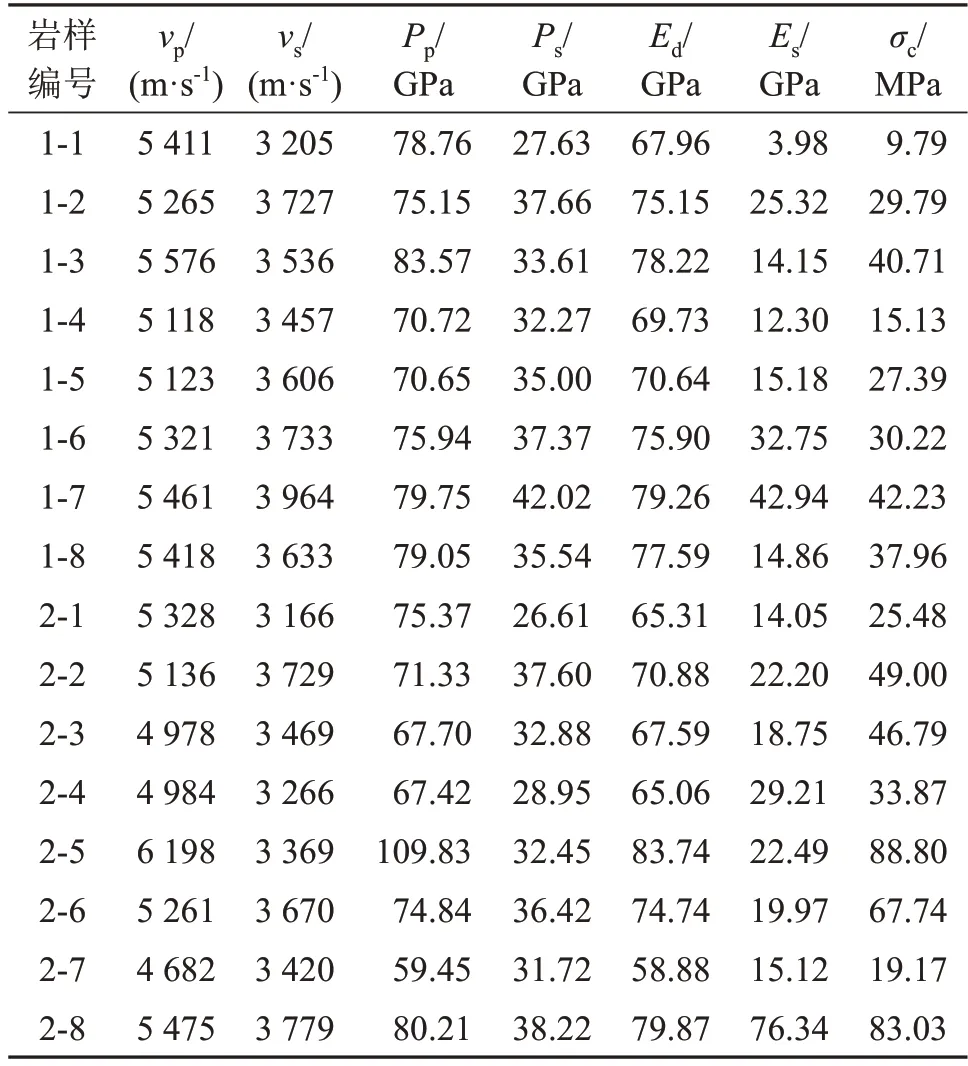
表2 巖樣試驗結果統計Table 2 Statistics of test results of rock specimens

2 試驗結果分析

基于試驗統計數據，分別進行兩個鉆孔的片巖單軸抗壓強度σc與縱波波速vp、橫波波速vs、縱波模量Pp、橫波模量Ps、動彈性模量Ed以及靜彈性模量Es的回歸分析。

2.1 巖石單軸抗壓強度的敏感度分析

本文采用非參數統計方法對巖石單軸抗壓強度進行敏感性分析，引入敏感性系數。敏感性系數越大，表明參數xi對研究對象y的變化越敏感。敏感系數S的計算公式為

式中：xi為巖樣某一參數取值大小，無量綱；y為巖樣的單軸抗壓強度取值大小，無量綱；Cov(·)表示求協方差；σxi、σy分別為xi和y的標準方差，無量綱。

利用式(3)分別計算巖樣的密度、縱橫波速、縱橫波模量、動靜彈性模量對單軸抗壓強度變化的敏感性系數。巖樣單軸抗壓強度的敏感性分析結果如圖1所示。

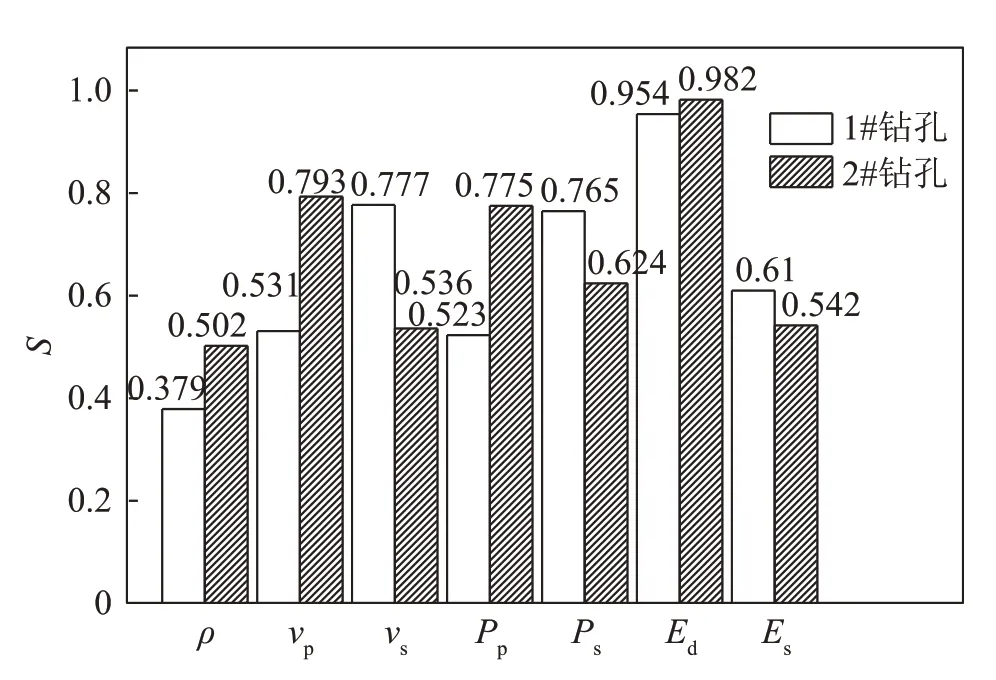
圖1 巖樣單軸抗壓強度的敏感性分析結果Fig.1 Sensitivity analysis results of uniaxial compressive strength for rock specimens

從圖1中可以看出，1#鉆孔中各參量對單軸抗壓強度變化的敏感度排序從小到大依次為：密度、縱波模量、縱波波速、靜彈性模量、橫波模量、橫波波速、動彈性模量。2#鉆孔中各參量對單軸抗壓強度變化的敏感度排序從小到大依次為：密度、靜彈性模量、橫波波速、橫波模量、縱波模量、縱波波速、動彈性模量。從敏感度排序可以看出，1#鉆孔和2#鉆孔中對單軸抗壓強度變化最不敏感的參量是密度，對應的敏感性系數分別為0.379 和0.502；1#鉆孔和2#鉆孔中對單軸抗壓強度變化最敏感的參量都是動彈性模量，對應的敏感系數分別為0.954和0.982。

2.2 巖石單軸抗壓強度的回歸分析

基于巖樣單軸抗壓強度的敏感性分析，選擇最敏感參量——動彈性模量Ed建立單軸抗壓強度σc的回歸模型。首先，繪制片巖動彈性模量Ed與單軸抗壓強度σc的散點圖，如圖2所示。兩個鉆孔的片巖單軸抗壓強度與動彈性模量都呈遞增關系，且相關性較強。除了個別巖樣，兩個鉆孔的片巖單軸抗壓強度基本都隨著動彈性模量的增大而增大，即呈正相關關系。

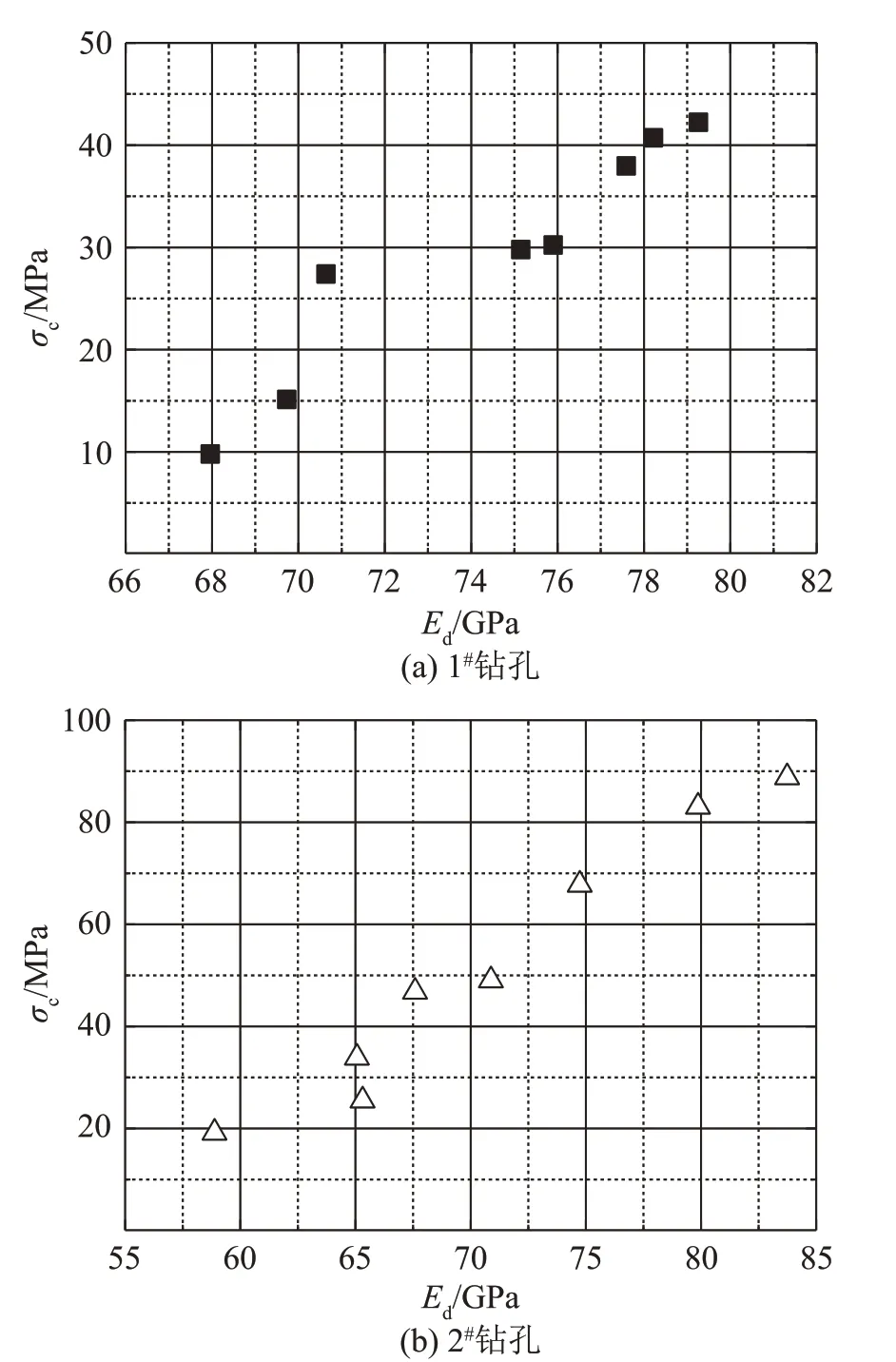
圖2 兩個鉆孔巖樣的Ed-σc關系Fig.2 Relationship between Ed and σc for the specimens from two different boreholes

利用多種函數進行回歸擬合分析，得到兩個鉆孔的片巖單軸抗壓強度與動彈性模量的回歸方程結果如表3所示。按照擬合度R2排序，針對本文中兩個鉆孔的片巖巖樣，單軸抗壓強度與動彈性模量最佳回歸關系應該用多項式模型來描述。

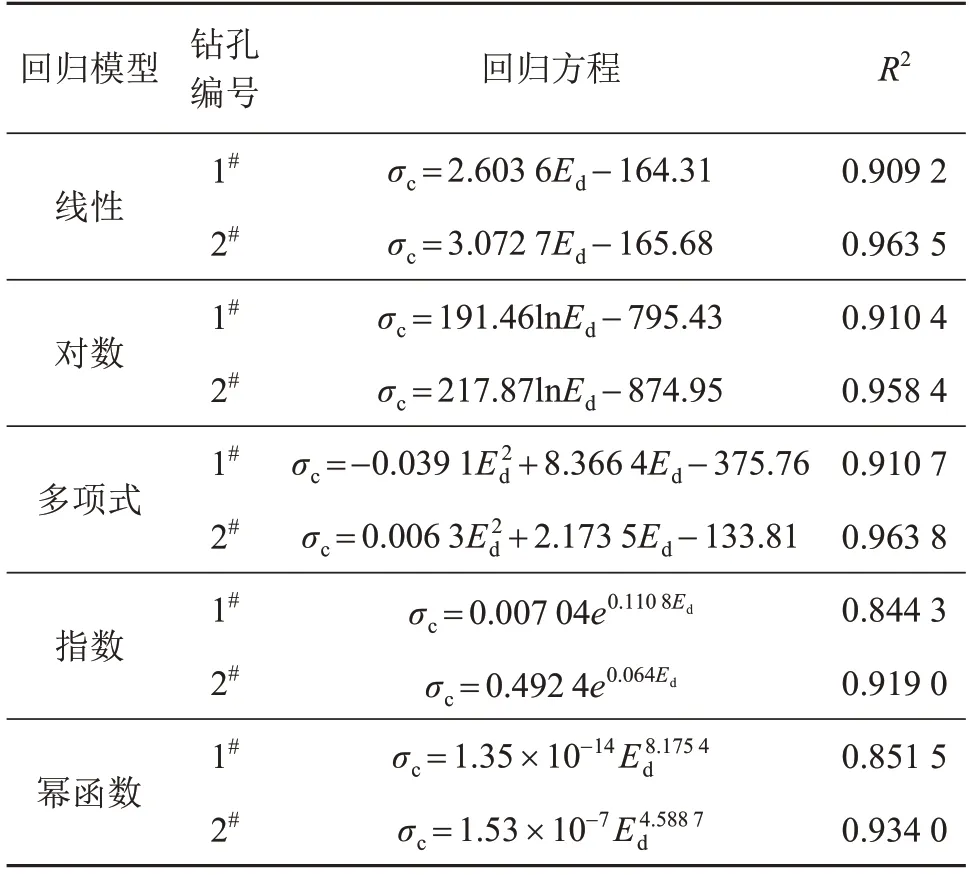
表3 Ed-σc的回歸關系擬合結果Table 3 Regression fitting results of Ed-σc relationship

此外，兩個鉆孔之間，各種回歸模型的擬合度相差不大，即片巖巖樣的空間變異性影響在單軸抗壓強度與動彈性模量的回歸關系中表現得并不明顯。1#、2#鉆孔中各參量巖樣試驗統計結果分別如表4、5 所示。兩個鉆孔中其他參數建立的單軸抗壓強度回歸模型的擬合度相差都較大，也再次說明動彈性模量比這些參量更適合建立單軸抗壓強度的預測模型。

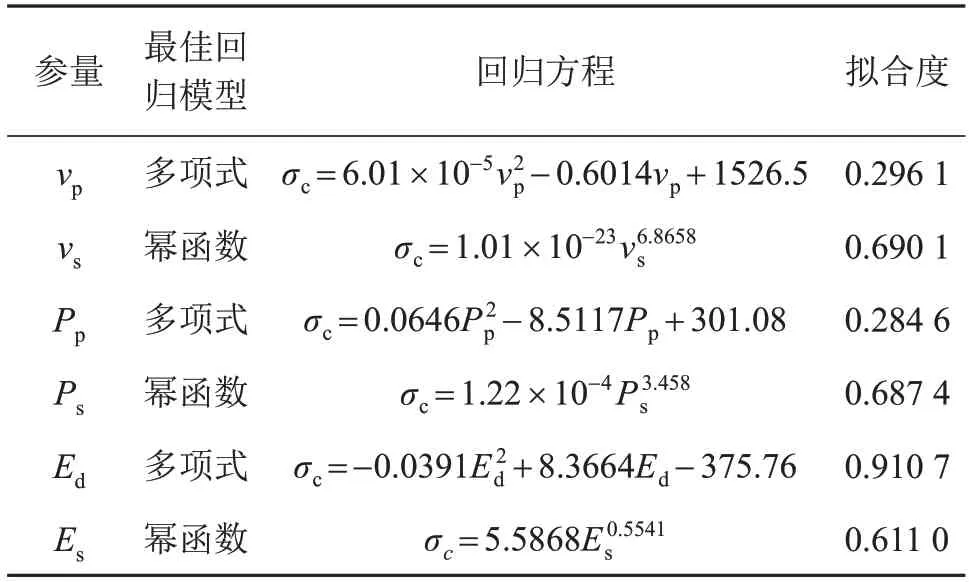
表4 1#鉆孔中各參量巖樣試驗結果統計Table 4 Test result statistics of various parameters of the rock specimen in 1# borehole

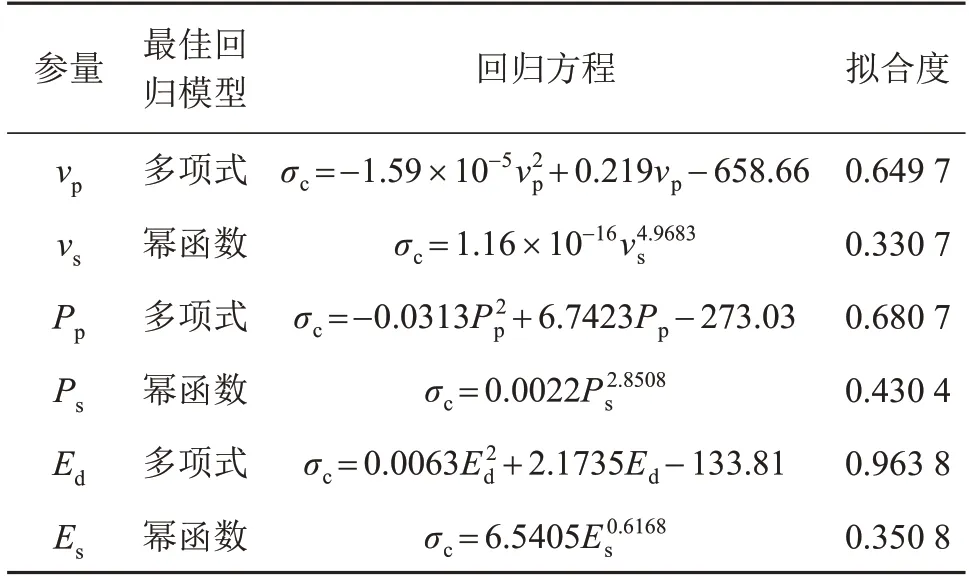
表5 2#鉆孔中各參量巖樣試驗結果統計Table 5 Test result statistics of various parameters of the rock specimen in 2# borehole

基于上述分析，對比表4、5，單軸抗壓強度與動彈性模量的擬合度大于其他參量，且兩個鉆孔的片巖巖樣都滿足這一規律。由式(1)可知，動彈性模量的計算公式中包含了密度、縱波波速和橫波波速，因此動彈性模量比縱波波速或縱波模量更能綜合體現巖石特性。從量綱平衡的角度分析，靜彈性模量和縱波模量都與抗壓強度的量綱一致，單位為ML-1T-2，因此文獻[11-12]和文獻[13]分別基于靜彈性模量和縱波模量成功建立了巖石單軸抗壓強度的預測模型。而動彈性模量的單位也是ML-1T-2，因此基于動彈性模量建立巖石單軸抗壓強度預測模型也是可靠的。此外，基于超聲波測試獲取巖石動彈性模量要比基于單軸壓縮試驗獲取巖石靜彈性模量更簡單、經濟。因此，針對本文的片巖巖樣，采用動彈性模量建立巖石單軸抗壓強度預測模型更加合理、可靠。

3 片巖單軸抗壓強度預測模型

在表3中，僅從擬合度R2來看，單軸抗壓強度與動彈性模量的最佳回歸模型是多項式模型。但線性模型、對數模型與多項式模型的擬合度實際都相差不大，1#鉆孔相差0.001 5，2#鉆孔相差0.005 4。因此，需要進一步對三種模型開展以下檢驗和分析，從而確定基于動彈性模量的片巖單軸抗壓強度最佳預測模型。

3.1 巖石單軸抗壓強度的回歸分析

本文參照文獻[12-13]，采用F檢驗法對三種回歸模型進行回歸方程的檢驗。統計結果如表6 所示。由表6可知，三種回歸模型的F值均大于顯著水平為0.05的F檢驗臨界值。因此三種模型對應的回歸方程都是顯著的。

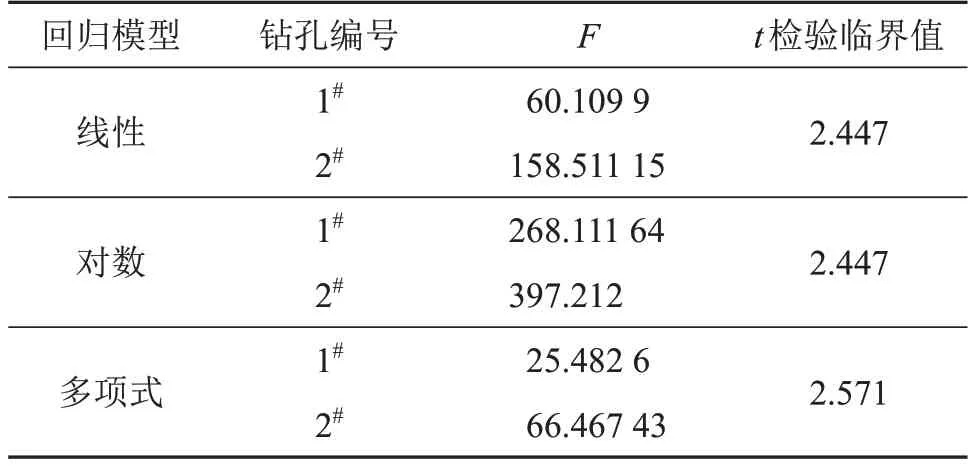
表6 三種模型的回歸方程F值統計Table 6 Statistics of F value of regression equation for three models

3.2 巖石單軸抗壓強度的回歸分析統計結果

分析三種模型的回歸系數，結果如表7所示，線性模型和對數模型的回歸系數t的絕對值均大于顯著水平為0.05的t檢驗臨界值，而多項式模型的回歸系數的t絕對值均小于顯著水平為0.05的t檢驗臨界值。因此，多項式模型的回歸系數未通過回歸系數顯著性檢驗。

表7 三種模型的回歸系數t的值統計結果Table 7 Statistics of t value of regression coefficients for three models

依據表3，兩個鉆孔片巖單軸抗壓強度的線性模型的擬合度平均為0.936 4，對數模型的擬合度平均為0.934 4。因此，從平均擬合度來看，線性模型優于對數模型；此外，線性模型也比對數模型更簡單，更便于使用。綜上，本文建議采用簡單的線性模型來建立基于動彈性模量的片巖單軸抗壓強度預測模型，預測公式為

σc=AEd+B(4)

式中：A為回歸系數；B為修正值，單位為MPa。

4 結 論

本文基于片巖的超聲波試驗和單軸抗壓試驗，開展了片巖單軸抗壓強度與各參量的回歸性分析，得到了以下結論：

(1) 分別得到了片巖單軸抗壓強度與縱波波速、橫波波速、縱波模量、橫波模量、動彈性模量以及靜彈性模量的最佳回歸模型及回歸方程；

(2) 由于受到片巖巖樣的空間變異性和各向異性影響，不同鉆孔中的片巖無法統一采用縱、橫波波速或者縱、橫波模量來建立巖石單軸抗壓強度的最佳回歸模型；

(3) 在片巖所有參量中，動彈性模量受巖樣的空間變異性和各向異性的影響最小，可以在不同鉆孔中建立統一的最佳回歸模型，而且擬合度最高；

(4) 結合擬合度、包含參量、量綱平衡、測試方法以及顯著性分析，基于動彈性模量建立了片巖單軸抗壓強度的最佳預測模型——線性模型，并闡述了其合理性、可靠性和便捷性。