基于聲學黑洞的復合隔聲結構聲學特性研究及試驗

余勇花，吳天歌，楊淇，葉錦嘯，夏兆旺,2

(1.江蘇科技大學能源與動力學院，江蘇鎮江 212003；2.江蘇海事職業技術學院船舶與海洋工程學院，江蘇南京 211170)

0 引 言

隨著社會的發展，噪聲污染越來越受到人們的重視[1-3]。復合隔聲結構一般由平板、阻尼層、穿孔板及多孔吸聲材料等組成。相較于傳統單板結構，在面密度相近時，復合隔聲結構具有更好的隔聲性能[4]。夏兆旺等[5]研究了嵌入式質量塊對隔聲門低頻段隔聲性能的影響，通過有限元法建立兩個相鄰混響室計算隔聲門的隔聲量(Sound Transmis‐sion Loss,STL)。Liu[6]研究了板、空氣、多孔材料間的耦合關系，分析總結了結構組合類型對復合板隔聲性能的影響。

聲學黑洞的引入為復合隔聲結構的發展增添了新的活力[7]。聲學黑洞的結構厚度滿足冪指數函數形式。在理想情況下彎曲波速可以減小到0，可實現彎曲波的零反射[8]。1989 年，Krylov[9]研究了楔形的一維梁結構操縱彎曲波的傳播。王博涵等[10]研究了內嵌聲學黑洞薄板振動數值模擬方法，結果表明合理調節聲學黑洞區域的厚度梯度變化尺度以及冪律會改變局部模態參數。劉波濤等[11]研究了聲學黑洞輕質超結構的低頻帶寬高效隔聲機理，設計了一種針對低頻的新型聲學黑洞超結構。王小東等[12]針對直升機駕駛艙的噪聲問題，提出了基于聲學黑洞的兩種減振降噪方案，在結構總質量不增加的情況下，室內平均噪聲水平在1/3倍頻程內降低了3～10 dB。

本文將聲學黑洞引入復合隔聲結構的設計中，推導了包含多孔材料與穿孔板等參數的復合隔聲結構傳遞矩陣，進而得到復合隔聲結構隔聲量，通過有限元法建立的聲學黑洞復合隔聲結構仿真模型，分析了聲學黑洞的數量、黏彈性阻尼層、半徑等參數對結構隔聲量的影響規律。本文的研究結果為高隔聲量、低面密度的復合隔聲板結構設計提供了新思路。

1 聲學黑洞復合隔聲結構理論基礎

1.1 聲學黑洞結構振動波傳遞特性

嵌入二維聲學黑洞的圓板如圖1所示。原板厚度和半徑之間的關系式為

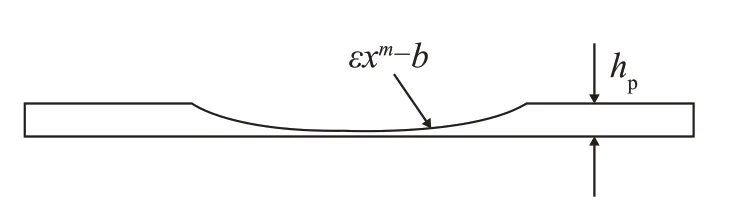
圖1 嵌入二維聲學黑洞的薄板Fig.1 Plate embedded with a two-dimensional ABH

式中：h為黑洞板的厚度；r為黑洞的半徑；ε為常數；m為正有理數，被稱為黑洞效應指數因子；b為黑洞中心到坐標原點的距離；hp為均勻板區域的厚度。彎曲波在各向同性薄板中的傳播速度為，

式中：B為彎曲剛度，B=Eh3(x) [12(1-v2)]；E為楊氏模量，v是泊松比；ω是角頻率；M是板的面密度。

1.2 復合隔聲結構隔聲特性

對復合隔聲結構進行簡化處理：將復合隔聲結構看作n層不同材質的組合結構，每層結構為獨立的聲學單元，聲波從一側入射后，從另一側輻射，則通過復合隔聲結構兩側的聲壓與速度可建立四端參數模型，模型示意圖如圖2所示。

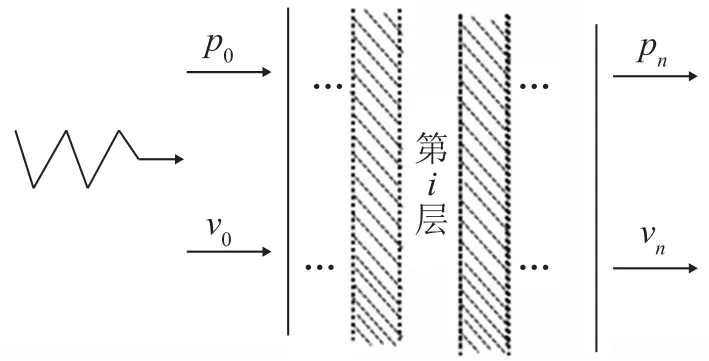
圖2 復合隔聲結構四端參數模型示意圖Fig.2 The four-pole parameter model of multilayer sound insulation structure

以第i層為對象，其前后表面的聲壓和速度可通過二階傳遞矩陣表示：

式中：li為材料層厚度，ci為材料層的速度，ki為材料層的波數，ω為角頻率，ρi為第i層介質密度，Ki為第i層介質的體積彈性模量。

第i層前后表面的聲壓和速度可通過二階傳遞矩陣表示：

式中：pi與vi分別為入射聲壓與速度；pi+1與vi+1分別為輻射聲壓與速度。

第i層介質的聲壓pi與速度vi間的關系用其阻抗表示：

由式(5)可得到：

由式(3)和式(4)可得到第i層聲壓傳遞關系：

式中：k0為空氣的波數，ρ0為空氣的密度。

則復合隔聲結構聲壓總的傳遞關系為

進而得到復合隔聲結構的隔聲量為

2 復合隔聲結構的聲學仿真模型

2.1 隔聲仿真聲腔建模

在隔聲結構隔聲性能的仿真分析中，需要構建模擬試驗測試的雙混響空間。設計一個滿足均勻聲場的混響空間，混響空間的長寬高比例為Lx∶Ly∶Lz=0.9∶1.2∶1.4。在混響室內壁設置不同半徑的半球形突起以實現混響空間內的每個頻段都具有很好的擴散效果[13]。在商業軟件COMSOL 中建立兩個混響室，其中聲源室尺寸為1 m×1.34 m×1.56 m，受聲室的尺寸為1.5 m×2 m×2.3 m。在混響室按照ISO 10140—2[14]的附錄D建立點聲源和測點，聲源為無指向性聲源。模型整體采用六面體網格，且滿足每個波長內至少包含6個單元。隔聲分析仿真聲腔模型如圖3所示。

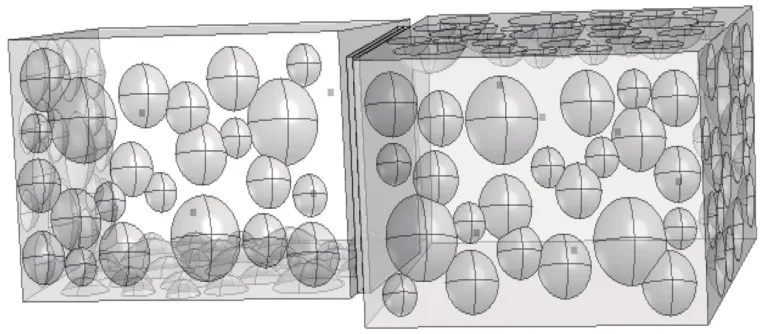
圖3 隔聲分析的聲腔模型Fig.3 Acoustic cavity model for sound insulation analysis

2.2 復合隔聲結構仿真模型驗證

隔聲試驗采用混響室-混響室隔聲試驗方法，測試所用的混響室尺寸為：聲源室5.9 m×5.6 m×4.9 m，接收室5.9 m×3.7 m×4.1 m，依據ISO 10140—2[14]中的測試標準，參照ISO 717—1[15]中的評價標準進行單值評價。

隔聲量的計算公式為

式中：ζ表示聲源位于位置1或位置2；Lζ1、Lζ2分別為經背景噪聲修正后的聲源室和接收室能量平均聲壓級；S為試件安裝測試洞口面積；D=0.16V/TR為接收室吸聲量，V為接收室容積，TR為接收室混響時間。復合隔聲結構的試驗平均隔聲量為

實驗構件安裝在聲源室與受聲室間的窗口。試驗布設照片如圖4所示。

復合隔聲結構模型由隔聲板、阻尼層、多孔材料層、中間薄板以及穿孔板組成。復合隔聲結構如圖5所示。

圖5 復合隔聲結構示意圖Fig.5 Schematic diagram of the composite sound insulation structure

復合隔聲結構的平面尺寸為1 m×1 m，多孔材料為玻璃棉，外平板與中間薄板為鋼板，穿孔板為鋁板，阻尼材料為黏彈性阻尼膠，各層材料參數如表1和表2所示。

表1 復合隔聲結構的材料參數Table 1 Material parameters of composite sound insulation structure

表2 多孔材料參數Table 2 Porous material parameters

整個復合隔聲結構安裝于雙混響室之間，穿孔板側位于聲源室，隔聲板側位于接收室，隔聲板四周采用固定約束。其中外平板厚度為1.5 mm，多孔材料均為25 mm，中間薄板0.1 mm，阻尼層厚度為2 mm，穿孔板厚度為1 mm(穿孔率為10%，孔徑為4 mm)，試驗與仿真隔聲量對比如圖6所示。

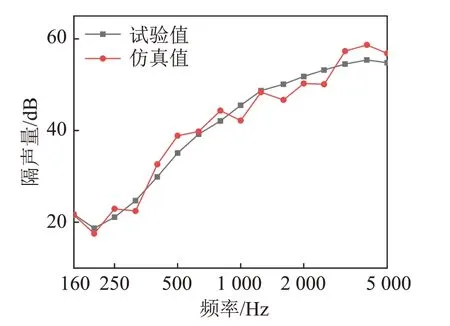
圖6 隔聲量的測試與仿真結果對比Fig.6 Comparison of simulated and tested results of STL

由圖6可知：在160～5 000 Hz頻段范圍內，復合結構隔聲量的仿真值為36.6 dB，實驗單值為36.1 dB。復合結構隔聲量的試驗值與仿真值誤差為0.5 dB。試驗與仿真對比結果表明：復合隔聲結構隔聲量仿真與試驗結果具有較好的一致性，因此采用的仿真分析方法是可行的。

圖7 為1.5 mm 鋼板與1.5 mm ABH 板的隔聲量對比圖。由圖7可知：在160～1 000 Hz頻率范圍內，1.5 mm鋼板的仿真結果與試驗結果具有很好的一致性，采用的仿真方法是可行的。在整個頻段內，相較于1.5 mm普通鋼板，ABH板的隔聲性能更好。

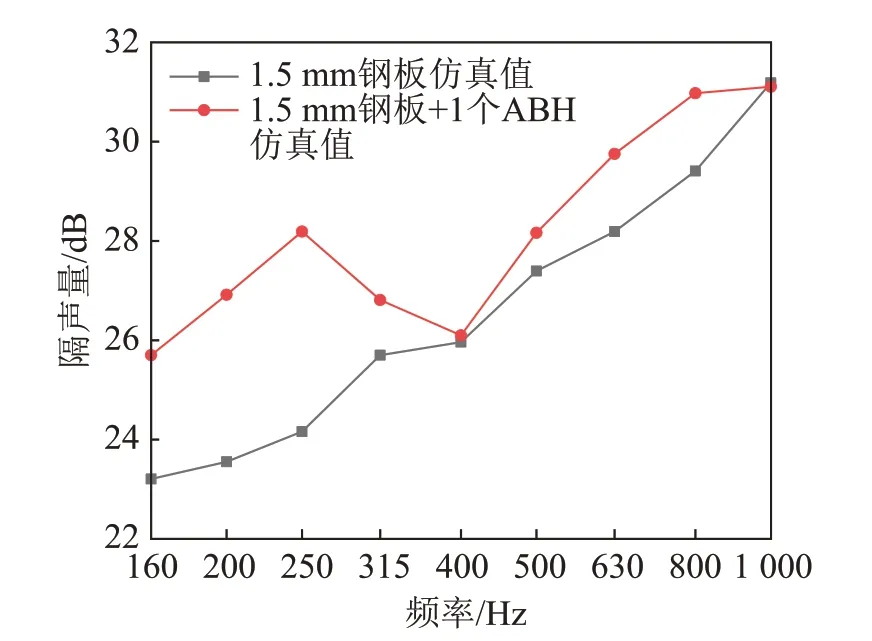
圖7 1.5 mm鋼板與1.5 mm ABH板隔聲量對比圖Fig.7 Comparison of STLs between 1.5 mm steel plate and 1.5 mm AHB steel plate

3 聲學黑洞復合隔聲結構隔聲性能影響因素分析

3.1 聲學黑洞復合隔聲結構隔聲量分析

在保持復合隔聲結構主要尺寸不變的基礎上，在隔聲板中心位置添加一個黑洞結構。黑洞結構的半徑為50 mm，冪指數m=2，截斷厚度為0.5 mm，則黑洞中心剖面的厚度表達式為h(x)=0.4x2+0.5。黑洞復合隔聲結構如圖8所示。

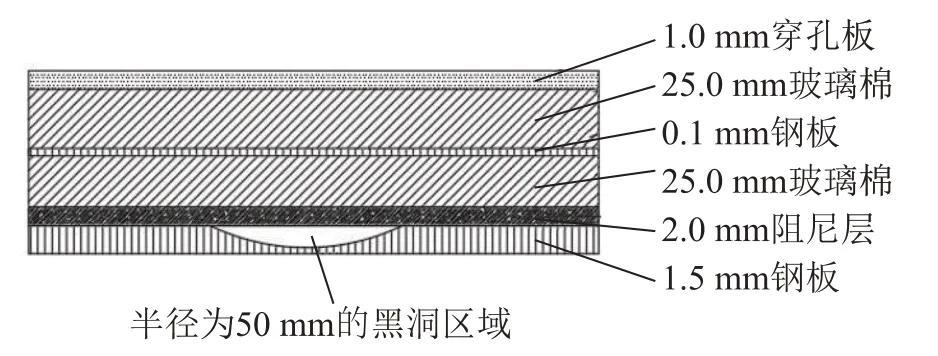
圖8 黑洞復合隔聲結構Fig.8 Composite sound insulation structure with ABH

復合隔聲結構采用六面體單元劃分，且滿足每個單位波長至少包含6個單元的原則。將黑洞薄板結構沿板厚方向劃分為3層網格，其中厚度均勻區域最大單元的邊長為8.71 mm，黑洞區域最大單元的邊長為4.91 mm。復合隔聲結構的隔聲量計算結果如圖9所示。

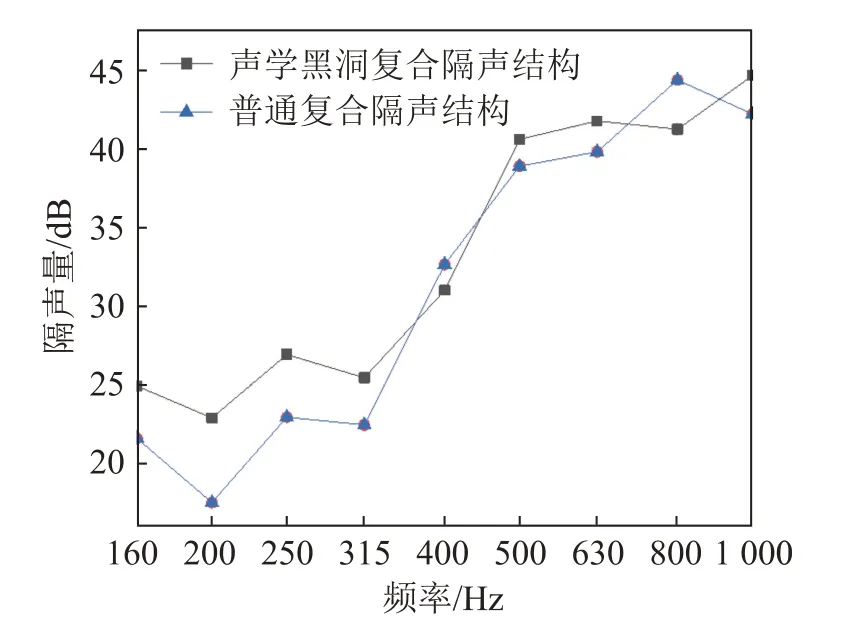
圖9 復合隔聲結構與聲學黑洞復合結構隔聲量對比Fig.9 Comparison of STLs between the normal and the ABH based composite sound insulation structure

由圖9可知：在160～1 000 Hz頻率范圍內，聲學黑洞復合隔聲結構的隔聲性能明顯優于普通復合隔聲結構。其中在160～315 Hz 頻率范圍內，聲學黑洞每個頻點處的隔聲量比普通復合結構高2.9 dB以上。在整個分析頻段內，聲學黑洞復合隔聲結構相比復合隔聲結構，隔聲量平均提高了1.9 dB。因此，聲學黑洞能改善復合隔聲結構中低頻段的隔聲性能。

3.2 阻尼對隔聲性能的影響

在ABH 區域粘貼阻尼可顯著改善截斷厚度對彎曲波聚集的不利影響，阻尼材料參數如表3 所示。粘貼阻尼結構的鋼板示意圖如圖10 所示。在不改變材料參數的條件下，研究了敷設黏彈性阻尼材料對黑洞復合隔聲結構的隔聲性能影響，結果如圖11所示。

表3 阻尼層材料參數Table 3 Material parameters of damping layer

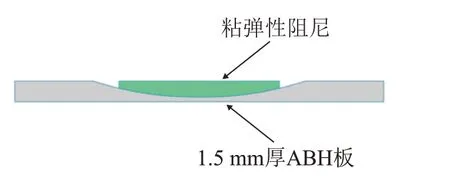
圖10 帶阻尼層的AHB板Fig.10 ABH plate with a damping layer

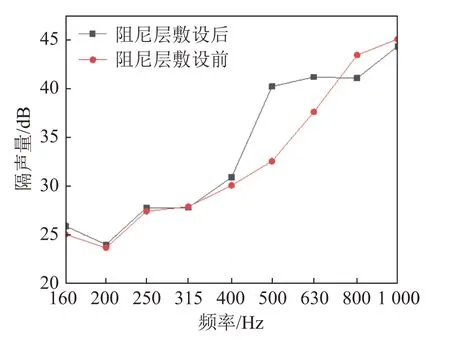
圖11 敷設阻尼層對黑洞板隔聲量的影響Fig.11 Effect of pasting a damping layer on STL of the ABH plate

由圖11 可知：在160～1 000 Hz 頻段范圍內，阻尼層對復合ABH 板結構的隔聲量影響主要集中在中高頻區域。在400～1 000 Hz頻率范圍內，敷設阻尼層后平均隔聲量增加了3.1 dB。

3.3 黑洞數量對隔聲性能的影響

在其他參數不變的條件下，研究聲學黑洞的價目數對聲學黑洞復合隔聲結構隔聲量的影響。黑洞的個數及排列方式如圖12 所示，仿真結果如圖13所示。

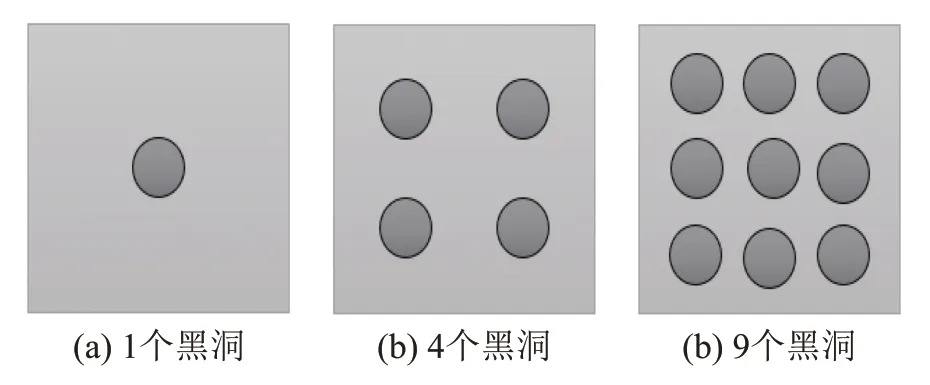
圖12 不同個數的黑洞及排列方式Fig.12 Different numbers of black holes and their arrangements

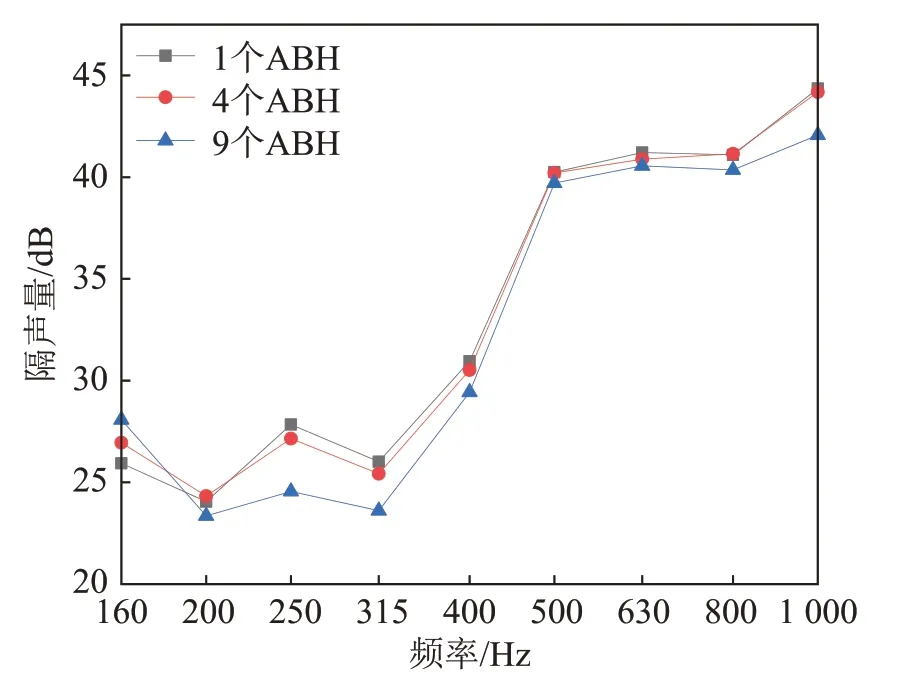
圖13 黑洞個數對復合隔聲結構隔聲量的影響Fig.13 Effect of the number of ABH on STL of the structure

由圖13 可知：在160～1 000 Hz 頻率范圍內，增加ABH 數量并不能提高結構的隔聲量，反而會降低其隔聲量。在此頻率范圍內，結構傳遞損失受勁度控制，增加ABH 的個數會降低結構的剛度。在不同頻段內，每個聲學黑洞的能量聚集效應表現出明顯的差異，嵌有單個AHB的復合結構在160～1 000 Hz頻率范圍內均具有較好的隔聲效果。

3.4 黑洞半徑對隔聲性能的影響

在聲學黑洞個數為1、其他參數不變時，研究聲學黑洞半徑對復合結構隔聲性能的影響。黑洞半徑分別為0.05、0.08、0.12、0.15、0.18 m，仿真結果如圖14所示。由圖14可知：在160～315 Hz頻段內，當半徑為0.05 m和0.08 m時，其隔聲效果較為接近，當黑洞半徑繼續增大后，隔聲效果略有下降，但隨著半徑增加趨于穩定。在500～1 000 Hz頻段內，聲學黑洞半徑每增加0.03 m，平均隔聲量增加0.8 dB以上。

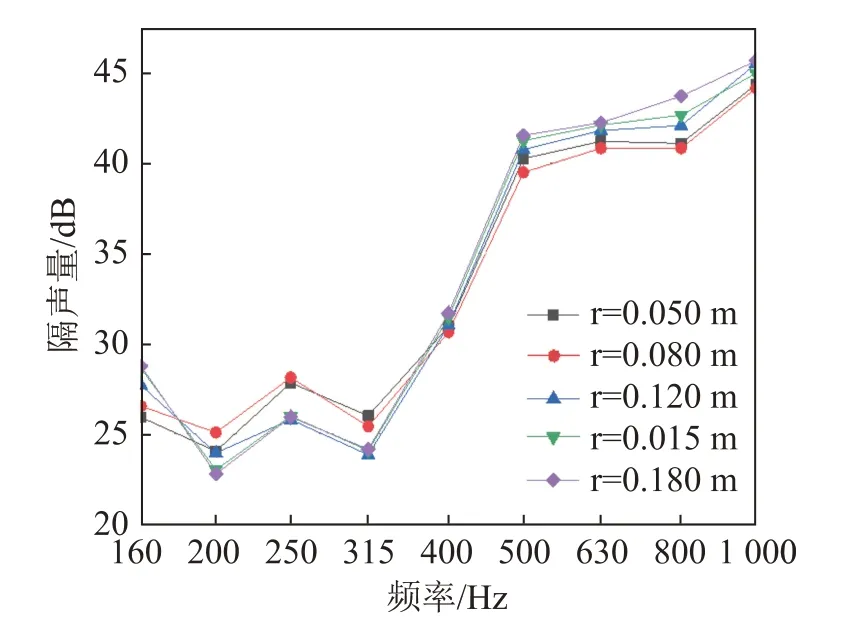
圖14 黑洞半徑對復合隔聲結構隔聲量的影響Fig.14 Effect of ABH radius on STL of the structure

4 結 論

本文研究了聲學黑洞復合隔聲結構的聲學特性。建立了復合隔聲結構的聲學仿真模型，并進行了試驗驗證。進一步研究聲學黑洞復合隔聲板與普通復合隔聲板的隔聲量，通過對比發現，聲學黑洞復合隔聲板對提升隔聲量有顯著效果。最后，通過研究聲學黑洞復合隔聲結構的阻尼層、聲學黑洞數量以及聲學黑洞半徑對隔聲量的影響，得到以下結論：

(1) 在160～1 000 Hz 頻段內，聲學黑洞復合隔聲結構的隔聲量比普通復合隔聲結構的隔聲量平均增加了1.9 dB。

(2) 在聲學黑洞復合隔聲結構的黑洞結構中敷設黏彈性阻尼材料，在400～1 000 Hz 頻率范圍內，隔聲量平均增加了3.1 dB。

(3) 聲學黑洞數量的增加并不能提升復合隔聲結構的隔聲量。在實際應用中，嵌入單個ABH 即可達到較好的隔聲效果。

(4) 在500～1 000 Hz 頻段內，聲學黑洞半徑每增加0.03 m，平均隔聲量增加0.8 dB。