深海低聲速沉積層簡正波用于海底參數反演?
曹景普 周士弘 戚聿波 杜淑媛 彭朝暉
(1 中國科學院聲學研究所 聲場聲信息國家重點實驗室 北京 100190)
(2 中國科學院大學 北京 100049)
0 引言
在我國南中國海北部大陸坡和深海盆地等區域,海底表面廣泛存在著由較軟的沉積物組成的沉積層,該沉積層內的縱波聲速小于底部海水聲速,稱之為低聲速沉積層[1]。低聲速沉積層中沉積物的聲學參數對聲波的傳播損失、到達結構和波形變化都起著關鍵作用,進而影響聲場準確預報、聲源定位結果、聲吶作用距離估算及水聲通信等。因此,深海低聲速沉積層海底參數的獲取對推動我國深海探測研究以及深海海底沉積物中聲波傳播機理研究具有重要的科學價值。獲取海底底質參數的方法包括直接測量法和間接測量法兩種,其中以地聲參數反演為代表的間接測量方法能夠快速低成本獲取局部海域的等效海底參數,一直是水聲領域的研究熱點之一。
國內外關于低聲速沉積層中聲傳播特性及其地聲參數反演的研究雖然不多,但發展特別早。早在1948 年,Press 等[2]總結了海底存在低聲速沉積層的實例,并利用簡正波理論分析了包含低聲速沉積層時3 層均勻液態模型的本征方程及頻散曲線圖。1980年,Rubano[3]基于4 層均勻液態淺海模型分析了海底存在低聲速沉積層時前兩階簡正波的群速度頻散曲線、特征函數和傳播損失,發現低聲速沉積層的存在會造成高頻信號衰減,并反演得到了Corpus Christi沿岸的地聲參數。Hastrup[4]闡述并解釋了淺海環境下聲波在小掠射角入射低聲速沉積層時海底反射損失出現的周期增大現象。李夢竹等[5]在Hastrup 基礎上推導出小掠射角條件下傳播損失周期性增大的頻率間隔與低聲速沉積層參數之間的解析表達式,并將之作為約束條件,提出一種低聲速層海底的地聲參數聯合反演方法。
2017年春季,國外多家研究機構在新英格蘭海域聯合開展了一系列泥底特征實驗[6],其目的是研究聲波在低聲速淤泥層中傳播的物理機制,并驗證一些地聲模型及其反演算法。基于這次實驗,眾多學者分別利用簡正波頻散特征[7-8]、廣角寬帶反射數據[9]、寬帶環境噪聲垂直相關性[10]、多途到達時間[11]等物理量反演了低聲速淤泥層的地聲參數。
上述關于低聲速沉積層傳播特性與地聲參數反演的研究是在淺海環境下進行的,現有的深海地聲參數反演研究通常基于全波場理論,未考慮不同模態傳播特性的差異,具有計算量大的問題。此外,無論是淺海環境還是深海環境,現有的地聲參數反演方法普遍存在多值性和需要準確的水層環境參數等問題,因此研究水層環境參數的影響以及解決多值現象是地聲參數反演亟需解決的問題。
在2018 年5 月南中國海北部大陸坡海域開展的一次海上實驗中,Cao等[12]在坐底式水聽器接收的沉底彈信號中可以觀察到一種具有特殊頻散特征的到達結構,具體表現為低頻成分先到、高頻成分后至,具有較高的截止頻率,稱之為沉積層傳播信號。經研究表明,沉積層傳播信號只有在海底存在低聲速沉積層且近海底收發時才會被觀測到,由被限制在沉積層中傳播的簡正波組成。這類簡正波的激發頻率和頻散特性與沉積層參數密切相關,被稱為沉積層簡正波[12-13]。本文基于簡正波理論和雙層均勻液態海底模型,研究了等聲速水層環境和實測水文環境下沉積層簡正波的頻散特性,提出一種深海低聲速沉積層海底的地聲參數反演方法,并用2018 年南中國海北部大陸坡實驗數據進行了實驗驗證與反演,給出了低聲速沉積層海底的厚度、聲速和密度參數。
1 沉積層簡正波基本理論與頻散特性分析
1.1 3層均勻介質模型的頻散方程
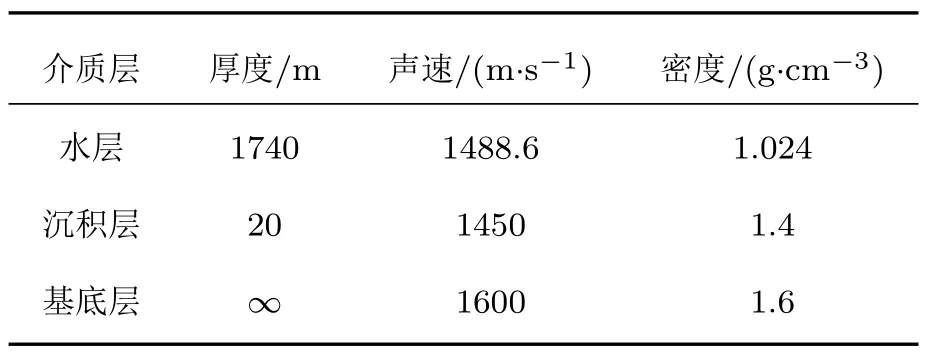
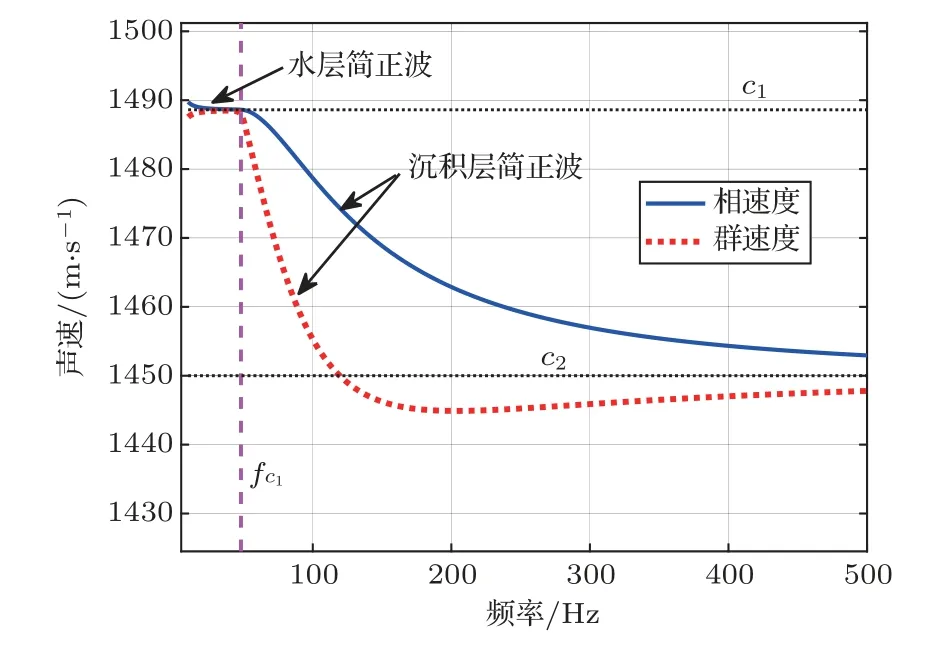
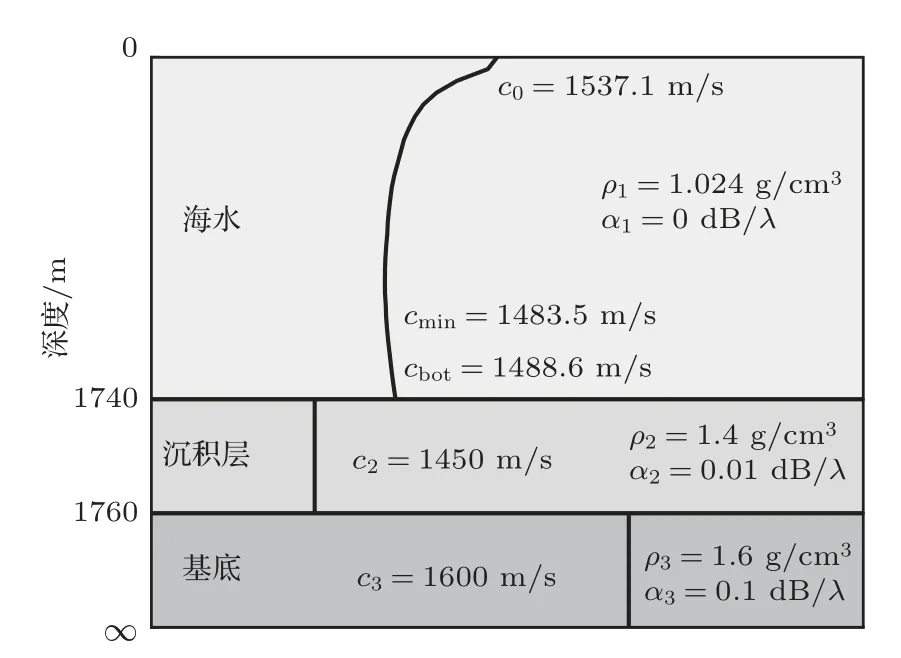
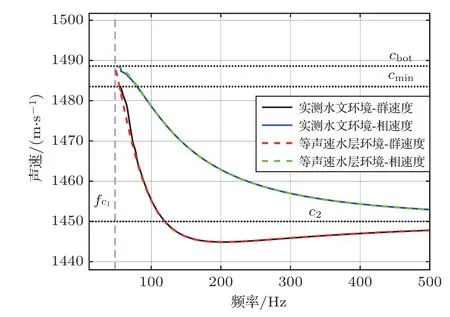
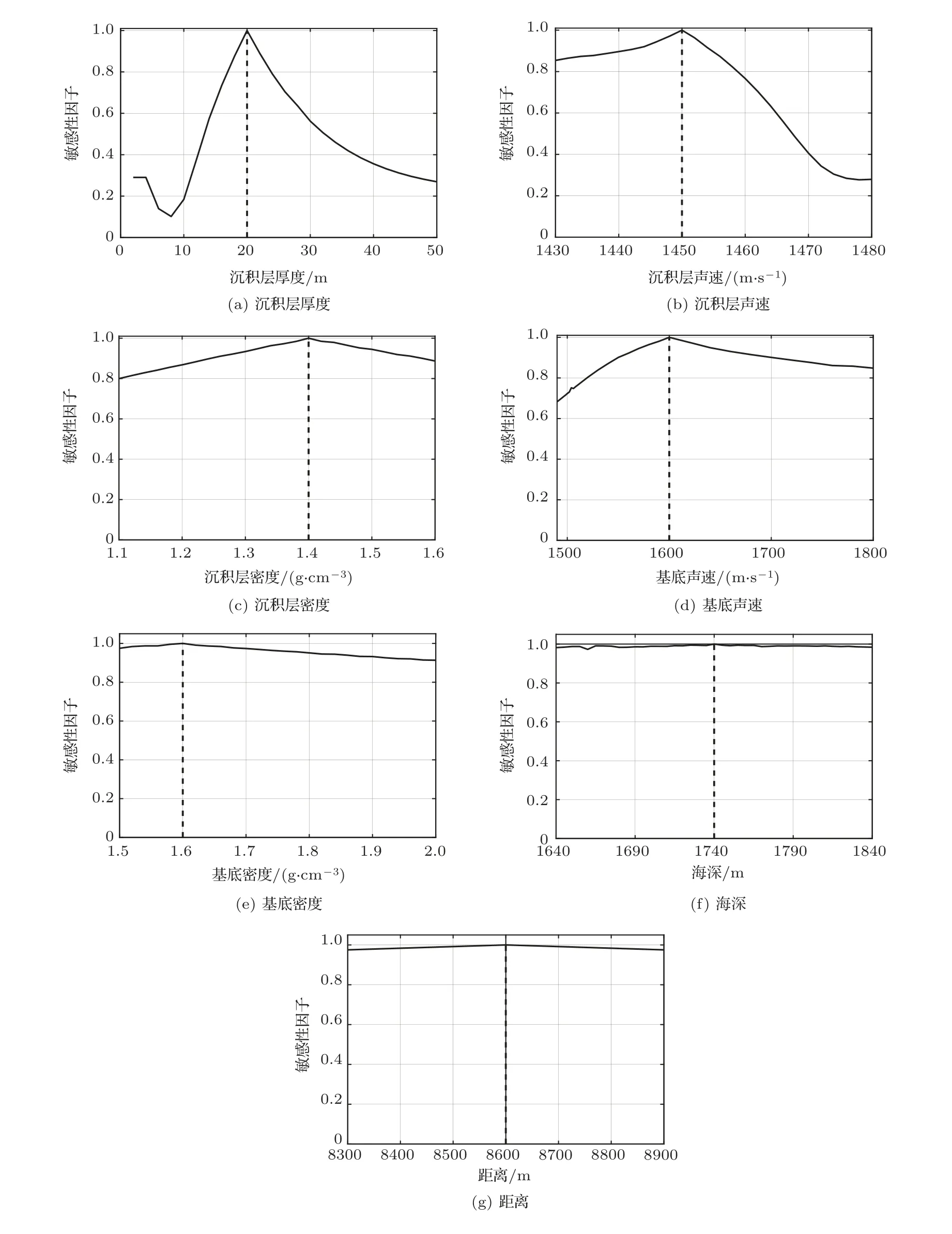
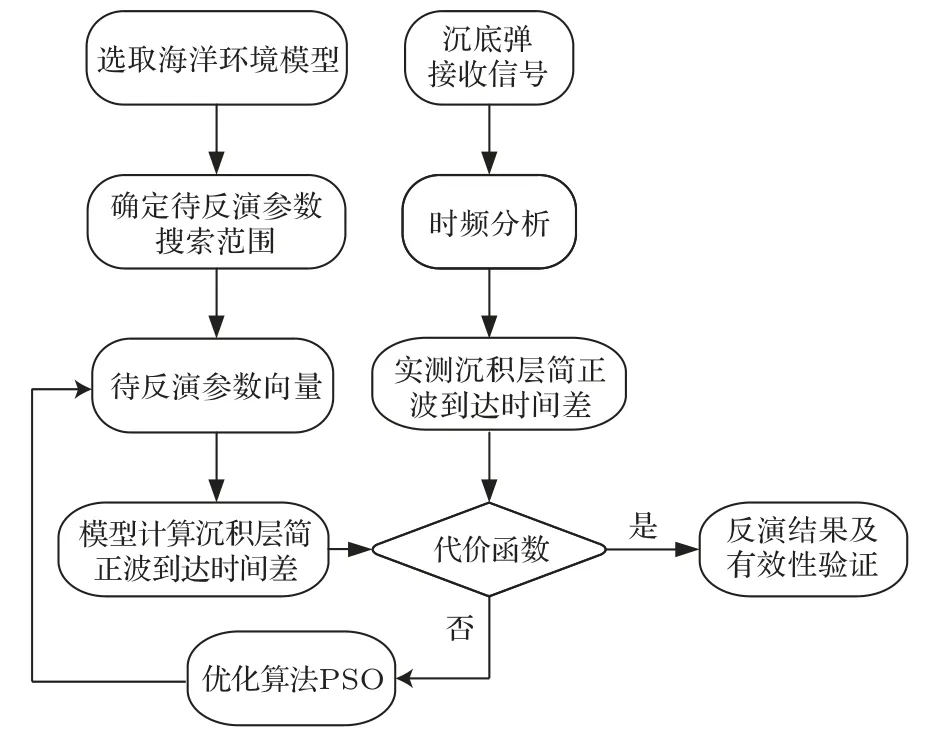
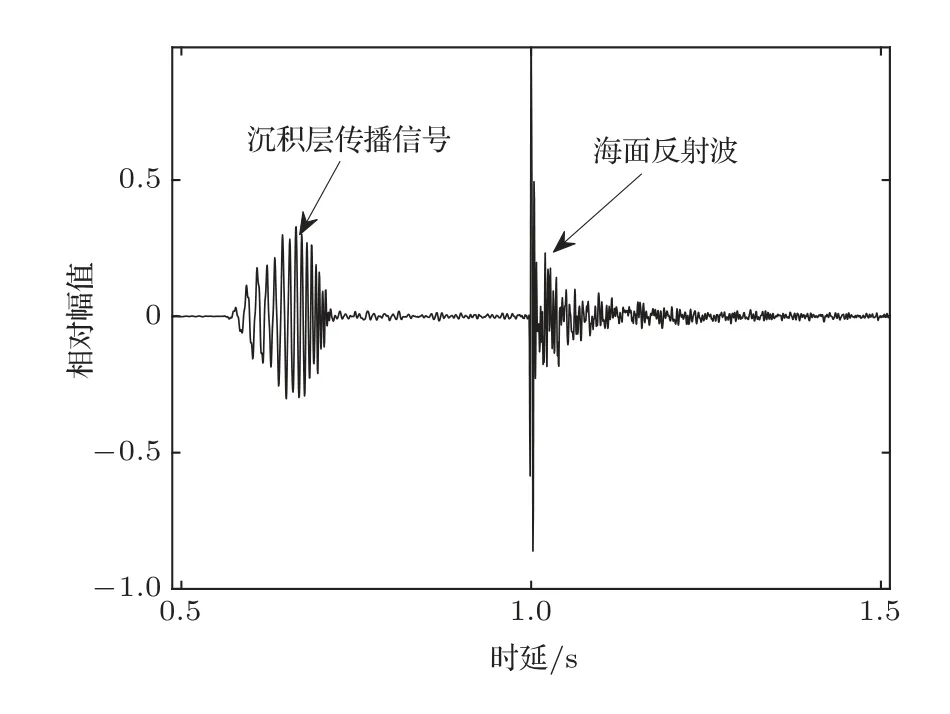
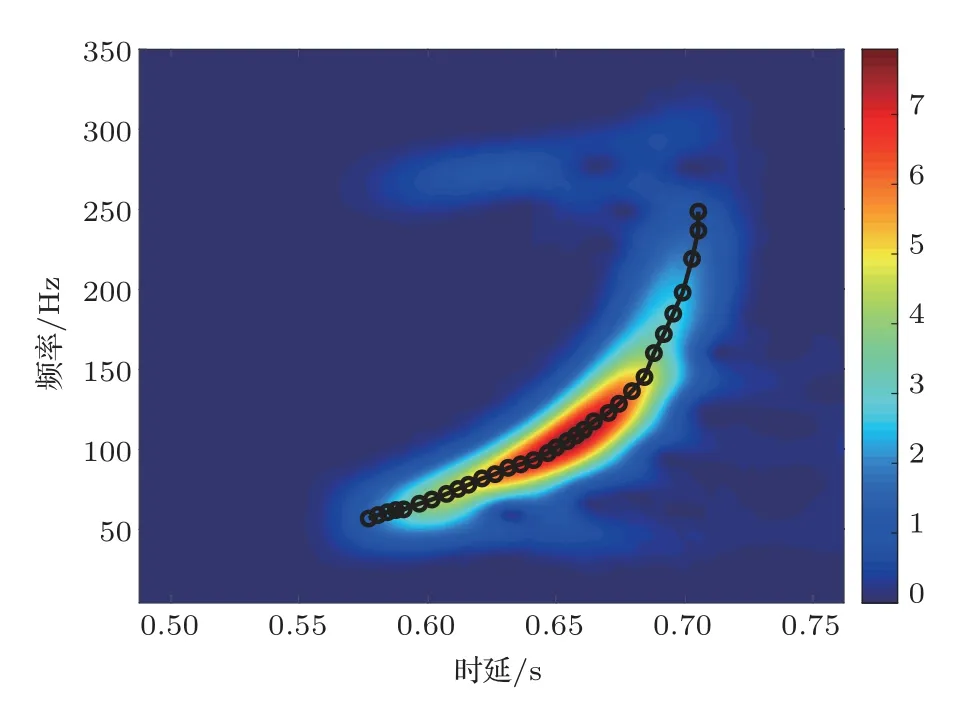
考慮如圖1 所示的3 層均勻液態介質模型,這3 層介質分別為海水層、沉積層和半無限基底層。其中,ci、ρi分別為各層介質的聲速和密度,其中i=1,2,3。H為海深,d是沉積層厚度。各層介質的聲速滿足c2 在分層介質中,根據積分變換法,總聲場的積分表達式可以表示為僅含漢克爾函數的積分[14]: 其中,核函數ψ(kr,z)是與深度有關的格林函數同深度分離的波動方程的齊次解的疊加: 假定一個強度為Sw時間關系為e-iωt的聲源在海水中位于深度zs處,此時圖1 所示模型下漢克爾變換的核函數為 根據海面處聲壓為0、界面處質點位移和聲壓連續的邊界條件,聯立可得以下方程組: 進而可得到幅度齊次解的矩陣方程: 矩陣方程(5)的解對于使系數矩陣的行列式為0的那些水平波數值具有極點。系數矩陣行列式為 其中,m1=ρ2/ρ1,m2=ρ3/ρ1,x=kz,1H,y=kz,2d。 令系數矩陣行列式等于0,可得3層均勻介質波導的特征方程,即頻散方程: 在圖1 所示模型下,水層波數k1、沉積層波數k2和基底波數k3的大小關系為k3 由沉積層簡正波定義可知,該類型簡正波只有在沉積層聲速低于水層聲速時才會被激發。根據波束位移射線簡正波理論可求解出第m階沉積層簡正波截止頻率近似表達式[12]: 從表達式(8)中可以看出,沉積層簡正波截止頻率與沉積層厚度d成反比,與聲速比(c2/c1)呈正相關關系,即沉積層越厚,聲速比越小,越容易激發沉積層簡正波。 考慮如表1所示的具體算例,海深H為1740 m,與海上實驗時實測海深相同,水層聲速c1設為1488.6 m/s,與實測聲速剖面的底部海水聲速相同。將各層參數值代入方程(7)中進行求解即可得到各階簡正波的本征值和頻散曲線。 表1 3 層均勻介質模型參數Table 1 Parameters of the three-layer homogeneous model 圖2 給出了表1 所示模型參數下解頻散方程(7)得到的10~500 Hz 頻段內第一階簡正波頻散曲線,并標記了由表達式(8)計算的截止頻率fc1,其中低于截止頻率的部分屬于水層簡正波,高于截止頻率的部分屬于沉積層簡正波。從圖2 中可以看出,水層簡正波的相速度和群速度隨著頻率增加趨向水層聲速,而沉積層簡正波的相速度和群速度在截止頻率處為水層聲速,隨著頻率增加逐漸趨向沉積層聲速,其中相速度呈單調遞減趨勢,而群速度先減小,后緩慢增大,存在一個最小值,即Airy 相速度。 圖2 表1 所示的模型參數下第一階簡正波頻散曲線Fig.2 The dispersion curves of mode 1 under the model shown in Table 1 考慮如圖3 所示的深海環境模型,水層為實測聲速剖面,存在兩個關鍵聲速:一個是聲速最小值即聲道軸聲速1483.5 m/s,另一個是底部海水聲速1488.6 m/s。圖4 對比了圖3 和表1 所示模型下沉積層第一階簡正波的群速度和相速度曲線,其中表1 所示模型為等聲速水層環境,水層聲速為1488.6 m/s,其頻散曲線(紅色和綠色虛線)通過解頻散方程(7)得到;圖3 所示模型為實測水文環境,其頻散曲線(黑色和藍色實線)由簡正波模型Kraken[15]計算得到。從圖4中可以看出,兩種水文環境下沉積層第一階簡正波的群速度曲線在截止頻率附近存在一些差異,主要表現為等聲速水層環境下的群速度趨向1488.6 m/s,而實測水文環境下的群速度趨向聲道軸聲速1483.5 m/s。除此之外,兩種水文環境下沉積層第一階簡正波的相速度和群速度曲線基本一致。因此如果不考慮截止頻率附近頻段的影響,將水層設為等聲速,且聲速值等于實測底部海水聲速1488.6 m/s,可得到與圖3 所示實測水文環境下基本一致的沉積層第一階簡正波頻散曲線。Cao等[12]研究表明,沉積層第一階簡正波在截止頻率附近處的能量比較弱,因此不考慮截止頻率附近頻段的影響是合理的。 圖3 包含低聲速沉積層和實測海水聲速剖面的3層環境模型Fig.3 A three-layer model including low-speed sediment and the measured water SSP 圖4 圖3 與表1 所示模型下沉積層第一階簡正波頻散曲線的對比Fig.4 Comparison of the dispersion curves of the first order sediment borne mode under the models shown in Fig.3 and Table 1 在實際海洋環境中,低聲速沉積層的厚度通常不會太大,這就導致沉積層簡正波的截止頻率比較高。當聲源和接收器位置都在海底附近時,由沉積層簡正波頻散特性曲線,可以觀察到接收信號中低頻成分先到而高頻成分后到的沉積層傳播信號時域波形(見圖7)。由于沉積層傳播信號被限制在低聲速沉積層中進行傳播,隨距離的衰減要高于海面反射波等水中聲波,尤其是頻率較高時,衰減更為迅速,因此實際接收的沉積層傳播信號中主要以第一階沉積層簡正波為主。從沉積層傳播信號時頻圖中可以直接提取第一階沉積層簡正波的群延時,進而可用于低聲速沉積層海底的地聲參數反演。 當使用單個聲源和單個接收器進行模態反演時,對于一個給定的距離r,不同頻率同一階沉積層簡正波的到達時間差?Tn(f)表示為 其中,n表示沉積層簡正波階數,這里主要考慮n=1 的情況;Vg表示沉積層簡正波的群速度,f表示沉積層簡正波的頻率,fH為參考頻率。 實驗的沉積層傳播信號是一種時頻分布聚集性較高的寬帶信號,其群延時曲線一般是和其時頻分布的峰值曲線位置重合,可以從高分辨的時頻表示的峰值位置直接得到沉積層簡正波的群延時曲線,然后得到實驗數據的沉積層簡正波到達時間差。對于實驗的沉積層傳播信號而言,短時傅里葉變換(Short-time Fourier transform,STFT)[16]的時頻分辨率足以滿足要求。 其中,fi表示反演過程中所使用的不同頻率,N是用于反演的頻點個數,m是包含待反演參數的向量,對于不同的代價函數,待反演的參數也會不同。該代價函數表征多個頻率下理論計算到達時間差與實驗數據到達時間差的最小均方根誤差,通過對代價函數進行多維尋優計算,就可以得到各個待反演的海底參數。 地聲參數反演中,某個環境參數變化而引起的代價函數的變化稱為參數的敏感性,敏感性強的參數變化能夠引起較強的代價函數的變化,所以利用同一代價函數進行海底參數反演時,敏感性強的參數比敏感性弱的參數能夠被更好地反映出來,取得更好的反演效果。所以各個環境參數的敏感性對于分析待反演參數可靠性方面非常重要。 為了能夠直觀對比各個環境參數的敏感性大小,定義敏感性因子為 其中,m0表示真實模型或參考模型的反演參數向量,m1表示環境參數發生變化后的反演參數向量,max(E(m1)-E(m0))表示所有參數發生變化后引起代價函數變化的最大值。 由敏感性因子的定義可知,當各個反演參數在相應的搜索區間內變化時,會得到各個參數的敏感性曲線。只有當模型計算時利用的環境參數值與真實或參考模型的環境參數值一致時,敏感性因子等于1。對于同一代價函數,環境參數的敏感性曲線越陡峭,峰值越明顯,敏感性因子越小,則該參數的敏感性越強,反之敏感性越弱。 針對低聲速沉積層地聲參數反演時采用了雙層均勻海底模型,地聲參數的參考值如表1 所示,參考距離為8600 m。基于圖3 所示的深海環境模型,Cao 等[13]研究了環境參數對沉積層簡正波群速度的影響,發現近海面聲速剖面的變化對其完全沒有影響,影響最顯著的是沉積層聲速和沉積層厚度。為了直觀對比不同環境參數的敏感性,利用式(10)所示的代價函數計算7 個環境參數的敏感性,得到如圖5所示的7個參數的敏感性曲線圖。圖中,垂直虛線表示各個參數的參考值。由參數的敏感性曲線可知:沉積層厚度和沉積層聲速的敏感性曲線在參考值附近有明顯的峰值,并且敏感性曲線比較陡峭,說明沉積層簡正波到達時間差對這兩個參數比較敏感,將沉積層簡正波到達時間差作為代價函數反演得到這兩個參數的可信度比較高;沉積層密度和基底聲速的敏感性雖然要低于沉積層厚度和沉積層聲速,但仍然不可忽略;而基底密度、海深和距離這3 個參數的敏感性曲線比較平緩,沒有明顯的峰值,說明這3 個參數對沉積層簡正波到達時間差不敏感,因而反演得到的這3個參數可信度不高。 圖5 環境參數的敏感性曲線Fig.5 Sensitivity curves for environmental parameters 根據圖5 所示的環境參數敏感性結果,結合Cao 等[13]的研究,可以發現海深和水層聲速剖面不均勻性對沉積層第一階簡正波的群速度基本沒有影響,而海底沉積層相對水層聲速比值和沉積層厚度對沉積層簡正波群速度的影響非常顯著,因此利用沉積層簡正波到達時間差進行海底參數反演時,可以避免海深和水層環境參數的影響,有效緩解多值問題。此時待反演參數向量可設為m=[d,c2,ρ2,c3],沉積層簡正波頻散曲線計算所需的基底密度ρ3可由Hamilton 經驗公式[17]c3=2330.4-1257.0ρ3+間接獲得。 圖6 給出了利用沉積層簡正波到達時間差反演海底參數的流程圖。首先,對實驗接收信號進行時頻分析,估計沉積層簡正波的相對到達時間,提取沉積層簡正波的到達時間差;其次,選擇表1 所示的海洋環境模型,確定待反演參數及其搜索范圍,理論計算沉積層簡正波的到達時間差;然后,用實測到達時間差與理論計算到達時間差構成代價函數,利用全局優化算法反演出沉積層參數;最后對反演結果進行有效性驗證。 圖6 反演流程圖Fig.6 Flowchart of inversion 實驗于2018 年5 月在南中國海北部大陸坡海域開展,期間在海底放置了接收水聽器,深度約為1740 m,并投擲了一些沉底彈。選擇距離水聽器約8.46 km 的沉底彈進行分析,該沉底彈與水聽器之間的海底地形相對比較平坦。圖3 所示模型中的水層聲速剖面為實驗期間水聽器所在站點實測的聲速剖面,其中聲道軸深度在1130 m,聲道軸聲速為1483.5 m/s,底部海水聲速為1488.6 m/s,海表面聲速為1537.1 m/s,為典型的不完全深海聲道。 圖7 給出了水聽器接收到的信號時域波形,從中可以觀察到先于海面反射波到達的沉積層傳播信號,其時頻圖如圖8 所示。從沉積層傳播信號的時域波形和時頻圖可知,沉底彈經過一定距離傳播后,接收信號在60~220 Hz 頻段內有非常明顯的頻散現象發生,具體表現為低頻成分先到、高頻成分后至,具有較高的截止頻率。此外,沉積層傳播信號能量主要集中在第一階,可以直接在時頻圖上提取第一階沉積層簡正波頻散曲線,如圖8所示,圖中黑色圓圈連線為提取的頻散曲線。提取的沉積層簡正波群延時包含了沉積層參數信息,可用于海底參數反演中。從圖8 中還可以看出,沉積層簡正波在截止頻率附近的能量較弱,可不提取這部分頻段的群延時,然后將水層聲速設為底部海水聲速進行反演,可大大降低反演計算量。 圖7 距離8.46 km 的接收信號時域波形Fig.7 Waveform of the received signal at a distance of 8.46 km 圖8 距離8.46 km 的接收信號時頻圖及提取的群時延Fig.8 Spectrogram and the extracted modal group delays of the received signal at a distance of 8.46 km 采用雙層均勻液態海底模型,并使用粒子群算法[18](Particle swarm optimization,PSO)在參數空間中搜索全局最優解,使式(10)所示的代價函數值達到最小。PSO 算法搜索的參數共4 個,分別為沉積層厚度、沉積層聲速、沉積層密度和基底聲速。根據實測底部水層聲速和歷史經驗信息,待反演參數的搜索邊界如表2 所示。基底密度利用Hamilton經驗公式得到。PSO 算法初始粒子40個,速度范圍為參數范圍的0.2 倍,共迭代300 次,且通過多次平行計算確保算法收斂于全局最優值。 表2 參數空間及反演結果Table 2 Parameters space and inversion results 運用基于不同頻點的沉積層簡正波到達時間差進行海底參數反演的方法,得出實驗海區的反演結果如表2 所示。結合實測聲速剖面,聲速比(c2/c1=1450.0/1488.6)約為0.974。沉積層基底密度通過Hamilton 經驗公式計算得到的結果為1.53 g/cm3。 將得到的反演結果代入模型進行計算,圖9 為由實驗數據提取的沉積層簡正波群時延和模型計算得到的群時延對比圖。從圖中可以看出,根據反演結果代入模型計算的第一階沉積層簡正波群時延與實驗結果在大部分頻率上都符合得很好,只在少數高頻頻點出現了偏離,所以將反演結果作為參數最優值比較可信。 圖9 實驗數據提取與模型計算得到的群時延對比Fig.9 Comparison of the group delays obtained from experimental data and model calculation 在得到反演結果后,接下來的關鍵步驟就是對反演結果進行有效性驗證。最直接檢驗反演結果有效性的方法是將反演結果和海底底質采樣結果進行比較。在2018年5 月的海上實驗中并沒有進行海底采樣,但2014年春季在同一海域進行過海底底質采樣,距離水聽器較近的底質采樣數據表明海底存在低聲速沉積層,2.3 m 采樣深度內的平均聲速約為1447.9 m/s,平均聲速比約為0.972,平均密度約為1.41 g/cm3,與反演結果比較吻合。 由于底質采樣數據并不完善,且可能存在高頻測量誤差的問題,利用統計的方法來描述反演結果是對其可靠性分析的有效工具,其中后驗概率分析是對反演結果在搜索空間中的分布進行概率統計,從而確定反演算法及反演結果的有效性[19-20]。 為了得到反演結果的后驗概率分布,在求解代價函數式(10)的過程中,搜索空間中的所有采樣值Mk及其目標函數值E(Mk)被保存下來,構成模型向量的采樣空間?。對反演結果在采樣空間?中的分布進行概率統計,把向量M按照其代價函數值的大小進行排序,按照Boltzmann分布進行加權,從而得到反演結果的第k組向量后驗概率分布[19]: 其中,Nobs是保存下來的模式向量的個數,T是溫度控制參數。研究[19]表明溫度控制參數T取反演過程中50個最佳的代價函數的均值比較合適,則參數向量M第n個參數的值為m時的邊緣概率密度為 利用邊緣概率分布判斷反演結果好壞是一種很重要且有效的手段。圖10 為反演參數的邊緣概率密度分布圖,其中向上的箭頭所示位置表示通過代價函數反演得到的海底參數所對應的值。由圖可知,沉積層厚度、沉積層聲速和基底聲速這3 個待反演參數的邊緣概率分布比較集中,說明這3 個參數的反演結果可信度比較高;但沉積層密度的邊緣概率分布比較分散,說明其反演結果可信度不是很高。得到的結論和敏感性曲線得到的結論基本一致。 圖10 反演參數的邊緣概率分布Fig.10 The marginal probability distribution of inversion parameters 針對深海低聲速沉積層海底的參數反演問題,推導了3 層均勻介質模型下波導的頻散方程,對比分析了等聲速水層環境和實測水文環境下沉積層簡正波的頻散曲線,發現如果不考慮截止頻率附近頻段,兩種水層環境下的群速度頻散曲線幾乎一致。隨著頻率增加,沉積層簡正波的群速度先減小,后增加,并逐漸趨向沉積層聲速。在此基礎上,提出了一種基于沉積層簡正波到達時間差的深海低聲速海底參數反演方法,并利用2018 年5 月在南中國海北部大陸坡實驗中獲得的60~220 Hz 頻段內的沉底彈信號對實驗海域的海底聲學參數進行了反演,得到沉積層的厚度為16.4 m,聲速為1450.5 m/s,聲速比為0.974,與底質采樣的聲速1447.9 m/s、聲速比0.972 相比,二者比較吻合。相較于以往低聲參數反演方法,本文所提方法充分利用了沉積層簡正波的激發特性和頻散特性,適用于深海低聲速沉積層海底,具有敏感高效、計算量小、受水層環境影響小、僅需要單個水聽器和單個聲源的特點,具備較高的應用價值。但本文方法反演的沉積層海底參數只是基于一次實驗的結果,如何對其進行進一步驗證以及如何提高沉積層密度的反演精度是接下來需要研究的工作。1.2 沉積層簡正波頻散特性分析
2 反演方法與敏感性分析
2.1 代價函數分析
2.2 參數敏感性分析
2.3 反演算法流程
3 實驗數據分析
3.1 沉積層簡正波頻散曲線提取
3.2 海底參數反演

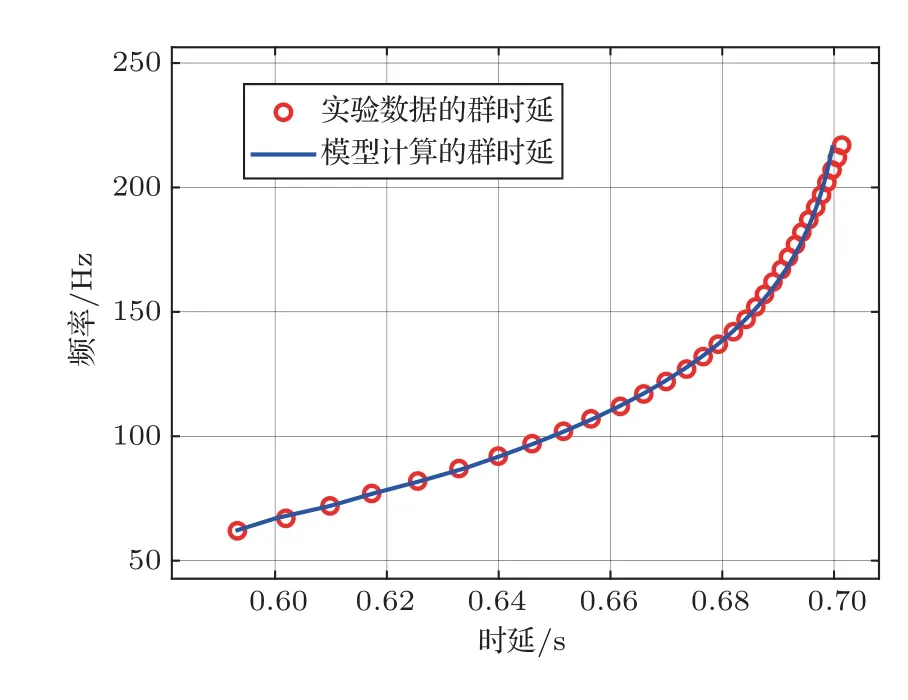
3.3 反演結果的有效性驗證
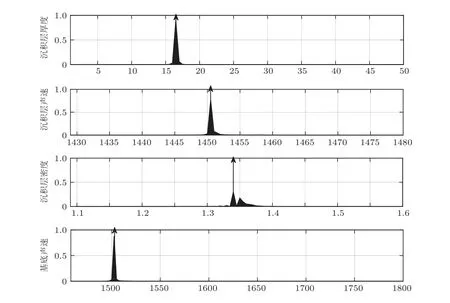
4 結論

