電動水上飛機低噪聲螺旋槳翼型優化?
張 磊 王赫鳴 劉遠強2, 徐 海 王 志
(1 中國民用航空沈陽航空器適航審定中心 沈陽 110043)
(2 遼寧銳翔通用飛機制造有限公司 沈陽 110136)
(3 沈陽航空航天大學航空發動機學院 沈陽 110136)
0 引言
近年來,電動飛機憑借其在環保性、舒適性、維修性和經濟性等方面的優勢,成為航空工業尤其是通用航空未來的重要發展方向[1]。目前,多數電動航空器都選擇效率較高的螺旋槳作為主要拉力裝置為其提供前進的動力。然而,螺旋槳在旋轉過程中對周圍空氣產生持續的擾動,也使螺旋槳噪聲成為了航空器的主要噪聲源。螺旋槳噪聲會產生多方面的危害,如螺旋槳噪聲造成的飛行器機身振動與聲疲勞會影響飛行安全;噪聲傳入機艙,會嚴重影響飛行員的駕駛體驗以及乘客的乘坐體驗;此外螺旋槳產生的噪聲還會對機場及航線周邊環境造成聲污染等[2]。因此有效的螺旋槳降噪技術對于電動飛機未來發展至關重要。
螺旋槳噪聲屬氣動噪聲,由高速旋轉的螺旋槳擾動周圍空氣導致的非定常脈動產生。目前主要的螺旋槳降噪措施有兩種,第一種降噪措施的著眼點是降低聲源強度;第二種是基于破壞性聲波干涉[3]。降低聲源強度的主要方式即對螺旋槳氣動外形進行合理設計,主要通過翼型的設計實現。而相對于重新設計一款翼型,對現有翼型進行優化不失為一種更為高效的方法。目前國內外對于翼型優化的研究工作主要著眼于提升翼型的氣動性能。王清等[4]針對中型運輸直升機翼型進行了優化設計,提出了相適應的目標函數與約束條件,使翼型氣動性能顯著提高。保女子等[5]以升阻比為優化目標,使得變彎度翼型的升阻比提升了22%。熊俊濤等[6]優化設計了跨聲速翼型的氣動性能,使翼型的阻力系數減少了19.34%。而有較少的學者進行了同時考慮聲學性能與氣動性能的翼型優化研究。程江濤等[7]提出以翼型升阻比與噪聲比值(效噪比)作為優化目標的設計方法,并將優化翼型與常用的風力機翼型進行比較,驗證了優化結果。劉雄等[8]以翼型自噪聲作為優化目標、翼型氣動性能作為約束,得到了高氣動性能、低噪聲的風力機專用翼型。李鑫等[9]通過基于噪聲預測模型的翼型氣動優化設計系統,對超臨界翼型進行單點多目標優化設計,顯著提升了翼型在設計狀態下的氣動性能與聲學性能。卓文濤等[10]使用BPM 模型預測風力機翼型氣動噪聲,并使用Powell方法優化設計了NACA0012翼型,使翼型在設計工況下的升阻比提高,噪聲降低。
在翼型優化方法問題上,梯度法是較早被學者們使用的優化方法之一,該方法計算量相對較小,但易陷入局部最優解。因此以遺傳算法為代表的進化類優化算法憑借其魯棒性與全局性逐漸得到了廣泛的應用,但使用進化類算法進行翼型的優化設計存在流場求解次數較多的問題,降低了優化效率。目前國內外學者大部分通過引入代理模型來提高優化效率,如:Kriging 模型[11-12]、響應面模型[13-14]、POD模型[15]等。
本文將對面向通用飛機螺旋槳使用的RAF-6 翼型進行降噪優化,翼型的升、阻力系數及氣動噪聲將通過計算流體動力學(Computational fluid dynamics,CFD)與氣動聲學方程相結合的CFD/FW-H 方法計算得到。將引入響應面模型的遺傳算法作為優化設計方法,型函數的系數作為設計變量,翼型氣動噪聲與升阻比加權組合作為優化目標,保證翼型氣動性能不會過多損失,即翼型升、阻力系數變化不超過10%作為約束,對RAF-6 翼型進行了優化設計,最后將優化翼型與原始翼型進行對比從而驗證優化結果。
1 螺旋槳翼型氣動噪聲計算
1.1 計算方法與理論
本文計算翼型的氣動噪聲使用CFD/FW-H 方法,該方法先對翼型流場進行CFD 計算,再將計算結果代入FW-H方程進行聲場的求解。
首先,使用SSTk-ω湍流模型求解穩態流場,該模型可表示為
其中:Γk與Γω分別為k與ω的有效擴散率;Gk與Gω分別為k與ω的平均速度梯度;Yk與Yω分別為k與ω的耗散;Dω則為交叉擴散項。
當穩態流場達到穩定,以穩態流場計算結果作為初始條件進行非穩態計算,并引入FW-H 方程計算翼型的氣動噪聲。非穩態流場采用大渦模擬湍流模型。
大渦模擬的控制方程為
其中:ρ為流體密度;t為時間;ui與uj為速度分量;xi與xj為位置分量;p為壓力;μ為流體運動黏性系數;亞格子應力,表示被過濾掉的小尺寸漩渦對大尺寸漩渦的影響;對于不可壓縮流體,式(3)為
通過亞格子模型得到被過濾掉的小尺寸漩渦對流場的影響。選擇標準Smagorinsky-Lilly 模型,該模型中,流體運動黏性系數和網格混合長度表示為
其中:k為von Karman 常數;d代表距離最短表面邊界的長度;V為單元體積;Cs為Smagorinsky 常數,取0.1。
FW-H 方程為聲比擬方法的通用形式,該方程可寫為
式(7)中:α0為遠場聲速;p′為觀測點的聲壓;ui與un分別為xi方向與垂直于聲源面方向的流體速度分量;vi與vn分別為xi方向與垂直于聲源面方向的聲源面速度分量,聲源面為f=0;Pij為應力張量;Tij為Lighthill 張量;δ(f)與H(f)分別為Dirac函數與Heaviside函數。
1.2 計算模型及結果
表1 列出了兩種工況[16-17],以這兩種工況為算例分別驗證本文計算方法對翼型氣動特性與氣動噪聲計算的準確性。
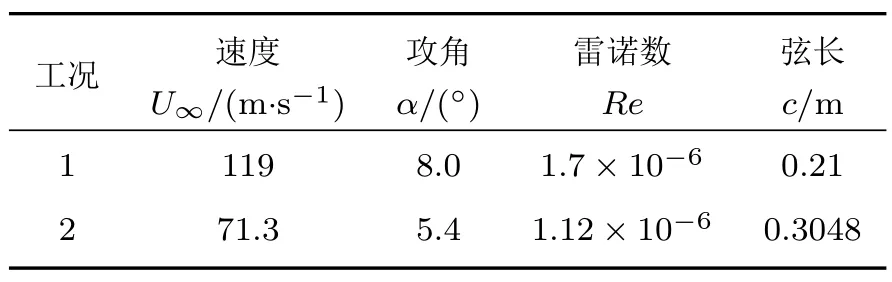
表1 算例計算工況Table 1 Computing conditions of examples
計算通過商業軟件Fluent 實現,計算域遠場取10c,其中c為翼型弦長。為計算翼型氣動噪聲,如圖1 所示,在距翼型中心10c的圓周上布置36 個噪聲接收點。圖2 為翼型附近區域的網格,靠近壁面的網格做加密處理,第一層網格高度滿足y+<1。定義流場內流體為理想氣體,邊界為壓力遠場,采用SIMPLEC 算法,使用耦合求解器、二階迎風離散格式求解,按1.1 節所述流程,首先采用SSTk-ω湍流模型進行穩態計算,待流場穩定后使用大渦模擬模型進行非穩態計算,亞格子模型選擇Smagorinsky-Lilly 模型,時間步長?t=8.3×10-5s,計算5000步,計算物理時間0.4 s。引入FW-H方程計算噪聲,源相關長度取5c。
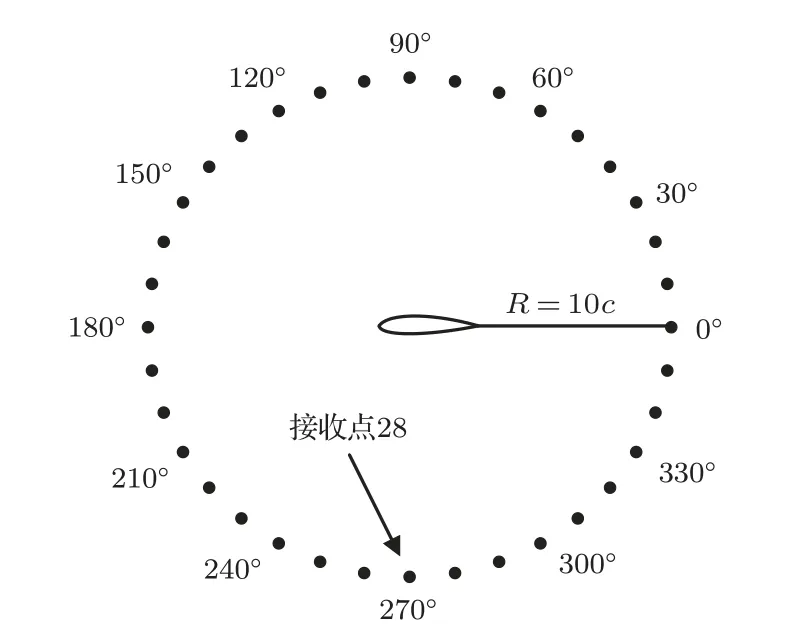
圖1 噪聲接收點分布Fig.1 Layout of noise receivers
圖3 為網格無關性驗證。圖中數據為翼型升阻力系數隨網格數量變化的相對值,當網格數量在25×104~32×104時,翼型的升、阻力系數已無明顯變化,證明計算結果已與網格數量無關,因此后續計算網格數將保持在28×104左右。由圖4 可以看出本文計算結果與試驗結果吻合較好,由此,本文所使用的計算方法的準確性得以驗證。
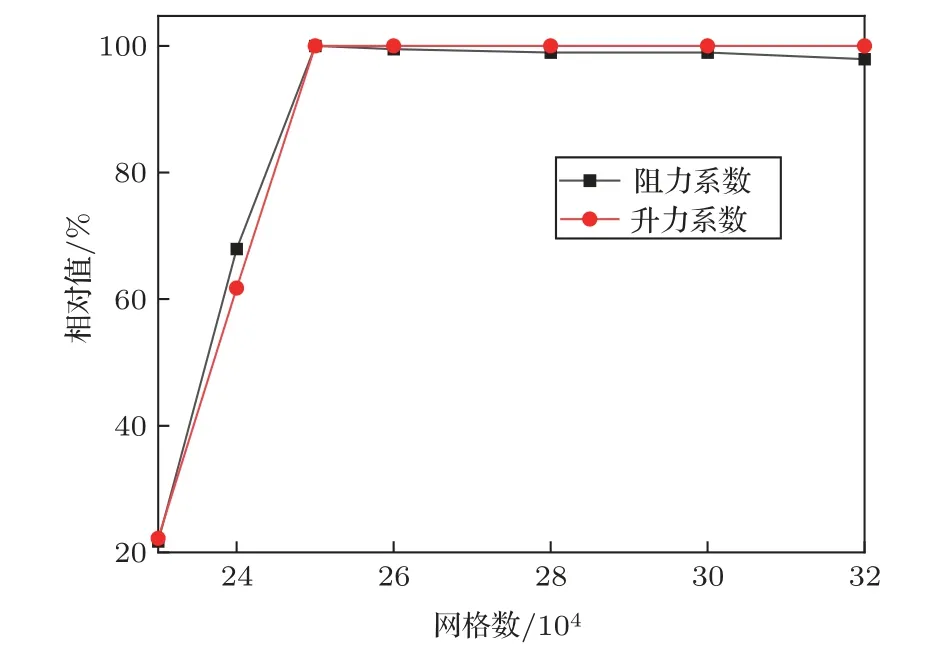
圖3 網格無關性驗證Fig.3 Grid independence verification
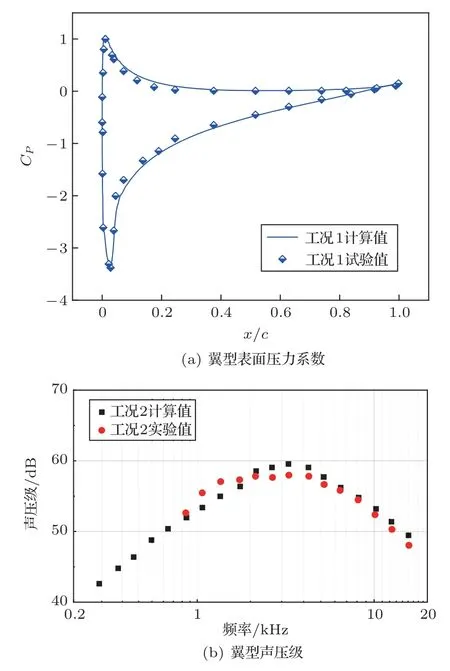
圖4 計算值與試驗值對比Fig.4 Comparison of calculation and experiment
2 翼型的幾何表達及設計變量
對翼型進行優化設計就是通過選取相應的變量,并對變量取不同的值,而后經過計算得到變量取不同值時對應的結果,從而得到令結果最優的變量取值的過程。這些變量往往是翼型的幾何參數,因此需要對翼型進行幾何形式的表達,從而實現變量的改變。本文所使用的幾何表達方式是將幾何擾動加載到基準翼型上,幾何擾動是由一定數量的型函數線性疊加而成。式(8)為翼型的幾何表達式。
式(8)中:fnew(x)為新翼型的表面坐標函數;f0(x)為基準翼型的表面坐標函數;n為疊加型函數的個數;ck為所疊加型函數的系數,即為本文所使用的變量。
fk(x)即為型函數,可表示為
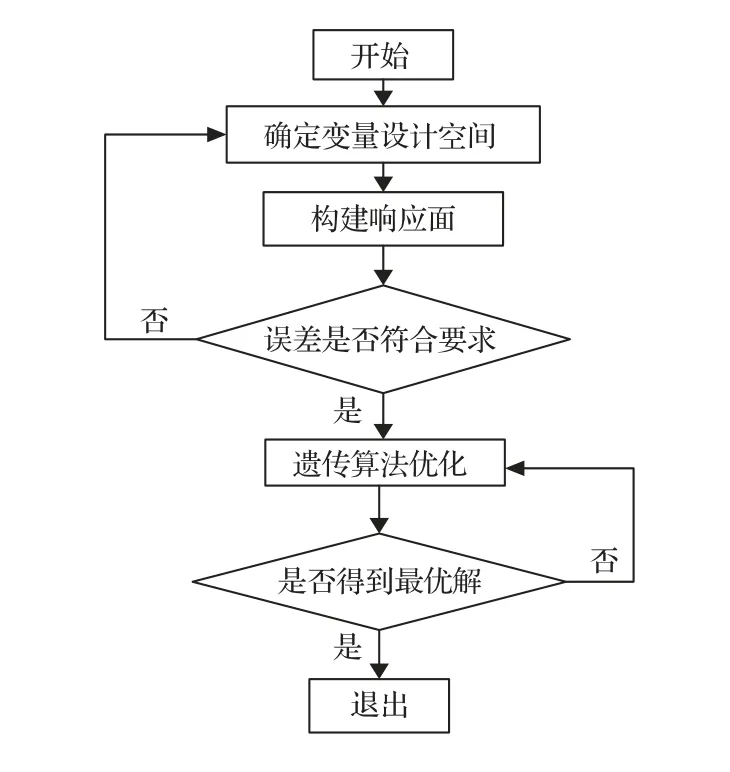
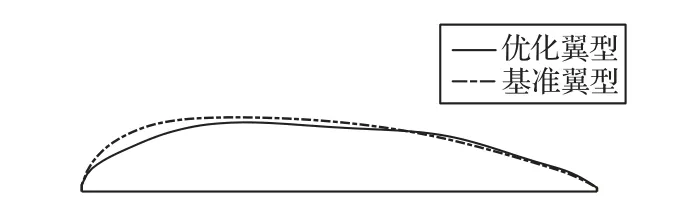
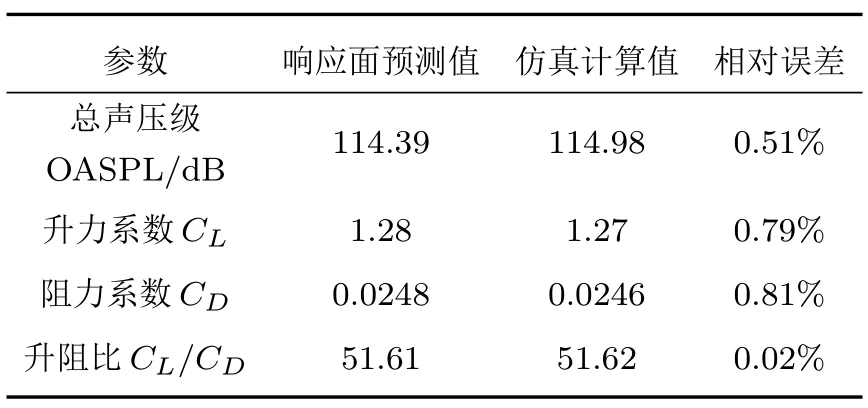
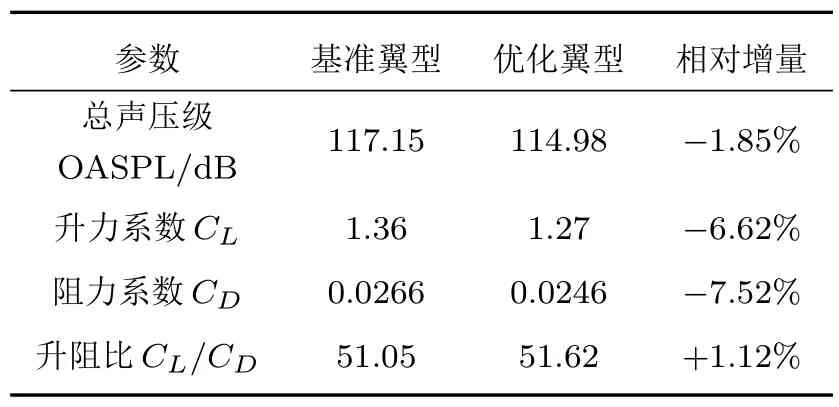
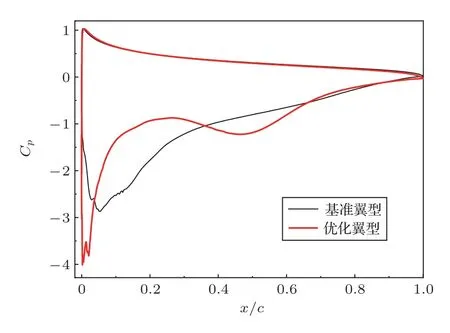
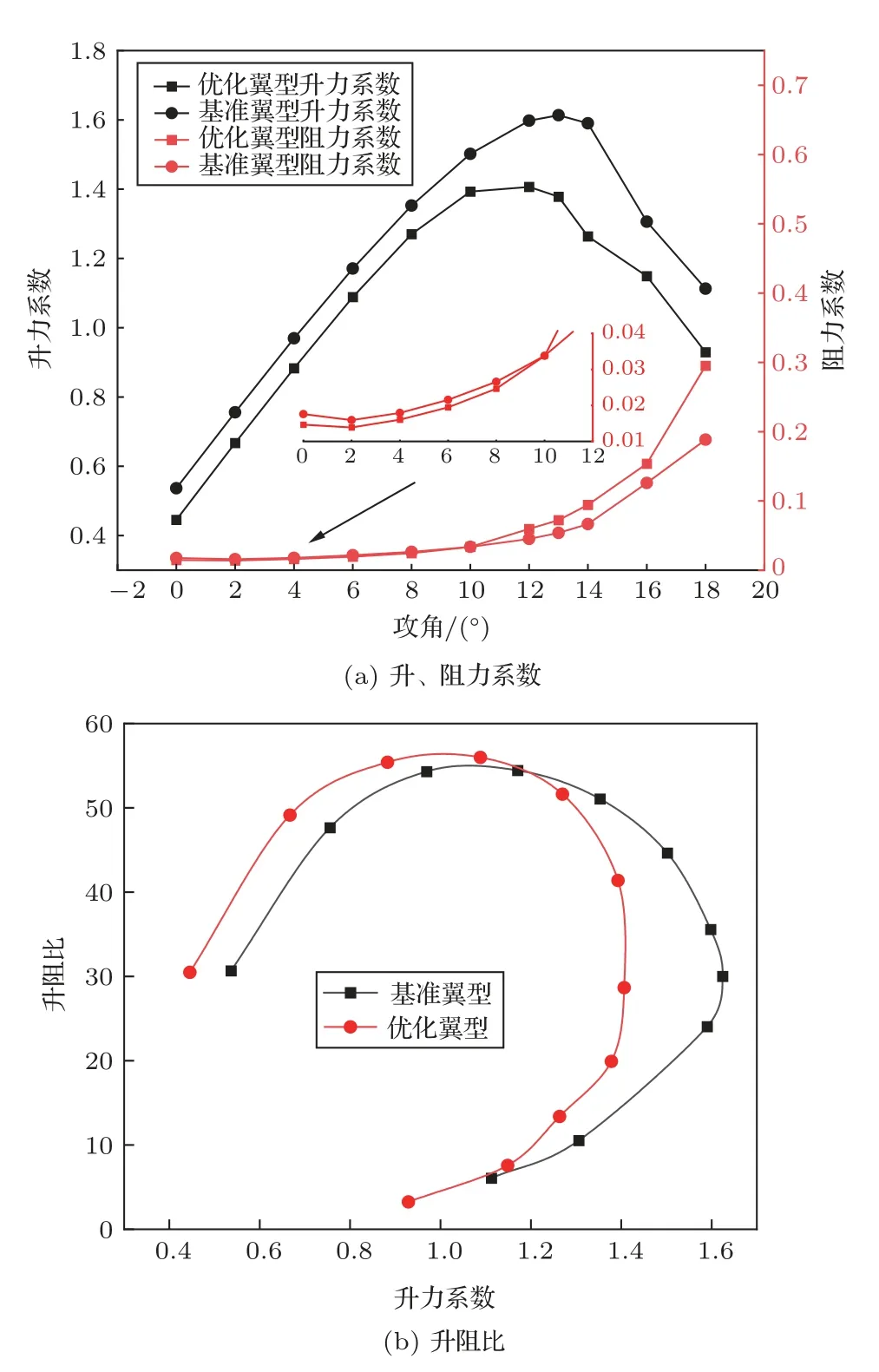
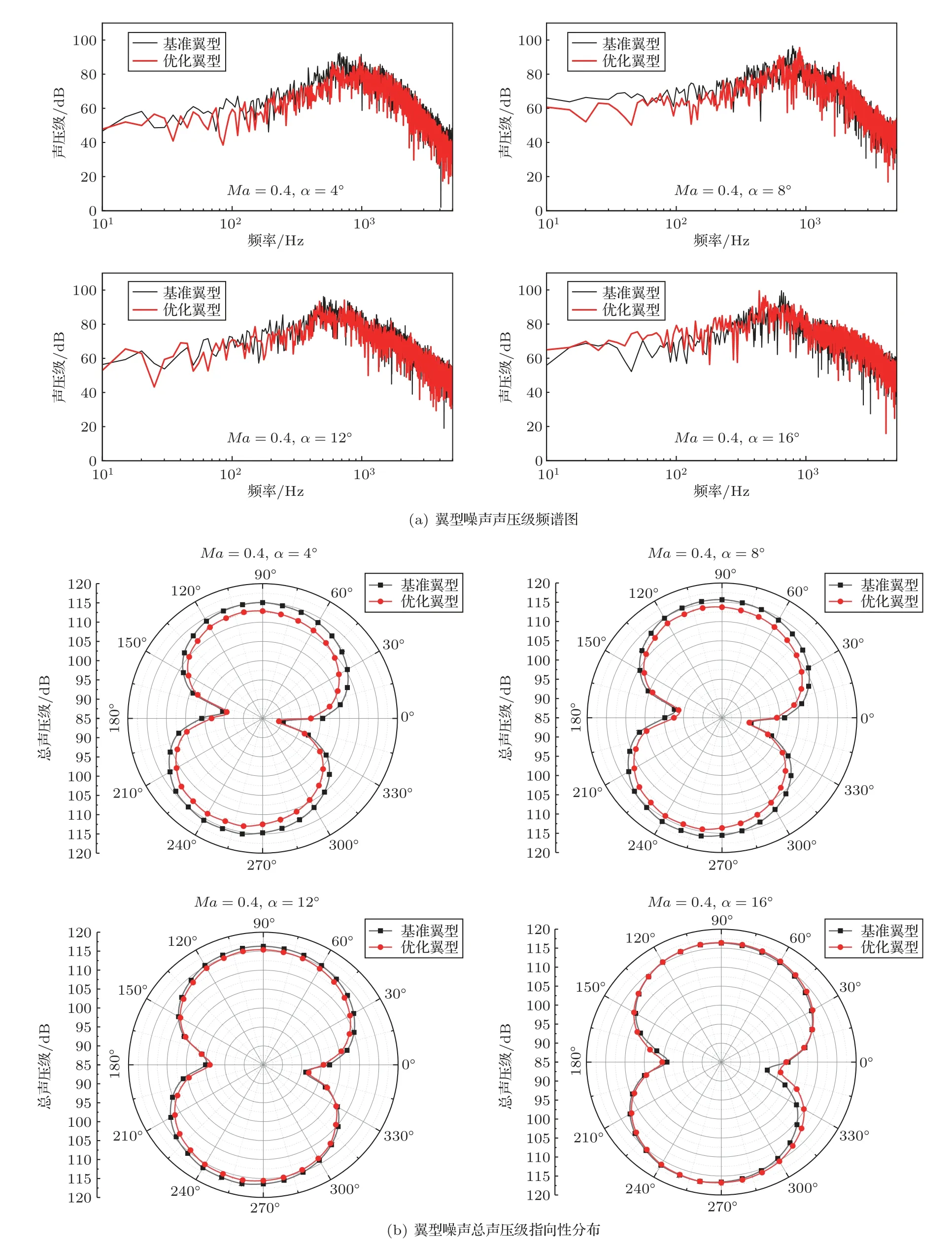
式(9)中:e(k)=lg 0.5/lgxk,0 本文的研究對象RAF-6 翼型為非對稱的平底翼型,為避免過多地改變翼型的氣動特性,將不對翼型的下表面進行修改,僅在翼型上表面取5 個xk(k=1,2,3,4,5),這5 個點分別位于翼型弦長的16%、36%、52%、68%及84%處,對應的型函數如圖5所示。 圖5 型函數圖像Fig.5 Shape function 本文使用遺傳算法作為翼型噪聲的優化方法,若以常規的遺傳算法進行計算,為評估每個樣本的適應度,需要對每一個樣本進行仿真計算,而遺傳算法所需的樣本數量往往是非常龐大的,這就使得優化過程的計算量過大且耗時過長,所以本文將引入響應面模型,通過對部分樣本進行計算,從而擬合出優化所需的適應度函數,進而進行優化計算。 響應面模型(Response surface methodology,RSM)的構建過程是根據試驗設計的原理,在一定設計空間內選取一定數量的樣本,通過樣本的試驗結果擬合出多項式。通過合理地選擇設計空間與樣本,響應面擬合出的多項式可以準確地預測未經試驗的樣本的響應值,這種方法可以大大提高工作效率,節省試驗或計算的時間,如今已得到廣泛的應用。 本文采用完全二階多項式擬合,該多項式形式如下: 式(10)中:f(x)為響應值;C0、Ci、Cii、Cij為回歸系數;x即為設計變量。 在本文中x即為型函數的系數ck(k=1,2,3,4,5),變量的取值區間為[-0.03,0.03]。隨著ck取值的不同,翼型的最大厚度與彎度也隨之變化,最大厚度的變化范圍為[0.0428c,0.174c],而對于RAF-6翼型最大彎度值為最大厚度值的1/2。 遺傳算法是一種較為常用的優化算法,尤其在翼型的氣動優化問題上已得到成熟的運用,由Holland[18]提出,它借鑒生物界的自然選擇法則與生物遺傳的機制,是一種隨機的優化模型。遺傳算法的優勢在于可以快速地在龐大且復雜的搜索空間中找到最優解,可避免搜索陷入局部最優的情況。 遺傳算法的一般流程模擬了自然界生物種群繁衍、基因遺傳與交叉的過程,首先獲得一個具有一定個體數量的初始種群,之后對種群中的個體進行選擇、交叉、變異等操作產生子代個體和種群,通過比較子代的適應度進而產生新的父代種群,在經過對以上步驟的循環迭代,直至產生符合要求的最優個體。 由于翼型的CFD計算與噪聲計算耗時久,故遺傳算法所需的適應度函數由構建響應面獲得,本文的優化流程如圖6所示。 圖6 優化流程Fig.6 Flow chart of optimization 使用上文所述的優化方法對某型電動水上飛機螺旋槳所使用的RAF-6 翼型進行優化設計,取槳葉長度75%處翼型計算。翼型弦長0.114 m,來流馬赫數Ma為0.4,基于弦長的雷諾數Re為1×106,來流攻角α=8?。 首先構建響應面模型,使用1.2 節所述計算方法,共對45 個翼型樣本進行了計算,使用完全二次多項式擬合得到了預測翼型聲壓級(接收點28 處)、升力系數CL及阻力系數CD的多項式。 使用遺傳算法進行優化,本文優化設計旨在使翼型獲得設計狀態下較好的聲學與氣動性能,同時翼型的升阻比不會過多的衰減,故以氣動噪聲與升阻比的加權運算作為優化的目標函數,以型函數的系數作為設計變量,以翼型的升、阻力系數變化不超過10%為約束所構建的優化模型如式(11)所示: 式(11)中:f(x)為適應度函數;α、β為翼型聲壓級與升阻比的加權系數(α+β=1),取0.5;CL0、CD0為基準翼型的升、阻力系數。 本文所使用遺傳算法中,初代種群規模為200,最大迭代次數為2000。經過遺傳算法優化得到了翼型的優化結果,基準翼型與優化翼型的形狀對比如圖7 所示。由圖可見,相較于基準翼型,優化翼型的前緣厚度明顯減小,翼型的最大厚度位置后移,優化翼型中段的厚度也有所減小,而在翼型后端優化翼型的厚度略大于基準翼型。 圖7 優化翼型與基準翼型Fig.7 Optimized airfoil and original airfoil 使用1.2節所述計算方法對優化翼型進行計算,計算結果與響應面預測結果對比如表2所示。 表2 響應面預測值與計算值對比Table 2 Comparison of RSM result and simulation result 由表3知,在設計狀態下,優化翼型相較于基準翼型,聲壓級降低了2.17 dB,升阻比提高了1.12%,升、阻力系數的變化滿足約束條件,未超過10%,可見本次優化達到了優化目標。 表3 基準翼型與優化翼型對比Table 3 Comparison of original airfoil and optimized airfoil 圖8 為設計狀態基準翼型與優化翼型表面壓力系數分布對比圖。由于并未對翼型下表面進行修改,所以翼型下表面,即壓力面的壓力系數分布無明顯變化。在翼型的上表面,翼型前緣半徑的降低令優化翼型前緣產生了較高的負壓,但負壓的快速下降導致了優化翼型升力系數較基準翼型有所減小,而優化翼型中段較為“平緩”且后段的厚度增加,使得翼型吸力面中段負壓高于基準翼型。 圖8 翼型壓力系數分布Fig.8 Pressure coefficient distributions of airfoils 圖9 與圖10 分別為優化翼型氣動與聲學性能隨攻角變化圖,并且與基準翼型進行了比較。由圖9(a)可見,基準翼型的失速攻角為13?,而優化翼型的失速攻角提前了1?位于12?左右,可見優化翼型在厚度上的改變對翼型的失速特性產生了一定的影響。當攻角小于10?,優化翼型升力系數相較于基準翼型有所減小,但變化趨勢較為一致,并且阻力系數低于基準翼型;而當攻角大于10?,優化翼型的升力系數衰減較大,且阻力系數大于基準翼型。圖9(b)為優化前后翼型升阻比對比,橫坐標為翼型升力系數。由圖9(b)可知當升力系數小于1.2,優化翼型升阻比大于基準翼型,但在最大升力系數處,優化翼型升阻比小于基準翼型。由此可見,本文的優化設計結果雖改變了翼型的失速攻角,但卻使翼型在包括設計狀態的小攻角狀態下的氣動性能有所提升。 圖9 翼型氣動性能對比Fig.9 Comparison of aerodynamic performance of airfoils 圖10 翼型聲學性能對比Fig.10 Comparison of acoustic performance of airfoils 圖10(a)為翼型噪聲聲壓級頻譜圖,頻率范圍為0~5000 Hz,可以看出在4?、8?攻角下,低頻段優化翼型的降噪效果比較明顯,而低頻段的降噪效果隨攻角的增加逐漸減弱,在16?攻角時降噪效果不明顯。圖10(b)為翼型噪聲總聲壓級指向性分布圖,可見優化并未改變翼型噪聲的指向性,降噪效果隨攻角的變化則與圖10(a)一致。綜上可知,本文優化設計對小攻角狀態的翼型具有較好的降噪效果,而對大攻角狀態的翼型降噪效果一般。 (1) CFD/FW-H 方法可以準確地計算翼型升、阻力系數與氣動噪聲,計算值與試驗值誤差較小。 (2) 在遺傳算法中使用響應面擬合多項式代替適應度函數,可以減少調用仿真計算的次數,顯著地提高了優化模型的效率。并且響應面預測值與計算值的誤差小,預測精度高。 (3) 提出以翼型噪聲與氣動性能為目標的翼型優化設計,使翼型在設計狀態下的氣動噪聲得到了顯著的降低并且翼型的氣動性能得到了保證。而且優化翼型在小攻角狀態下的氣動與聲學性能均得到了明顯改善。說明本文所使用優化方法行之有效,具有一定的應用價值,可推廣應用至其他螺旋槳翼型優化設計。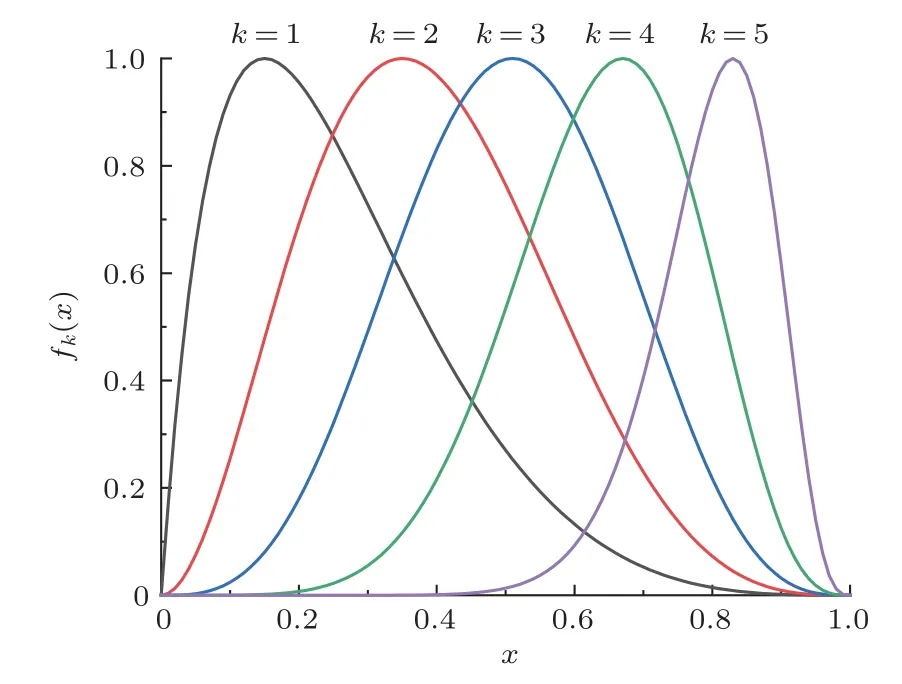
3 優化方法
3.1 響應面模型
3.2 遺傳算法
4 翼型優化設計
5 結論

