混雜纖維超高性能混凝土力學性能尺寸效應

王 龍， 池 寅， 徐禮華， 劉素梅， 尹從儒

（1.武漢大學土木建筑工程學院，湖北武漢 430072；2.中國人民解放軍陸軍勤務學院，重慶 401331）

混雜纖維超高性能混凝土（HF-UHPC）是一種 新型高性能水泥基復合材料，其力學性能不僅與材料 組 分 有 關［1］，還 與 材 料 尺 寸 息 息 相 關［2］.對HF-UHPC 開展力學性能尺寸效應研究，揭示不同尺寸下HF-UHPC 的力學性能響應規律，對UHPC 強度預測及工程結構設計具有重要應用價值.

目前，學者們針對超高性能混凝土（UHPC）力學性能的尺寸效應進行了研究.如陳寶春等［3］和羅晨熙［4］開展了含鋼纖維UHPC 抗壓強度的尺寸效應研究，得到不同尺寸試件立方體抗壓強度的換算關系.Fládr 等［5］發現粗骨料高強纖維混凝土抗壓強度隨著試件尺寸的增大而減小，且隨著抗壓強度的提高，尺寸效應逐漸減弱.Kazemi等［6］得到類似的抗壓強度尺寸效應規律.蘇捷等［7］研究了不同強度等級和鋼纖維摻量對UHPC 立方體抗壓強度尺寸效應的影響，得到立方體抗壓強度尺寸效應規律，并建立了尺寸效應律參數的計算公式.

上述研究成果主要考慮了混凝土強度等級及鋼纖維參數（摻量和長徑比）對UHPC 抗壓強度尺寸效應的影響，并未考慮鋼-聚丙烯混雜纖維的共同作用，且對于HF-UHPC 單軸受壓下的應力-應變曲線、峰值強度、峰值應變和彈性模量等力學性能尺寸效應的研究相對缺乏.因此，本文通過改變纖維參數（鋼纖維摻量（體積分數）、鋼纖維長徑比和聚丙烯纖維摻量（體積分數）），考察了HF-UHPC 力學性能尺寸效應的變化規律，并揭示了HF-UHPC 抗壓強度尺寸效應機理；同時在無切口修正的Ba?ant 斷裂力學尺寸效應理論基礎上，建立了可應用于不同纖維參數的HF-UHPC 抗壓強度尺寸效應律參數計算公式，為UHPC 強度預測及工程設計提供參考.

1 試驗

1.1 原材料及基準配合比

水泥為P·O 52.5 普通硅酸鹽水泥；石英砂，粒徑為0.4～0.6 mm；硅灰，活性指數130%；S95 級礦渣粉，活性指數105%；減水劑為聚羧酸減水劑，減水率大于35%（質量分數）；拌和水為自來水.此外，2種纖維分別為：鍍銅平直型鋼纖維（SF），直徑為0.200 mm，抗拉強度大于2 500 MPa，鋼纖維長徑比（lsf/dsf）為30、60、80；聚丙烯纖維（PF），直徑為0.048 mm，抗拉強度大于358 MPa，聚丙烯纖維長徑比（lpf/dpf）為167.結合課題組前期研究成果［8］，確定HF-UHPC 基準配合比，見表1.

表1 UHPC 基準配合比Table 1 Base mix proportion of UHPC kg/m3

1.2 試驗參數設計

以鋼纖維摻量、鋼纖維長徑比和聚丙烯纖維摻量為變化因素，聚丙烯纖維長徑比固定為167，設計8 種配合比HF-UHPC 試件，其纖維參數如表2所示.分別制作邊長為70.7 mm（A 組）、100 mm（B 組）、150 mm（C組）、200 mm（D組）的4種立方體試件和70.7 mm×70.7 mm ×212.1 mm（E 組）、100 mm ×100 mm ×300 mm（F 組）、150 mm ×150 mm×450 mm（G組）、200 mm×200 mm×600 mm（H組）的4種棱柱體試件.除B、F 試件各制作2 組外，其他尺寸試件各制作1 組，每組3塊試件，共計240塊試件.

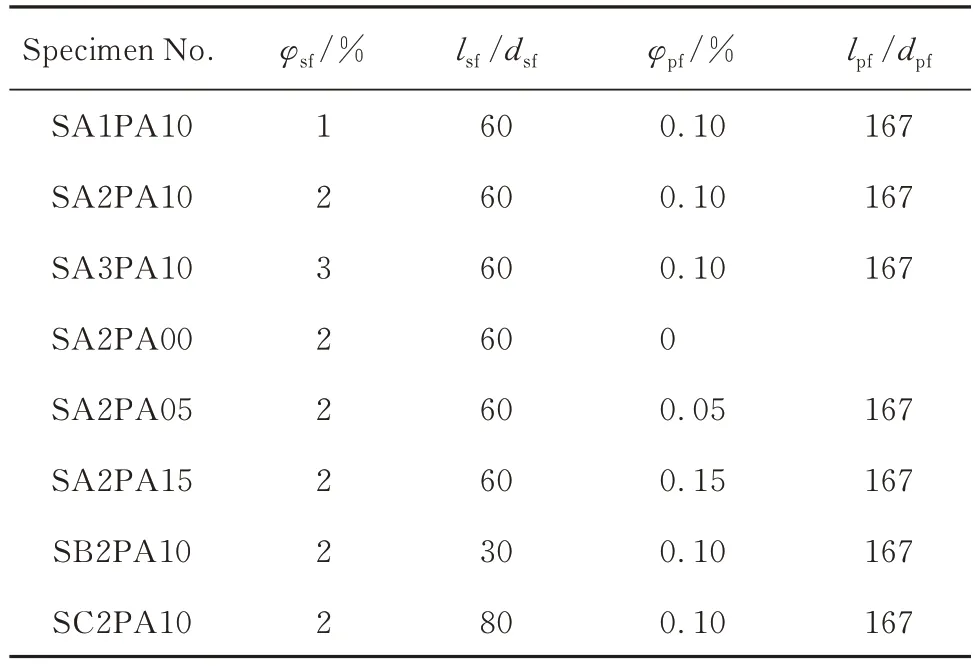
表2 HF-UHPC 試件的纖維參數Table 2 Fiber parameter of HF-UHPC specimens

1.3 試件制備及加載

試件制備步驟如下：（1）依次稱取各組分材料；（2）將水泥、礦渣粉、硅灰及石英砂加入攪拌機，攪拌5 min；（3）將水、減水劑及聚丙烯纖維混合均勻，分2 次加入攪拌機，攪拌5 min；（4）均勻撒入鋼纖維，攪拌5 min，以保證混合均勻；（5）攪拌結束后，將混凝土倒入模具中振搗1 min，模具表面覆蓋保鮮膜；（6）常溫養護24 h 脫模，放入45 ℃的養護室內蒸汽養護28 d.

依據GB/T 31387—2015《活性粉末混凝土》進行試驗加載，其中A、B、E、F 組試件采用2 500 kN 的MTS 壓力試驗機，其余組別試件采用30 000 kN 電液伺服壓力試驗機.立方體抗壓強度試驗采用荷載控制，加載速率為1.2 MPa/s；軸壓力學性能試驗采用位移控制，加載速率為0.002 mm/s，通過位移計和壓力傳感器測量試件的載荷-位移曲線.

2 試驗結果及分析

2.1 立方體抗壓強度尺寸效應分析

圖1 展示了HF-UHPC 試件的立方體抗壓強度平均值，立方體抗壓強度變異系數小于4.05%，表明試驗數據離散程度較低.由圖1 可知，相同配合比HF-UHPC 的立方體抗壓強度存在顯著的尺寸效應，并隨著試件尺寸的增大而逐漸降低.例如，當HF-UHPC 配合比為SA2PA10 時，邊長為100、150、200 mm 立方體試件的抗壓強度較邊長為70.7 mm 試件分別下降了5.46%、11.69%、16.49%.

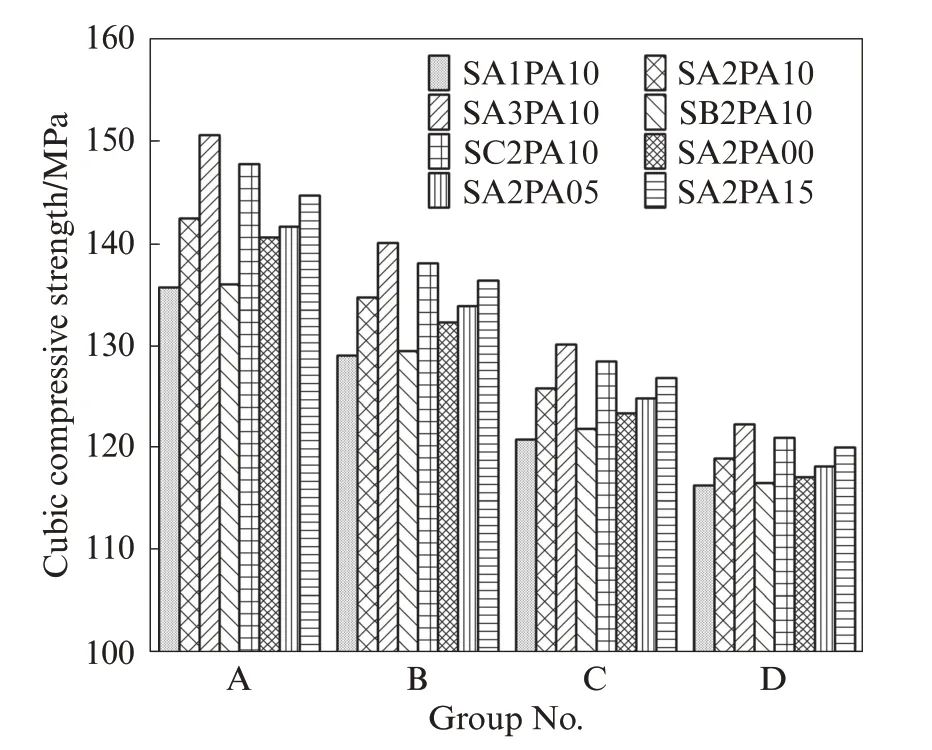
圖1 HF-UHPC 試件的立方體抗壓強度Fig.1 Cube compressive strength of HF-UHPC specimens

2.2 單軸受壓力學性能尺寸效應分析

2.2.1 應力-應變全曲線尺寸效應

通過對不同尺寸、不同纖維參數的HF-UHPC棱柱體試件進行軸壓力學性能試驗，發現其應力-應變（σ-ε）曲線變化過程基本相同，均包含彈性階段、裂縫穩定發展階段、裂縫失穩擴展階段和破壞階段.以配合比為SC2PA10 的不同尺寸棱柱體試件為例進行分析，其應力-應變曲線如圖2 所示.結合文獻［9］對試件受壓全過程力學性能尺寸效應進行分析：

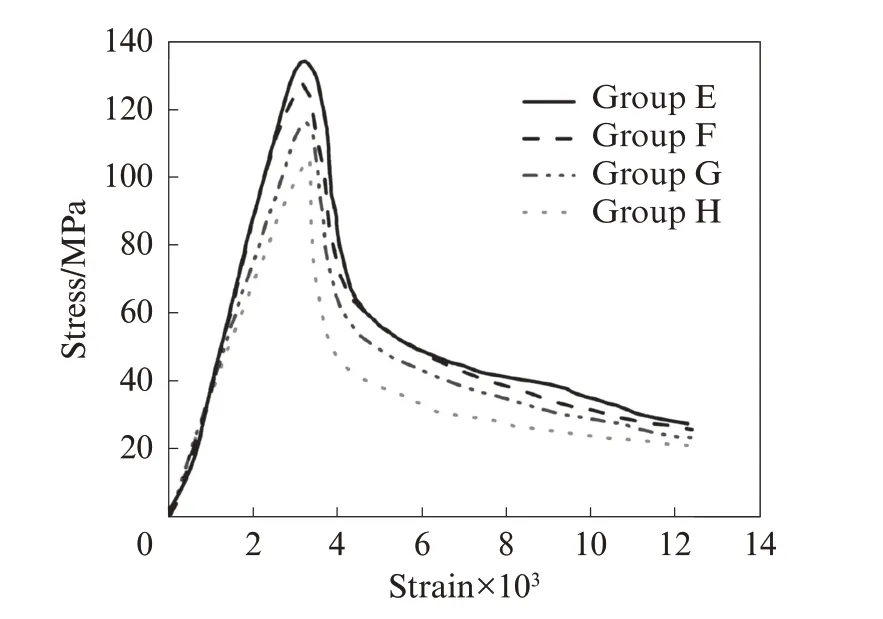
圖2 HF-UHPC 棱柱體試件的應力-應變曲線Fig.2 Stress-strain curves of HF-UHPC prism specimens

（1）彈性階段（σ≤70%fc（峰值強度）） 該階段，各HF-UHPC 試件的應力-應變關系均呈線性增長趨勢，且應力-應變關系曲線斜率（即彈性模量）基本相同，與試件尺寸無關.該階段混凝土的變形主要為試件本身受壓后的彈性變形，未產生微裂紋和裂縫.

（2）裂縫穩定發展階段（70%fc＜σ≤fc） 該階段，各HF-UHPC 試件的應力-應變全曲線呈現較為明顯的非線性特征，尺寸效應逐漸顯現.具體表現為：小尺寸HF-UHPC 試件的切線剛度高于大尺寸試件，且隨著試件尺寸的增大，切線剛度的差異性逐漸增加；HF-UHPC 試件的峰值強度隨著試件尺寸的增大呈現規律性降低，峰值應變隨著試件尺寸增大呈現規律性升高.

（3）裂縫失穩擴展階段（fc＞σ≥40%fc） 該階段，各HF-UHPC 試件的應力-應變曲線向下彎曲，試件出現貫通裂縫，裂縫間的聚丙烯纖維逐漸被拉斷，鋼纖維逐漸被拔出；此階段受壓試件尺寸越大，峰后應力-應變曲線下降越快，原因在于裂縫擴展速率與試件尺寸有關，且在很大程度上隨著試件結構尺寸的平方而增加［11］，從而導致應力-應變曲線下降段更加陡峭.

（4）破壞階段（40%fc＞σ） 該階段，試件的貫通裂縫在剪應力作用下不斷發展加寬，鋼纖維繼續被拔出，聚丙烯纖維繼續被拔斷，試件整體失去結構意義.從HF-UHPC 試件的應力-應變曲線所圍面積可以看出，HF-UHPC 試件尺寸越小，韌性越大，試件破壞吸收的能量值就越高.

2.2.2 關鍵力學性能指標尺寸效應

圖3展示了不同尺寸HF-UHPC 棱柱體試件的關鍵力學性能指標平均值，其中峰值強度、峰值應變和彈性模量的變異系數分別小于4.75%、7.43%、5.30%，表明試驗結果離散性較小.由圖3可知：HF-UHPC 棱柱體試件的峰值強度和峰值應變存在尺寸效應，且隨著試件尺寸的增大，峰值強度逐漸降低，峰值應變逐漸增大，彈性模量尺寸效應不明顯，可以忽略.例如，HF-UHPC 配合比為SA2PA10時，尺寸為100 mm×100 mm ×300 mm、150 mm ×150 mm ×450 mm、200 mm×200 mm×600 mm 的棱柱體峰值強度較尺寸為70.7 mm ×70.7 mm ×212.1 mm 的棱柱體分別下降6.29%、13.15%、17.70%；峰值應變分別升高3.40%、5.82%、7.61%；彈性模量變化幅度較小，分別升高1.23%、下降1.18%、升高0.99%.

圖3 HF-UHPC 棱柱體試件的關鍵力學性能指標Fig.3 Key mechanical performance indexes of HF-UHPC prism specimens

3 尺寸效應規律分析

3.1 纖維參數對尺寸效應的影響

引入尺寸效應度［7］對HF-UHPC 的力學性能尺寸效應進行定量分析.以邊長70.7 mm 的立方體試件和70.7 mm×70.7 mm×212.1mm 的棱柱體試件為基準試件，其余尺寸試件為非基準尺寸試件進行分析.HF-UHPC 試件的立方體抗壓強度尺寸效應度（Δαx）、峰值強度尺寸效應度（Δβx）和峰值應變尺寸效應度（Δrx）計算公式如式（1）～（3）所示.

式中：fcu，70.7、fcu，x分別為邊長為70.7 mm 和xmm 試件的立方體抗壓強度，MPa；fc，70.7、fc，x分別為70.7 mm×70.7 mm×212.1 mm 和xmm×xmm×3xmm 棱柱體試件的峰值強度，MPa；ε70.7、εx分別為70.7 mm×70.7 mm×212.1 mm 和xmm×xmm×3xmm 棱柱體試件的峰值應變；x表示試件的長度，分別取為100、150、200 mm.

圖4 為HF-UHPC 試件的力學性能尺寸效應度.由圖4 可知：隨著鋼纖維摻量或鋼纖維長徑比的增大，HF-UHPC 的立方體抗壓強度、峰值強度和峰值應變尺寸效應度呈現增大趨勢；隨著聚丙烯纖維摻量的增大，HF-UHPC 的立方體抗壓強度、峰值強度和峰值應變尺寸效應度先減后增，變化幅度較小.例如，相比鋼纖維摻量為1%的HF-UHPC，鋼纖維摻量為2%、3% 的HF-UHPC 力學性能尺寸效應度Δα100增 加11.20%、42.86%，Δβ100增 加21.45%、35.91%，Δγ100增加23.99%、30.21%；相比鋼纖維長徑比為30 的HF-UHPC，鋼纖維長徑比為60、80 的HF-UHPC 的Δα100增加14.13%、37.22%，Δβ100增加13.83%、22.92%，Δγ100增加8.32%、30.84%；相比聚丙烯纖維摻量為0%的HF-UHPC 試件，聚丙烯纖維摻 量 為0.05%、0.10%、0.15%HF-UHPC 試 件 的Δα100減小6.57%、7.45%、2.65%；Δβ100減小3.56%、4.30%，增加1.82%；Δγ100減小6.40%、8.22%，增加2.54%.

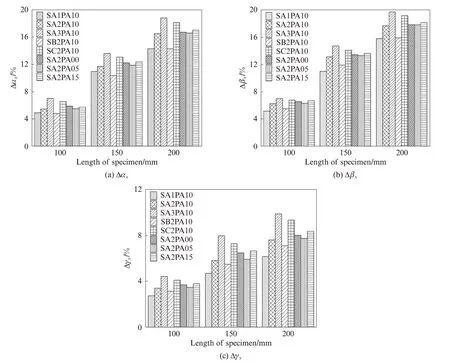
圖4 HF-UHPC 試件的力學性能尺寸效應度Fig.4 Size effect parameter for mechanical property of HF-UHPC specimens

3.2 抗壓強度尺寸效應機理

裂縫產生過程中能量釋放率和能量吸收率間的不匹配是混凝土存在尺寸效應的根源，且能量釋放率很大一部分隨著試件尺寸平方的增加而增大，能量 吸 收 率 則 隨 試 件 尺 寸 線 性 增 大［10］.圖5 為HF-UHPC 抗壓強度尺寸效應產生機理示意圖.由圖5（a）可見：當試件處于臨界失穩階段時，能量釋放率等于能量吸收率［11］；相比小尺寸試件，大尺寸試件能量吸收率雖有所增大，但其能量釋放率增速更加顯著，致使大尺寸試件的相對裂縫深度（a/D）小于小尺寸試件，從而導致失穩破壞提前，產生抗壓強度尺寸效應.由圖5（b）可見：鋼纖維在裂縫區起到橋接作用，能夠有效抑制裂縫的展開，并不斷消耗能量；由于小尺寸試件相對裂縫深度更大，裂縫間“有效”作用的鋼纖維更多，纖維的增強作用更加明顯，導致HF-UHPC 抗壓強度尺寸效應愈發顯著；隨著鋼纖維摻量或鋼纖維長徑比的增大，不同尺寸試件的纖維增強作用差異增大，裂縫寬度比增加，導致HF-UHPC 抗壓強度尺寸效應更加顯著.由圖5（c）可見：聚丙烯纖維主要作用于斷裂過程區，可有效抑制微裂紋的擴展并消耗能量，但由于臨界失穩階段斷裂過程區長度與試件尺寸的比值為定值［12］，導致體積分數相同的聚丙烯纖維對幾何外形相似的試件增強效果相同；另外，聚丙烯纖維為低彈性模量材料，對試件的抗壓強度影響較弱.因此，隨著聚丙烯纖維摻量的增加，HF-UHPC 抗壓強度尺寸效應度相對略微下降；當聚丙烯纖維摻量過多時，混凝土內部易形成薄弱點，削弱試件的力學性能，反而會加劇HF-UHPC 抗壓強度尺寸效應.

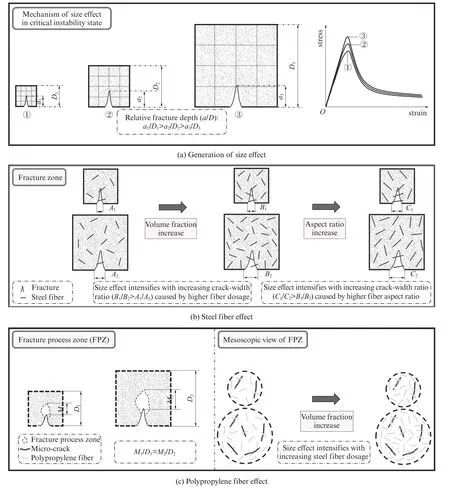
圖5 HF-UHPC 抗壓強度尺寸效應產生機理Fig.5 Mechanism of size effect on compressive strength of HF-UHPC

3.3 尺寸效應律

Ba?ant［10］引入無窮大名義強度（f∞r）和邊界層開裂有效厚度（Db）這2 個參數，得到材料失效時的名義強度尺寸效應律，即無切口修正的Ba?ant 尺寸效應律公式：

式中：σN為受壓破壞時的名義強度；D為立方體邊長或棱柱體高度.

將試驗得到的HF-UHPC 立方體抗壓強度及棱柱體峰值強度實測值σN代入式（4）中進行擬合分析，得到不同配合比下HF-UHPC 抗壓強度尺寸效應律公式的參數值f∞r和Db.HF-UHPC 試件的尺寸效應擬合參數及相關系數見表3.基于表3 數據，建立HF-UHPC 尺寸效應律公式參數與抗壓強度及鋼纖維和聚丙烯特征參數（λsf、λpf）的關系，其關系式見式（5）～（8）.

表3 HF-UHPC 試件的尺寸效應擬合參數及相關系數Table 3 Size effect simulation parameter and correlation coefficient of HF-UHPC specimens

式中：fcu，100、fc，100分 別為標 準試件 的立方 體抗壓強度和軸心抗壓強度；λsf=φsf×lsf/dsf；λpf=φpf×lpf/dpf.

通過上述關系式可以定量分析纖維參數對HF-UHPC 抗壓強度尺寸效應的影響程度，即不同纖維參數下HF-UHPC 抗壓強度隨尺寸變化的規律.利用式（5）～（8）對文獻［3-4，7］進行HF-UHPC 抗壓強度尺寸效應分析，將其立方體抗壓強度預測值與試驗值進行對比，如圖6 所示.圖6 顯示精確度大于91.5%，表明式（5）～（8）預測精確度較高.

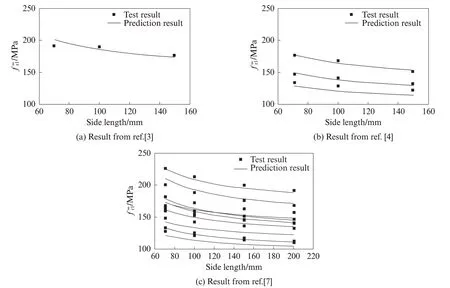
圖6 HF-UHPC 抗壓強度預測結果和實際結果對比Fig.6 Comparison between compressive strength predicted results and actual results of HF-UHPC

4 結論

（1）HF-UHPC 立方體抗壓強度和軸心抗壓強度均存在顯著的尺寸效應.該尺寸效應隨著鋼纖維摻量或鋼纖維長徑比的增大而增大；隨著聚丙烯纖維摻量的增大呈現先減后增趨勢，且變化幅度較小.

（2）HF-UHPC 軸心受壓峰值應變存在顯著的尺寸效應.該尺寸效應隨著鋼纖維摻量或鋼纖維長徑比的增大呈現增大趨勢；隨著聚丙烯纖維摻量的增大呈現先減后增趨勢，且變化幅度較小.HF-UHPC彈性模量尺寸效應可以忽略不計.

（3）基于無切口修正的Ba?ant 斷裂力學尺寸效應理論，建立了尺寸效應律參數f∞r和Db的計算公式，可用于不同尺寸、不同纖維參數HF-UHPC 抗壓強度的計算.