具有非慣量負載轉矩補償功能的伺服永磁同步電機控制方法*
毛 帥, 刁曉飛, 王 曉, 王先強, 周 輝
(1.山東理工大學 電氣與電子工程學院,山東 淄博 255000;2.中國計量科學研究院 幾何量計量科學研究所,北京 100029;3.中電裝備山東電子有限公司, 山東 濟南 250101)
0 引 言
永磁同步電機(PMSM)伺服系統的負載一般為轉動慣量值固定的慣性負載,對于較為精密的永磁伺服運動系統來說,一般不會有外界擾動,不用考慮外界擾動造成的負載轉矩[1-2],比如激光跟蹤儀的伺服運動旋轉系統。因為負載的重心不是準確地位于旋轉軸線上,所以在不同旋轉位置上重力會引起不同的負載轉矩,如圖1所示。

圖1 負載重力轉矩示意圖
圖1所示的電機負載在伺服控制中慣量不變,其重力引起的負載轉矩隨旋轉位置不斷變化而變化,因此要精確控制該負載旋轉運動,需要實現抗擾動控制。目前學者們主要研究了抗階躍突變式轉矩擾動的控制方法[3-4],研究思路是在控制系統中加入擾動觀測器,觀測出擾動量,從而對其進行補償[5-8]。當然擾動觀測器也可以觀測出時變的擾動轉矩[9-10],但是觀測時一般不考慮黏性阻尼并且由于擾動觀測器有觀測收斂過程,在電機處于穩定運行狀態自轉速恒定時觀測出的擾動轉矩才準確,如果轉速不斷變化(例如處于伺服運動中),則會造成所觀測出的擾動與實際值存在偏差,當該觀測擾動加入控制對其補償抑制時,可能會導致擾動補償抑制的過沖和不足。針對圖1的伺服控制過程,本文在考慮黏性阻尼系數和實時擾動補償準確性的前提下,設計了一種基于負載辨識的永磁同步電機負載轉矩補償的控制方法。
1 負載轉矩辨識
理想伺服旋轉系統中,負載質心位于轉軸軸線上,因此旋轉運動中不用考慮重力引起的負載轉矩,但實際上負載質心不可能準確位于轉軸上,其與轉軸必然會存在一個力臂距離,負載質心與轉軸對應的運動學關系如圖2所示。
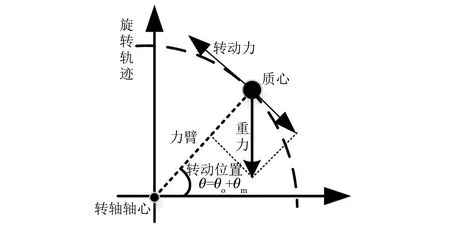
圖2 負載質心不位于轉軸上對應的運動學關系
伺服電機的運動學方程式為

(1)
式(1)中的負載轉矩TL需要按照圖2所示替換為不同旋轉位置上重力引起的負載轉矩,因此可得圖2所示的伺服電機運動學方程式為

(2)
式中:Te為電機輸出轉矩;J為轉動慣量;Bm為黏性阻尼系數;ωm為電機的機械角速度;F為負載的重力力矩;θo為負載初始旋轉時的位置角度;θm為電機的機械旋轉角位移。
若為表貼式永磁同步電機,并滿足最大轉矩電流比控制時,電機輸出轉矩表示為
Te=Kt×Iq
(3)
式中:Kt為電機轉動常數;Iq為電機的q軸電流。
式(2)中,J、Bm、F和θo為需要辨識的參數,其他參數為已知或可測量。為便于使用擬合方法,將式(2)改寫為
Fsinθosinθm=KtIq
(4)
建立如式(4)所示的擬合模型函數式,J、Bm、Fcosθo和Fsinθo為需要辨識的參數。Fcosθo和Fsinθo這兩個參數進行平方和運算然后開根號便可得參數F,進行比例運算求反正切角便可得參數θo。給予永磁電機伺服電機系統一組單調遞增或遞減線性速度命令,便可得到Iq、ωm和θm各自對應的一組測量數據。最后,便可以通過基于模型函數式(4)的非線性回歸擬合方法得到四個需要辨識的參數。
這里所用的非線性擬合方法為(Levenberg-Marquardt)方法[11]。其偽代碼如下:
Begin
k=0;v=2;θ=θo
H=JTJ;g=JTr

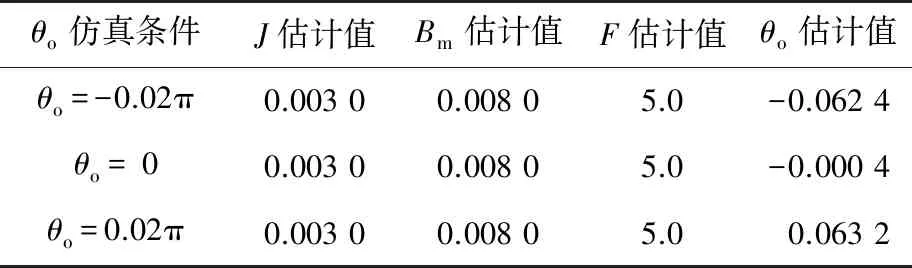
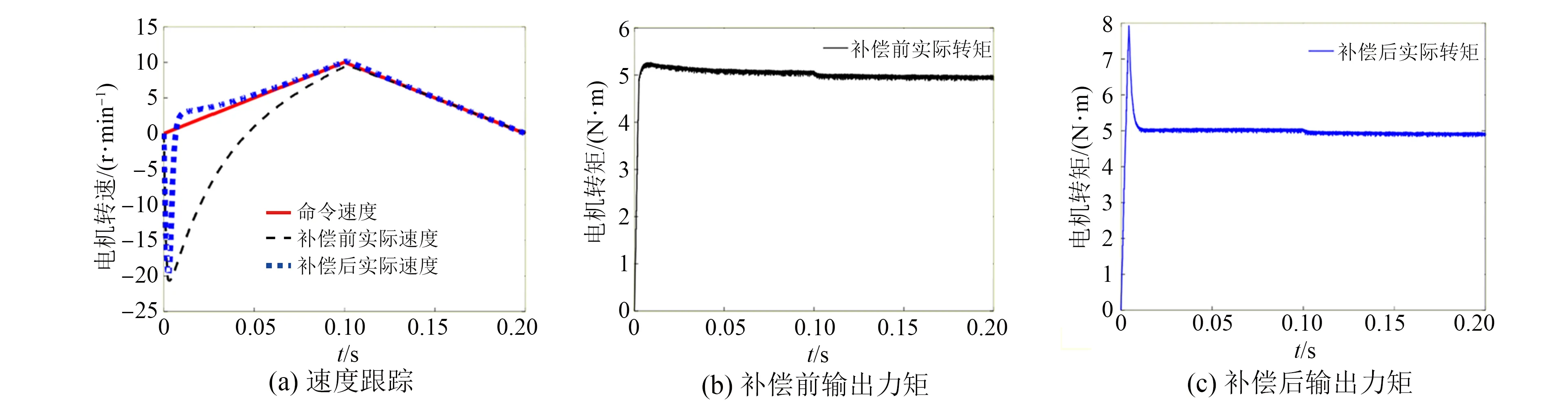
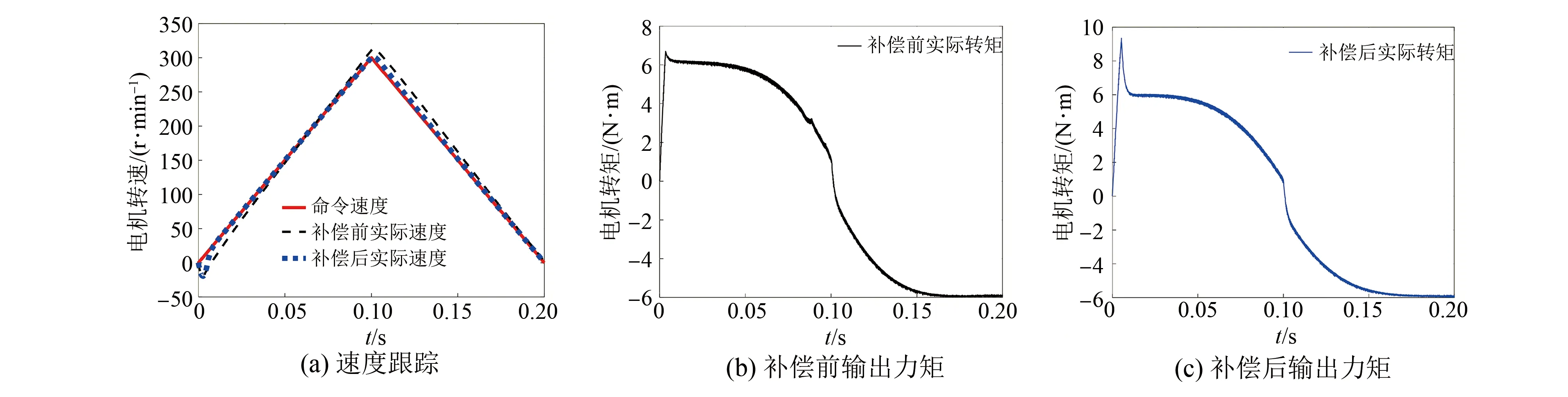
while (notfound) and (k k=k+1; found:=true else θnew=θ+λ ρ=2(F(θ)-F(θnew))/λT(μλ-g) ifρ>0 θ=θnew;H=JTJ;g=JTr v=2 else μ=μ*v;v=2*v End 其中:k為迭代計算次數;τ,1和2分別為微小常量值;hjj為矩陣H的對角元素值;θo是θ的初始估計值。 假設測量的數據組數為m,其組號i≤m,需要辨識的參數為四個,所以參數編號j≤4。每次測量后得到一個向量和一個標量,其表達式為 (5) yi=(KtIq)i (6) θ為需要辨識參數的估計向量,其表達為 (7) 每次測量數據對應的殘差ri的表達式為 ri=yi-θTxi (8) 式中:x為殘差向量r,r=[r1r2r3…ri…rm]T。 Jacobian矩陣J為m行4列的矩陣,其中每行數據是以θ為自變量的函數行向量表達式: (9) 另外,偽代碼中F(θ)可表示為 (10) 經典電機控制即主要通過PI調節的電流環和速度環實現電機的控制[12-13],如圖3所示。其中,電流環可以等效為一個一階慣性環節1/(1+Tis)(Ti為電流環帶寬倒數),該等效的前提是不考慮非慣量的負載轉矩,并且要求d軸和q軸的電壓值是電流完全解耦后的電壓值。 圖3 電流環和速度環結構框圖 電流環d軸和q軸的電流完全解耦可以采用前饋解耦控制策略來實現。不考慮非慣量的負載轉矩表達式為 (11) 在實際工程中不能不考慮非慣量的負載轉矩對控制的影響,此時需從機械運動學角度來考慮,則需要滿足等式: (12) (13) (14) 整體模型圖如圖3中虛線框模塊所示。 整體的控制模型(Simulink模型)如圖4所示。其中的(Load torque caused by gravity)和(Load torque estimation)模塊輸出分別為Fcos(θo+θm)仿真結果和參數辨識后得到的估計值,Load compensation模塊輸出為參數辨識后的[Bmωm+Fcos(θo+θm)] ×(1+Tis)/Kt。圖4中的參數flux、L和Pn分別為磁鏈、定子電感和極對數,電流環采用前饋解耦控制策略。參數辨識階段,Load compensation模塊輸出不用加入到電流環的前端,只使用經典的PI電機控制;負載補償階段,Load compensation模塊輸出加入到電流環的前端。仿真參數設置取值:極對數為4,定子電感為12 mH,定子電阻為0.958 Ω,磁鏈為0.182 7 Wb (可得電機轉動常數Kt=1.096 2),轉動慣量J為0.003 kg·m2,阻尼系數Bm為0.008 N·m·s,負載的重力力矩F分別設置為0.2 N·m和5 N·m,電機母線電壓為81 V。 圖4 具有負載重力轉矩補償功能的整體模型圖 仿真θo分別為±0.02π rad和0 rad三種條件下對應的參數辨識結果。給予圖4系統的速度命令函數為100 t,通過非線性回歸擬合方法辨識重力力矩0.2 N·m和5 N·m條件下的參數,參數辨識對應的速度和輸出轉矩情況如圖5和圖6所示,結果如表1和表2所示。 表1 重力力矩0.2 N·m參數辨識結果 表2 重力力矩5 N·m參數辨識結果 圖5 力矩為0.2 N·m條件下辨識對應的速度和力矩 圖6 力矩為5 N·m條件下辨識對應的速度和力矩 由表1和表2可知,通過回歸擬合可以比較準確地辨識出相應參數,除了θo外其他參數都為其仿真值。圖7~圖14是在三角波和正弦速度函數命令輸入情況下負載補償前和補償后對應的速度跟蹤情況和輸出力矩結果(注:三種不同θo值輸出情況一致,所以未特意說明結果所對應的θo值)。 圖7 力矩為0.2 N·m條件下三角波低速度函數命令輸入時速度跟蹤情況和輸出力矩結果 圖8 力矩為5 N·m條件下三角波低速度函數命令輸入時速度跟蹤情況和輸出力矩結果 圖10 力矩為5 N·m條件下三角波高速度函數命令輸入時速度跟蹤情況和輸出力矩結果 圖11 力矩為0.2 N·m條件下正弦低速度函數命令輸入時速度跟蹤情況和輸出力矩結果 圖12 力矩為5 N·m條件下正弦低速度函數命令輸入時速度跟蹤情況和輸出力矩結果 圖13 力矩為0.2 N·m條件下正弦高速度函數命令輸入時速度跟蹤情況和輸出力矩結果 圖14 力矩為5 N·m條件下正弦高速度函數命令輸入時速度跟蹤情況和輸出力矩結果 由圖7~圖14可看出,無論是低速還是高速情況下,負載補償能夠比未補償更好地跟蹤速度命令,特別是在初始階段的初始時刻,輸出力矩相對所加初始負載力矩非常小,負載補償能夠使因所加初始負載力矩致使速度產生的負變化更快地變為正值。從整體效果上看,負載補償控制相較未補償時能較快地響應所輸入的速度命令,因此可以避免速度誤差。 本文通過非線性回歸擬合方法對電機運動學方程中的負載慣量、黏性阻尼系數、 負載重力力矩和負載初始位置角度等四個參數進行辨識,從而得到非慣量的負載轉矩。然后對經典電機PI控制方法中的電流環進行前饋轉矩補償,實現對時變負載轉矩的補償。仿真結果驗證了該補償可使速度響應能較快地跟蹤輸入的速度命令,避免了較大速度誤差的出現。




2 負載轉矩補償




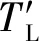




3 仿真分析









4 結 語

