永磁同步電機匝間短路故障匝數診斷方法*

付彥偉, 余建生, 易建波

(1.國能大渡河枕頭壩發電有限公司,四川 樂山 614700;2.電子科技大學 機械與電氣工程學院,四川 成都 611731)

0 引 言

永磁同步電機由于其效率高、轉矩密度大及功率大等特點被廣泛使用。為防止發生系統性乃至災難性的故障,及時診斷出電機故障十分重要。除此之外,及時發現故障可對故障后的應對措施給予指導,避免發生重大損失事故。永磁同步電機的故障主要包括軸承故障、偏心故障、退磁故障和定子故障等,其中匝間短路故障是常見且難以檢測的故障[1]。在電機運行中,熱應力、機械應力、過電流、環境污染以及設備老化等原因均會引起絕緣失效,進而發展為匝間短路故障。根據統計信息,30%的電機故障是由定子繞組故障導致的,同相繞組間發生的短路故障即為匝間短路故障,而80%的電機短路由匝間絕緣故障發展而來[2]。匝間短路故障初期通常發生在少數匝數中,由于短路阻抗很小,因此會產生較大的故障電流,導致局部過熱,進而使繞組之間絕緣進一步被破壞,擴大故障范圍,直至絕緣完全失效,同時還會導致磁體發生不可逆的退磁現象。

永磁同步電機匝間短路故障診斷的方法主要有兩種,一種是通過特征信號[3]進行故障診斷,包括電流、電壓和磁通分析等方式。另一種則是基于模型進行診斷,包括參數的變化以及反電動勢估計器[4]等方式。Yuan等[1]用低正弦電壓激勵靜止狀態下的永磁同步電機,結合響應電流和電機參數計算出短路匝數。文獻[5]直接提取出同相電流和異相電流,分析電流的波動特征,通過對比三相電流波峰值的不平衡度實現對匝間短路的診斷,但是該方法并不能得到短路的匝數,其缺乏對故障嚴重程度的評估。Huang等[6]在考慮到電流控制器對電機模型的影響后,提出了一種新的函數,即通過對不同帶寬的電流和電壓比進行加權,綜合電流和電壓的二次諧波實現故障檢測。在基于小波變換方法的基礎上,文獻[7]以特征頻段系數的均方根作為故障指示進行診斷,獲得了較好的診斷效果,雖然該方法能夠有效發現單匝故障,但是并未證明對不同程度的匝間短路故障能否保持精確性。文獻[8]利用電壓信號的負序分量排除了轉子轉速對結果的影響,故障程度較低時能獲得優于零序分量的診斷效果,但是該方法設定最輕微故障為4%,沒有實現對更早期故障的診斷。Wang等[9]指出在匝間短路故障后,dq軸上的電流、電壓和功率均會產生明顯的二次諧波,因此分別使用有功功率和無功功率的二次諧波對處于發電和負荷狀態下的電機進行診斷。但是Park變換使用的前提是電機對稱,而匝間短路故障建模時,電路非對稱。文獻[10]為了適應匝間短路故障導致的不對稱現象應用相坐標法,在abc坐標系建立模型,將故障后相電流的三次諧波作為故障特征。Wei等[11]則是通過短時Adaline從時變電流信號中提取二次諧波進行檢測。除了單獨使用基波、2次和3次諧波外,文獻[12]融合了定子電流的基波和3次諧波,推導出匝間短路后定子電流會出現5次諧波,并且可以作為故障的有效表征。Wang等[13]使用從發電機收集的定子支路電壓和定子不平衡支路電流作為串聯模型的輸入和輸出信號,采用遞歸批量最小二乘法計算Volterra級數的三個核,通過觀測Volterra內核的改變完成診斷。Mazzoletti等[14]為了避免可能受到的外部干擾帶來的影響和減少誤差診斷,提出了通過測量繞組中點電壓進行診斷的方法。文獻[15]提出了利用改進小波包和快速傅里葉變換處理定子電流信號和振動信號對低速電機進行故障診斷的方法。基于信號的診斷方法中,聯合信號處理的診斷方式能獲得較高的準確率。對電流信號和振動信號同時進行小波變換,可以獲取時頻域中增加的諧波分量作為故障特征。除此之外,文獻[16]中結合了頻域電流、磁通密度和電磁轉矩等多個信號,利用變分自編碼器提取特征并擴充數據的方法,繼而訓練稀疏自編碼器完成故障診斷,但是增加了參數測量成本。除了電信號,還有利用溫度和磁場等信號進行故障分析的方法[17-18],文獻[17]基于磁通分析的方法利用雜散磁通的三次諧波補償磁通基波方法的適用范圍有局限性。文獻[18]采用有限元分析方法,將環境風速和電機散熱性能納入考慮,研究永磁同步電機匝間短路前后的溫升,對試驗與仿真間的誤差作出了合理解釋,但該方法只測試了一種故障匝數情況下的方案準確性。

本文提出的方法不需要添加復雜的測量器件,使用容易獲取的電參數,精確計算短路匝數,直接展示出故障的嚴重程度,為后續計及更多影響因素的故障模型建立打下基礎。在對離線后永磁同步電機匝間短路故障模型進行分析后,完成特征辨識,確定能夠準確計算出故障匝數的特征量,推導出短路匝數計算公式,結合特征量和電機參數完成匝數確定,可用于各種故障程度下的短路匝數計算。

1 電機模型

1.1 故障模型

本文以永磁同步電機為對象,其離線狀態下電路模型為對稱的三相星型電路,其電路圖如圖1所示,由三組電阻電感串聯電路組成。

圖1 永磁同步電機等效模型圖

每一相的阻抗可表示為

Zs=Rs+j2πfLs

(1)

式中:Rs、Ls為永磁同步電機正常狀態下的電阻、電感;f為電路工作頻率。

當永磁同步電機發生匝間短路之后,以A相發生故障為例,電路模型中的故障相將會發生對應的改變,其模型圖如圖2所示。

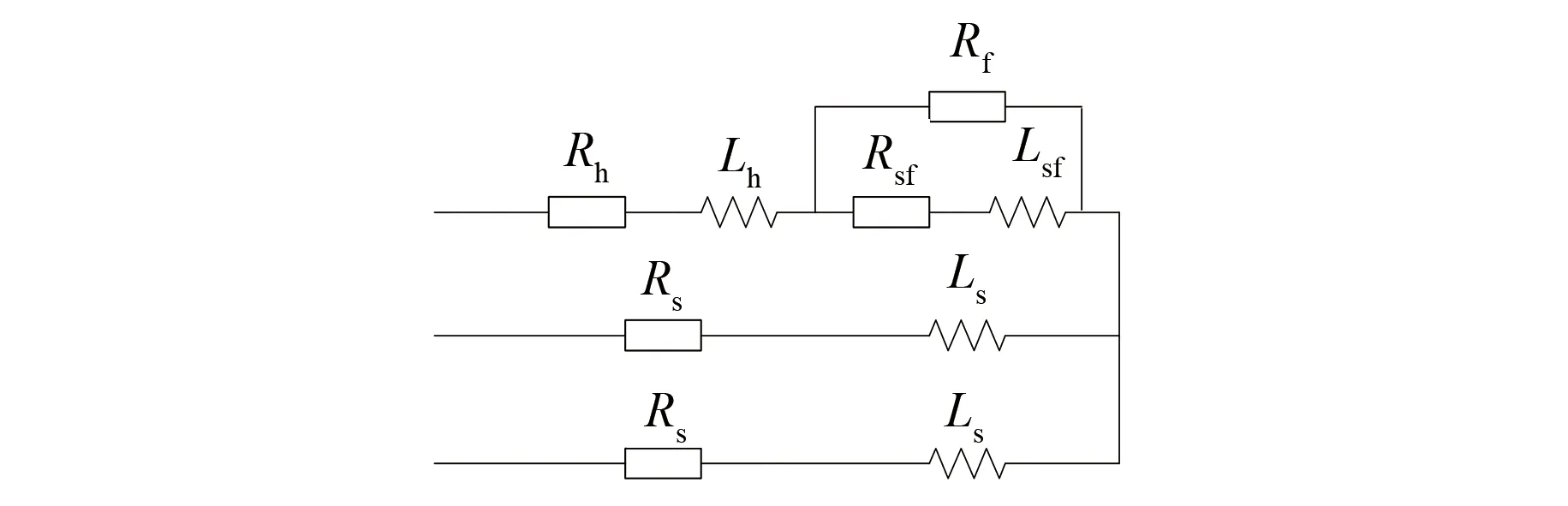
圖2 永磁同步電機無源匝間短路故障模型圖

在故障模型中,正常相(B、C)電路結構并未改變,故障相(A)電路改變為故障部分阻抗與剩余正常部分阻抗串聯,構成了非對稱的三相星型電路。圖2中的各相阻抗表示為

(2)

式中:Rh、Lh分別為故障相中未發生故障的電路部分電阻值、電感值;Rsf、Lsf分別為故障部分電路的正常情況下的參數;Rf為故障后形成的短路支路電阻。

1.2 短路匝數求解計算式推導

得到故障模型后,為推導離線狀態下的短路匝數求解計算式,需構建電壓電流的平衡方程,因此接入單相電壓源作為電路的激勵,其模型圖如圖3所示。

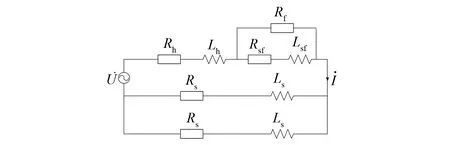
圖3 永磁同步電機有源匝間短路故障模型圖

將未發生故障的兩相并聯,然后與故障相串聯,再將單相電壓源接入之后即得到有源的匝間短路故障模型。在實際運用中,可以采用將三相電路兩兩并聯后再與電源串聯,對干路電流進行測量,獲取三組電流值,其中不同的一組即為圖3所示的電路接線,因此在構建電路過程中可以完成對故障相的定位。

獲得了完整的診斷電路之后,將電壓源的相位、幅值、頻率分別設置為θU、U、f,將由電流互感器測量得到的干路電流的幅值、相位分別命名為θI、I,利用設置及測量得到的參數,結合電機繞組的參數,能夠得到圖3所示電路中的平衡方程為

(3)

假設永磁同步電機發生故障相的故障匝數n與故障相繞組總匝數N的比例為k,即k=n/N。獲得參數k之后,可以列寫出圖3及式(3)中各個參數之間的轉換關系式:

(4)

將式(4)代入式(3)中可以得到新的電壓、電流平衡方程為

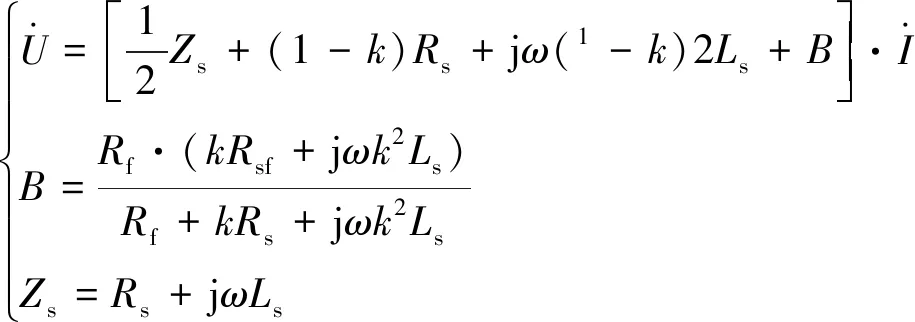
(5)

對式(5)進行變換,得到干路電流的相位與模值為

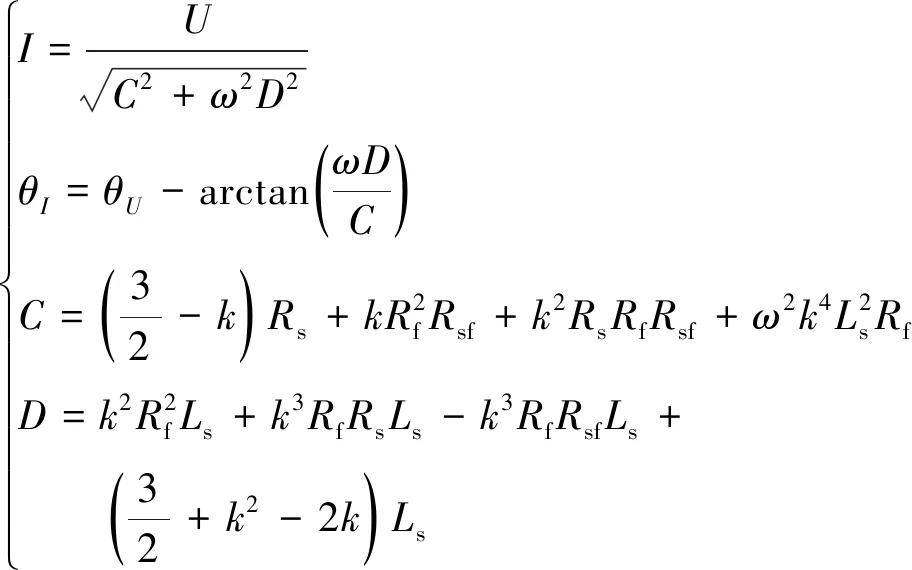
(6)

考慮到實際情況下,短路支路的電阻Rf數值極小,因此在本文中將其數值大小視為零。變換式(6)可以得到干路故障電流的幅值、相位的理論值為

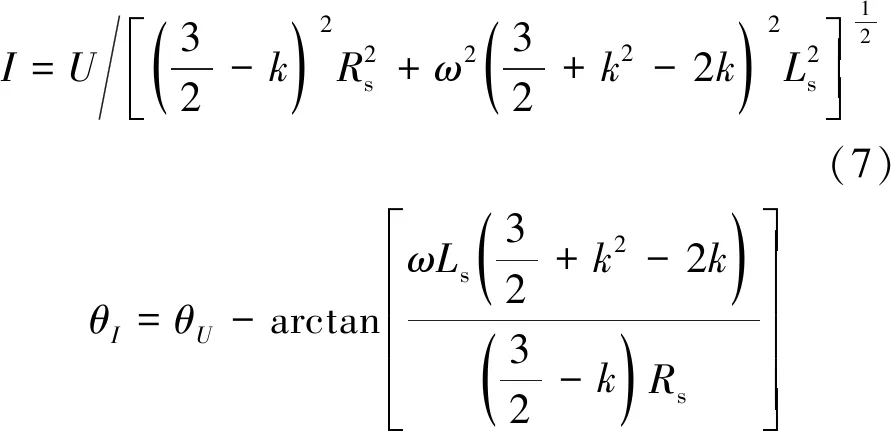
(8)

式(7)、式(8)即為永磁同步電機匝間短路故障模型的電壓、電流平衡方程,其中的未知參數只有匝數短路比k,因此對式(8)進行求解即可得到:

(9)

在式(9)中,計算得到的短路匝數比k為一元二次方程的一組重根,但是實際上k應該是一個固定的準確值,因此需要設定計算值的篩選方案。分析式(7)可以得出結論,當k∈[0,1]時,干路電流模值I是單調遞增的,因此將式(9)得到的一組根代入式(7),得到對應的一組干路電流模值,再與實際測量得到的干路電流模值進行比較驗證,確定唯一的短路匝數比,進而求解N=k*n得到實際的永磁同步電機發生匝間短路的精確匝數。完整的診斷方法流程如圖4所示。

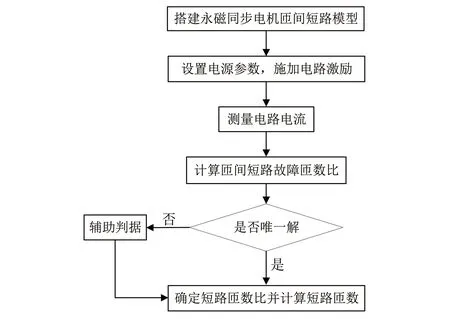
圖4 診斷方案流程圖

2 故障診斷

本文以永磁同步電機為例,通過MATLAB/Sumilink軟件進行電氣仿真,設置電機繞組的電阻值為1.5 Ω,電感值為0.112 H。建立的電路圖如圖3所示,在第一次測試中,設置繞組實際發生短路的匝數比為0.01,將單相交流電壓源的頻率設置為50 Hz,通過函數隨機產生500組電壓相位和電壓幅值,通過本文提出的診斷方法,得到診斷結果如圖5所示。

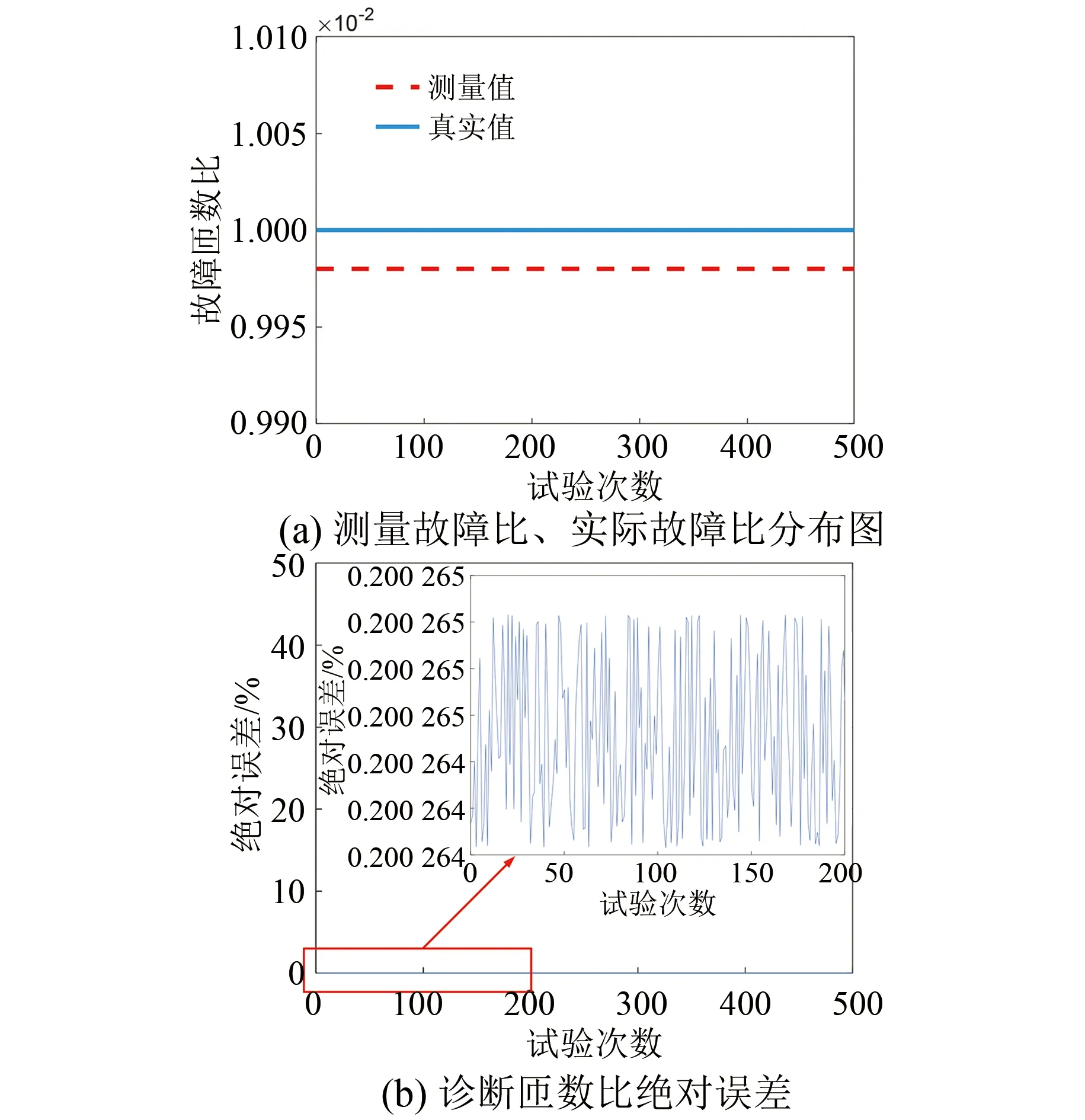
圖5 變電壓診斷結果

根據圖5(a)可知,該方法在匝間短路故障匝數診斷應用上具有良好的可行性與準確性,在電壓源相位發生變化的情況下,測量值對變化的響應幾乎不可見,匝數比測量曲線數值恒定且與實際值誤差控制在10-5的量程內。由圖5(b)知,絕對誤差數值波動的位置處于十萬分位,誤差曲線在數值上不斷波動,但是其數值在一定的區間范圍內。根據式(9)可知,匝數診斷依靠于電壓源與干路電流之間的相位差θ。電壓源幅值的變化,使得電流幅值作出等比例的響應,但對電壓和電流之間的相位差θ沒有影響。電壓源相位的改變會引起電流相位的同步變化,但是因為電路結構和電源頻率沒有發生變化,相位差θ不會發生變化。因此電流電壓源相位和幅值對診斷結果的精度沒有產生影響,試驗符合預期。

為了更全面地驗證診斷方案的可行性和準確性,將試驗條件更改為單相電壓源頻率固定為50 Hz,隨機產生500對電壓相位和電壓幅值,隨機生成故障匝數比,得到的診斷結果如圖6所示。

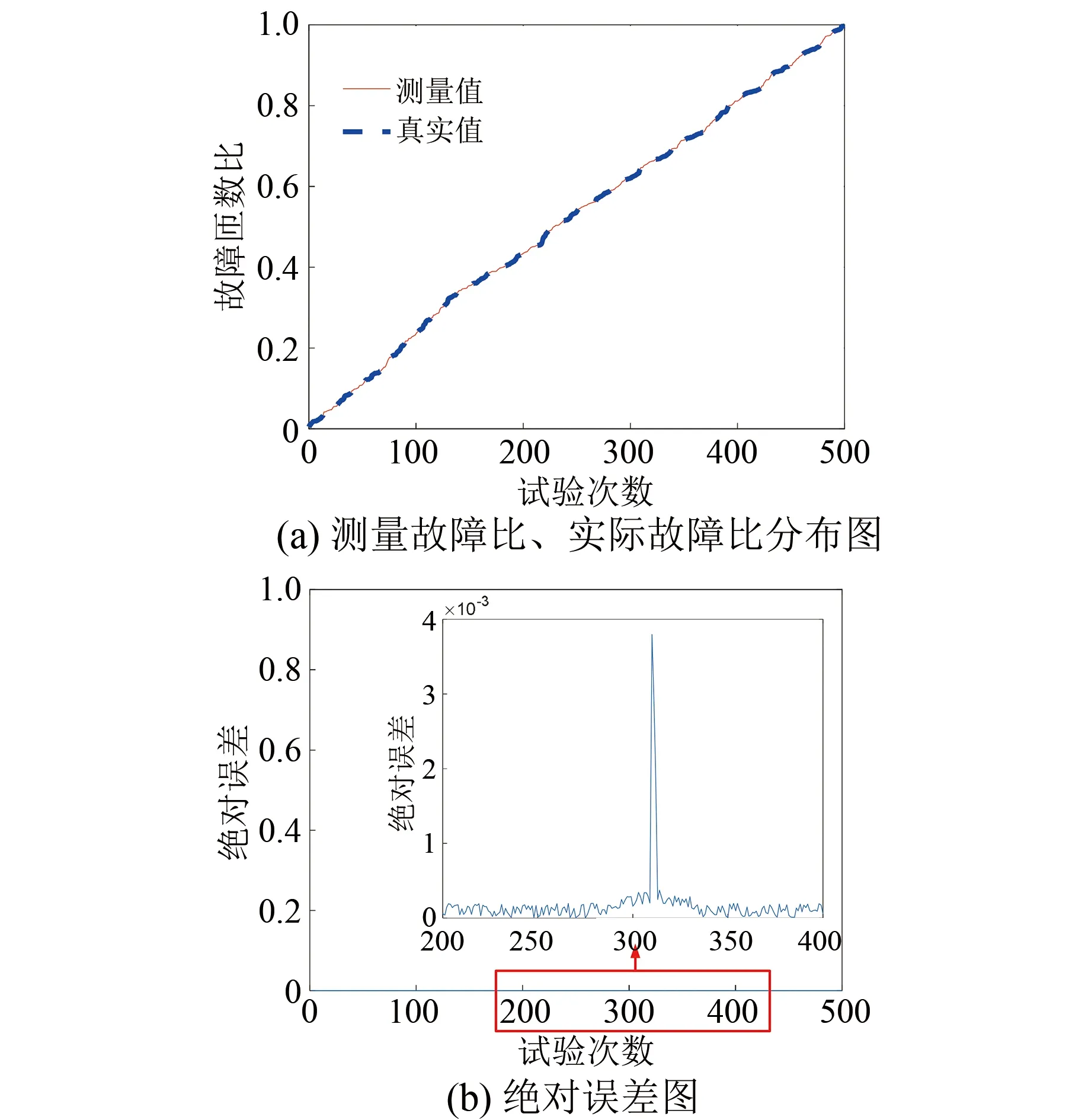
圖6 變故障匝數比診斷結果

從無匝間短路故障開始,逐漸增加短路匝數比,直至繞組全部發生短路時結束。圖6(a)展示了實際的故障匝數比與測量匝數比之間的異同,兩者的變化趨勢和數值大小上近似,證明了該測試條件下診斷方案的可靠性。通過計算得到的實際值和測量值之間的絕對誤差如圖6(b)所示,據圖6(b)可得,兩者的絕對誤差量級為10-3。在絕對誤差曲線中,在第300次測試附近出現了誤差峰值,對于該峰值的出現解釋如下,根據式(9)可知,在全部解集中存在一組相等的根,實際操作中該組根十分接近,因此對式(8)的篩選過程產生影響,導致誤差的增加,但即使是最大誤差也只是10-3的數量級,在宏觀曲線上看,絕對誤差依然近似于0。根據上述分析,本文提出的方法能夠在額定頻率狀態下,對任意匝數發生故障的情況都可作出有效診斷,即能夠實現在故障發生初期對電機的故障程度進行準確地診斷,有效防止故障擴大,避免產生更大的危害。

在上述的仿真分析中,探討了電壓源相位、幅值和故障匝數比對診斷結果的影響,式(9)中電壓源頻率對診斷結果的影響未做評估,因此將試驗條件更改為隨機生成500組電壓相位、電壓幅值、電壓頻率、故障匝數比,在該次試驗中將頻率上限設置為50 Hz,得到的診斷結果如圖7所示。

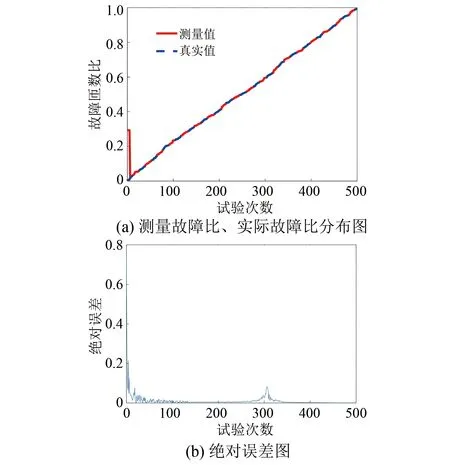
圖7 變頻條件1的診斷結果

由圖7可知,隨著電壓源頻率的增加,測量值和實際值表現出相似的變化趨勢,并且有相近的幅值,絕對誤差基本處于零。誤差曲線中,第300次試驗附近出現的小尖峰原理與圖6中相同。在圖7中,頻率為零時,誤差曲線出現了異常峰值,該現象出現的原因是據式(9),0 Hz的電壓源導致方程中出現了分母為零的項,在計算過程中產生了無限大的數值,導致誤差出現在電路層面上,當電源頻率為零后,繞組電感特性被忽略,改變了電路結構。而在實際運用中,交流電壓源的頻率不會為零,因此該誤差對本文提出的診斷方法的準確性不會產生影響。

為了進一步驗證在更大范圍區間內的電源頻率變化對診斷結果的影響,將上訴試驗條件中頻率上限的50 Hz更改為500 Hz,再次試驗后得到的診斷結果如圖8所示。

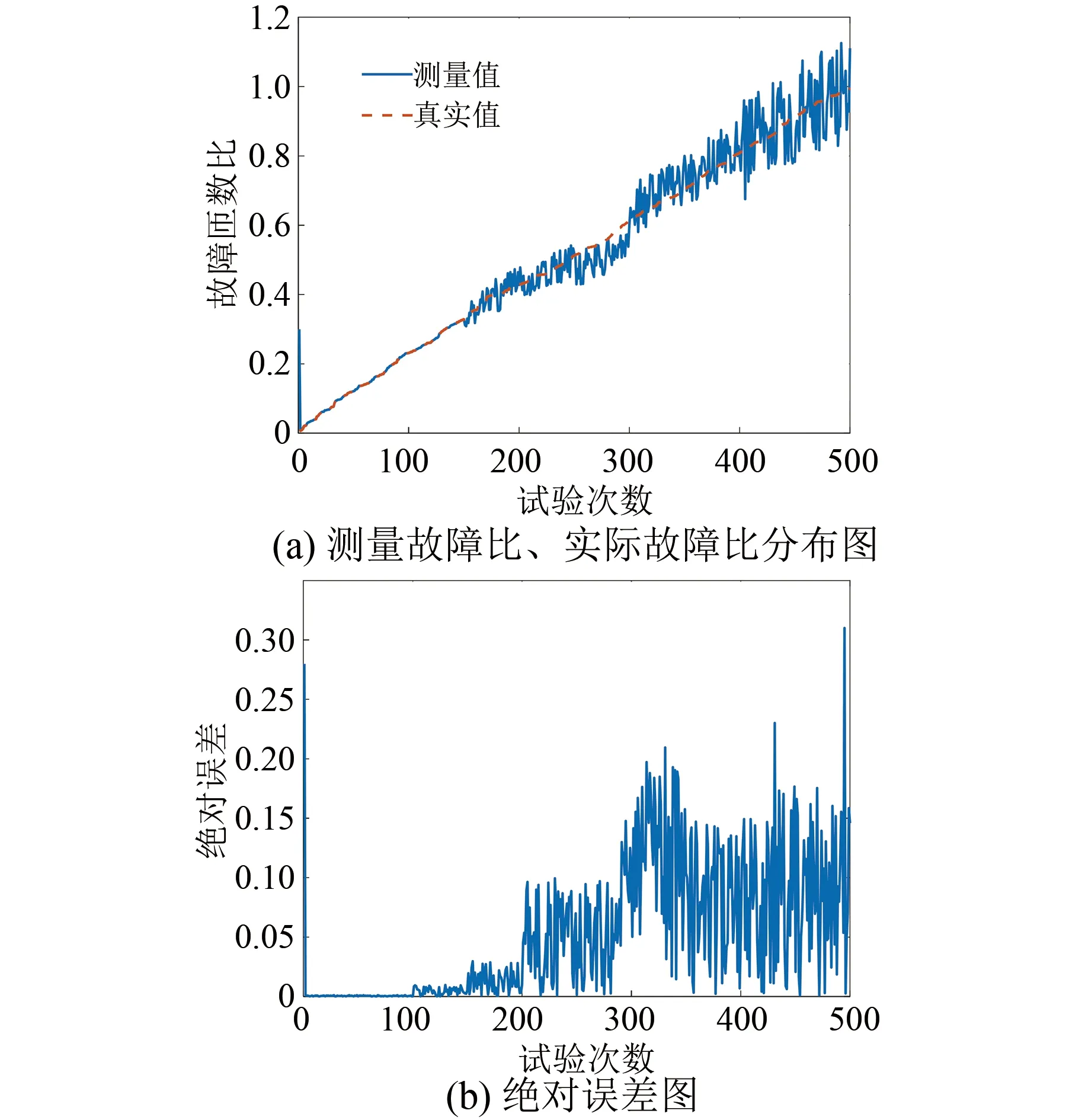
圖8 變頻條件2的診斷結果

在圖8中,當電壓源頻率不超過200 Hz時,測量值曲線和實際值曲線在除零點外的區域幾乎一致,在電壓源頻率超過200 Hz后,測量值呈現不規則的鋸齒波形,同時曲線出現隨機分布的趨勢,診斷的準確性下降。在絕對誤差曲線中表現為,頻率大于200 Hz后誤差幅值大幅度變化,峰值急劇上升。原因是據式(9)中,當頻率增加之后,電路的電阻、電感以及壓流相位差對診斷結果的影響將會被極大的角速度弱化,導致匝數比由角速度起決定性作用,使匝數k的求解結果逐漸退化為一對共軛的虛數根,對應電路即為電路向感性偏移,電阻的影響減小,電路結構不再如同圖3所示,因此電壓頻率過大導致的準確率下降是合理的。但是在實際運用中,單相交流電壓源的頻率可以在一定的范圍內進行調整,而圖8可以論證即使是100 Hz的電壓源,本文的診斷方法仍能保持較高的準確率,因此在實際運用中不會出現由于電壓頻率導致的診斷缺陷情況。

3 結 語

本文提出了利用電機模型的電氣特征量對離線狀態下的永磁同步電機匝間短路故障下短路匝數的診斷方法,可以確定故障相位置,對低匝數故障的診斷有較高的準確性。通過仿真分析可知,該方法可以在寬泛的電源頻率、任意電壓相位、幅值的條件下,對各種程度的匝間短路故障進行故障匝數的準確計算。仿真結果表明,電壓源相位、幅值的變化不會對診斷結果的準確率產生影響,當電壓源頻率大于零且不超過200 Hz時,診斷的準確率能夠保持在較高水平,不超過100 Hz時能夠得到最佳的診斷效果,當頻率大于200 Hz后,由于同步電機的電路特性,診斷結果將不再具備穩定性和準確性,因此在應用中需要對電壓源的頻率進行限制。在電壓源頻率適當的情況下,該模型對發生各種程度匝間短路故障的匝數都可以進行準確地計算。

本文提出的利用電機模型的電氣特征量對離線狀態下的永磁同步電機匝間短路故障的短路匝數的診斷方法不需要添加復雜的測量器件,使用容易獲取的電氣參數,能準確計算出短路匝數,從而直接展示出故障的嚴重程度。