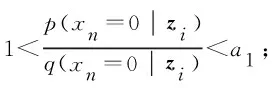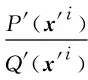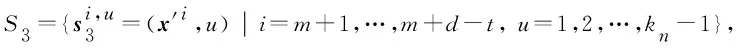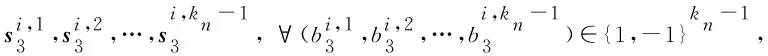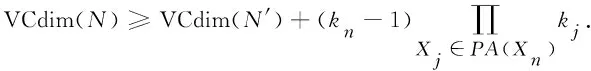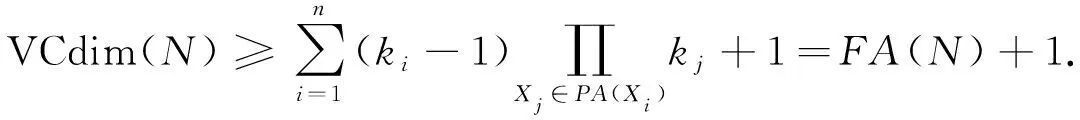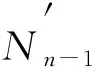離散Bayes網誘導的概念類VC維數的下界

羅亭亭, 李本崇

(西安電子科技大學 數學與統計學院, 西安 710126)

Bayes網絡[1], 也稱為概率網絡、 信念網絡或者因果網絡, 是一種用有向無環圖表示隨機變量間條件獨立關系的統計模型, 最初主要用于處理人工智能中的不確定性信息, 目前廣泛應用于不確定性推理和機器學習等領域[2-6]. Bayes網絡通過若干條件分布的乘積表示復雜的聯合概率分布, 因此有助于處理高維統計問題.

VC(Vapnik-Chervonenkis)維數和歐氏嵌入維數是二值函數類復雜性的兩種度量[7], 離散Bayes網絡誘導的概念類的VC維數和歐氏嵌入維數的大小備受關注. Kearns等[8]研究了一般概念學習的形式化模型, 著重研究了概念類的可學習性和一致收斂性, 并給出了許多有效算法; García-Puente等[9]給出了離散Bayes網的代數幾何刻畫; Nakamura等[10]給出了二值隨機變量Bayes網誘導的概念類歐氏嵌入維數的上下界, 并確定了一些特殊Bayes網誘導的概念類歐氏嵌入維數的精確值; Yang等[11-12]針對Boolean域上的二分類任務, 證明了完全Bayes網和幾乎完全Bayes網誘導的概念類的VC維數和歐氏嵌入維數相等; Yang等[13]針對隨機變量取值均為k個的二分類問題, 證明了任意不含有V-結構的Bayes網誘導的概念類VC維數和歐氏嵌入維數的一致性, 并給出了計算該維數的顯示公式; Yang等[14]針對變量在Boolean域取值的Bayes網, 證明了隨機變量個數不超過5時, Bayes網絡誘導的概念類的VC維數與歐氏嵌入維數相等; Varando等[15]用Lagrange多項式乘積的線性組合評估Bayes網的表達能力, 得到了與文獻[13]類似的結果; Li等[16]擴展了Yang等[13]以及Varando等[15]的結果, 證明了任意不含V-結構的Bayes網誘導的概念類VC維數和歐氏嵌入維數的一致性, 并給出了一般Bayes網誘導的概念類歐氏嵌入維數的上界(VC維數的上界). 近年來, 研究者們已利用Bayes網絡模型解決了許多實際問題[17-19], 但對Bayes網誘導的概念類的復雜性理論研究目前尚未見文獻報道. 當一個網絡中的每個隨機變量取任意有限個值時, 該Bayes網絡誘導的概念類VC維數的下界尚無一般性結果. 因此, 基于Yang等[13]的工作, 本文考慮一般的離散Bayes網絡誘導的概念類VC維數的下界, 為進一步研究Bayes網誘導的概念類的復雜性做鋪墊, 并為分類任務提供理論支撐.

1 預備知識

定義1[1]如果一個有向圖從任意頂點出發, 沿任意若干條有向邊都不能回到該點(不含有向環), 則稱該圖是一個有向無環圖, 記作G=(V,E).每個頂點Xi∈V表示一個隨機變量, 一個有向邊(Xi,Xj)∈E表示Xi和Xj之間的條件依賴性, 其中V={X1,X2,…,Xn},i,j∈{1,2,…,n}且i≠j.

圖G中若(Xi,Xj)∈E, 則Xi稱為Xj的父節點,Xj稱為Xi的子節點.本文用PA(Xi)表示節點Xi的父節點集合,mi=|PA(Xi)|表示父節點的個數.一個有向圖是完全的當且僅當給定節點的拓撲序時, 對每個節點Xi都有PA(Xi)={X1,X2,…,Xi-1}.令X,Z,Y是有向無環圖G=(V,E)的3個節點, 如果G中包含有向邊X→Z和Y→Z, 且X和Y在G中不相鄰, 則稱(X,Z,Y)是一個V-結構, 如圖1所示.

圖1 圖G的一個V-結構Fig.1 A V-structure of graph G

每個有向無環圖G都對應一個概率分布族P,P由X上有如下形式的概率分布組成:

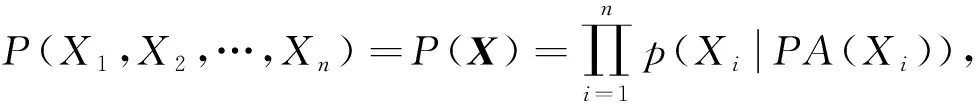
(1)

其中p(Xi|PA(Xi))表示給定父變量PA(Xi)時Xi的條件概率.

定義2(Bayes網)[2]一個Bayes網由有向無環圖G=(V,E)和分布族P構成, 記作N=(G,P).

例1如圖2所示的一個有向無環圖, 節點集V={X1,X2,X3,X4}, 有向邊集合E={(X1,X2),(X1,X3),(X2,X4),(X3,X4)}.由式(1)可知, 該有向無環圖對應的概率分布族中的每個分布P滿足

圖2 一個有向無環圖Fig.2 A directed acyclic graph

P(X)=p(X1)p(X2|X1)p(X3|X1)p(X4|X2,X3).

考慮N是一個有n個節點X1,X2,…,Xn的Bayes網,Xi∈[ki], 其中ki∈,ki≥2,i=1,2,…,n.易知若PA(Xi)={Xi1,Xi2,…,Xir}, 觀測向量為x=(x1,x2,…,xn), 則xpa(xi)?(xi1,xi2,…,xir).將N對應的分布族記為DN,DN中X上的任一概率分布由如下形式表示:

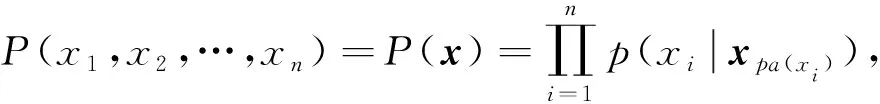
(2)

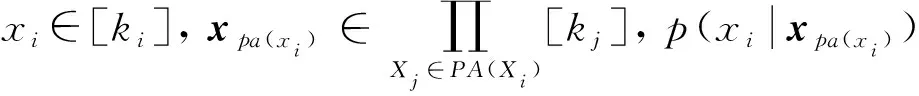
記Bayes網絡N可自由設定的參數個數為FA(N), 基于上述討論可知參數個數應為所有變量可自由設定的參數數目之和, 即

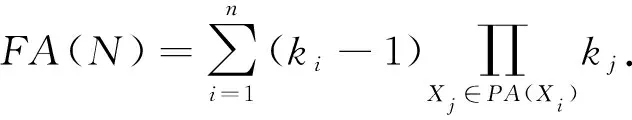
(3)

根據式(3), 對完全的Bayes網絡NF, 其可自由設定的參數個數為

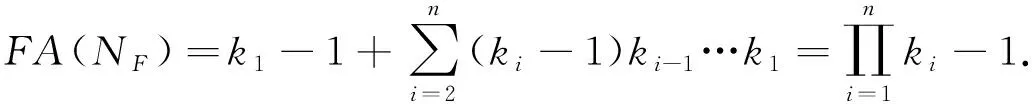
(4)

例2以圖2對應的Bayes網絡為例,X=(X1,X2,X3,X4),Xi取ki個值,i=1,2,3,4.若x=(1,0,1,2), 則由PA(X4)={X2,X3}可得xpa(x4)=(0,1).若變量X1,X2,X3,X4對應的可自由設定參數個數分別為k1-1,k1(k2-1),k1(k3-1),k2k3(k4-1), 則由式(3)可得該Bayes網絡的可自由設定參數個數為k1-1+k1(k2-1)+k1(k3-1)+k2k3(k4-1).

定義3[10]概念類C是定義在X上的一個函數族, 滿足f:X→{-1,1}, 每個f∈C稱為一個概念.

定義4[10]一個有限集合S={s1,s2,…,sm}?X稱為被概念類C打散是指對任意m維向量b∈{-1,1}m, 存在f∈C使得f(si)=bi, 其中i=1,2,…,m.

定義5[10]概念類的VC維數定義為

VC dim(C)=sup{m|S?X,S被C打散, 且|S|=m}.

(5)

若由任意數目的樣本點組成的集合都能被概念類C打散, 則該概念類的VC維數即為無窮大.

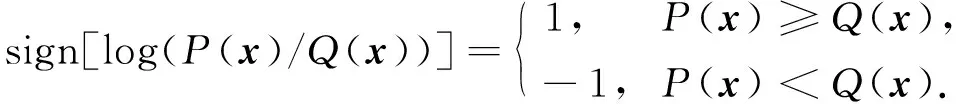
(6)

由定義5和定義6可得Bayes網誘導的概念類的VC維數, 將CN的VC維數記作VCdim(N).歐氏嵌入維數是用來評價Bayes網分類能力的另一個常用指標, 其定義如下:

定義7[10]給定X上的一個概念類C和一個具有標準內積的d維歐氏空間, 若存在d中的向量(uf)f∈C和(vx)x∈X, 使得?f∈C,x∈X, 有則稱概念類C可以嵌入到d維歐氏空間.使C可以被嵌入d中最小的d稱為概念類C的歐氏嵌入維數, 記作Edim(C).

對于一個概念類C, 如果不存在有限維的歐氏空間可以被C嵌入, 則Edim(C)為無窮大.概念類CN的歐氏嵌入維數記作Edim(N).

例3考慮圖2對應的Bayes網, 若Xi∈{0,1},i=1,2,3,4, 則VCdim(N)=Edim(N)=11[12].

命題1[10]對每個有限概念類C, 均有Edim(C)≥VCdim(C).

命題1表明,CN的歐氏嵌入維數是其VC維數的上界.完全Bayes網絡誘導的概念類的VC維數和歐氏嵌入維數皆等于網絡中可自由設定的參數個數[20].

命題2[13]設N′是有(n-1)個變量的Bayes網絡,N中有向無環圖去掉節點Xn及與之相連的有向邊后對應的Bayes網為N′, 若S′?[k]n-1被N′打散且VCdim(N′)=|S′|, 則

VCdim(N)≥VCdim(N′)+(k-1)k|PA(Xn)|,

(7)

其中Xi∈[k],i=1,2,…,n.

命題2表明, 一個有n個k-值隨機變量的Bayes網絡誘導的概念類VC維數的下界是前(n-1)個變量組成的Bayes網絡誘導的概念類VC維數與最后一個變量對應的可自由設定的參數個數之和.

定理1[13]設N是一個離散的非完全Bayes網絡, 其有n個變量X1,X2,…,Xn, 且每個變量Xi∈[k],k∈,k≥2, 則

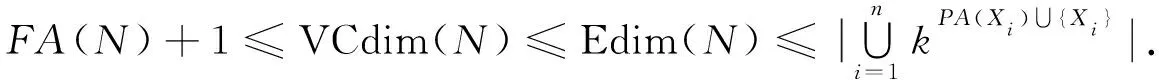
(8)

定理2[16]設N是一個有n個隨機變量, 無V-結構的非完全Bayes網絡, 且每個變量Xi∈[ki],ki∈,ki≥2, 則

VCdim(N)=Edim(N)=FA(N)+1.

(9)

定理1給出了當隨機變量取值個數均為k時, 非完全Bayes網絡誘導的概念類VC維數和歐氏嵌入維數的上下界.定理2表明, 不含有V-結構的非完全Bayes網誘導的概念類的VC維數和歐氏嵌入維數相等.

2 概念類VC維數的下界

Yang等[13]證明了當X=(X1,X2,…,Xn)在[k]n上取值時, 非完全Bayes網中得到的VC維數的下界為可自由設定的參數加1.本文推廣該結果, 考慮網絡中每個隨機變量Xi∈[ki](ki∈,ki≥2)時該Bayes網誘導的概念類VC維數的下界.

首先給出一個引理, 其本質是在定義Bayes網誘導的函數類時, 若函數類中不包含(1,1,…,1), 則可改寫符號函數的定義, 以避開樣本點概率相等的情形.

引理1設N是有n個變量X1,X2,…,Xn的Bayes網絡, 其中Xi∈[ki],ki∈,k≥2,i=1,2,…,n,N誘導的概念類為CN, 則對每個k1k2…kn維的向量b=(b1,b2,…,bk1k2…kn)∈CN-{(1,1,…,1)}都存在一對分布P,Q∈DN, 使得:

1) sign[log(P(xk)/Q(xk))]=bk;

證明: 當n=1時,N是一個完全Bayes網絡, 此時的結果是文獻[13]中引理3.4的一個特例, 因此當n=1時結論成立.

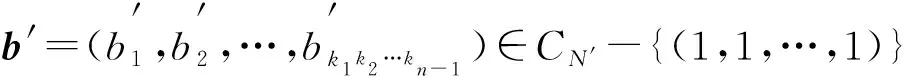
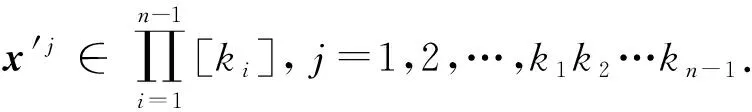
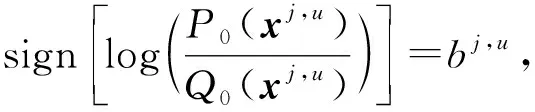
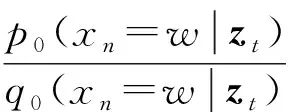
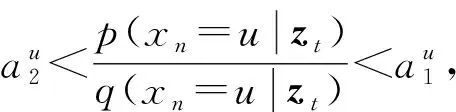
命題3[13]設a是一個非負實數,b是一個m維向量, 其中

b=(b1,b2,…,bm)∈({1,-1}m-{(1,1,…,1),(-1,-1,…,-1)}),

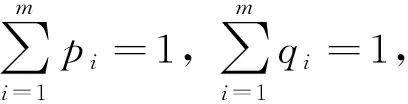
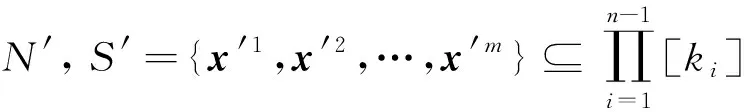
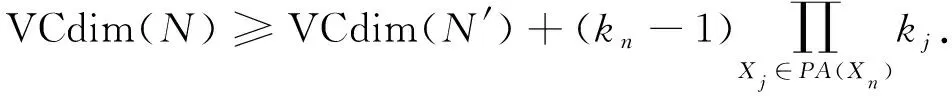
(10)

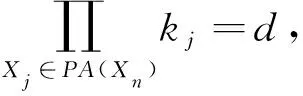
{x′m+1|PA(Xn),x′m+2|PA(Xn),…,x′m+d-t|PA(Xn)}={zt+1,zt+2,…,zd},

且zt+1,zt+2,…,zd均不相同, 其中zt+1,zt+2,…,zd都是r維的.取

S3={(x′i,1),(x′i,2),…,(x′i,kn-1)|i=m+1,…,m+d-t},

易知S1∩S2=?,S1∩S3=?,S2∩S3=?.現令S=S1∪S2∪S3, 則有

下面證明?b=(b1,b2,…,bm,bm+1,…,bm+d(kn-1))∈{1,-1}m+d(kn-1), 存在一對分布P,Q∈DN, 使得

sign[log(P(si)/Q(si))]=bi,i=1,2,…,m+d(kn-1),

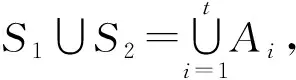
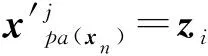
① (bi,0,bi,1,…,bi,kn-1)∈{(1,1,…,1),(-1,-1,…,-1)}, (bj1,0,…,bjl,0)∈{1,-1}l.

首先考慮si,0,si,1,…,si,kn-1, 可以指定參數p(xn=u|zi)=q(xn=u|zi), 選擇分布P′,Q′只需滿足P′(x′i)≥Q′(x′i)或P′(x′i)

② (bi,0,bi,1,…,bi,kn-1)∈{1,-1}kn-{(1,1,…,1),(-1,-1,…,-1)}, (bj1,0,…,bjl,0)∈{1,-1}l.

首先考慮si,0=(x′i,0)∈Ai, 由引理1知, 若bi,0=1, 則選擇分布P′,Q′時需滿足P′(x′i)>Q′(x′i); 若bi,0=-1 , 則選擇分布P′,Q′時需滿足P′(x′i)Q′(x′j); 若bj,0=-1, 則選擇分布P′,Q′時需滿足P′(x′j)

引理2是命題2的推廣, 它表明當Bayes網絡中每個隨機變量取任意有限個值時, 該網絡誘導的概念類的VC維數大于或等于前(n-1)個變量組成的Bayes網絡誘導的概念類的VC 維數與最后一個變量的可自由設定參數個數之和.在引理2的基礎上, 結合定理2, 有下列結論.

定理3設N是一個有n個節點X1,X2,…,Xn的非完全Bayes網絡, 其中Xi∈[ki],ki∈,ki≥2, 則

(11)

證明: 當n=1時,N1是一個完全Bayes網絡, 此時VCdim(N1)=FA(N1)=k1-1[13,16].考慮非完全Bayes網從n=2開始, 由定理2知, VCdim(N2)=k1+k2-1,FA(N2)=k1+k2-2, 結論成立.

假設該結論對任一有(n-1)個變量X1,X2,…,Xn-1的非完全Bayes網Nn-1成立, 且Xi∈[ki], 則

證畢.

定理3給出了所有離散非完全Bayes網誘導的概念類VC維數的下界, 對此說明如下.

(i) 當Bayes網絡不含有V-結構時, 此類Bayes網誘導的概念類VC維數的下界正是VC維數[16].

(ii) 當Bayes網絡含有V-結構時, 有些情況下這個下界恰為VC維數.例如, 圖1所示的有向圖對應的非完全Bayes網絡, 令X,Y,Z∈{0,1}, 則該Bayes網絡的可自由設定參數個數為1+2×2+1=6, 其誘導的概念類VC維數的下界為6+1=7, 這與Yang等[14]證明的該Bayes網誘導的概念類VC維數等于7一致.

(iii) 在Bayes網絡含有V-結構時, 這個下界有時偏小. 例如, 圖2對應的Bayes網絡含有一個V-結構, 當X1,X2,X3,X4∈{0,1}時, 該Bayes網誘導的概念類VC維數的下界為1+2+2+4+1=10, 而Yang等[12]證明了該Bayes網誘導的概念類VC維數為11.

綜上所述, 本文主要討論了一般Bayes網誘導的概念類VC維數的下界問題. 對每個隨機變量都可取任意有限值的任一非完全Bayes網絡, 考慮其誘導的概念類的VC維數與網絡中可自由設定的參數個數的關系, 證明了任意非完全離散Bayes網的可自由設定參數個數加1后, 是該Bayes網誘導的概念類VC維數的一個下界. 對于沒有V-結構的非完全Bayes網絡, 本文給出的這個下界恰好是VC維數[16]; 對于含有V-結構的非完全Bayes網絡, 這個下界可能等于VC維數, 也可能小于VC維數. 本文的研究結果對任一非完全Bayes網絡都適用, 解決了一般Bayes網誘導的概念類VC維數的下界問題, 為進一步研究Bayes網誘導的概念類的復雜性提供了參考.