拉伸和彎曲載荷作用下含R槽方形殼角裂紋應力強度因子計算

李 龍

（西安科技大學 建筑與土木工程學院，西安 710054）

0 前 言

通常，對于無限大二維及三維彈性體裂紋問題，給出應力強度因子的解析解是相對容易的。對于帶有邊界裂紋問題的求解，相關文獻給出了裂紋非自發擴展的能量釋放率的概念及其積分定義[1]以及在圓柱管殼[2]、薄壁等邊角鋼[3]等裂紋中的應用。但當考慮裂紋尖端有多個不同的奇異應力場和應力強度因子的裂紋問題，若想給出滿足條件的解析解是相對困難的。因此，許多學者對求解含裂紋工程構件的應力強度因子的方法進行了相關研究。文獻[4-5]基于J2守恒積分和虛功原理提出了求解多個不同奇異應力場對應的應力強度因子的方法。但大部分的梁和細長工程構件上裂紋的產生是多個荷載共同作用的結果，所以目前求解構件上裂紋截面受到拉伸和彎曲載荷作用且具有多個不同的奇異應力場和應力強度因子的裂紋問題主要依賴于有限元法。如果能找到拉伸和彎曲載荷之間的一些關系，則J2積分可以繼續在求解拉伸和彎曲載荷共同作用下多個不同奇異應力場對應的應力強度因子中發揮作用。

本研究基于J2積分和材料力學中截面應力分析理論[6]，以含R 槽方形殼對稱穿透角裂紋應力強度因子為例，通過找出兩種荷載之間的簡單關系，求解拉伸和彎曲荷載作用下不同應力場裂紋尖端應力強度因子，建立拉伸和彎曲荷載共同作用下含R槽方形殼對稱穿透角裂紋應力強度因子的計算方法。

1 含R槽方形殼對稱穿透角裂紋構型

本研究以含對稱穿透角裂紋的R槽方形殼為例，重點研究拉伸和彎曲載荷作用下對稱穿透角裂紋的應力強度因子求解問題。假設在角裂紋橫截面上，存在4組對稱穿透角裂紋，如圖1所示。先以彎曲載荷為例，給出彎曲載荷作用下不同裂紋尖端應力強度因子的計算方法，隨后在此基礎上進一步研究拉伸和彎曲載荷共同作用下不同裂紋尖端應力強度因子的計算方法。

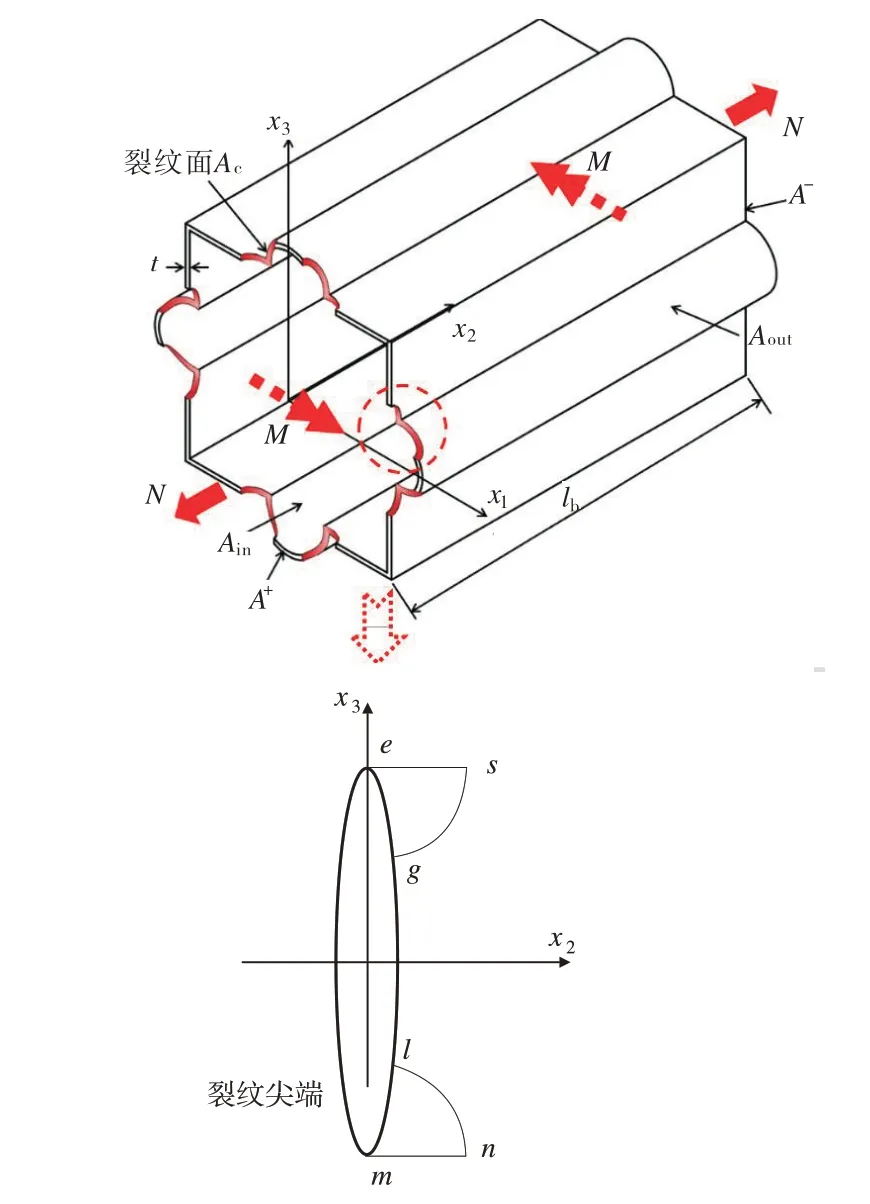
圖1 含R槽方形殼對稱穿透角裂紋構型

2 J2積分法計算R 槽方形殼對稱穿透角裂紋應力強度因子

2.1 三維J2積分

考慮三維位移場，其位移矢量μ是x1、x2和x3的函數，對于閉合曲面Ω，根據守恒律，公式（1）的積分為0[7-8]，即

式中：w——應變能密度，J/mm3；

Ti——作用于Ω外側面的力矢量，N；

nj——曲面Ω的外法線矢量；

ui,j——位移矢量，mm。

含R 槽方形殼的對稱穿透角裂紋如圖1 所示。當x2軸與裂紋截面垂直，三維J2積分可用于求解拉伸和彎曲載荷作用下含R槽方形殼角裂紋的應力強度因子。

2.2 二維J2積分

對于二維邊值問題，守恒律仍保持公式（1）的形式。這時公式（1）中的積分路徑為s，是坐標x1-x2平面內的一條閉合曲線。該積分在這樣的不含孔洞閉合曲線上的積分值為0，即

單位厚度的I 型裂紋如圖1 所示。在裂紋尖端近場取閉合積分路徑，計算方法為

式中：ses——裂紋尖端的直線段；

ssg——四分之一圓弧段；

sge——裂紋面。

沿著路徑ses和ssg，J2積分可表示為

對于閉合路徑s=sesg+seg，公式（2）可表示為

式中：μ——泊松比；

E——彈性模量，MPa；

KI——I型應力強度因子，MPa·m1/2。

3 彎曲載荷作用下含R 槽方形殼對稱穿透角裂紋的應力強度因子

帶有對稱穿透角裂紋的含R槽方形殼如圖1所示。僅考慮彎曲作用時，x1-x3平面為含裂紋的對稱平面，所有載荷均作用在該平面上，同時變形也將發生在這個平面。顯然，當滿足lb>>t時，含R槽方形殼的形變具有細長梁構件和三維殼體的特征。可以將材料力學中的應力與變形計算方法應用于含R槽方形殼角裂紋的應力強度因子的計算。

3.1 閉合積分曲面

如圖1 所示，含R 槽方形殼在裂紋截面遠場受彎曲載荷作用。選取三維閉合曲面Aclosed=A++A-+Ain+Aout+Ac，其中符號“+”表示裂紋截面，“-”表示遠場截面，A+為裂紋韌帶截面，A-為遠場無裂紋截面，Ain為含R槽方形殼的內側表面，Aout為含R槽方形殼的外側表面，Ac為裂紋面。因為Ain和Aout為自由面，Ti= 0、n2= 0，因此可得如下結果[9]

對于積分曲面A+和A-，不難得到

?′——含R槽方形殼的軸線曲率。

式中：I——慣性矩，mm4，I=(B-2R)[B3+t(B-2R)2]/6+B2t(B-2R)/4+4Rt(π-α)-at3/3-atB2；

R——含R槽方形殼的半圓半徑， mm；

M——作用于含R槽方形殼兩端彎矩， N?m。

將裂紋看成由橢圓孔d′→0 時退化而成，于是含R 槽殼可看成一變截面管，如圖2 所示。裂紋處的軸線曲率可由下列極限求得

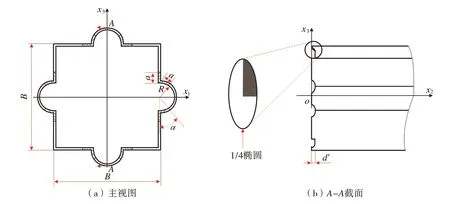
圖2 1/4裂紋橢圓模型（d′→0）

式中：d′——橢圓裂紋模型的短半軸長度，mm；

a——橢圓裂紋模型的長半軸長度，mm；

B——含R槽方形殼截面相鄰直角間距，mm；

t——含R槽方形殼厚度，mm；

γ1——以a/B為自變量的函數。

圖1中裂紋面Ac由八個裂紋面組成，其局部放大如圖3所示。

圖3 K主導區域內的局部積分面

根據能量守恒定律，在裂紋面Ac上，有

式中：J2(Aml) ——裂紋面ml上的J2積分，N/m；

J2(Aeg) ——裂紋面eg上的J2積分，N/m；

KIm、KIe——裂紋面ml、eg 上的應力強度

因子，MPa·m1/2。

結合公式（14）和公式（15），在裂紋面Ac上有

將公式（8）～公式（10）和公式（16）代入公式（1），Aclosed=A++A-+Ain+Aout+Ac上的J2積分可表示為

3.2 補充方程

如公式（17）所示，是一個包含多個不同應力強度因子的方程，由文獻[10-12]可知，裂紋尖端e和m處不同應力強度因子相互關系的補充方程為

式中：R——含R槽方形殼的半圓半徑，mm；

a——橢圓裂紋模型的長半軸長度，mm；

α——彎曲載荷作用下含R 槽方形殼裂紋尖端與R 槽方形殼圓心的連線與x3軸之間的夾角，（°）。

3.3 正則化應力強度因子

將公式（11）、公式（12）、公式（18）代入公式（17），可得含R 槽殼的兩種應力強度因子分別為

式中：fe(a/B) ——含R 槽方形殼在裂紋尖端e處的應力強度因子，MPa·m1/2；

fm(a/B) ——含R 槽方形殼在裂紋尖端m處的應力強度因子，MPa·m1/2；

σ0——含R 槽方形殼截面應力，kPa，本研究中

4 拉伸、彎曲載荷共同作用下含R 槽方形殼對稱穿透角裂紋的應力強度因子

4.1 基于G積分的裂紋擴展能量釋放率

根據G積分理論，含R 槽方形殼應變能表達式為

式中：G——基于G積分的裂紋擴展能量釋放率，N/m。

公式（21）的物理意義為裂紋面Seglm在x2方向上每平移單位距離時的能量釋放率或裂紋面擴展的能量釋放率。

4.2 基于彎曲理論的裂紋擴展能量釋放率

將含R 槽殼看做桿件結構，根據材料力學中的梁彎曲理論，可得含R 槽殼應變能表達式為

式中：U——基于彎曲理論的裂紋擴展能量釋放率，N/m；

N——作用于含R 槽方形殼兩端的拉伸載荷，N;

lb——含R槽方形殼的長度，m；

式中：φ——拉伸、彎曲載荷作用下含R 槽方形殼裂紋尖端與R 槽方形殼圓心的連線與x3軸之間的夾角，（°）；

γ1——裂紋截面的面積因子。

4.3 補充方程

從公式（22）不難發現，公式中同時含有彎矩M和軸向拉力N。眾所周知，在做構件彎曲試驗時常采用三點彎加載，在構件的底部中心微小范圍內構件可近似看成局部受拉，基于此思路，借助材料力學中截面應力分析理論，對拉伸和彎曲載荷共同作用下的含R 槽方形殼進行應力分析，可以得到，在拉伸和彎曲載荷作用下構件上裂紋尖端處所受彎矩與軸力的關系[5]可近似表示為

式中：M——作用于含R 槽方形殼兩端的彎矩，N?m；

I——慣性矩，mm；

N——作用于含R 槽方形殼兩端的拉伸載荷，N;

B——含R 槽方形殼截面相鄰直角間的距離，mm。

由季札的評論我們可知《唐風》的特點：一是思深； 二是憂遠； 三是有傳統，有歷史感。 思深和憂遠意思相近，故杜預概括為憂深思遠，而有傳統、有歷史感又是和憂深思遠相聯系著的。 因此，若從風格上講，可以說是厚重感。 若從思想上來講，可以說是計長遠。 對于《唐風》，可以如此把握之。

4.4 正則化應力強度因子

根據Clapeyron 理論，外載荷作功V=2U，內能Π=U-V=-U，根據平衡條件，則裂紋能量釋放率可表示為

式中：γ1(α/π,t)——以α/π、t為變量的裂紋截面的面積因子；

γ2(α/π,t)——以α/π、t為變量的裂紋截面的慣性因子。

正常條件下，兩種計算方法得到的能量釋放率相同，因此有

將公式（26）代入公式（30），可得m點處正則化應力強度因子為

公式（31）給出了一個估算對稱穿透角裂紋應力強度因子的公式，在該公式中，含R槽方形殼上角裂紋尖端的應力強度因子僅取決于裂紋截面上的彎矩。因此，使用該方法來表示拉伸和彎曲載荷作用下類似含裂紋殼的應力強度因子成為可能。

5 有限元分析

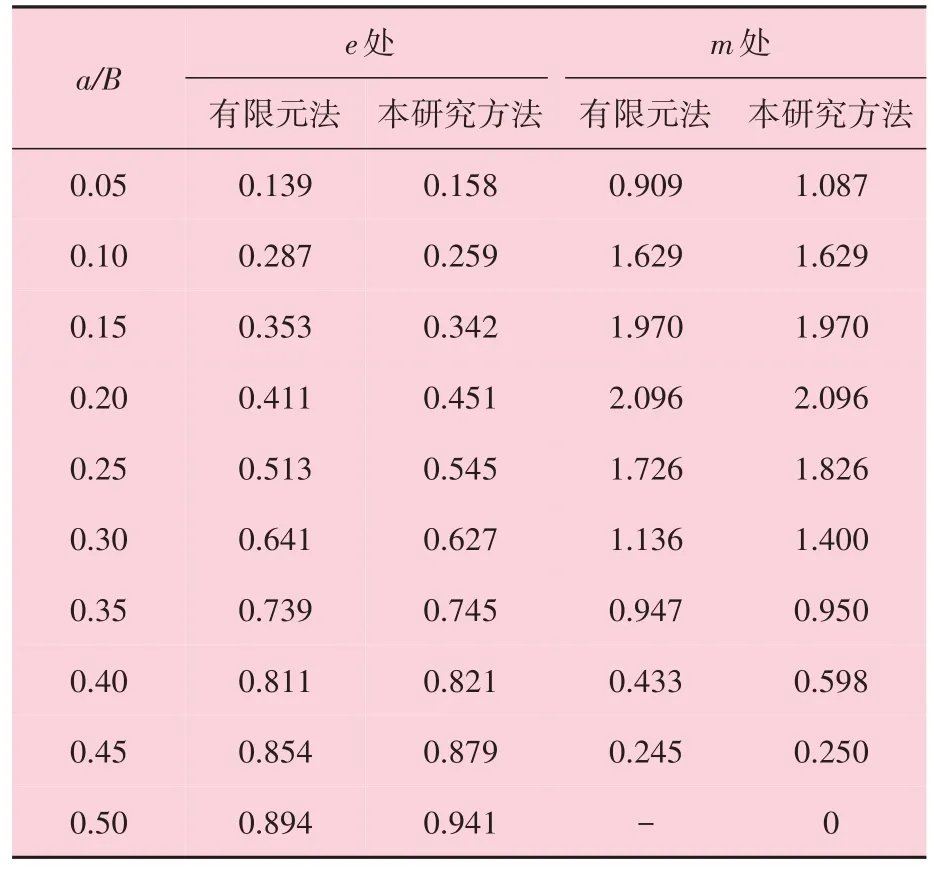
表1 裂紋尖端e、m處應力強度因子有限元解與本研究解的比較

圖4 含R槽方形殼的有限元網格

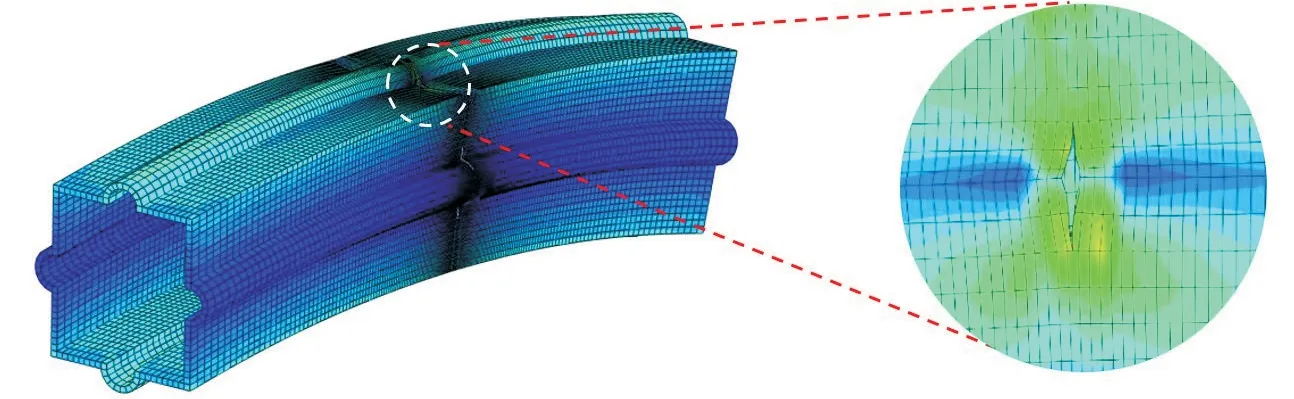
圖5 含R槽方形殼的有限元模型應力云圖

5.1 彎曲作用下含R槽方形殼對稱穿透角裂紋的應力強度因子有限元解與本研究解的比較

在本研究有限元解與模型計算解對比過程中，共提取10組有限元數據正則化裂紋長度a/B=0.05、0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45 和0.5。當a/B=0.5 時裂紋尖端e點應力強度因子fe（a/B）的本研究解為0.941，有限元解為0.894，相對誤差為4.99%，驗證了模型計算方法的準確性。

彎曲作用下含R 槽方形殼對稱穿透角裂紋的正則化應力強度因子有限元解與本研究解的比較如圖6 所示。從圖6 可以看出，在含R 槽方形殼對稱穿透角裂紋尖端e點，應力強度因子隨著裂紋面的擴展呈現非線性增大趨勢；在裂紋尖端m點，應力強度因子隨著裂紋面的擴展先增大后減小，在a/B=0.2 處取得最大值。

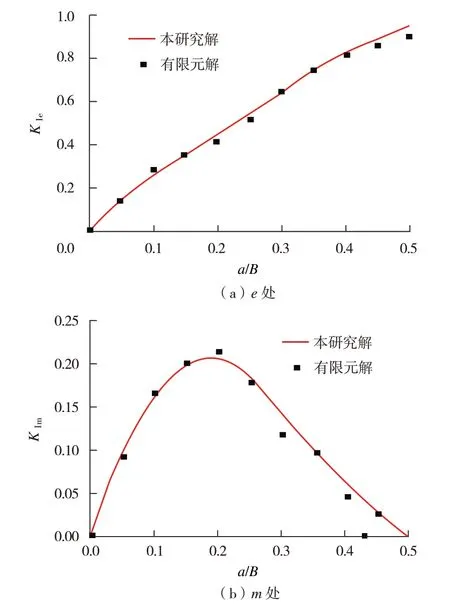
圖6 彎曲載荷作用下對稱穿透角裂紋正則化應力強度因子

5.2 拉伸和彎曲載荷作用下含R槽方形殼對稱穿透角裂紋的應力強度因子解與有限元解的比較

選取a/B=0.1 時，拉伸和彎曲載荷作用下含R 槽方形殼的角裂紋尖端m處（公式（31））和e處正則化應力強度因子計算結果，與有限元分析結果進行對比，對比結果如圖7所示，通過圖7 可以看出，兩種方法所得結果基本吻合，并在a/B=0.45 時取得最大值，最大誤差為12.8%，滿足工程實際要求。

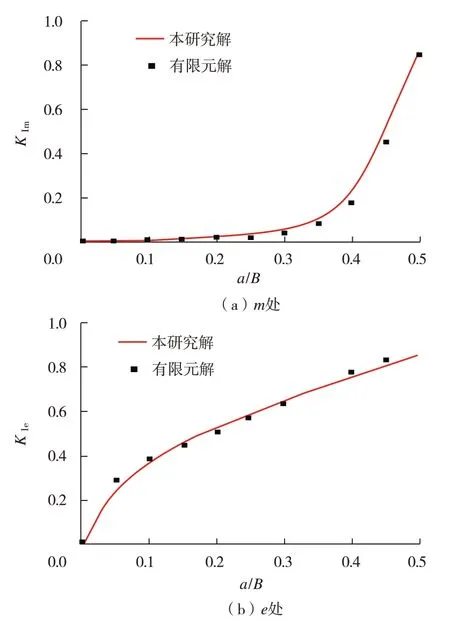
圖7 拉伸和彎曲載荷作用下裂紋尖端正則化應力強度因子

6 結 論

（1）基于J2積分、G積分和材料力學中截面應力分析理論，構建了在一定拉伸和彎曲載荷共同作用下，裂紋截面不同奇異應力場對應的應力強度因子求解方法。

（2）證明了J2積分以及材料力學中平截面假定對于估算拉伸和彎曲載荷作用下裂紋尖端具有多個應力場的不同應力強度因子是可行的。

（3）基于基本力學和σ=My/I，可以找到不同應力強度因子之間的簡單關系，為解決不同應力場所對應的應力強度因子問題提供了思路。

（4）簡化了具有對稱穿透裂紋的工程構件的應力強度因子求解，并且所有分析和計算都在基本力學范圍內，且誤差在實際工程可接受范圍之內。

（5）推導了含R槽方形殼對稱穿透角裂紋在拉伸和彎曲載荷共同作用下的一系列閉合形式的應力強度因子表達式，為類似工程構件的應力強度因子求解提供參考。