基于CFD方法的高線速度齒輪最優噴嘴布置角度設計*

夏建芳 姚 恒 陳思雨 王志偉 陶 軒 胡小舟

(中南大學機電工程學院 湖南長沙 410083)

在高速齒輪傳動系統中，通常使用噴油潤滑的方式對傳動系統進行潤滑與冷卻。然而隨著齒輪轉速升高，齒輪旋轉所產生的氣流會形成空氣屏障，阻礙潤滑油進入齒輪嚙合點且使潤滑油流束破碎[1]，導致嚙合區的潤滑油量減少，進而導致潤滑效率降低。AKIN等[2-5]針對不同齒輪的不同嚙合狀態、噴油方向的噴油潤滑進行了一系列的研究，發現潤滑效率不僅與噴油參數和傳動比參數有關，還受噴油位置和角度的影響。

如何對噴油潤滑系統的相關參數進行設計以最大限度地提升潤滑效率，減少系統使用的油量，同時保持齒輪箱的可靠性，了解齒輪箱內部的潤滑油流場的動態特性是非常有必要的。目前普遍采用計算機仿真模擬的方法研究復雜箱體內流體的流動情況[6]。

2009年，ARISAWA等[7]首次采用油/空氣兩相流CFD(Computational Fluid Dynamics)方法對齒輪風阻與攪油損失進行研究，并證明該方法是研究高速齒輪風阻損失的有效工具。FONDELLI等[8]在2015年運用CFD方法模擬了齒輪噴油潤滑過程，并評估了噴油潤滑所產生的阻力扭矩。曹寓等人[9]在2017年在 FLUENT中采用 VOF模型及動網格技術進行流場動態仿真，得出了不同時刻齒輪箱內各個位置油液的體積分數以及油壓、流速的變化規律，分析了不同噴油流量對齒輪潤滑效果的影響。NIU、WANG等[10-14]先后利用CFX與Fluent軟件建立了流體動力分析模型，研究了超高速齒輪噴油潤滑時，各工況參數對油流束方向偏離乃至對潤滑效率的影響，并給出了克服齒輪旋轉引起空氣屏障對潤滑阻礙作用的方法。DAI 、CHEN等[15-17]先后通過商用CFD軟件研究了噴嘴入射角度、噴嘴與嚙合點距離等布置參數對潤滑效率的影響，比較得出最優噴嘴布置方案。

目前，對于高速齒輪箱的潤滑問題，主要是運用商用流體軟件對齒輪箱內部的流體動態特性分析，以進一步優化噴油潤滑系統的設計，但總的來說，開展的時間較晚，相關報道較少。雖然上述文獻對噴嘴布置方式進行了相關研究，但多數是依靠經驗設計試驗方案，通過仿真分析比較各方案得出最優方案，這樣不僅會花費大量的時間在仿真計算上，而且得到的只是設計方案的最優方案，并不是理論上的最優方案。

本文作者針對高線速度齒輪的噴油潤滑問題，通過流體軟件仿真研究了齒輪箱中流場的動態特性，對噴油潤滑中齒輪旋轉產生的氣流與噴油流束的干涉問題進行分析，利用流場流線圖尋找最優噴嘴布置角度，并研究噴嘴角度布置與齒輪傳動比和轉速的影響。

1 噴油潤滑理論分析

1.1 湍流模型

齒輪噴油潤滑過程中，流體為有旋流動，且流體在齒輪彎曲壁面上流動，流體有較大的應變率，故選擇RNGk-ε湍流模型[18-19]。湍流動能k和湍流動能耗散率ε方程為

(1)

(2)

其中，

(3)

式中：ρ為流體密度；x和t分別為位移和時間分量；i、j為張量指標；μt是湍流黏性系數；μ是混合流體湍流黏性系數；R為凈相變率；Gk是由平均速度梯度產生的湍流動能；Gb是由浮力影響產生的湍流動能；YM為可壓縮湍流脈動膨脹對總的耗散率的影響；αk、αε分別為湍流動能和耗散率的有效普朗特數的倒數；Cμ、C1ε、C2ε、C3ε為模型常數，由Fluent軟件給出。

1.2 VOF模型

VOF(Volume of Fluid)多相流模型是一種求解多相流動和自由表面流動的計算模型，引入各項流體體積分數來跟蹤2個或多個不混溶流體區域的自由表面[20]。對于文中的潤滑油-空氣兩相流系統，該方法分別求解流體運動的動量方程和計算域內相分布的體積分數方程，由于僅由潤滑油或空氣占據的控制體積域分別具有0或1的體積分數，故2種不混溶的流體(潤滑油-空氣)之間的界面位置可以根據計算域內的體積分數分布來確定，每個控制體積域內的流體物理參數是在平均流體體積分數的基礎上計算的[21]：

(4)

式中：φ代表流體的物理參數；α代表體積分數，且α1+α2=1。

2 齒輪箱內部噴油潤滑流場計算模型

2.1 幾何模型

文中采用直齒輪嚙入側噴油進行研究，表1給出了其幾何模型和基本工況參數。為避免嚙合區網格之間尺寸相差過大導致網格畸變進而導致計算出錯，將齒輪對的中心距擴大1 mm。

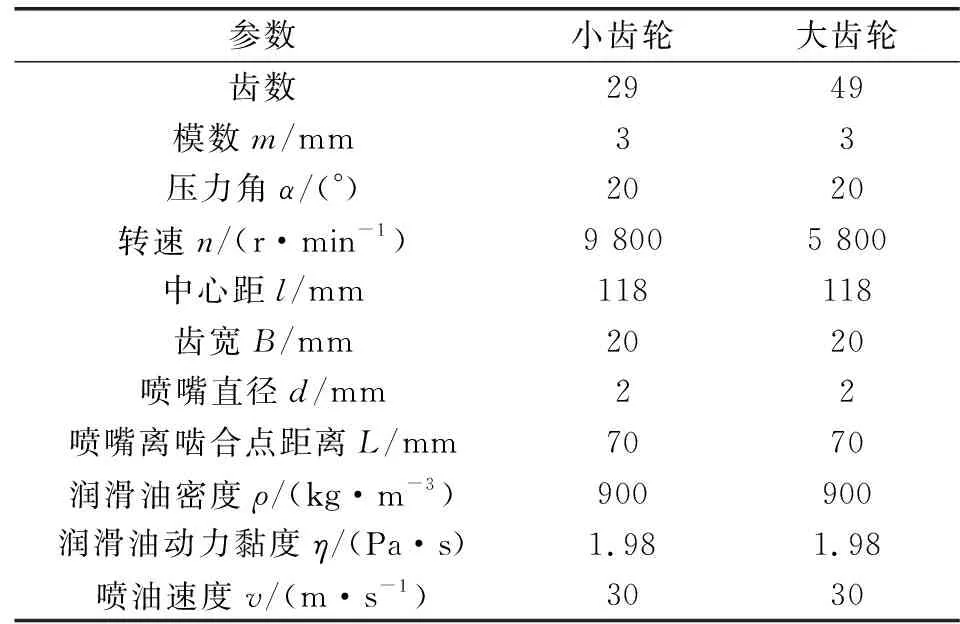
表1 齒輪箱幾何參數和工況參數Table 1 Gometric parameters and working condition parameters of gearbox

2.2 流場計算模型

將齒輪對導入Ansys Spaceclaim中，抽取流體外殼作為齒輪箱內部流體域。為了提高仿真準確性以及清晰地表征噴油流束的流動情況，需要將噴油流束流經的路徑進行網格加密。故將潤滑油流束流過的路徑取一圓柱(如圖1(a)所示)，再與原流體域進行布爾運算相減，形成中間與外部2個部分的流體域，并采用共享拓撲的方式，使2個流體域共用邊界面。目的是使2個流體域網格共節點，在仿真過程中的網格重構中更加流暢，并減少結構中的邊界面數量。在Ansys Meshing模塊中，將外部流體域采用默認的網格劃分方式，識別曲率與臨近度，將內部流體域的網格加密到0.5 mm，最終網格數為2 766 997(如圖1(b)所示)，并導入到Fluent模塊。

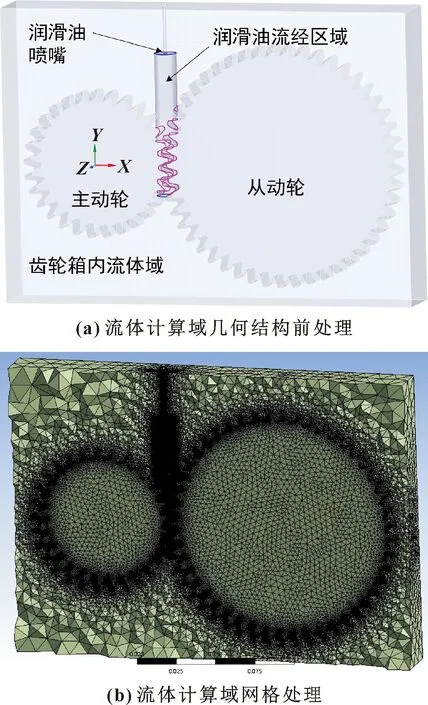
圖1 流體計算域幾何結構與網格處理示意Fig.1 Schematic fluid domain geometry and mesh processing： (a)geometry；(b)mesh

Fluent軟件仿真的主要設置如下：時間選項為瞬態，采用VOF多相流模型，打開隱式選項，湍流模型選擇RNGk-ε模型，臨近壁面選擇標準壁面函數，材料中引入潤滑油與空氣分別作為多相流中的兩項，噴嘴出口為速度入口，水力直徑為2 mm。底部作為壓力出口，所有墻面都是用非滑動靜止壁面條件。求解器中，壓力速度耦合采用標準SIMPLE算法，梯度差分選項中選擇最小二乘方法，壓力選項中選擇PRESTO！，湍流動能選項中選擇二階迎風格式。

Some relations between prime inner operators,prime closure operators and connections

齒輪轉動采用動網格技術進行模擬，采用鋪層法與局部重構法對網格進行控制，選擇齒輪對為動網格控制區域，選擇區域類型為剛體。運算時間步長為1×10-6s。

3 最優噴嘴角度的提取方法與驗證

3.1 最優噴嘴角度的提取

圖2所示是潤滑油體積分數渲染圖，為了顯示嚙合區的潤滑油分布，將小齒輪透明化顯示。圖片中表明潤滑油能夠順利進入嚙合區進行潤滑與冷卻，圖3(a)所示是齒輪箱內速度矢量分布，速度矢量能夠表示齒輪箱內各點上的速度方向與大小，流場整體的速度矢量分布能夠區域性地表示齒輪箱內的空氣流動狀況。圖3(b)所示是齒輪箱底部視角的速度矢量分布，可以看出齒輪在嚙合處有部分的軸向流動，且在齒輪邊緣速度矢量會集中在齒輪的齒寬中心。

圖2 潤滑油體積分數渲染Fig.2 Rendering of oil volume fraction

圖4所示為齒輪中間截面上的速度流線，速度流線是與流場中每一點上的速度矢量相切的曲線，代表了流場中各點的流動路徑，區別于速度矢量圖，流線圖更強調質點運動的連續性。圖4(a)所示是正常工況下截面上的流場流線，齒輪高速旋轉在齒頂周圍形成了空氣屏障，噴油流束突破了空氣屏障進入到齒輪嚙合區進行潤滑；在噴油過程中，空氣屏障與噴油流束發生干涉，導致流入嚙合區的油量減少，流體動力損失增大，潤滑效率降低；同時，噴油流束也影響了齒輪周圍的空氣流動狀況。

因此，為了研究齒輪原始工作情況下周圍的空氣流動狀況，調出停止噴油齒輪空轉時的速度流線圖(如圖4(b)所示)，發現除了在嚙合區上方之外，其他區域的空氣流動都與圖4(a)相似。將圖4(b)中方框部分的嚙合區上方流線放大(如圖5所示)，可以看出，齒輪對旋轉分別產生的空氣屏障在嚙合區上方發生干涉并結合成一條進入嚙合區的路徑，該路徑將引導氣流進入嚙合區。如果將潤滑油沿該方向射入，會最大程度地減少空氣屏障干涉所引起的潤滑油流失和噴油流束破裂，并減少流體動力損失，點B為氣流首次沖擊齒面的接觸點。

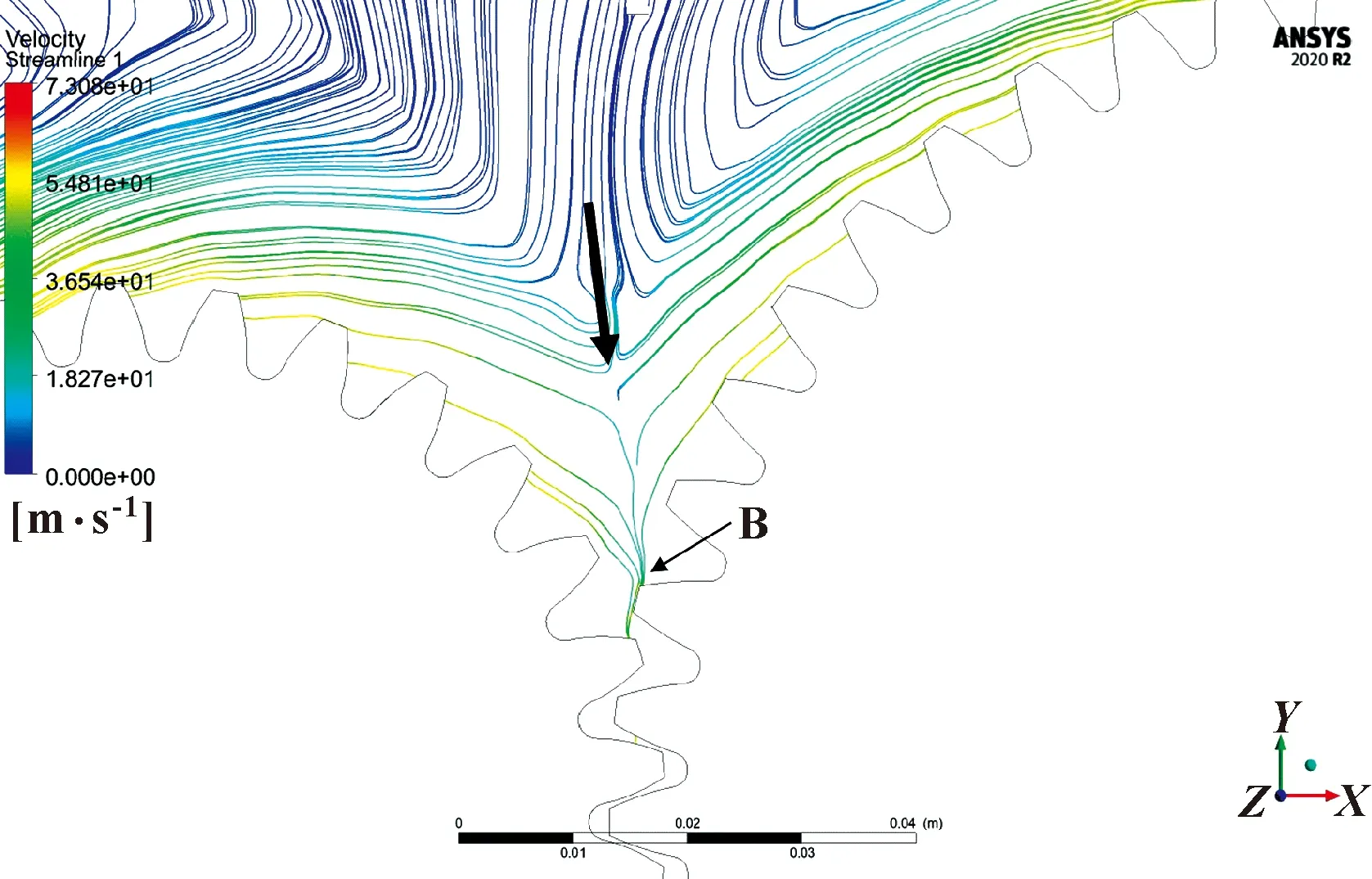
圖5 齒輪空轉時嚙合區上方的流線放大圖Fig.5 Enlarged view of flow field streamline in meshing area without oil injection

提取出圖5中的理想角度，如圖6(a)所示。R(Ra)、r(ra)分別為大齒輪與小齒輪的分度圓半徑(齒頂圓半徑)，點A為噴嘴出口，點B為氣流與齒面的接觸點，也是氣流進入嚙合區的入射點。AB連線與垂直方向上的夾角即理想噴嘴角度為7.37°，流線中提取出的理想角度路徑并不通過分度圓相切點C，這是因為氣流首先沖擊齒面，隨后由齒面旋轉帶動到嚙合點，同時流線失去連續性。

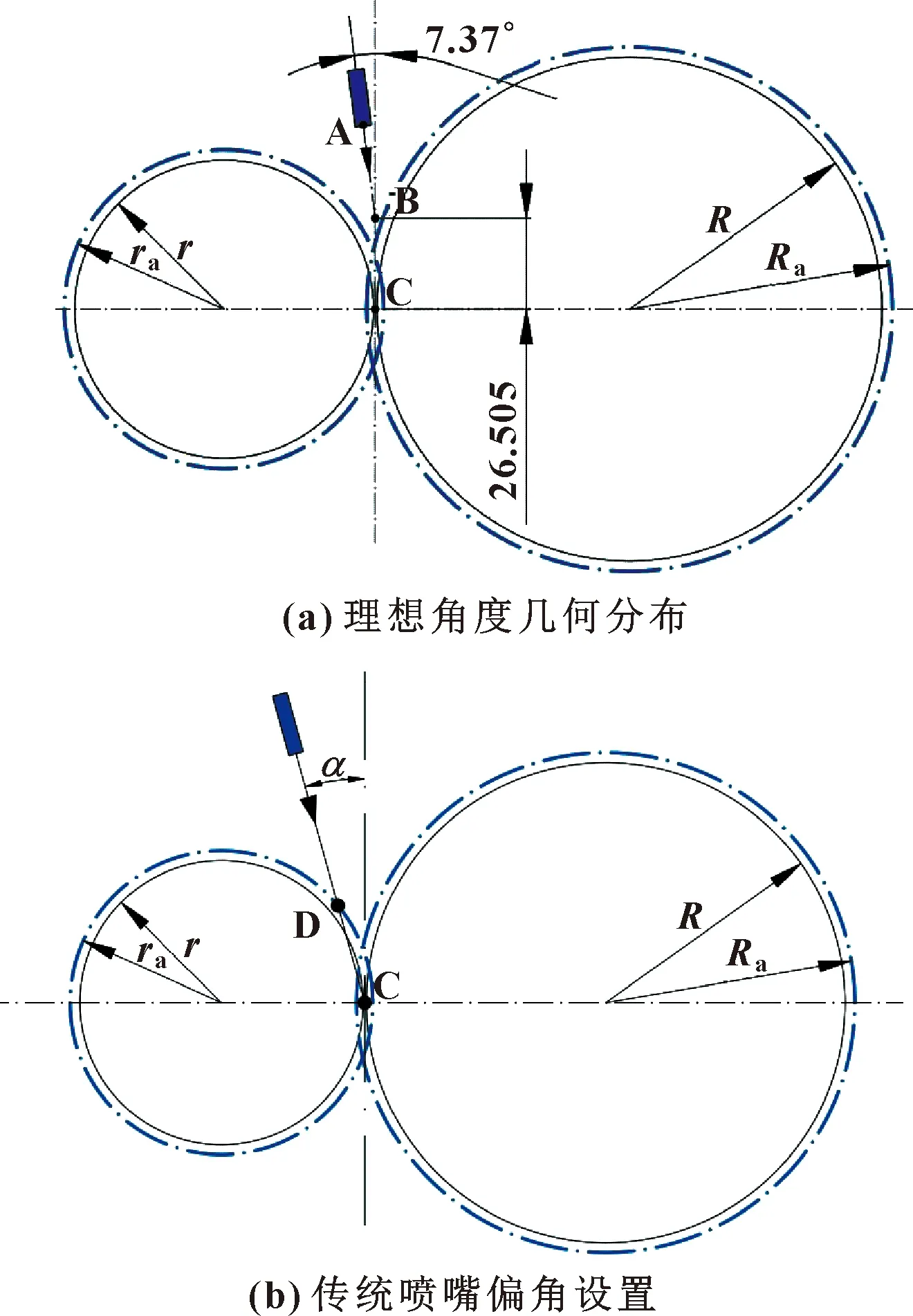
圖6 噴嘴角度設置示意Fig.6 Schematic of nozzle angle：(a)geometric distribution of the measured optimal angle；(b)traditional nozzle deflection setting

圖6(b)所示是目前傳統的噴嘴角度設置[14-15]，噴射流方向指向點C，偏角α為噴嘴出口與點C連線與垂直方向的夾角。當噴嘴按照該設置方式布置時，噴油流束將在點D沖擊未嚙合齒面，導致油流束破碎乃至進入嚙合區的油量減少以及噴油流束的沖擊動量降低，從而潤滑效率降低。

3.2 最優噴嘴角度的潤滑效率驗證

如圖7所示，為了驗證提取出的理想角度是否擁有最高的潤滑效率，分別設置圖6(b)中α角為5°、0°、-5°，以及圖6(a)中理想角度，進行了仿真模擬。

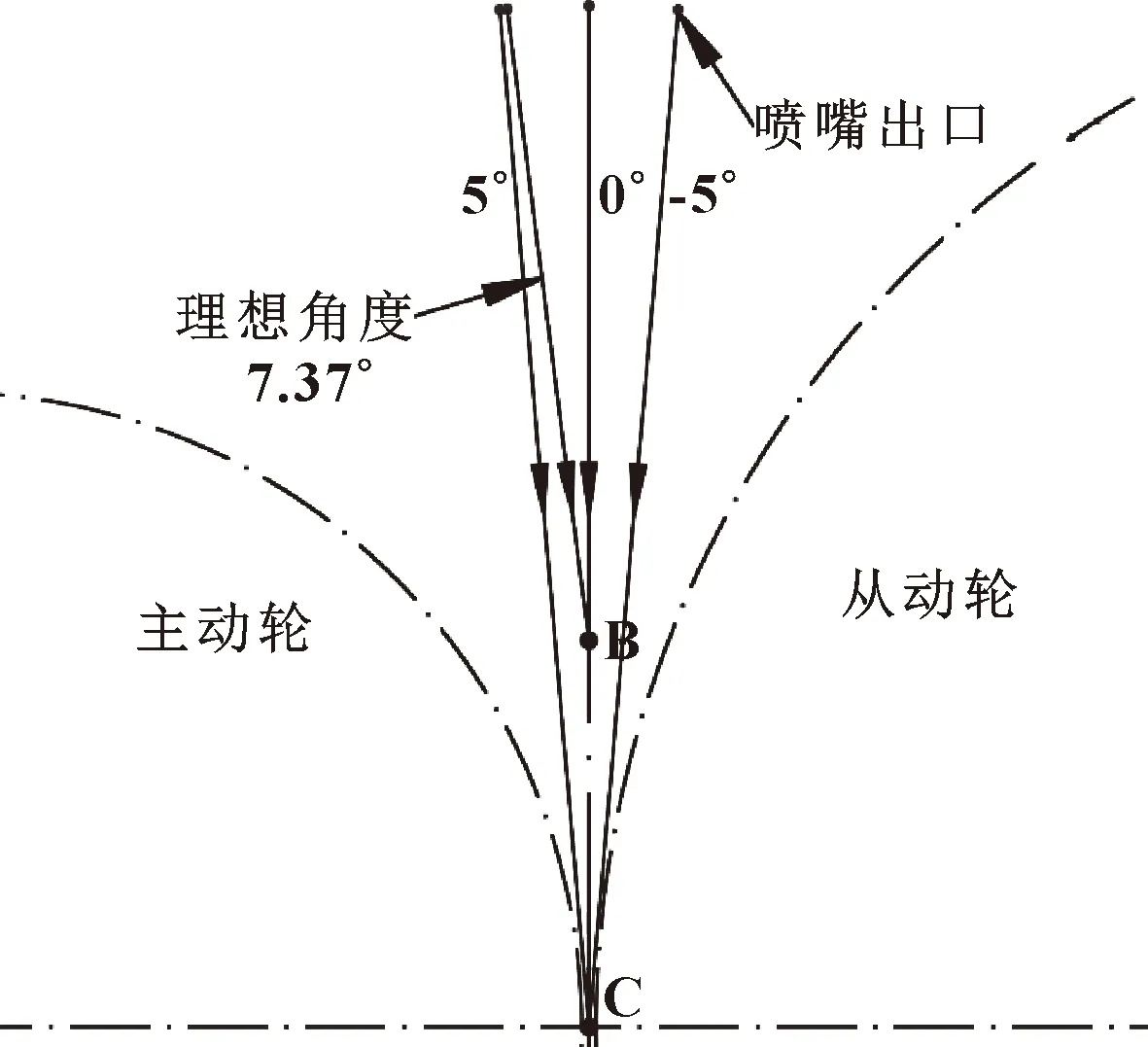
圖7 4組噴嘴角度設置Fig.7 Four sets of nozzle angle settings

圖8所示是分別在4組噴嘴角度設置下小齒輪上的潤滑油體積分數云圖。可以看出，按照理想角度設置的組別齒輪嚙合區潤滑油體積分數更大，潤滑油油量更大，分布更集中于嚙合中心區。噴嘴角度為5°時的潤滑油分布較分散，這是因為偏轉的角度過大，潤滑油首先噴到小齒輪還未嚙合的齒面上，導致嚙合區的體積分數較少。直齒輪傳動的重合度一般不大于2，工作中嚙合狀態的齒面數不超過2，所以潤滑油需要集中在嚙合狀態的1到2個齒面上。噴嘴角度為0°和-5°時潤滑油分布比5°時稍好，但仍較分散，且嚙合齒面上的潤滑油體積分數不高。按照理想噴嘴角度布置時，潤滑油集中在嚙合區的少數齒，證明潤滑油的沖擊深度很深，潤滑效果在幾組中最好。

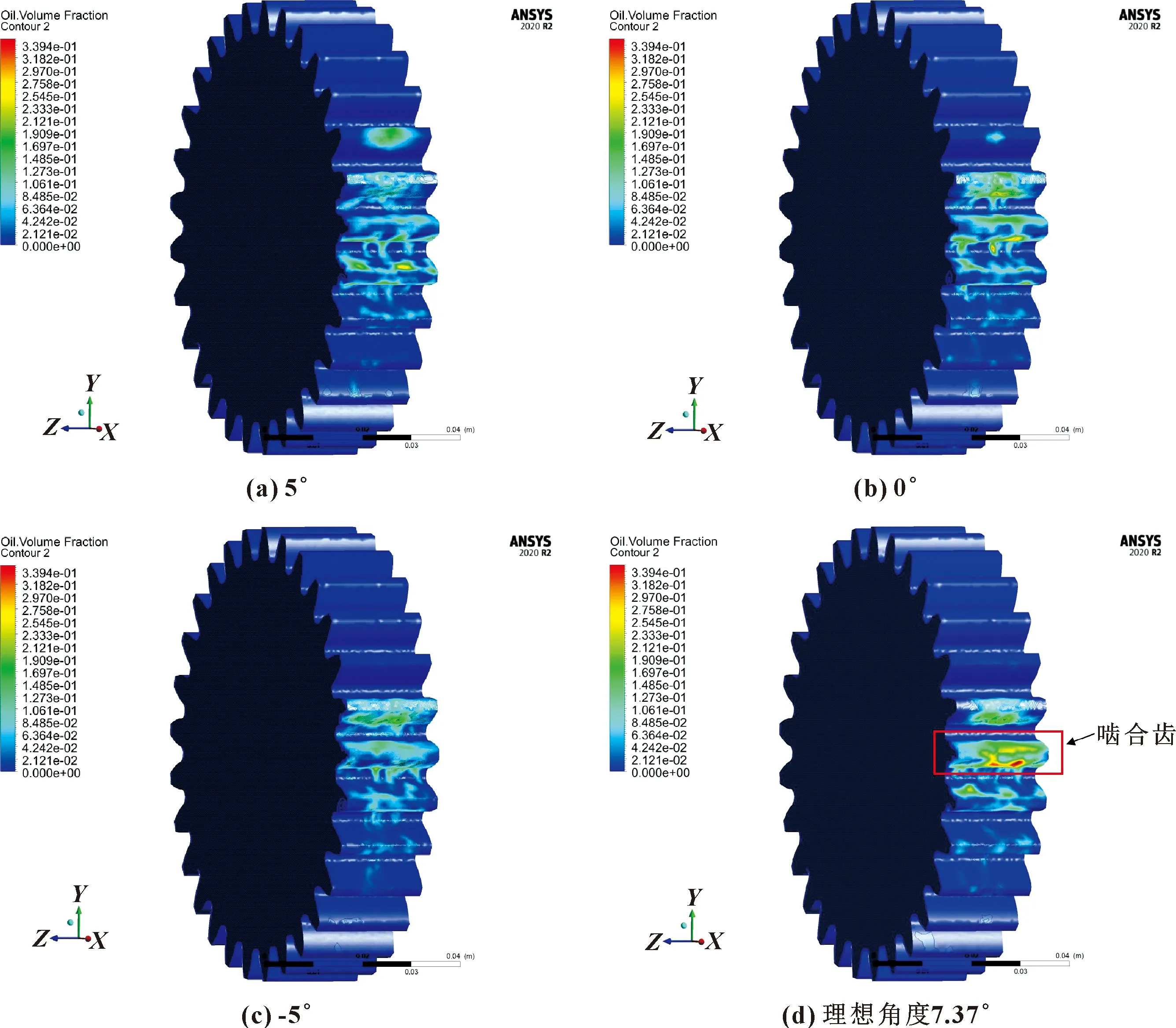
圖8 4組噴嘴角度設置的潤滑油在小齒輪上的體積分數分布云圖Fig.8 Contour of volume fraction distribution of lubricating oil on pinion of four sets of nozzle angle settings： (a)5°；(b)0°；(c)-5°；(d)optimal angle 7.37°

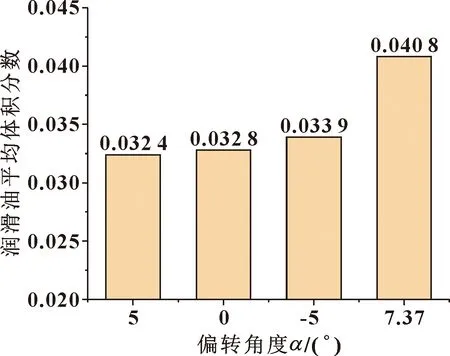
圖9 4組噴嘴角度設置的潤滑油平均體積分數Fig.9 Average volume fraction of lubricating oil of four sets of nozzle angle settings

文獻[17]中表明，嚙合區附近油壓可視為判斷齒輪潤滑性能的標準。圖10所示是小齒輪上的油壓分布。可以看出，噴嘴按照理想角度7.37°設置時，嚙合區擁有最大負壓(絕對值)，即吸入潤滑油的能力最強，另外3組在嚙合區的負壓大小與分布狀況相似，但在小齒輪進入嚙合區前的齒面上出現了正壓峰值區域，這是潤滑油流束噴至齒輪時產生的接觸壓力。α=5°時，嚙合區前齒面壓力峰值區域最大，且峰值最高；α=-5°時，峰值區域最小，峰值最小。這是因為α=5°時噴嘴向小齒輪偏轉的角度過大，潤滑油流束先沖擊了小齒輪上的未嚙合齒，并沒有順利進入嚙合區。而α=-5°時，噴嘴向大齒輪偏轉，先沖擊大齒輪上的未嚙合齒，故小齒輪上沒有壓力峰值區域。

圖10 4組噴嘴角度設置時小齒輪上油壓分布Fig.10 Oil pressure distribution on pinion of four sets of nozzle angle settings：(a)5°；(b)0°；(c)-5°；(d)optimal angle 7.37°

同時輸出嚙合區球體內的平均正壓、平均負壓、平均壓力，如圖11所示。在齒輪旋轉時，旋轉產生的氣流在嚙合處產生負壓，形成卷吸效應，將潤滑油吸入嚙合區進行潤滑，所以嚙合區負壓是促進潤滑油吸入嚙合區的主要因素。從圖11可以看出，噴嘴按照理想角度7.37°設置時，嚙合區平均負壓、平均壓力(負值)的絕對值最大，平均正壓最小，吸入潤滑油的能力最強因而潤滑效率最高，驗證了當噴嘴按照由流線提取出的理想噴嘴角度布置時擁有最高的潤滑效率。

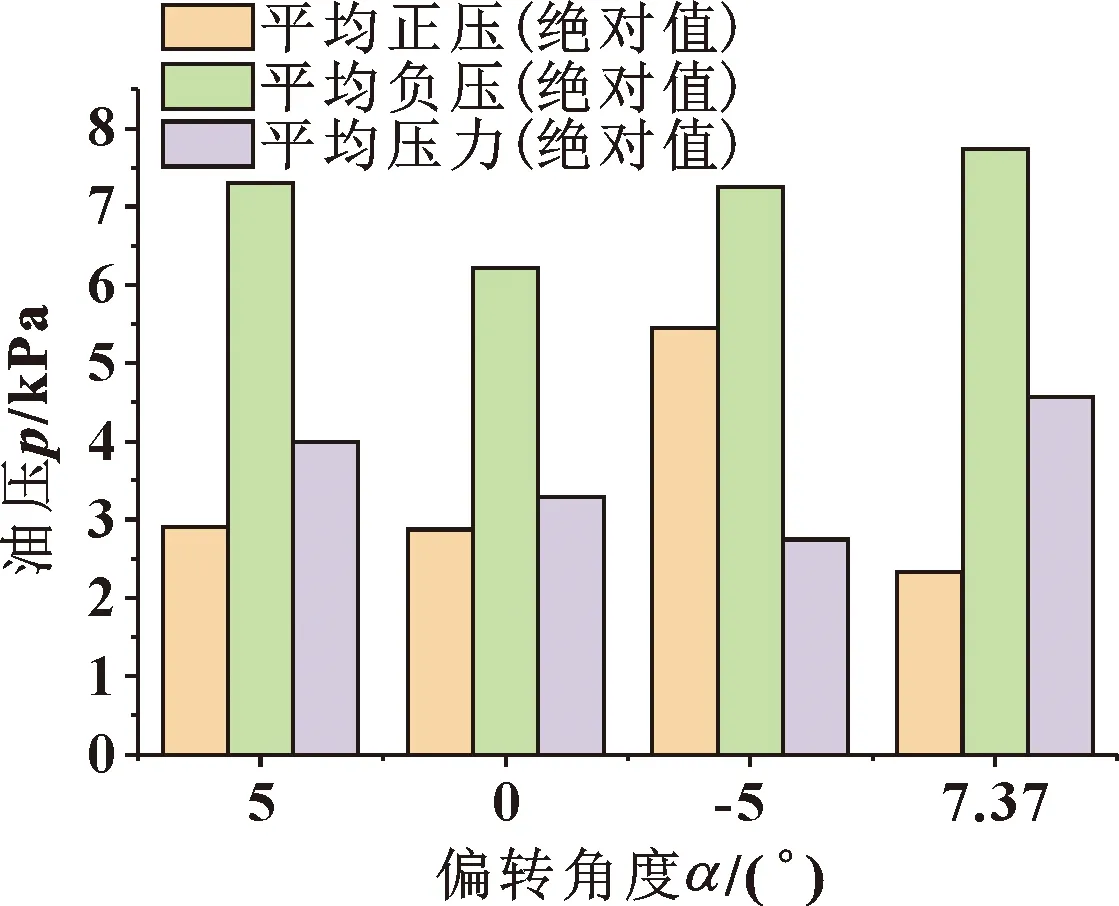
圖11 4組噴嘴角度設置時的油壓統計數據Fig.11 Oil pressure statistics of four sets of nozzle angle settings

4 不同工況參數對噴嘴角度設置的影響

為了研究齒輪幾何特征和各工況參數對噴嘴角度設置的影響進而分析齒輪箱內的空氣流動規律，設置不同的齒輪傳動比與轉速進行了仿真分析對比。

4.1 傳動比對噴嘴角度設置的影響

傳動比影響著齒輪的幾何尺寸，文中保持小齒輪齒數不變，大齒輪齒數變化(按表2中設置)進行仿真，不設置噴油、不加載荷，使齒輪空轉，小齒輪轉速保持為9 800 r/min，其他設置不變，提取出齒輪中間截面的嚙合區速度流線圖，如圖12所示。

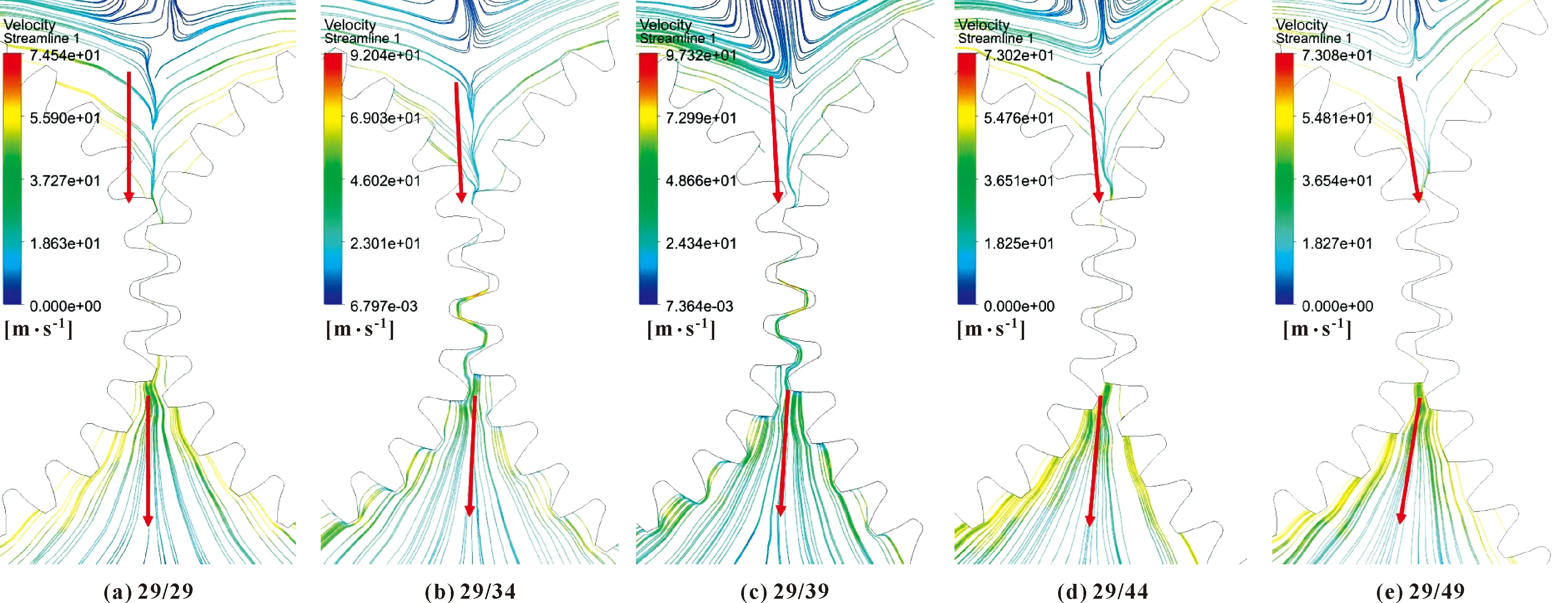
圖12 不同齒數比下嚙合區流線Fig.12 Streamline of meshing area under different tooth ratio：(a)29/29；(b)29/34；(c)29/39；(d)29/44；(e)29/49

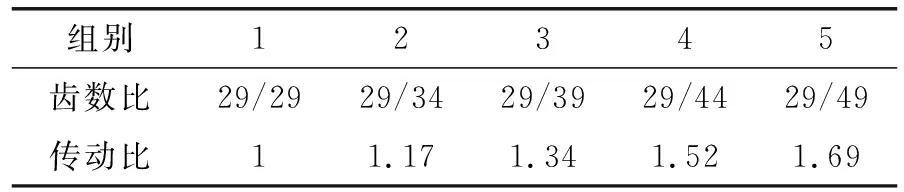
表2 不同組別轉動比的設置Table 2 Gear ratio settings of different groups

如圖12中的箭頭所示，當傳動比為1(29/29)時，嚙合區上方的流線垂直向下進入嚙合區，嚙合區下方的流線同樣也是垂直向下流出。當傳動比增大時，上方流進嚙合區的流線路徑以及下方流出嚙合區的流線路徑均逐漸向小齒輪偏轉，且流入流出路徑沿齒輪中心距連線對稱。將圖中路徑角度提取出來并擬合(見圖13)，發現當傳動比從1(29/29)逐漸增大到1.69(49/29)，進入嚙合區的流線路徑逐漸向小齒輪偏轉，與垂直方向夾角從0°增大到7.37°，且偏轉角度與傳動比呈正相關，擬合后的一次函數方程為

圖13 傳動比與擬合區上方流線偏轉角度的關系Fig.13 Relationship between gear ratio and streamline deflection angle above fitting area：(a)streamline angle above the meshing area of 5 groups of different gear ratios：(b)relationship and fitting curve between deflection angle and gear ratio

y=9.761x-9.177

(5)

已經驗證進入嚙合區的流線路徑即為最優噴嘴布置角度，所以以上結論同時說明，當傳動比增大時，最優噴嘴布置角度也同樣向小齒輪偏轉，且與傳動比呈正相關。在傳動比為1時，最優噴嘴角度為垂直向下噴油。

4.2 轉速對噴嘴角度設置的影響

齒輪幾何特征改變時，流場中的流動狀況發生變化。為了研究在幾何特征不變時流場中流動情況是否會因為其他工況參數的變化而變化，還需要對不同轉速的傳動組合進行研究。文中在齒數比為29/49保持不變，小齒輪轉速分別設置為1 450、2 900、4 350、5 800 r/min進行仿真，分別調出嚙合區的流場流線，如圖14所示。

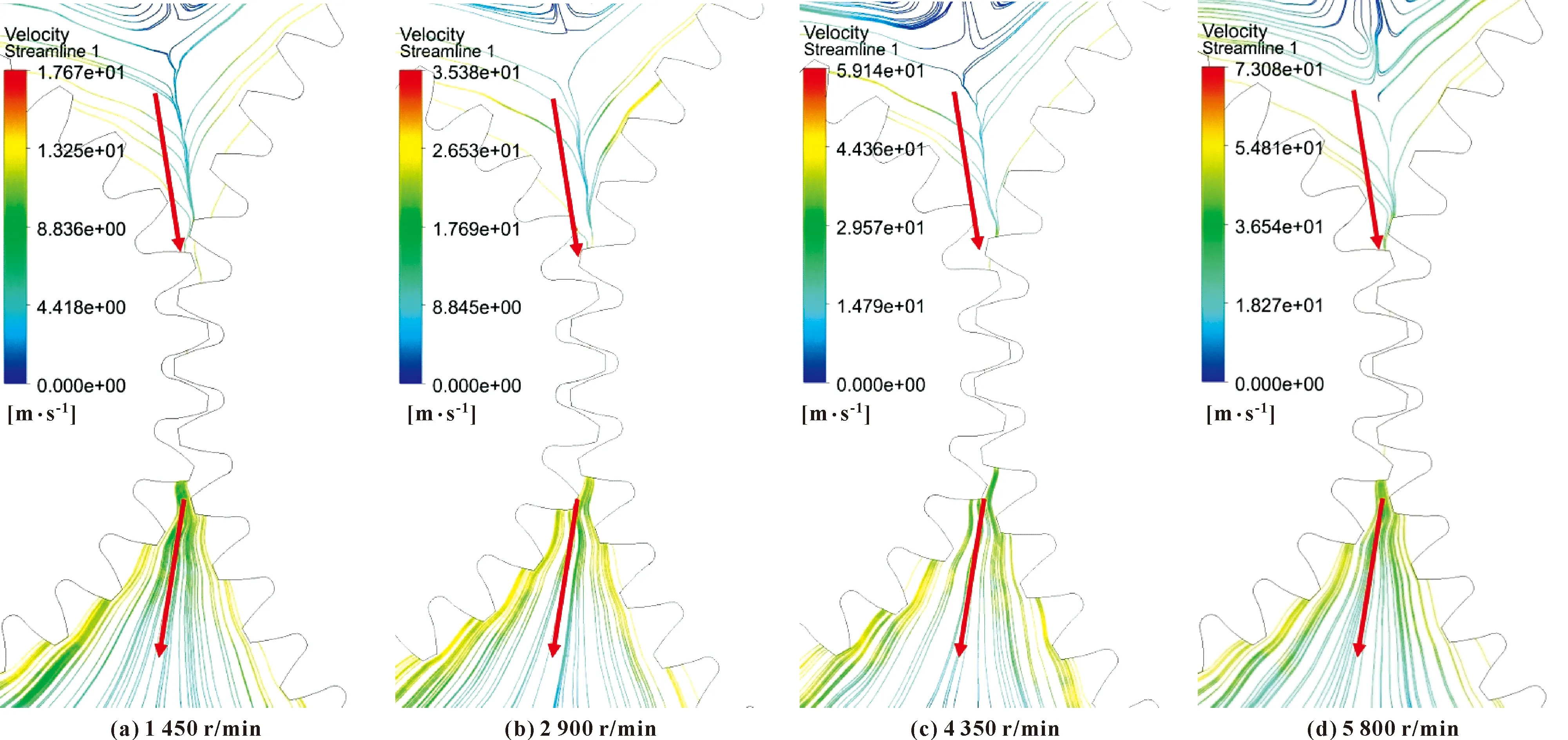
圖14 不同轉速下嚙合區流線Fig.14 Streamline of meshing area at different speeds：(a)1 450 r/min；(b)2 900 r/min；(c)4 350 r/min；(d)5 800 r/min

如圖14所示，齒輪轉速變化時，齒輪箱內的流線分布變化不大，即空氣流動的分布變化不大。從紅色箭頭看，進入嚙合區的路徑偏轉角度幾乎不變，且流出路徑與流入路徑沿中心距連線對稱。

圖15所示是嚙合區上方流線偏轉角度與轉速的關系。隨著轉速增大，嚙合區上方的跡線偏轉角度變化不大，最大偏轉角度在轉速為2 900 r/min時為7.89°，最小偏轉角度在轉速為5 800 r/min時為7.37°，差距小于7%。這說明在齒輪噴油潤滑系統中，當轉速設置變化時，不需要重新調整噴嘴角度。

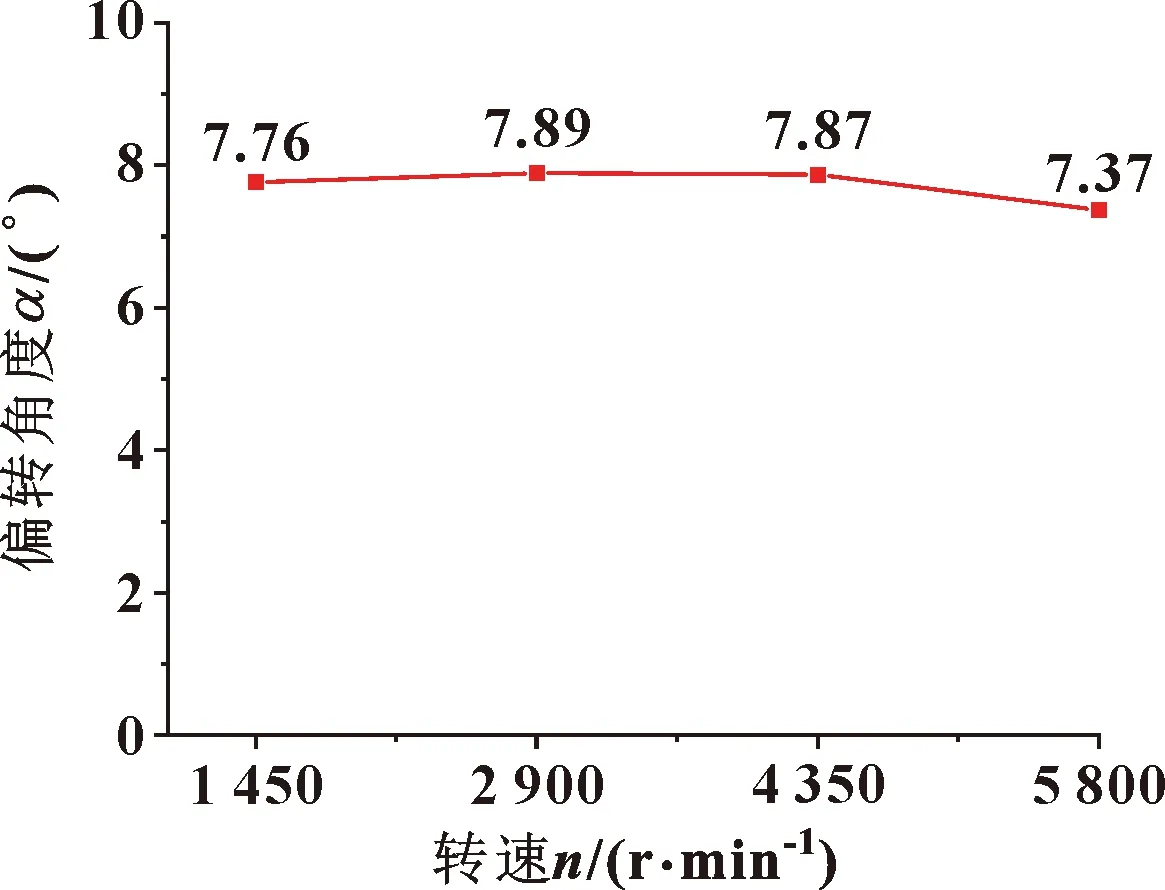
圖15 嚙合區上方流線偏轉角度與轉速的關系Fig.15 Relationship between streamline deflection angle and rotational speed above meshing area

從目前的仿真結果來看，轉速的大小只與嚙合區附近空氣的流動速度有關，與分布狀況與流動方向無關，故不影響最優噴嘴角度的設置，這也說明最優噴嘴角度只與齒輪幾何結構有關，與工況參數設置無關。WANG等[11]研究認為，齒輪轉速增大會影響噴油流束的正常流動，導致偏轉。這是因為齒輪周圍旋轉形成的氣流的速度增大會破壞潤滑油流束維持原有圓柱狀流束的能力，與此同時，齒輪空轉時周圍的氣流分布與流動方向并沒有發生改變。

5 結論

(1)高線速度齒輪嚙合區域有部分軸向流動，且在齒輪邊緣速度矢量會集中在齒輪的齒寬中心。

(2)齒輪嚙合區域存在負壓區域，會使潤滑油吸入嚙合區(卷吸效應)，通過流場流線圖發現嚙合區域上方跡線重合，形成一條進入嚙合區域的氣流。將噴油嘴按照該氣流角度設置，仿真計算發現，在該噴嘴角度設置下，齒輪嚙合區擁有最大的潤滑油體積分數及油壓，以及最高的潤滑效率，證明了最優噴嘴角度的存在。

(3)齒輪傳動比增大，嚙合區上方氣流(最優噴嘴角度)向小齒輪偏轉。齒輪轉速增大時，氣流流動速度增大，但氣流的分布狀況和流動方向不受影響，說明齒輪周圍氣流流動狀況和最優噴嘴角度只與齒輪幾何結構有關，與工況參數設置無關，且最優噴嘴角度與傳動比呈正相關。