基于Inventor有限元仿真的異步電機轉子模態分析

俞林,范利輝,孫明昌

(隔而固(青島)振動控制有限公司,山東青島 266108)

0 引言

三相異步電機具有結構簡單、運行可靠、重量輕和價格便宜等優點而廣泛應用于機械設備、家用電器、冶金與礦山機械等領域[1]。轉子機構是異步電機的重要核電部件之一,由于加工精度等因素,在電機轉子高速轉動時不可避免的會產生離心力,而導致產生電機轉子機構的振動,轉子機構振動會使軸承及電機其他結構出現疲勞破壞,進而直接影響電機的使用壽命。因此,分析電機轉子機構的模態特性,對減小電機振動,提高電機壽命有重要意義。電機模態分析方法主要有解析法、試驗法和有限元法,其中,解析法是最早應用于電機模態分析方法,其優點在于概念清晰,易于定性,缺點是僅對簡單結構模型適用,對復雜模型很難獲得高精度結果;試驗法可以獲得比較準備的模態參數,但由于需要大量傳感器和測試設備,試驗周期比較長,成本也比較高。有限元法具有對復雜結構模態分析精度高,計算周期短,成本低等優點,隨著有限元計算技術發展和有限元軟件的逐漸完善,有限元法在電機模態計算領域得到廣泛應用。席榮盛等應用有限元法計算出了電動汽車永磁同步電機固有頻率。王超應用有限元法精確計算柴油發電機組軸系的各階固有頻率和模態分析。

本文基于模態分析理論,通過Inventor仿真軟件對三相異步電機轉子機構進行模態分析,計算出轉子機構前八階固有頻率及模態特性,為轉子機構結構優化和產品迭代提供設計依據。

1 模態分析基本理論

模態是機械結構的固有振動特征,每一個模態具有特定的固有頻率、阻尼比和模態振型。模態分析是將線性定常系統振動微分方程組中的物理坐標變換為模態坐標,使方程組解耦,成為一組以模態坐標及模態參數描述的獨立方程,以便求出系統的模態參數[2、3]。

根據動力學理論,系統的振動遵循如下微分方程

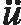
(1)

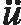
模態分析基于系統的無阻尼自由振動,即上式可以表示為

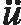
(2)

設想系統產生同頻率、同相位但各質點不同振幅的振動

u(t)=φsin(ωt+θ)

(3)

由式(2)、式(3)得這一運動需滿足的條件是存在非零向量φ得

([K]-ω2[M])φ=0

(4)

滿足式(4)的特征根ωr即為系統模態的固有頻率,非零解向量φr即為對應頻率下的振型。

2 轉子機構有限元模型建立

2.1 轉子機構總成三維建模

應用Autodesk_Inventor三維軟件對異步電機轉子機構進行三維建模,異步電機轉子機構主要由電機軸、軸承套、屏板、端環和轉子鐵心組成,具體裝配關系如圖1所示,轉子鐵心與軸過盈配合,軸總長為802mm,最大外徑為φ60mm,重22.6kg,轉子鐵心最大外徑為φ110mm,寬度為150mm,軸承套與軸過盈配合,為了仿真計算方便,本模型忽略倒角等對整體受力影響不大的小特征[4]。

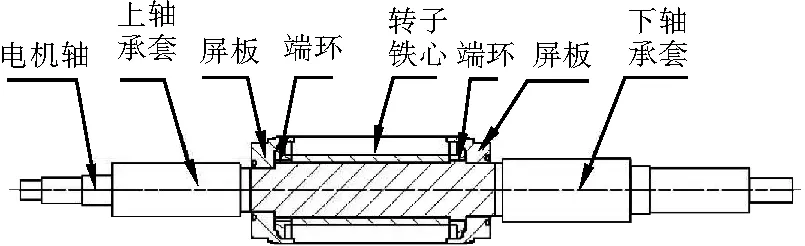
圖1 轉子機構

2.2 材料選擇

異步電機轉子機構的模態特性除本身結構外,還與各零件材料屬性有著密切關系,本文根據轉子機構各零件真實材料,通過Autodesk_Inventor三維軟件對各零件賦予材料屬性,保證有限元仿真準確。各材料屬性如表1所示。

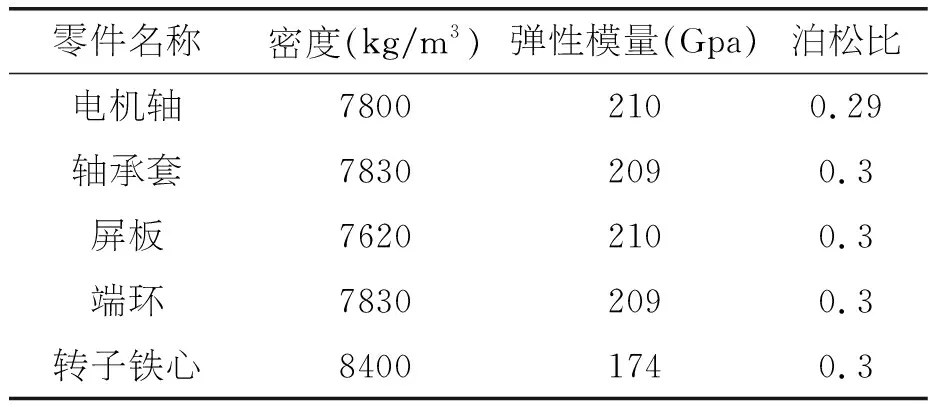
表1 轉子機構各零件材料屬性

2.3 邊界條件設置

考慮到電子轉子機構工作環境較為復雜,為使模態仿真分析更接近實際情況,根據異步電機轉子機構各零件實際裝配關系,軸承套與軸之間設置過盈配合,過盈量為0.01mm,轉子鐵心與軸之間設置過盈配合,過盈量為0.012mm,在上下軸承套上設置彈性約束。

2.4 網格劃分

模型使用高品質單元創建網格,網格平均元素大小為0.08,網格數量267370個,節點數量506258個,分級系數1.5,網格最大扭曲度為60deg,具體如圖2所示。

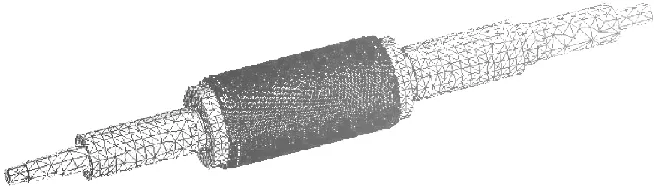
圖2 轉子機構有限元模型

3 轉子機構模態分析

模態分析可以獲得轉子機構在一定頻率范圍內的振動特性,在實際電機工作激振頻率作用下,前幾階頻率響應占較大的權值,另外電機振動主要也是由轉子機構的低階模態引起,因此,對轉子機構模態分析結果只提取前8階固有頻率及模態振型云圖,具體如圖3、表2所示。

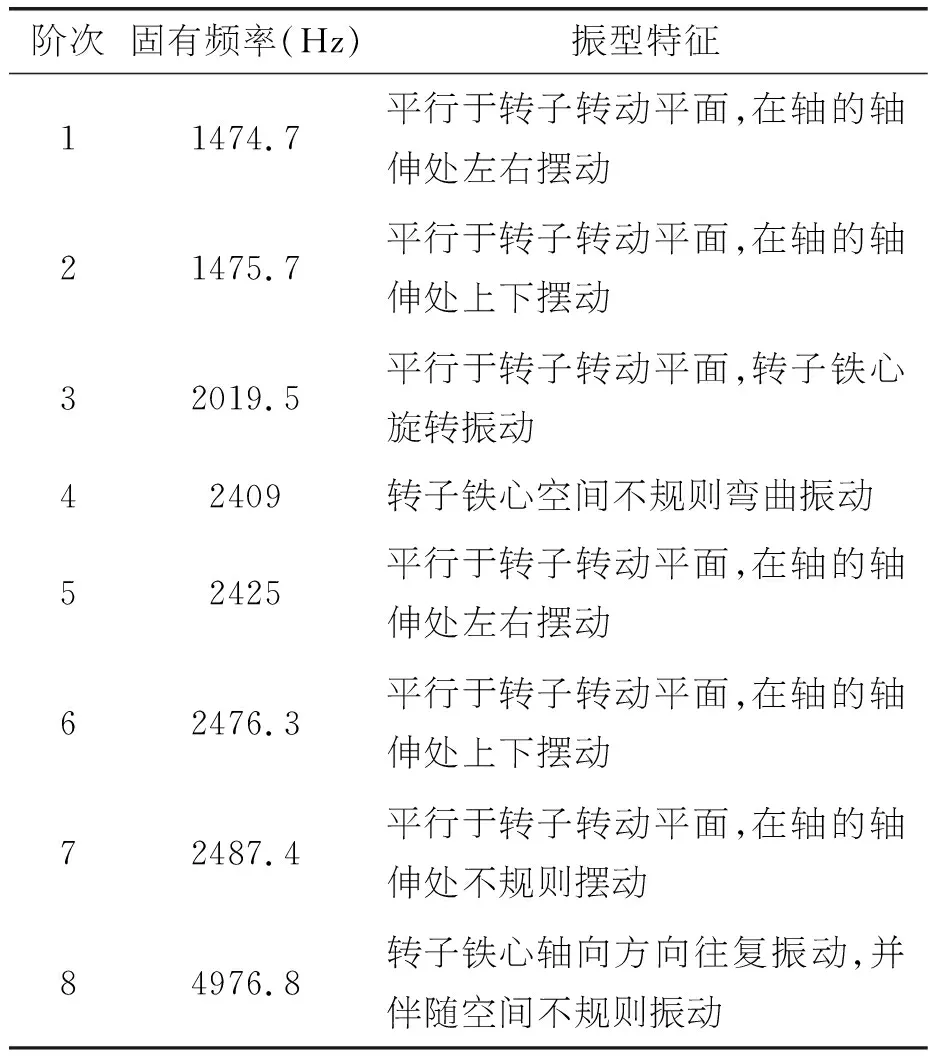
表2 轉子機構前8階模態頻率及振型描述

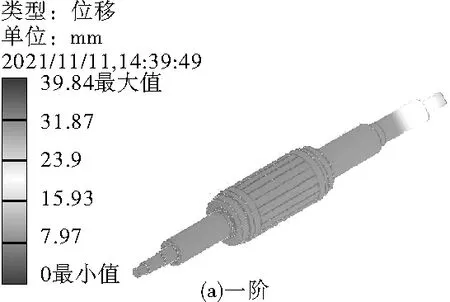
圖3 轉子機構前8階模態振型云圖

由圖3模態振型云圖可知,轉子機構前8階模態固有頻率分布在1474～4977Hz之間,隨著階次升高對應的固有頻率也在增加,值得一提的是,1、2階固有頻率基本一致,只差1Hz,其原因在于,1、2階模態振型表現在長軸軸伸處,并且幾乎在同一平面內振動,1階振型X方向最大位移為30.33mm,Y方向最大位移為25.56mm,而2階振型X方向最大位移為25.54mm,Y方向最大位移為30.34mm。3階模態振型在轉子鐵心旋轉振動;4階模態振型表現為轉子鐵心彎曲振動,X方向最大位移為29.32mm,Y方向最大位移為27.98mm。5、6、7階振型表現在短軸軸伸處,并且振動形式與1、2階相同。8階振型表現在轉子鐵心軸向方向往復振動,并伴隨XOY平面振動,X方向最大位移為5.49mm,Y方向最大位移為5.99mm,Z方向最大位移為39.76mm。

由電機轉子與頻率之間的關系得[5]

f=Pn/60

(5)

4 結語