非線性Schr?dinger方程的算子分裂配點格式
姚夢麗, 田朝薇, 翁智峰
(華僑大學 數學科學學院, 福建 泉州 362021)
Schr?dinger方程是量子力學領域的基本方程,對物理領域的研究具有深遠的意義.非線性Schr?dinger方程(NLS方程)在量子力學、非線性光學、電磁學、等離子理論、固體物理等領域中有著廣泛的應用.考慮以下NLS方程的初邊值問題,即
(1)
式(1)中:i為虛數單位;a,b,ρ,β均為常數;α(x),v(x)均為已知函數;u為未知函數.
眾所周知,NLS方程滿足質量守恒和能量守恒,有
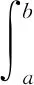
(2)
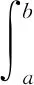
(3)
式(2),(3)中:M(t)為質量函數;E(t)為能量函數.
Schr?dinger方程作為一類重要的量子力學方程,在實際復雜的系統中,由于包含復數且為耦合的問題,其精確解往往不容易求得.因此,對其進行數值求解具有重要意義.許多研究者設計了有效的數值算法求解非線性Schr?dinger方程.孫傳志等[1]研究NLS方程的幾種差分格式.王廷春等[2]用緊致有限差分格式求解非線性耗散Schr?dinger方程.Gong等[3]采用Fourier擬譜方法構造二維NLS方程的能量和質量守恒格式.Cui等[4]用標量輔助變量(SAV)方法構造NLS方程的任意高階保結構指數Runge-Kutta方法.Feng 等[5]研究NLS方程的高階守恒SAV-Gauss配置有限元格式.張法勇等[6]研究帶五次項的NLS方程的守恒差分格式.Wang等[7]用兩層網格有限元方法對NLS方程進行超收斂性分析.Wang等[8]采用伽遼金有限元法求解阻尼NLS方程.Hu等[9]采用牛頓迭代Crank-Nicolson有限元方法求解NLS方程.Chen等[10]采用兩層網格有限體積元法求解NLS方程.以上方法都是基于網格剖分思想求解NLS方程數值解問題.最近,一種新型的無網格方法重心插值配點法廣泛應用于求解微分方程初邊值問題.重心插值配點法具有計算格式簡單、精度高、程序實施方便、節點適應性好等特點,特別使用Chebyshev節點的重心Lagrange插值公式可以有效克服Runge現象.目前,重心插值配點法已被推廣到求解高維Fredholm積分方程[11]、耦合Burgers方程[12]、粘彈性波方程[13]、Allen-Cahn方程[14-16]、Cahn-Hilliard方程[17]、Black-Scholes方程[18]、分數階電報方程[19]等.
算子分裂法[20-22]將復雜的問題分解成幾個簡單的子問題,并根據子問題的性質采用不同的求解方法,用算子分裂格式將子問題結合起來得到原問題的解,可降低原問題的求解規模,此方法廣泛應用于復雜非線性模型的數值求解中.基于此,本文提出一種非線性Schr?dinger方程的算子分裂配點格式.
1 重心Lagrange插值配點格式
1.1 重心Lagrange插值
設有插值節點xj和一組對應的實數gj(j=0,1,…,m),采用多項式插值,則在次數不超過m的多項式空間可以找到唯一的插值多項式p(x),滿足p(xj)=gj.將p(x)寫成Lagrange插值公式,即
(4)
式(4)中:Lj(x)為Lagrange插值基函數,滿足
(5)
以及
(6)
令
l(x)=(x-x0)(x-x1)…(x-xm),
(7)
定義重心插值權wj為
(8)
則Lagrange插值基函數Lj(x)可表示為
(9)
將式(9)代入式(4),可得
(10)
當p(x)=1時,有恒等式
(11)
用式(10)除以式(11),可得重心Lagrange插值公式為
(12)
由式(8)可知:重心插值權僅依賴插值節點的分布,因此,對于一些特殊的節點分布可以簡化重心插值權.特別地,當選擇Chebyshev點族時,可保證重心Lagrange插值具有良好的數值穩定性.
利用重心插值逼近未知函數時均采用第二類Chebyshev節點,即
(13)
其重心Lagrange插值的重心插值權為
(14)
1.2 重心Lagrange插值微分矩陣
對區間[a,b]上的節點a=x1 (15) 由式(15),未知函數g(x)在節點x0,x1,…,xm處的p階導數表示為 (16) 將式(16)寫成矩陣形式,即 g(p)=D(p)g. (17) 由文獻[23]可知,一階和二階微分矩陣元素的計算公式為 (18) 通過數學歸納法,可得p階微分矩陣的遞推公式為 (19) 將式(1)改寫為 iut=L(u)+N(u). (20) 式(20)中:L(u)=-ρΔu;N(u)=-v(x)u-β|u|2u. 算子分裂法的本質是將方程(20)分為兩個子問題,即 線性部分SA:iut=L(u)=-ρΔu, (21) 非線性部分SB:iut=N(u)=-v(x)u-β|u|2u. (22) 式(21),(22)中:SA和SB分別為方程(21)和方程(22)的精確解,可得Strang算子分裂格式為 (23) 設空間節點xj(j=0,1,…,m)為Chebyshev節點,時間節點tk=kτ(k=0,1,2,…,n). 首先,在空間方向上采用重心Lagrange插值配點法,可得半離散格式為 (24) 將式(24)寫成矩陣形式,即 i(uh(t))t=-ρD(2)uh(t), (25) 式(25)中:uh(t)=[u0(t),u1(t),…,um(t)]′. (26) 因此,有 (27) 方程(22)采用解析求解,即 (28) 則算子分裂格式為 (29) 考慮線性子問題的空間半離散格式(24)的相容性分析.設p(x)為u(x)的Lagrange插值函數,滿足p(xj)=u(xj),j=0,1,…,m.定義誤差函數r(x)為 r(x)=u(x)-p(x). (30) 引理1[19]假設u∈Cm+1(a,b),則有 式中:lx表示區間[a,b]的一半.類似地,可得 為了給出線性子問題SA的空間半離散格式(24)的相容性分析,首先,定義算子Γ為 (31) 定理1如果u∈C1([0,T])∪Cm+1([a,b]),有 證明:由式(21)和式(24),可得 Γu(x,t)-Γu(xj,t)=iut(x,t)+ρuxx(x,t)-iut(xj,t)-ρuxx(xj,t)= (32) 式(32)中: R1=iut(x,t)-iut(xj,t),R2=ρuxx(x,t)-ρuxx(xj,t). (33) 對于R1,有 R1=iut(x,t)-iut(xj,t)=i(ut(x,t)-ut(xj,t))=irt(xj,t). (34) 由引理1可得 (35) 類似地,可得 (36) 將式(35),(36)代入式(32)即可,證畢. 定義L∞誤差和L2誤差分別為 式中:ui為點xi處的精確解;Ui為點xi處的數值解. 比較重心Lagrange插值配點格式和有限差分格式的數值結果,以驗證插值配點格式的有效性及高精度.ρ=1,β=1,選取帶右端項的真解u(x,t)=costsin πx,0≤x≤1,右端項為f(x)=-isintsin πx-π2costsin πx+|costsin πx|2costsin πx,初始條件為u(x,0)=sin πx,0≤x≤1, 邊界條件為u(0,t)=u(1,t)=0,0≤t≤1,勢函數v(x)=0. 固定時間步長(τ=10-4),改變空間節點數(M),重心Lagrange插值配點格式和有限差分格式的誤差,如表1所示.由表1可知:算例1的重心Lagrange插值配點格式選取6個節點差值即可達到10-5量級,而有限差分格式選取256個節點差值才能達到10-5量級,這表明重心Lagrange插值配點格式在空間上用較少的點可達到更高的精度. 表1 重心Lagrange插值配點格式和有限差分格式的誤差(算例1)Tab.1 Errors of barycentric Lagrange interpolation collocation scheme and finite difference scheme (example 1) 固定空間節點數(M=8),改變時間步長,重心Lagrange插值配點格式的誤差及時間收斂階,如表2所示.表2中:Rt,1,Rt,2分別為L∞誤差和L2誤差的時間收斂階.由表2可知:基于重心Lagrange插值配點格式的NLS方程在時間上是二階精度. 表2 重心Lagrange插值配點格式的誤差及時間收斂階(算例1)Tab.2 Errors and time convergence orders of barycentric Lagrange interpolation collocation scheme (example 1) 不同數值格式的空間收斂階,如圖1所示.圖1中:Rs為空間收斂階.由圖1可知:有限差分格式的空間收斂階是二階精度;重心Lagrange插值配點格式的空間收斂階滿足指數收斂的性質. 圖1 不同數值格式的空間收斂階(算例1)Fig.1 Spatial convergence orders for different numerical schemes (example 1) 算例2的重心Lagrange插值配點格式和有限差分格式的誤差(τ=10-4),如表3所示.由表3可知:算例2的重心Lagrange插值配點格式選取8個節點差值即可達到10-4量級,而有限差分格式選取128個節點差值也只能達到10-4量級,故重心Lagrange插值配點格式具有較高的精度. 表3 重心Lagrange插值配點格式和有限差分格式的誤差(算例2)Tab.3 Errors of barycentric Lagrange interpolation collocation scheme and finite difference scheme (example 2) 重心Lagrange插值配點格式的數值解和精確解(M=64,t=1),如圖2所示.不同數值格式的空間收斂階,如圖3所示.重心Lagrange插值配點格式守恒量的保持情況,如圖4所示. (a) 數值解 (b) 精確解圖2 重心Lagrange插值配點格式的數值解和精確解Fig.2 Numerical solution and exact solution of barycentric Lagrange interpolation collocation scheme 圖3 不同數值格式的空間收斂階(算例2)Fig.3 Spatial convergence orders for different numerical schemes (example 2) (a) 總質量 (b) 質量誤差 由圖2可知:NLS方程的重心Lagrange插值配點格式是穩定的.由圖3可知:有限差分格式是二階精度,重心Lagrange插值配點格式呈指數遞減.由圖4可知:基于重心Lagrange插值配點格式的NLS方程滿足質量守恒和能量守恒. 通過算例3進行孤立波的演化實驗.選取空間節點M=248,時間步長τ=10-4,對應的計算區間為[-10π,10π]×[0,T],ρ=1,β=2,選取真解u(x,t)=exp(i(2x-3t))sech (x-4t),初始條件為u(x,0)=exp(2ix)sechx,邊界條件為u(a,t)=u(b,t)=0,勢函數v(x)=0. 算例3的重心Lagrange插值配點格式的誤差及時間收斂階(M=248),如表4所示.由表4可知:算例3驗證了時間收斂階為二階精度. 表4 重心Lagrange插值配點格式的誤差及時間收斂階(算例3)Tab.4 Errors and time convergence orders of barycentric Lagrange interpolation collocation scheme (example 3) 初始孤立波波形,如圖5所示. 圖5 初始孤立波波形Fig.5 Initial isolated wave shape 重心Lagrange插值配點格式的孤立波波形,如圖6所示.由圖6可知:算例3的重心Lagrange插值配點格式的孤立波波形隨時間的變化而變化,符合物理意義,而且每個時刻的波形都沒有出現震蕩,這說明該格式是穩定的. (a) t=1 (b) t=3 (c) t=5圖6 重心Lagrange插值配點格式的孤立波波形Fig.6 Isolated wave shapes of barycentric Lagrange interpolation collocation scheme 重心Lagrange插值配點格式守恒量的保持情況,如圖7所示.由圖7可知:算例3的重心Lagrange插值配點格式保持質量守恒和能量守恒. (a) 總質量 (b) 總能量圖7 重心Lagrange插值配點格式守恒量的保持情況(算例3)Fig.7 Conservation of conserved quantities of barycentric Lagrange interpolation collocation scheme (example 3) 將算子分裂格式與重心Lagrange插值配點格式相結合,提出一種求解NLS方程的有效數值格式.此外,對方程的非線性部分采用解析求解,降低非線性迭代的計算量,提高計算效率,并給出線性子問題空間半離散格式的相容性分析.最后,通過數值算例驗證格式的高精度和有效性.與經典的有限差分格式進行比較可知,文中格式可用較少的點達到較高的精度.今后,可將該方法推廣到其他非線性微分方程,為解決同類問題提供一種高精度數值求解方法,如耦合的非線性Schr?dinger方程、時間分數階非線性Schr?dinger方程等.2 基于重心Lagrange插值的NLS方程算子分裂格式
2.1 Strang算子分裂法
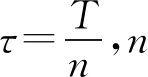
2.2 SA和SB的數值逼近
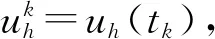
3 相容性分析

iut(x,t)-iut(xj,t)+ρuxx(x,t)-ρuxx(xj,t)=R1+R2.4 數值算例
4.1 算例1
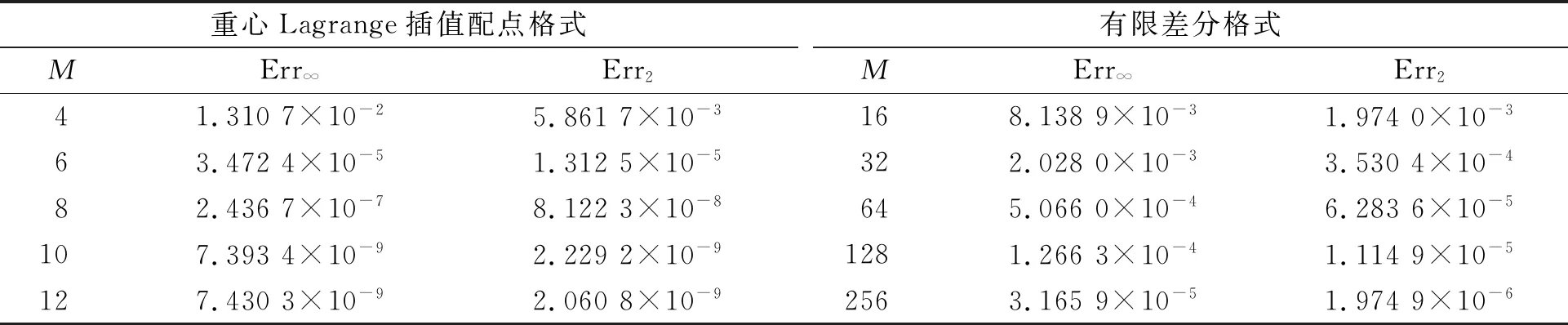

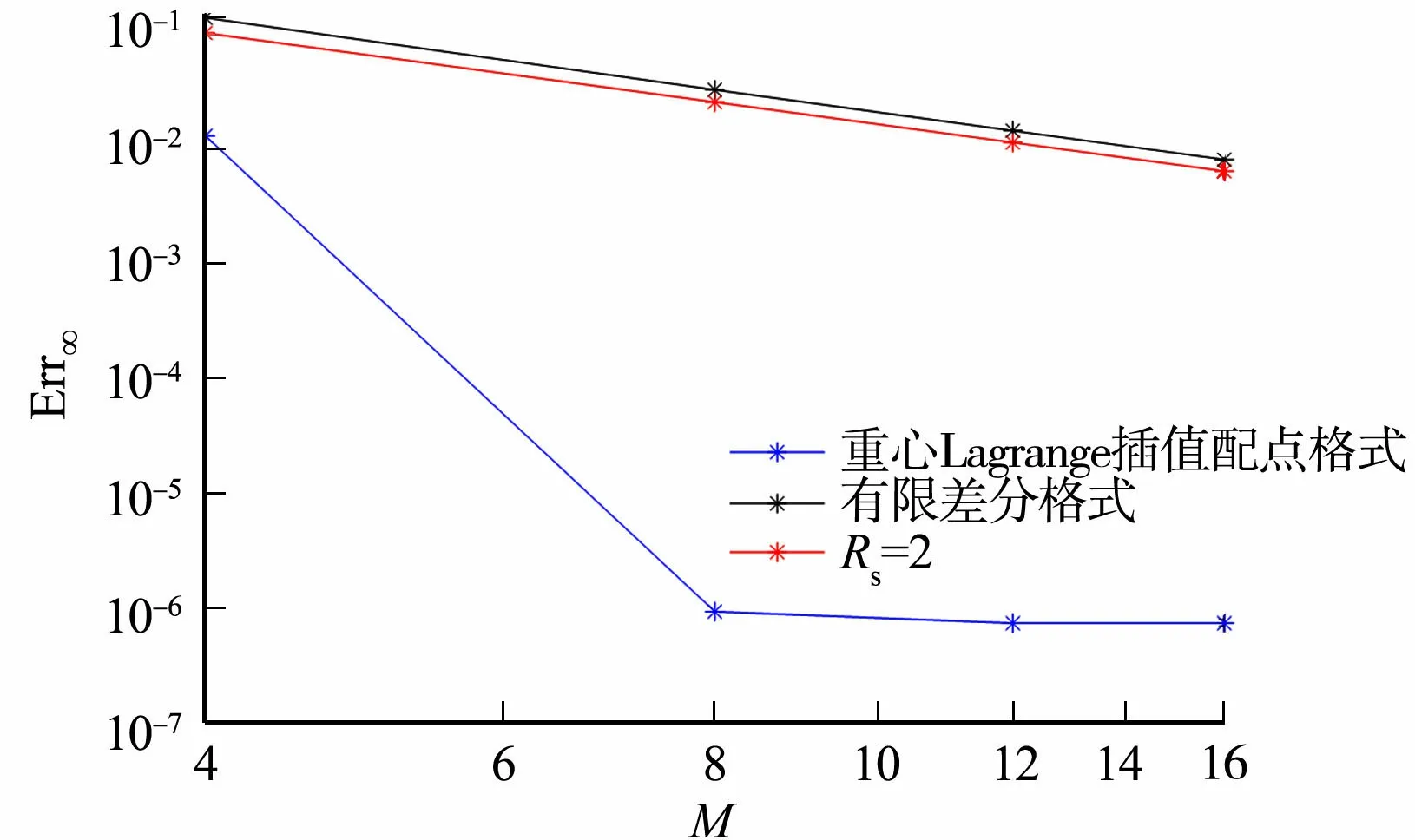
4.2 算例2
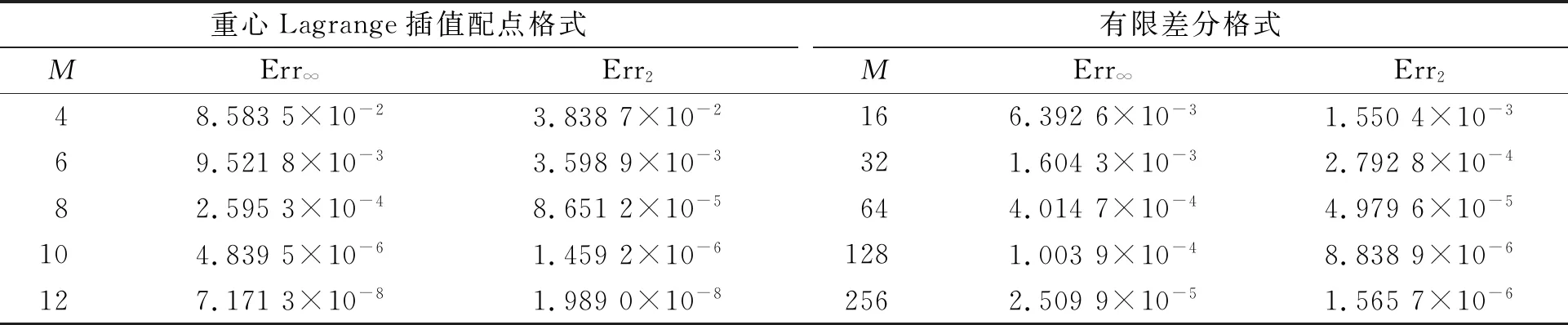
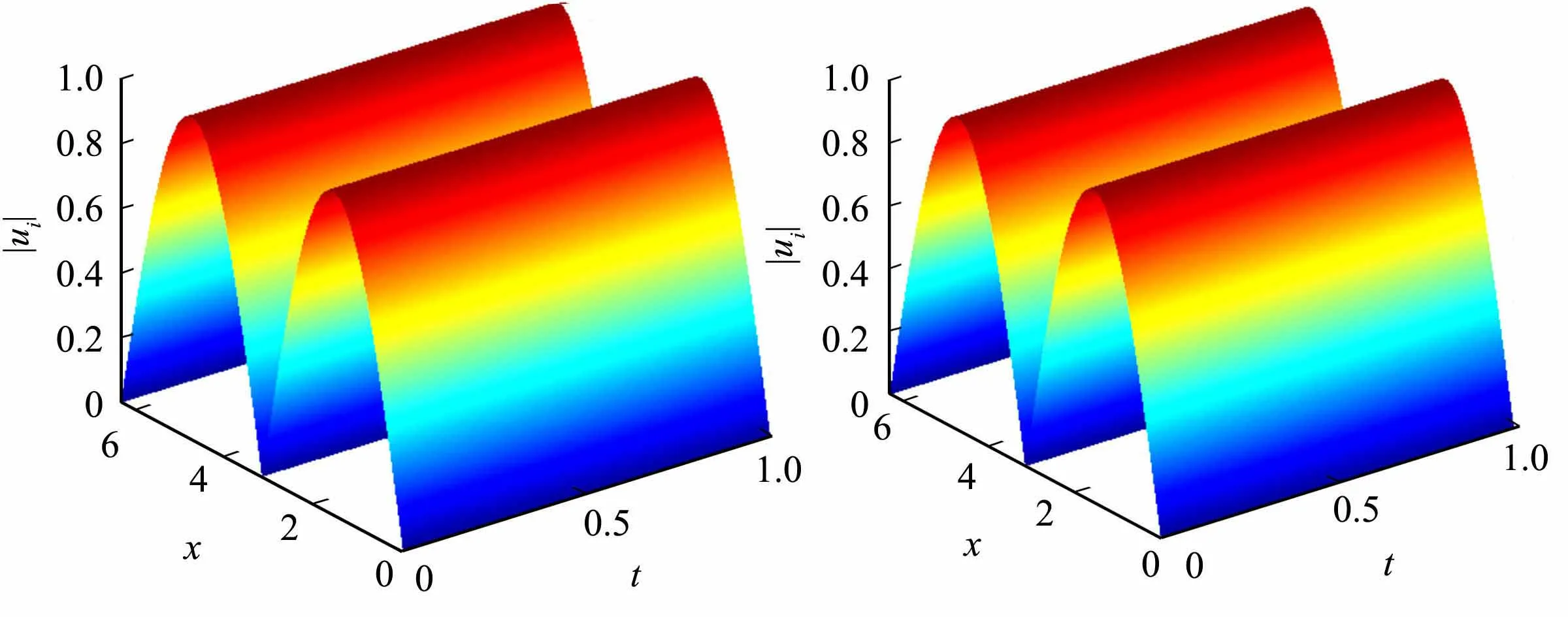

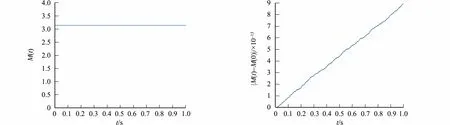
4.3 算例3

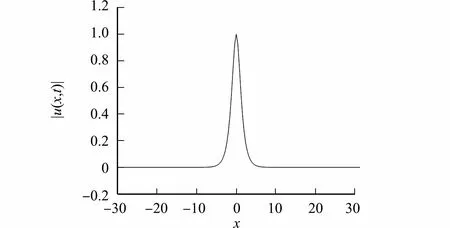
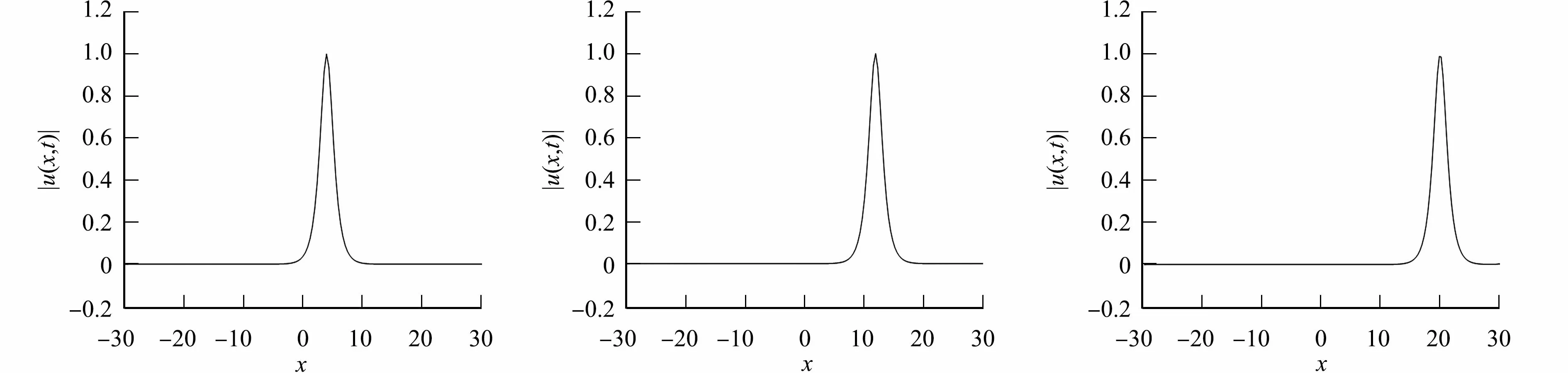

5 結束語

