非局部Swift-Hohenberg方程的積分因子龍格庫塔格式

汪亞楠, 蔡耀雄

(華僑大學 數學科學學院, 福建 泉州362021)

Swift-Hohenberg(SH)模型[1]最初是由Swift和Hohenberg在研究Rayleigh-Bénard對流時引入的,并且已經成為導致復雜模式形成的非線性動力系統的范例之一,其研究成果被廣泛應用于復雜流體和生物組織[2-3].近年來,隨著流體力學、反應擴散化學和生物學等學科的發展,非局部SH模型的研究吸引了眾多學者的關注.Roberts[4]指出,將二維局部SH模型用作特定物理系統中空間模式演化的可靠模型是不夠的,應使用非局部SH模型.2014年,Morgan等[5]首次提出帶有非局部非線性項的SH模型,即

ut=-(Δ+1)2u+εu-uG*u2, (x,t)∈Ω×(0,T].

(1)

非局部項G*u2的定義為

卷積核G滿足以下3個條件：1)G(x)≥0,對于任意的x∈Ω;2)G是Ω-周期性;3)G(x)=G(|x|)

是一個給定的徑向對稱函數.

非局部SH方程(式(1))可看作能量函數E(u)的L2梯度流,有

(2)

關于局部SH方程的理論和數值研究已有大量的優秀成果[6-7],而關于非局部SH方程的研究工作還十分有限.非局部SH方程中的非局部和非線性項給研究帶來巨大挑戰.Firth等[8]提出非線性光學系統的非局部模型.Purwins等[9]提出介質氣體放電動力學的非局部模式.Du等[10]提出非局部算子的向量演算.Zhang等[11]提出一個帶有拉格朗日乘子的守恒型非局部 SH方程.Weng等[12]利用傅里葉譜方法求解帶有非局部非線性項的SH方程.

近年來,作為求解偏微分方程的有效數值方法,積分因子龍格庫塔法受到廣泛關注.Ju等[13]提出關于半線性拋物方程的保極值原理的積分因子龍格庫塔方法.Ahmed等[14]提出關于非齊次邊界條件系統的高階積分因子法.Zhang等[15]提出保守Allen-Cahn方程的顯式三階保結構格式.Nan等[16]提出求解非局部Allen-Cahn方程的高階極值原理積分因子龍格庫塔方法.基于此,本文結合積分因子龍格庫塔法和譜方法[17]對式(1)進行有效求解,并提出4種快速有效求解非局部Swift-Hohenberg方程的數值格式.

1 數值格式

1.1 預備知識

空間區域Ω=[-a,a]2上的網格剖分為

為了求解周期邊界條件下的非局部SH方程(式(1)),基于譜方法的相關理論,采用傅里葉級數逼近{ui,j}進行空間離散求解.

(3)

(4)

引理1[12]對于任意的網絡函數u∈Mh,擴散算子(Δ+1)2u及非局部卷積算子G*u的譜離散形式分別為

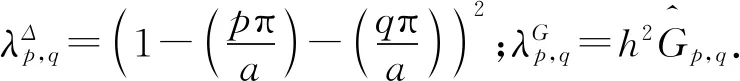
1.2 顯式穩定性積分因子龍格庫塔求解非局部SH方程

相較于傳統的強穩定性龍格庫塔方法,強穩定性積分因子龍格庫塔可避免線性算子的時間步長限制,但由于非線性算子帶來的時間步長限制,需要引入一種無時間步長限制的保界格式.

顯式穩定性積分因子龍格庫塔法(eSIFRK)[13,18-19]是一種顯性格式且保極值原理的離散方法,其時間步長的約束僅取決于非線性項,故時間步長大小的選擇與空間網格大小無關.

采用顯式穩定性積分因子龍格庫塔法,分別建立求解式(1)的一步一階、二步二階、三步三階、四步四階的無時間步長限制的保界格式.

積分因子(IF)法[20]的步驟如下.

首先,將式(1)改寫為

ut=Lu+f(u).

(5)

式中：Lu=-(Δ+1)2u;f(u)=εu-uG*u2.

其次,引入新變量v,定義為

v=e-Ltu.

(6)

式(6)中：e-Lt為積分因子.

然后,式(5)兩邊同時乘以e-Lt,可得

e-Ltut-Le-Ltu=e-Ltf(u).

(7)

注意到vt=e-Ltut-Le-Ltu,則式(7)可簡化為

vt=e-Ltf(eLtv).

(8)

根據文獻[13],可得式(8)的s步穩定性積分因子龍格庫塔格式為

u(0)=un,

(9)

(10)

un+1=u(s).

(11)

給定s=1,2,3,4,可得一步一階顯式穩定性積分因子龍格庫塔格式eSIFRK(1,1)為

un+1=eτL[un+τf(un)].

二步二階顯式穩定性積分因子龍格庫塔格式eSIFRK(2,2)為

.

三步三階顯式穩定性積分因子龍格庫塔格式eSIFRK(3,3)為

四步四階顯式穩定性積分因子龍格庫塔格式eSIFRK(4,4)為

2 數值算例

數值解的L2范數誤差ErrL2(τ,h)為

數值解的最大誤差Errmax(τ,h)為

2.1 算例1

為了驗證時間收斂階,算例1的空間區域Ω=[-20,20]2,初始值為

u0(x,y)=0.01×(cos πx+cos πy+2cos 0.25πy).

表1 不同時間步長下的時間誤差和時間收斂階Tab.1 Time errors and time convergence rates at different time

由表1可知：時間收斂階都達到了預期精度.

2.2 算例2

算例2考慮帶有隨機初始擾動的非局部SH方程,其空間區域Ω=[-64,64]2,初始值為

u0(x,y)=0.07+0.001×rand(x,y).

式中：rand(x,y)表示取值在[-1,1]的隨機數.

設置系數ε=0.035,δ=0.5,固定空間步長h=1,時間步長τ=1.

采用四步四階顯式穩定性積分因子龍格庫塔格式可得不同時刻數值解圖像和能量圖(T=2 000),如圖1所示.由圖1可知：能量是遞減的.

(a) T=0 (b) T=300 (c) T=500 (d) T=700

2.3 算例3

為了研究數值解與能量的變化,算例3空間區域Ω=[-64,64]2,初始值為

設置系數ε=0.035,δ=0.5,固定空間步長h=1,時間步長τ=0.1.

采用四步四階顯式穩定性積分因子龍格庫塔格式可得不同時刻數值解圖像及能量圖(T=1 000),如圖2所示.由圖2可知：能量是遞減的.

(a) T=0 (b) T=5 (c) T=20 (d) T=50

2.4 算例4

考慮空間區域Ω=[-150,150]2時液體晶體的生長,初始值為

采用四步四階顯式穩定性積分因子龍格庫塔格式可得不同時刻數值解圖像及能量圖(T=1 000),如圖3所示.由圖3可知：隨著時間的推移,微晶相互碰撞并開始形成晶界;當T=1 000時,能量隨著時間逐漸減小達到穩態.

(a) T=0 (b) T=50 (c) T=200 (d) T=400

3 結束語

結合積分因子龍格庫塔法和傅里葉譜方法求解非局部SH方程,得到一種快速有效的數值格式,數值算例表明文中算法具有較好的穩定性及較高的準確性,且滿足能量遞減性質.