地下裝配式大直徑組合筒倉倉壁穩定性分析

張 昊 王馨康 諶 磊

（河南工業大學土木工程（建筑）學院，河南 鄭州 450001）

關鍵字：地下倉；穩定性分析；組合圓筒殼；等效屈曲；鋼板-混凝土結構

0 引言

糧食安全事關國家安全。隨著國內、國際形勢的變化，我國對糧食儲備安全和技術手段的要求也越來越高，而地下糧倉在節能節地、綠色環保、優質儲糧等方面有著顯著優勢，是我國建立綠色儲糧新體系的重要技術支撐，也是今后糧倉建設的發展方向之一［1］。預制裝配式鋼板-混凝土地下糧倉采用內襯鋼板防水，實現結構防水受力一體化，同時可通過逆作法解決地下現澆組合結構土方工作量大、施工工期長的問題，如圖1 所示。目前，地下裝配式組合結構已應用于實際工程中［2-4］，但隨著地下糧倉單倉儲量的不斷增大，倉體埋深和倉壁直徑不斷增加，如何對水土壓力作用下的裝配式組合倉壁穩定性進行驗算，成為當前進一步推廣裝配式地下糧倉亟須解決的問題。

圖1 預制裝配式地下糧倉倉壁

裝配式地下結構接頭是影響結構整體受力性能的關鍵部位，國內外對類似地下結構進行了大量研究。葉亮等［5］對一種新型型鋼-混凝土組合接頭的抗彎性能進行試驗研究；焦勇強等［6］總結了整體預制拼裝式綜合管廊常用的接頭型式及防水構造的優缺點及適用范圍，為綜合管廊接頭的設計與改進提供參考；Liu 等［7］通過試驗和數值分析，對比采用預制側壁節點與現澆側壁節點的地鐵車站在低周往復荷載作用下的抗震性能，為地下混凝土結構設計提出節點最優的形狀和設置位置。在裝配式地下糧倉方面，張昊等［8］對地下組合糧倉豎向接頭的受彎性能進行研究，結果表明，接頭處傳力鋼板與內側止水鋼板可共同發揮抗拉作用；王振清等［9］在裝配式地下糧倉鋼板-混凝土組合倉壁軸壓試驗的基礎上進行非線性有限元分析，并給出組合倉壁軸壓峰值荷載簡化計算式。

綜上所述，國內外對裝配式地下組合筒倉倉壁穩定性研究較少，本研究對地下裝配式鋼板-混凝土倉壁在外表面均布荷載作用下的穩定性問題進行研究，為工程應用提供理論依據及設計參考。

1 有限元法分析

為驗證有限元法計算地下倉倉壁屈曲荷載的可靠性，利用有限元軟件Abaqus 建立大直徑無接頭混凝土倉壁數值模型進行線性屈曲分析。

地下倉在施工和使用階段存在多種工況，在施工階段，當預制的組合倉壁管片全部拼裝完成，且還沒有施工倉底漏斗和倉頂蓋時為最不利工況。取地下糧倉倉壁最底部高度為1 m 的倉壁圓筒為研究對象，并近似認為空倉（最不利工況）時，倉壁承受的外側徑向水土側壓力為均布荷載，且不考慮倉底、倉頂對倉壁的約束作用。

建立地下倉壁的穩定性分析數值模型，以倉壁徑向為X軸、環向為Y軸、高度方向為Z軸，建立空間柱坐標系。倉壁圓筒模型結構對稱，外部壓力荷載也對稱，利用對稱性建立半個圓筒有限元模型，倉壁模型的參數及尺寸見表1。經網格收斂性分析后，網格尺寸取為0.04 m、混凝土材料采用C3D8R實體單元。地下糧倉倉壁主要以受壓為主，鋼筋與混凝土在彈性受壓階段協同工作，將其視為一個整體，忽略線性屈曲分析中配筋對倉壁整體穩定性的影響。在倉壁模型兩端截面施加對稱面約束以限制在Y方向的位移和繞X軸、Z軸方向的轉動，利用約束方程控制兩個端面內側節點在X方向的位移，在倉壁頂面和底面施加Z方向的位移約束，在倉壁模型外表面施加單位大小的徑向均布荷載。

表1 地下組合倉壁數值模型參數

本研究使用Lanczos 法對250 mm 厚現澆混凝土倉壁進行屈曲分析，得到其特征值為48 575.3，即其屈曲荷載數值解為48.575 kPa，屈曲模態如圖2所示。

圖2 現澆地下鋼板-混凝土倉壁屈曲模態

Timoshenko［10］給出徑向均布荷載作用下單層圓筒殼屈曲荷載的表示，見式（1）。

式中：qcr為薄壁圓筒的屈曲荷載；E、I、μ分別為材料的彈性模量、截面慣性矩和泊松比；R為圓筒截面中心點到筒壁圓心的距離。

通過該公式可計算得到屈曲荷載理論解。屈曲荷載數值解與理論解的對比結果見表2，證明利用有限元法對地下組合倉壁進行屈曲分析是準確、可靠的。

表2 現澆混凝土倉壁屈曲荷載

2 裝配式地下筒倉倉壁穩定性分析

為進一步研究在大直徑裝配式地下組合倉壁設計中接頭剛度對倉壁整體穩定性的影響，對內徑為25 m、徑厚比為100∶1 的裝配式組合倉壁進行分析。

2.1 接頭設計

裝配式鋼板-混凝土組合倉壁預制構件通過豎向接頭連接成環，考慮實際工程需求，本研究設計的喇叭形豎向接頭如圖3 所示。該接頭由鋼樁、外側包邊鋼板、腹板、內側包邊鋼板、止水鋼板、外側包邊延伸鋼板組成。喇叭形開口方便施焊，同時接頭空腔內可灌注防水材料，與鋼樁翼緣板、止水鋼板組成三道防水層。其中，內側包邊鋼板、外側包邊鋼板與腹板厚度為20 mm，外側包邊延伸鋼板厚度為5 mm，鋼樁翼緣板與止水鋼板厚度為t0，通過調整t0的大小可控制接頭抗彎剛度的大小。

圖3 地下裝配式大直徑組合倉壁喇叭形豎向接頭

2.2 組合倉壁穩定性分析

已有的研究［8-9］證明，通過在鋼板上設置間距合理的栓釘能保證鋼板混凝土組合構件在彈性受力階段，其鋼板與混凝土可協同受力變形，兩種材料之間可近似看作是剛性連接。

根據前文設計的倉壁豎向接頭形式，建立直徑為12.5 m、徑厚比100∶1的地下裝配式鋼板-混凝土倉壁數值模型，模型參數參見表1。倉壁混凝土采用C3D8R 實體單元，內側鋼板與豎向接頭鋼板選擇S4R 殼單元，接頭材料屬性與倉壁內側鋼板相同。裝配式組合倉壁模型網格尺寸控制為0.1 m，其邊界條件與加載方式與現澆混凝土倉壁相同。內側鋼板、接頭鋼板與混凝土之間的剛性連接通過共用節點實現。

對接頭抗彎剛度為2.16×107～3.24×107N·m2的裝配式鋼板-混凝土倉壁進行穩定性分析，屈曲荷載數值解見表3。接頭剛度不同的裝配式組合倉壁一階屈曲模態如圖4 所示。由圖4 可知，模型ACSW-1～ACSW-8 均為“橢圓形”整體屈曲，與文獻［10］中均布荷載作用下單層薄壁圓筒一階屈曲模態一致。

表3 地下裝配式鋼板-混凝土倉壁屈曲分析數值解

圖4 地下裝配式鋼板-混凝土倉壁一階屈曲模態

對與裝配式鋼板-混凝土組合倉壁有相同幾何尺寸和材料屬性的現澆（無接頭）鋼板-混凝土倉壁進行穩定性分析，得到的一階屈曲模態為與圖4 相似的“橢圓形”，現澆組合倉壁的屈曲荷載數值解為84.210 kPa。

組合倉壁截面抗彎剛度為D1，豎向接頭截面抗彎剛度為D2，現澆組合倉壁屈曲荷載為Pcr1，裝配式組合倉壁的屈曲荷載為Pcr2。定義剛度比γ=D2/D1，荷載比λ=Pcr2/Pcr1，得到剛度比-荷載比曲線如圖5所示。由圖5 可知，隨著剛度比γ的增大，荷載比λ逐漸增大但增幅逐漸減小。當γ不小于1 時，裝配式鋼板-混凝土組合倉壁屈曲荷載與現澆組合倉壁屈曲荷載之比λ不小于1，即此時裝配式組合倉壁屈曲荷載不小于現澆組合倉壁，此時喇叭形豎向接頭鋼板厚度為9.04 mm。

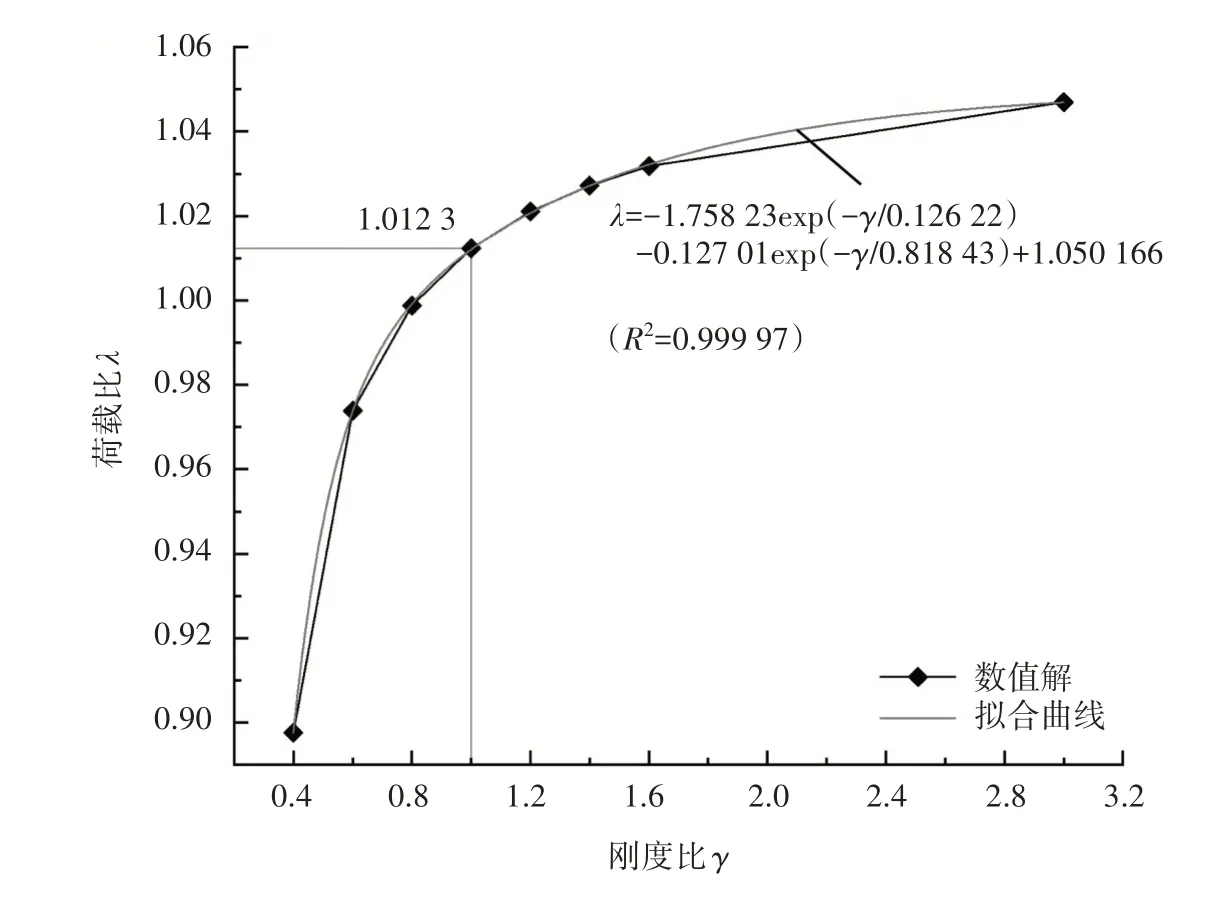
圖5 地下裝配式鋼板-混凝土倉壁剛度比-荷載比關系曲線

對圖4 中各點進行擬合，得到荷載比λ與剛度比γ的擬合曲線關系式，見式（2）。

通過式（2）可將裝配式組合倉壁屈曲荷載等效為現澆組合倉壁進行整體穩定性驗算。首先，根據裝配式組合倉壁的內徑、倉壁外層混凝土厚度、倉壁內襯鋼板厚度和材料參數建立復合圓筒殼有限元數值模型，計算其在均布荷載作用下的屈曲荷載Pcr1；其次，計算裝配式組合倉壁豎向接頭的抗彎剛度D2和組合倉壁截面抗彎剛度D1，將接頭抗彎剛度D2與組合倉壁抗彎剛度D1之比γ代入到式（2）中，計算得到荷載比λ；最后，代入λ=Pcr2/Pcr1，得到裝配式組合倉壁在徑向均布荷載作用下的極限穩定承載力。

3 結語

本研究對采用喇叭形豎向接頭的地下大直徑裝配式鋼板-混凝土筒倉組合倉壁在徑向均布荷載作用下的整體穩定性進行分析，得到以下3個結論。

①采用喇叭形豎向接頭的鋼板-混凝土倉壁的一階屈曲模態為“橢圓形”整體屈曲，與現澆混凝土倉壁和無接頭鋼板-混凝土組合倉壁的一階屈曲模態一致。

②通過改變豎向接頭抗彎剛度，得到大直徑裝配式鋼板-混凝土組合倉壁的剛度比-荷載比關系曲線，結果表明：當接頭抗彎剛度不小于組合倉壁截面抗彎剛度時，裝配式鋼板-混凝土倉壁的屈曲荷載不小于現澆鋼板-混凝土組合倉壁。

③通過剛度比-荷載比曲線，得到可用于計算地下裝配式鋼板-混凝土倉壁極限穩定承載力的關系式。