輪軌滑動對高速鐵路扣件彈條振動特性的影響

康 熙, 陳光雄, 何俊華, 宋啟峰, 祿 盛

(1. 重慶郵電大學 先進制造工程學院,重慶 400065;2. 西南交通大學 機械工程學院 摩擦學研究所,成都 610031)

鋼軌扣件是鐵路軌道系統重要的組成部分之一,它將鋼軌固定在軌枕或軌道板上。當扣件正常工作時,軌距被限定在合理的范圍內,并且輪軌作用力可以正常傳遞到軌下結構中。扣件彈條斷裂是一種常見的扣件失效形式,嚴重影響了列車的運行安全性和穩定性[1],該現象頻繁出現于高鐵[2]和地鐵[3]線路中。高速列車運營速度較高,輪軌作用相對劇烈。在高鐵線路上某些區段一旦出現大量扣件彈條斷裂失效,將嚴重威脅到列車的行車安全。

對于扣件彈條斷裂失效問題,學者們開展了大量的研究。Ling等[4]通過測試地鐵車輛通過軌道時的動態響應,發現鋼軌波磨激勵的高頻輪軌振動會加速扣件彈條的疲勞失效。余自若等[5]對X2型彈條扣件系統進行有限元建模,分析了扣壓力、鋼軌橫向作用力、荷載頻率對彈條疲勞失效的影響,發現過擰、鋼軌橫移會導致彈條疲勞壽命降低。Xiao等[6]通過仿真和試驗研究了地鐵e型彈條扣件失效機理,發現不恰當的安裝方式是導致該型扣件失效的主要原因。此外,鋼軌波磨激勵的共振也可導致彈條斷裂。Hasap等[7]通過有限元仿真和疲勞試驗研究了扣件趾端載荷對e型彈條失效的影響,發現較低的趾端載荷可以減少沖擊對彈條疲勞壽命的影響。高曉剛等[8]測試了輪軌耦合條件下SKL彈條的組裝模態頻率,通過錘擊模態測試和有限元模態分析研究了預緊螺栓扭矩對彈條模態頻率的影響,并對彈條結構進行優化以提高其疲勞壽命。崔樹坤等[9]對W1型扣件彈條進行模態試驗,研究了0～1 000 Hz頻率內彈條的前2階模態,分析了彈條安裝狀態對固有頻率的影響。向俊等[10]基于有限元仿真,分析了WJ-7型扣件彈條的斷裂機理,分別研究了前3階車輪多邊形磨耗、曲線半徑、車速對彈條應力和疲勞壽命的影響,發現車輪多邊形化、曲線半徑減小、車速提高均會加速彈條疲勞失效。潘兵等[11]通過有限元瞬時動態仿真研究了輪軌滾滑接觸對SKL15彈條失效的影響,發現輪軌間蠕滑力飽和引起的不穩定振動頻率與彈條模態頻率接近,可能導致彈條共振,加劇損傷。Wang等[12]分別測試了地鐵列車經過鋼軌波磨區段和無波磨區段時扣件彈條的振動加速度,通過建立車輛-軌道耦合模型,研究了波磨對扣件彈條振動和危險節點處應力的影響,發現鋼軌波磨會引起彈條強迫振動,在一定的列車運行速度和波磨波長條件下,會引起彈條共振。基于有限元仿真和試驗,Liu等[13]研究了e型和Fast型扣件彈條的失效現象,并對其疲勞壽命進行評估。研究發現,有限元仿真預測的扣件彈條損傷位置與現場測試結果基本一致。基于地鐵列車-道床動力學模型,魏綱等研究了扣件失效對車軌系統動力響應的影響,發現扣件失效數量對車體加速度影響顯著,對車體和襯砌的振動信號進行監測可輔助判定扣件失效位置。黃浩志等[14]建立了空心W1型彈條實體模型,對該彈條組裝時的靜力學表現和模態進行仿真計算,發現空心彈條的固有頻率相比實心彈條顯著提高。秦俊飛等[15]分別測試了地鐵線路上行車激勵下和無載狀態下DI型扣件彈條的模態頻率,發現行車激勵下彈條模態頻率相比無載狀態下小幅減小。姜秀杰等[16]對行車載荷激勵下ω型彈條的時域響應進行模擬,在實測路譜上疊加彈條組裝模態頻率,來模擬鋼軌波磨激勵下的彈條共振響應。研究發現,當波磨激勵頻率與彈條模態頻率接近而引起共振時,彈條跟端應力增大,容易導致彈條斷裂失效。劉玉濤等[17]建立了車輛-軌道垂向耦合系統動力學模型,分析了減振型無砟軌道同一道床板板端、板中和板尾扣件彈條的疲勞損傷差異性。仿真研究發現:應力循環幅值的增大導致了板端、板尾彈條的疲勞損傷平均值大幅增加。肖洪秀等[18]通過掃描電子顯微鏡對60Si2Mn材質彈條斷口的宏觀、微觀形貌進行分析,發現疲勞源區的裂紋不平整,擴展區裂紋呈云浮狀,瞬斷區出現了明顯韌窩現象。

高速列車在上下縱坡區段通常處于牽引或制動狀態,當輪軌接觸面之間存在水油污染時,在牽引或制動工況下可能發生輪軌滑動[19]。Cui等對京廣線高速鐵路鋼軌波磨現象進行調查發現,在坡度為10.5‰的路段上存在嚴重的鋼軌波磨和扣件彈條失效現象。進一步研究發現,輪軌滑動引起的摩擦自激振動為鋼軌波磨的形成原因之一,但扣件彈條的失效機理尚不明確。

先前研究表明,特定頻率的輪軌振動會引起彈條共振,加速其斷裂失效。本文建立了車輪-鋼軌-扣件系統有限元模型,采用復特征值分析求解輪軌滑動引起的不穩定振動頻率和模態,發現輪軌飽和縱向蠕滑力引起的603 Hz不穩定振動可引起ω型扣件彈條共振。此外,該不穩定振動還可引起波長為130～190 mm的鋼軌波磨。當車輪以300 km/h在波磨鋼軌上滾動運行時,波磨激勵的強迫振動可傳遞至扣件系統中,引起彈條共振。

1 有限元模型和理論模型

1.1 車輪-鋼軌-扣件系統有限元模型

Cui等表明在京廣線高速鐵路測試區段內運營的列車類型為CRH3,在該區段內的平均運行車速為300 km/h。車輪踏面類型為S1002CN,車輪直徑為0.92 m。該區段內軌枕間距為0.65 m,鋼軌型面為CHN60。理想狀態下,在直線線路或大半徑曲線線路上,同一輪對左右車輪與鋼軌間作用力非常相似。為了減少有限元模型中的網格數量,提高計算速度,在有限元軟件ABAQUS中建立單輪-鋼軌-扣件系統模型,如圖1所示。模型網格單元類型均為C3D8I,車輪與鋼軌接觸區域的網格被細化,以提高仿真精度。輪軌接觸區內車輪網格尺寸約為13 mm×13 mm×10 mm,鋼軌網格尺寸約為5 mm×5 mm×7 mm。在車輪中心處建立參考點,將該點與車輪-車軸接觸區域的表面耦合,并將一系懸掛力施加到該點上。鋼軌長度為36.252 m,以避免端部固定對計算結果的影響。模型中共有8個WJ-7型扣件系統,其他區域的軌下結構支撐剛度和阻尼采用7×7矩陣型“接地”彈簧和阻尼單元模擬。扣件彈條跟端與鐵墊板的支座接觸,鐵墊板的下表面被固定。在平墊片上表面的耦合點處施加扣件預緊力,將墊片下壓在彈條頂端。受到扣件預緊力的作用,彈條趾端將絕緣塊壓緊在鋼軌上,鋼軌底部被軌下墊板支撐。為了提高仿真計算可行性和運算速度,在扣件系統有限元模型中簡化了螺栓、螺母和鐵墊板的結構,將單個軌下墊板簡化為3×3矩陣型“點對點”彈簧和阻尼單元。車輪與鋼軌、鋼軌與絕緣塊、彈條頂端與平墊片、彈條跟端與鐵墊板、彈條趾端與絕緣塊之間的切向接觸關系為“罰”摩擦公式,法向接觸關系為“硬”接觸。接觸類型為“面-面”接觸,滑移類型為“有限滑移”。該模型的主要參數和材料屬性[20-21]分別如表1和表2所示。

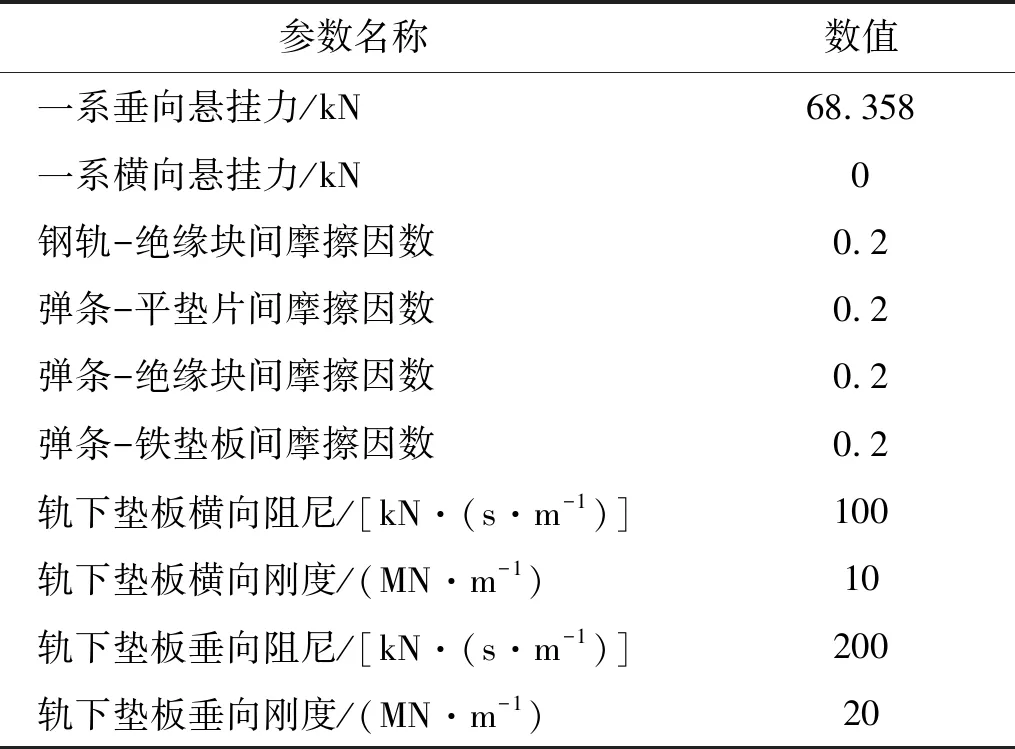
表1 車輪-鋼軌-扣件系統有限元模型主要參數

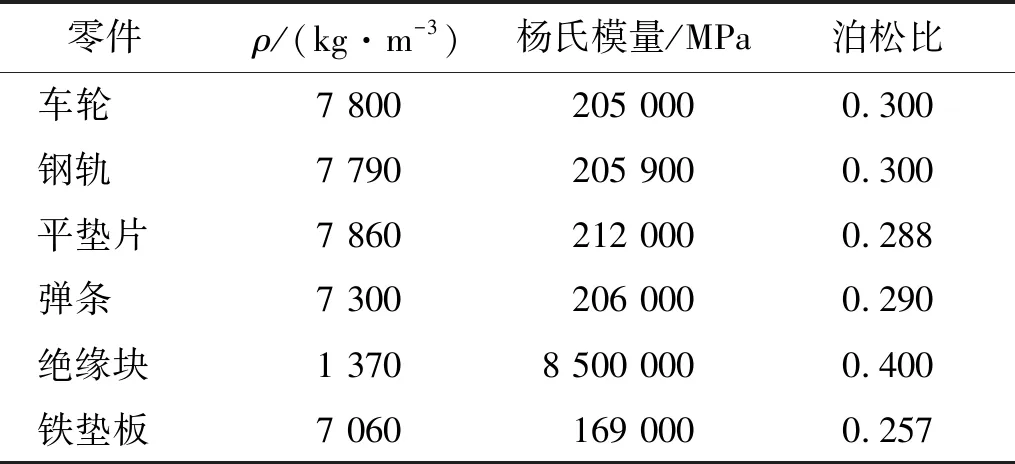
表2 車輪-鋼軌-扣件系統有限元模型材料屬性

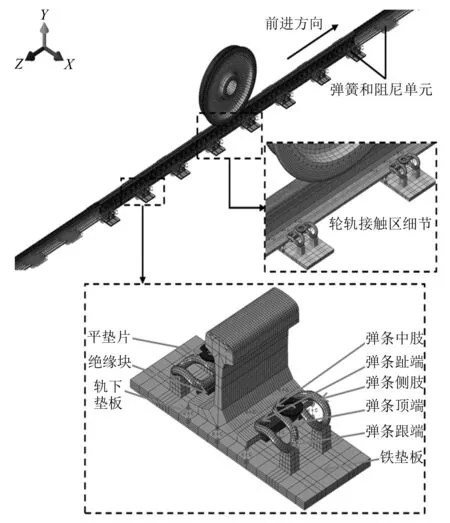
圖1 車輪-鋼軌-扣件系統有限元模型Fig.1 Finite element model of a wheel-rail-fasteners system

1.2 扣件預緊力選取

在扣件彈條振動特性的仿真研究中,扣件系統參數的合理選取十分關鍵。為了選取合適的扣件預緊力,利用車輪-鋼軌-扣件系統有限元模型對扣件系統的受力狀態進行模擬。從扣件系統靜力學分析結果中提取了不同扣件預緊力狀態下扣件扣壓力和中肢位移,并與安裝規范進行對比,如表3所示。當扣件預緊力為26 kN時,扣壓力滿足規范要求,中肢位移與標準范圍相差約8.1%。因此,當選取扣件預緊力為26 kN及以上時,扣件系統模型可以滿足仿真分析需要,仿真中的扣件預緊力取為26 kN。

表3 扣件系統模型驗證Tab.3 Verification of the fastener system model

1.3 摩擦自激振動的復特征值分析法

在ABAQUS軟件中將車輪和鋼軌模型劃分網格,不考慮輪軌摩擦力作用下系統的運動平衡方程[22]為

(1)

式中:M,C,K分別為系統的質量、阻尼、剛度矩陣;x為節點在平衡位置處的位移向量。

在雨雪天氣以及輪軌間存在污染物的情況下,高速列車在上下陡坡區段牽引或制動時,輪軌間的牽引力或制動力可能達到最大黏著力,從而引起輪軌滑動[23]。此時,輪軌間的縱向蠕滑力趨于飽和,其大小約為輪軌間法向接觸力乘以摩擦因數,即

Ff=μKN

(2)

式中:Ff為輪軌間摩擦力;N為輪軌間法向接觸力;μK為動摩擦因數。在仿真中考慮了輪軌摩擦力-相對滑動速度負斜率曲線[24]的影響,假定動摩擦因數的計算公式為

μK=0.2+(0.3-0.2)e-0.011VS

(3)

式中,VS為輪軌間相對滑動速度。

摩擦力作用下輪軌系統簡化后的運動方程由式(1)變為

(4)

式中,MD,CD,KD分別為存在擾動力時系統的質量、阻尼、剛度非對稱矩陣。式(4)對應的特征方程為

(MDλ2+CDλ+KD)φ=0

(5)

式中:λ為特征值;φ為特征向量。根據子空間投影法和QZ法求解該方程,其通解為

(6)

式中:t為時間;αi為特征值實部;ωi為特征值虛部; j為虛部單位。由式(6)可知,當特征值實部大于0時,節點位移隨時間逐漸增大,輪軌系統趨于不穩定。

通常采用等效阻尼比ξ來評價系統穩定性,其定義為

ξ=-2αi/(|ωi|)

(7)

當特征值實部大于0時,等效阻尼比為負數,系統可能產生不穩定振動。并且,特征值實部越大,等效阻尼比越小,對應不穩定振動的發生趨勢越強。

2 計算結果

2.1 輪軌滑動對扣件彈條共振的影響

在頻率范圍0～1 200 Hz內,通過復特征值分析可獲得輪軌間飽和縱向蠕滑力作用下系統摩擦自激振動在頻域內的分布,如圖2(a)所示。由圖2(a)可知,輪軌系統僅存在603 Hz的不穩定振動。潘兵等通過瞬時動態分析獲得了輪軌滾滑接觸工況下鋼軌表面測點處的垂向振動加速度,發現輪軌系統存在約609 Hz的不穩定振動,這與本文采用復特征值分析預測的結果基本一致,在一定程度上驗證了仿真結果的有效性。

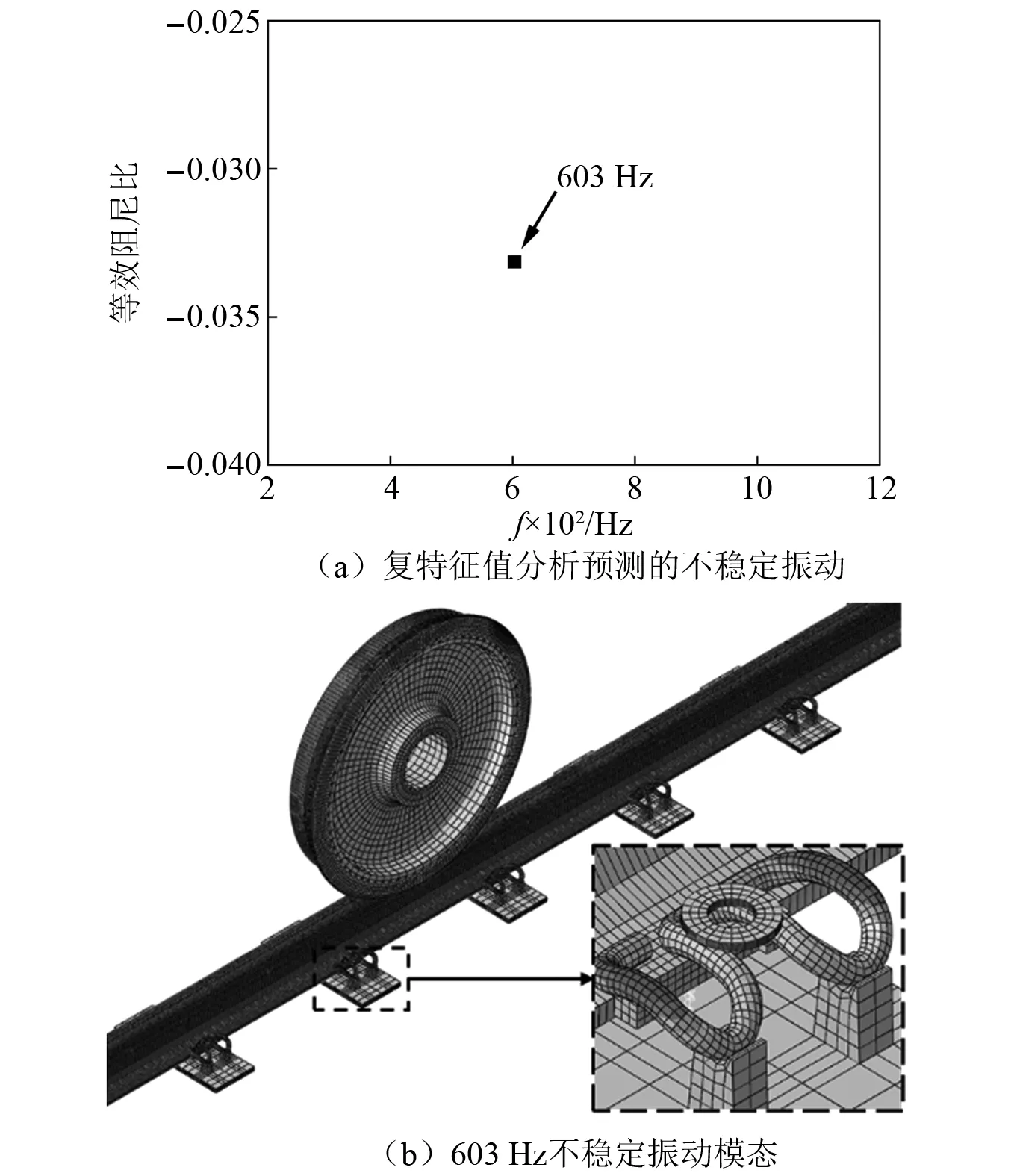
圖2 不穩定振動的分布和模態Fig.2 Distribution and mode shape of unstable vibrations

603 Hz的不穩定振動模態,如圖2(b)所示。從振動模態可以看出,車輪和扣件彈條上均發生了明顯變形,這表明輪軌系統不穩定振動可傳遞到扣件系統中。劉旭鐵的研究模態分析表明,標準安裝狀態下該型扣件彈條在0～1 200 Hz內共有3階模態,頻率分別為570.68 Hz,640.73 Hz和652.78 Hz。其中,彈條第3階模態振型為彈條2個側肢以彈條跟端和趾端為支點,沿軌道方向對稱外翻振動,這與圖2(b)中603 Hz不穩定振動發生時彈條的變形情況相似。并且,該不穩定振動頻率與彈條第3階模態頻率相對誤差約為7.6%,這可能是由于車輪重力和一系垂向懸掛力引起扣件垂向變形,進而引起彈條約束狀態及扣壓力不同于標準安裝狀態,從而導致彈條組裝模態頻率減小。因此,輪軌滑動引起的603 Hz不穩定振動激勵了扣件彈條第3階模態,引起共振,加劇彈條損傷。

2.2 輪軌滑動引起的鋼軌波磨對扣件彈條共振的影響

Cui等指出京廣線高速鐵路某縱坡區段鋼軌波磨的典型波長范圍為130～190 mm,并且,在該區段內部分扣件系統的彈條較新,如圖3所示。這表明部分彈條發生了斷裂失效,從而被重新更換。進一步研究表明,輪軌滑動引起的約607 Hz的不穩定振動是該區段鋼軌波磨形成的原因之一,該振動頻率與本文仿真結果中603 Hz的不穩定振動頻率非常接近。

圖3 鋼軌波磨和較新的扣件彈條Fig.3 Rail corrugation and newer fastener clips

為了進一步研究輪軌滑動引起的鋼軌波磨對扣件彈條振動特性的影響,建立車輪-鋼軌-扣件系統瞬時動態模型。在車輪上施加轉動速度和平移速度,模擬輪軌滾動接觸工況,如圖4所示。為了降低計算量以節省計算時間,動態模型中車輪為剛性體,單元類型為R3D4,鋼軌、扣件彈條等其他模型與圖1所示的有限元模型參數相同。通過重新編譯鋼軌表面節點坐標[25],模擬了鋼軌波磨真實廓形。波磨波長初始值為線路實測典型波磨波長的平均值160 mm,波深H分別取為0.05 mm,0.07 mm,0.09 mm(為了顯示清晰,圖4中波磨的波深為3 mm),波磨廓線方程為

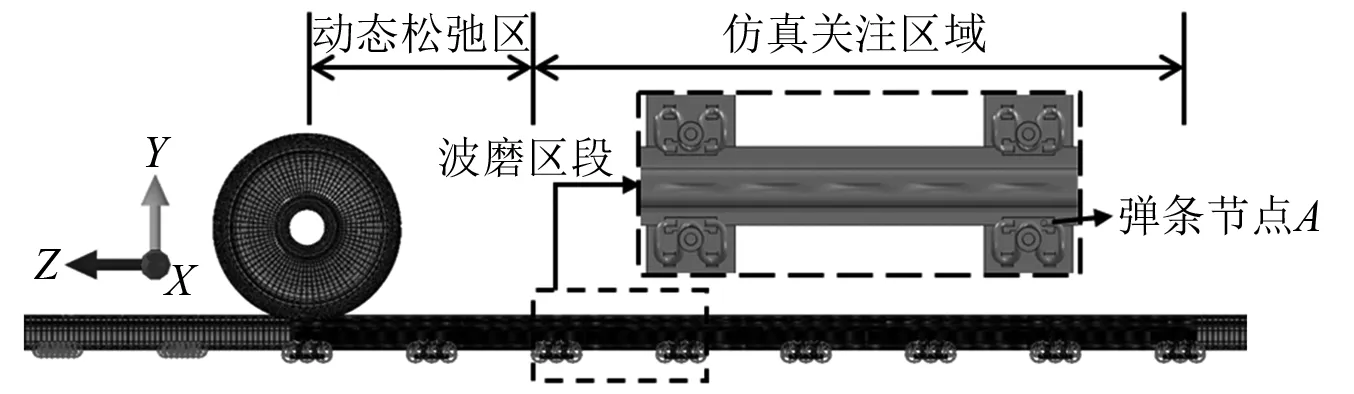
圖4 車輪-鋼軌-扣件系統瞬時動態模型Fig.4 Transient dynamic model of a wheel-rail-fasteners system

y-y0=0.5H{cos[π(z-z0)/80]-1}

(8)

式中:z0,y0為波磨區段鋼軌表面初始節點在ZY平面內的坐標;z,y為其他節點的坐標。車輪以300 km/h的速度在鋼軌上滾動運行4.55 m,波磨區段總長為0.8 m。車輪在運行至波磨區段之前,先經過約1.2 m的動態松弛區,以降低輪軌接觸狀態由靜到動產生激擾的影響。

計算了鋼軌無波磨和存在波磨工況下,仿真關注區域內輪軌間法向接觸力隨時間的變化情況和功率譜密度(power spectral density, PSD)分析結果,如圖5所示。由圖5可知,相比無波磨工況,當車輪通過波磨區段時,輪軌間法向接觸力波動加劇。由輪軌間法向接觸力的PSD分析結果可知,鋼軌波磨激勵輪軌系統產生約521 Hz的振動主頻,并且振動強度隨著波深增加而增大。

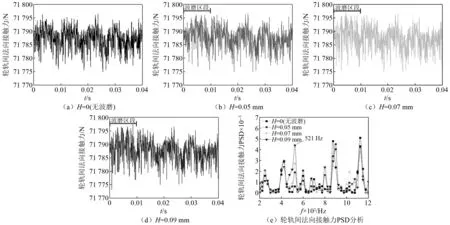
圖5 鋼軌波磨對輪軌間法向接觸力的影響Fig.5 Effect of rail corrugation on wheel-rail normal contact forces

為了研究鋼軌波磨激勵的強迫振動在扣件系統中的傳遞情況,進一步提取圖4中扣件彈條趾端中心節點A的垂向振動加速度,并進行PSD分析,重點關注扣件彈條的前3階模態頻率范圍570～653 Hz的振動情況,如圖6所示。由圖6可知,隨著波磨波深的逐漸增加,彈條節點A在580～640 Hz內的振動幅值不斷增大。這個振動峰值與彈條前3階模態頻率范圍部分重合,可引起彈條共振。因此,當列車通過波磨區段時,即使不發生輪軌滑動,鋼軌波磨激勵的輪軌強迫振動也可引起扣件彈條共振。此外,由于仿真中輪軌接觸狀態由靜態變為動態時會產生初始激擾,雖然設置了動態松弛區,但仍無法完全消除初始激擾引起的振動,導致輪軌法向接觸力(見圖5(e))和扣件彈條節點A(見圖6(e))出現多處顯著的能量聚集,尤其在700 Hz以上的高頻區。因此,當前模型難以準確分析鋼軌波磨是否會激勵彈條更高階模態。在后續的研究中,將對該模型進行改善,降低輪軌接觸狀態變化引起的初始激擾的影響,進一步分析鋼軌波磨對彈條更高階模態的激勵作用。

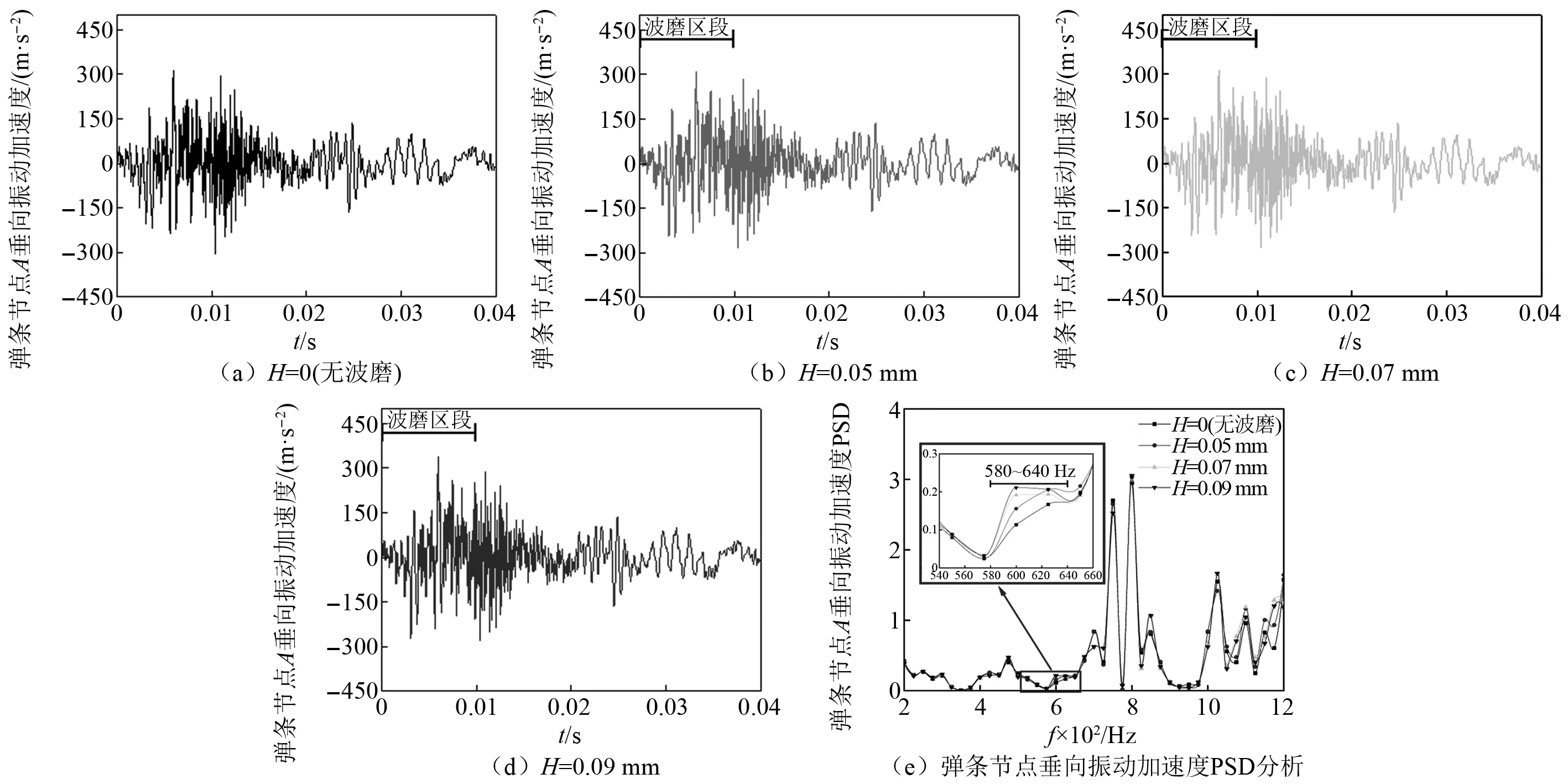
圖6 鋼軌波磨波深對彈條節點A垂向振動加速度的影響Fig.6 Effect of amplitudes ofrail corrugation on vertical vibration acceleration of clip node A

進一步研究不同波長鋼軌波磨對扣件彈條模態的激勵作用,分別計算了波磨波長λ為130 mm和190 mm、波深均為0.09 mm工況下扣件彈條趾端中心節點A的垂向振動加速度PSD分析結果,如圖7所示。由圖7可知,當波磨波長為160 mm和190 mm時,彈條節點在580～640 Hz內均存在峰值,可能引起彈條共振。此外,當波磨波長為130 mm時,彈條節點A在550 Hz頻率處存在峰值。雖然該振動頻率略低于彈條的前3階模態頻率范圍下限570 Hz,但由于行車激勵可導致彈條部分組裝模態頻率減小,因此波長為130 mm的鋼軌波磨激勵的強迫振動也可能引起彈條共振。

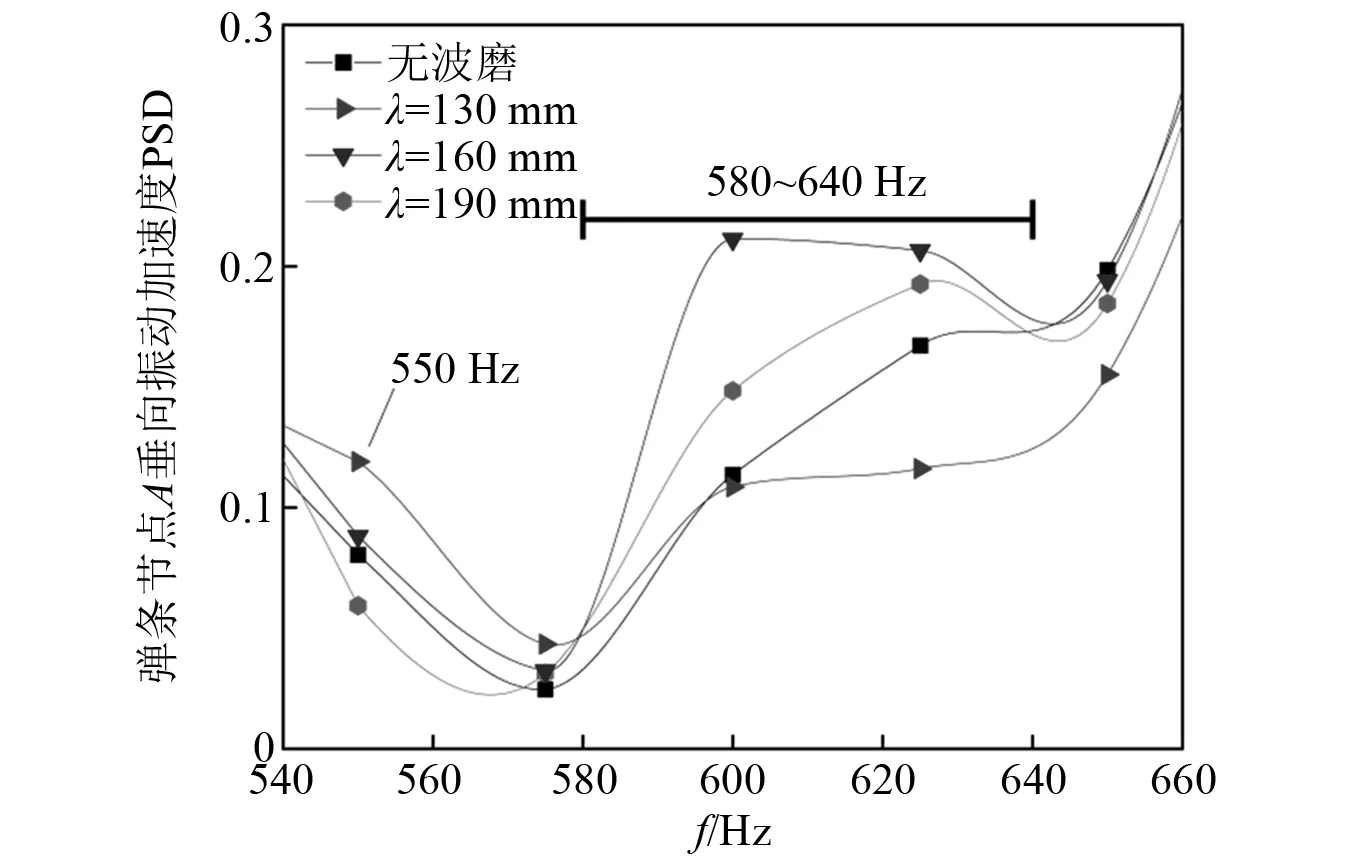
圖7 鋼軌波磨波長對彈條節點A垂向振動加速度的影響Fig.7 Effect of wavelengthsof rail corrugation on vertical vibration acceleration of clip node A

以上分析表明,輪軌飽和縱向蠕滑力引起的603 Hz不穩定振動可通過引發特定波長的鋼軌波磨,激勵與扣件彈條前3階組裝模態頻率接近的輪軌振動,傳遞到扣件系統中,引起彈條共振,加速其失效。

3 影響因素分析

3.1 軌下墊板剛度的影響

在軌下墊板的靜剛度設計值主要是根據軌道部件允許應力和變形確定的,本文仿真模型中采用的扣件系統軌下墊板靜剛度設計值范圍為20～30 MN/m[26]。但由于扣件類型、環境溫度和材料老化等因素的影響,軌下墊板的剛度值在服役期間會發生變化[27]。為了分析不同軌下墊板剛度對扣件彈條共振的影響,計算了輪軌滑動引起的603 Hz不穩定振動對應的等效阻尼比隨軌下墊板剛度的變化情況,軌下墊板剛度范圍為15～35 MN/m,如圖8所示。根據等效阻尼比可以評估輪軌系統摩擦自激振動的發生趨勢,603 Hz不穩定振動對應的等效阻尼比越小,扣件彈條發生共振的可能性越高。由圖8可知,等效阻尼比隨著軌下墊板剛度的增大先減小后增大,但整體變化較小。

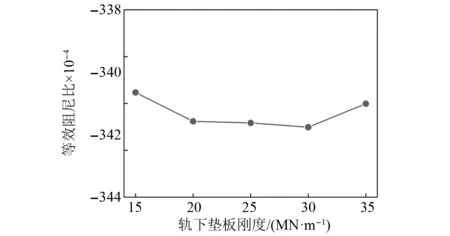
圖8 軌下墊板剛度的影響Fig.8 Effect of stiffness of rail pads

3.2 扣件預緊力的影響

對不同預緊力工況下車輪-鋼軌-扣件系統的穩定性進行分析,重點關注603 Hz不穩定振動的發生趨勢。仿真中扣件預緊力范圍為25～29 kN,該不穩定振動對應的等效阻尼比如圖9所示。由圖9可知,扣件預緊力的變化對等效阻尼比的影響相對較小。

圖9 扣件預緊力的影響Fig.9 Effect of fastener preload

4 結 論

(1) 當輪軌接觸面之間存在污染物,高速列車在上下縱坡區段牽引或制動時,飽和縱向輪軌蠕滑力引起的約603 Hz不穩定振動與扣件彈條第3階模態頻率接近,可引起共振,加速彈條失效。

(2) 輪軌滑動引起的603 Hz不穩定振動可導致高鐵線路縱坡區段鋼軌波磨的形成,當列車以300 km/h的車速通過此區段時,即使輪軌間不發生滑動,鋼軌波磨激勵的輪軌強迫振動也可引起扣件彈條共振。

(3) 軌下墊板靜剛度、扣件預緊力對輪軌滑動引起的603 Hz不穩定振動的發生率整體影響較小。

在未來工作中,將采用線路試驗對結論進行驗證。此外,在下一步工作中,將考慮通過改善扣件彈條結構以改變其固有頻率,從而避免共振的發生。