基于LSSA-XGBOOST改進算法的高體鰤魚類體質量預測模型

俞國燕，左仁意，嚴 俊，羅櫻桐，朱琪珩

(1.南方海洋科學與工程廣東省實驗室，廣東 湛江 524013；2.廣東海洋大學機械與動力工程學院，廣東 湛江 524088)

水產養殖過程中，養殖成本占比最大的是飼料成本[1]。為降低養殖成本，需搭建科學的精準投喂模型，環境、魚群、飼料營養等均是影響模型性能的重要因素[2-3]。在工船養殖模式下，水溫、pH等環境因素趨于平穩，飼料種類在養殖開始時已被確定，但不同生長階段的魚群投喂飼料規格隨著魚體質量變化而有所改變。魚群平均體質量是搭建精準投喂模型的關鍵要素[4]，然而養殖過程中的魚群十分活躍，這給魚群體質量測量帶來巨大的困擾。現有學者憑借圖像處理技術在水下完成了魚的尺寸測量[5]，但如何將獲取到的尺寸信息轉換為體質量信息是亟待解決的關鍵問題，故魚群體態特征及其體質量關系研究不可或缺。

魚群體態特征(體長、體寬)及其與體質量的關系是一種重要的生物差異指標[6-7]，也是魚類研究者們進行生長狀態判斷以及生態系統建模的重要依據[8-9]，還對魚群生長狀態及生物量的判斷有較大的幫助[6]。在關于魚群體態特征(體長、體寬)與體質量關系研究中，相關性系數R2常常被用來驗證模型性能，如Sepa P等[10]研究了在厄瓜多爾海洋水域的4種深海軟骨魚的體長、體質量關系，使用冪指數模型(Y=aXb)完成體長、體質量關系擬合，相關性系數R2達到0.940；Najmudeen T M等[11]為獲取3種遠洋鯊魚體長、體質量關系及其相關系數，在阿拉伯海東南部采集了525組數據完成擬合，相關性系數R2達到0.901；陳鋒等[12]完成察隅河及其支流貢日嘎布弧唇裂腹魚體長、體質量關系對比研究，計算相關系數后確定其體長、體質量關系符合W=2.72×105SL2.888方程，相關性系數R2達到0.972。除使用傳統數學模型的方法描述魚體長-體質量關系外，新的研究方法也層出不窮，如林雅蓉等[13]利用繪圖求積法完成中華哲水虱體長、體質量測定及其關系擬合等。此外，還有大量學者致力于尋求適用性更強、擬合度更高的新型回歸方法，如張志偉等[14]使用神經網絡模型對數據進行回歸，搭建了具有外延性(即預測能力)、擬合性能良好的模型。然而上述擬合方法大多需要大量樣本數據支撐，僅采集數據就需好幾年的連續記錄[11]。

隨著中國深遠海養殖事業的發展，大量企業開始著力構建新型養殖模式[15]，與此同時大量適養于深海的魚類開始出現在公眾視野[16]。高體鰤(Serioladumerili)又名章紅魚，是一種生活在水深20～70 m的海洋魚類，具有較高的食用價值，并且生長速度快、養殖周期短，是一種名貴的經濟魚類[17]。中國從1991年開始高體鰤養殖技術的研究[18]，至今對高體鰤的人工養殖技術研究仍未停止[19-20]。2022年6月，南方海洋科學與工程實驗室為驗證工船養殖高體鰤的可行性，開展了高體鰤養殖實驗。為降低養殖過程的飼料成本，需構建一種適用于工船養殖的精準投喂模型，而平均體質量是搭建精準投喂模型的關鍵要素。通過圖像視頻數據判斷魚體質量，可以大大地降低魚群平均體質量獲取難度，然而視頻圖像僅可獲悉魚群體態特征，因此搭建基于魚群體態特征的魚體質量預測模型十分必要。使用傳統數學模型或神經網絡模型搭建體態特征與體質量關系模型時，其對數據集體量要求較高[21]。因此，本研究采用有別于傳統神經網絡的LSSA-XGBOOST優化樹模型完成體質量預測，在保留了決策提升樹(XGBOOST)算法處理小樣本數據的優良性能前提下，優化了模型結構，使LSSA-XGBOOST模型在僅有少量樣本數據的情況下擁有更高的擬合精度，為搭建精準投喂模型提供重要的支撐。

1 材料與方法

1.1 實驗材料

2022年6月22日，第一批高體鰤苗放入養殖倉，初始平均體質量為90 g。2022年8月25日，養殖周期為64 d，共取314條高體鰤，測量其體長、體寬和體質量數據。在數據采集過程中，分別使用直尺和電子秤進行樣本魚的體長、體寬和體質量測量，并使用棉手套擦去魚表面水分，長度精確到1 mm，體質量精確到1 g。

實驗地點為廣西北海市銀海區福成鎮西村至營盤南部海域的廣西精工深水網箱養殖區。實驗平臺為中國船舶集團廣西公司負責改裝修理的“銀漁養0039”游弋式實驗船(圖1)，該船總長48.3 m，型寬9.5 m，型深2.9 m，設計吃水1.4 m，并配備雙機雙槳。養殖實驗期間，實驗船始終沿養殖區固定航線游弋，從而保證實驗期間循環水系統始終能夠從外界獲取優質海水。

為保證養殖艙內水體質量，艙內四角分別設有進水口，進水流量由艙底電磁流量閥操控，并配備全套水質檢測傳感器。艙底中心位置為出水口，進出水時可將雜質、死魚、殘餌等養殖廢料匯集，再利用出水口渦流的帶動排出艙外。

1.2 數據處理

在實驗過程中，往往會產生小部分異常數據點，這些異常數據點常常會造成整體數據集質量下降，不利于數據可靠性等多種負面影響[22]，也對神經網絡模型訓練造成影響，因此參照文獻[23]對異常點數據進行預處理。

1.2.1 極端學生化偏差(Extreme studentized deviate，ESD)數據降噪方法

在實際水質監測工作中，通常有多個異常數據點，ESD方法將單個異常數據檢測 (Grubbs test)方法擴展，使其能進行多個異常值檢測，為了將Grubbs’ test擴展到k個異常值檢測，需要在數據集中逐步刪除與均值偏離最大的值(最大值或最小值)，同步更新對應的t分布臨界值，檢驗原假設是否成立。算法流程如下：

計算與均值偏離最遠的殘差Rj：

(1)

計算臨界值λj：

(2)

式(2)中：n為數據量；j為預去除的第j個量；tp，n-j-1表示t分布臨界值。

1.2.2 傳統數學模型

1)Gauss曲線

Gauss曲線是一種常用的擬合曲線模型，滿足正態分布的高斯函數如下：

(3)

式(3)中：μ為數學期望；σ2為標準方差。常見應用數學模型擬合魚類體質量與體態特征關系時，大多選擇體長和體質量兩項參數。

2)Logistic曲線

Logistic曲線是一種典型的S型函數，又名Sigmoid函數，常常被用來描述生物量增長狀態，生物數量增長本身應當符合指數型增長，受環境阻力(生存空間、天敵數量等)的影響，在其增長至一定數量后，達到極限數量K值并維持穩定。從整體曲線變化來看，前期爆炸增長及后期環境阻力減緩其增長，使曲線整體呈S型，即增長速率先增大后減小。其數學方程表示為：

(4)

式(4)中：P0為初始狀態；K為終值；參數r用于衡量變化速度。

3)冪函數曲線

冪函數曲線即指數函數，屬于初等函數之一，常用于描述微生物增長狀態，即擁有所有生長所需資源且無環境阻力下的生物量增長形式。方程結構調整如下：

(5)

式(5)中：K、t為常數；F(0)為初始狀態。

目前常用的體長、體質量關系擬合方法為Von Bertalanffy方程[24]：

W=aLb

(6)

式(6)中：W表示體質量；L表示體長；a、b均為實數，可使用SPSS軟件計算得出。

1.2.3 LSSA-XGBOOST擬合模型

1)麻雀搜索算法(Sparrow search algorithm，SSA)及其改進

麻雀搜索算法是東華大學的薛建凱[25]于2020年提出的一種新型群智能尋優算法，在鳥群覓食過程中，優先找尋到食物的個體稱之為發現者，發現者會向其他個體即加入者傳遞信息，而加入者與發現者相互競爭、搶奪資源。麻雀算法按此模式多次群體尋優，最終選出獲得最高適應度個體，即算法得出的最優解。

初始化種群個體可表示為：

(7)

式(7)中：d表示待優化參數量；n為種群數量。

種群適應度為F(X)，形式為個體適應度f(x)組成的N行矩陣：

(8)

發現者位置隨搜尋范圍變化不斷更新，公式如下：

(9)

式(9)中：p為迭代次數；i、j分別表示個體與種群數(Xi，j表示第i個種群第j個個體)；pmax表示最大迭代次數；α為(0，1]區間內的隨機數；R2表示預警值，范圍取[0，1]；ST表示安全值；范圍取[0.5，1.0]；Q為隨機數；L為維度1×d的全1矩陣。

加入者通過觀察發現者位置，并隨之完成位置更新：

(10)

式(10)中：XP是目前發現者所占據的最優位置；Xworst為全局最差位置；A表示所有值隨機為1或-1的1×d矩陣；A+=AT(AAT)-1；i>n/2時，第i個加入者未獲得食物，需重新選擇覓食位置。

警覺者初始位置在群體中隨機產生，其位置表示為：

(11)

式(11)中：Xbest是當前的全局最優解；β為步長控制系數，其特征服從(0，1)間的正態分布；K是區間[-1，1]下的隨機數；fi表示當前個體適應度；fg表示最佳適應度；fw為最差適應度；ε為常數。

(1)混沌優化(LSSA)

麻雀算法(SSA)初始種群產生方法為構成種群數量(pop)×目標參數(dim)的均勻分布的隨機矩陣，這種方法在群體檢索過程中會生成均勻分布在一片區域內的點，如圖2所示。

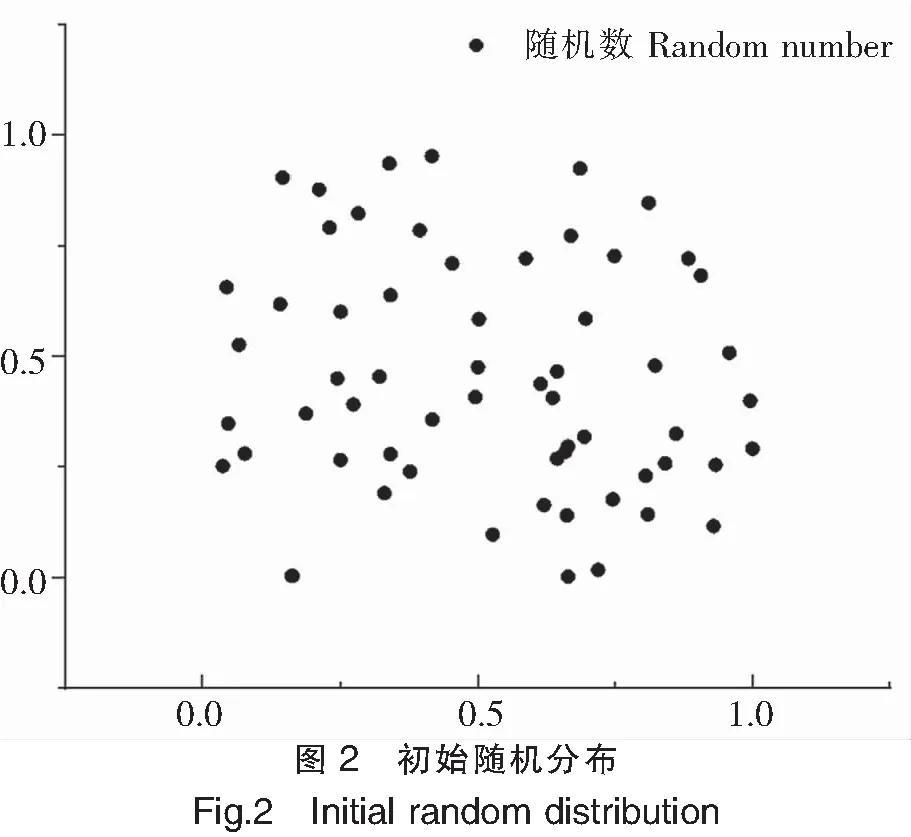
(2)混沌隨機矩陣優化

麻雀算法初始種群優化方法有多種方式，實驗所用混沌隨機數發生器基于Logistic方程，其表現形式為：

X(n+1)=μX(n)[1-X(n)]

(12)

式(12)中：參數u≥3.569 946后，X的值不再發生震蕩，隨后進入混沌狀態。

混沌SSA基于該原理隨機產生的隨機值分布更加分散，如圖3所示。

作為一種群體尋優算法，初始種群分布均勻的程度直接關系到算法的全局搜索能力[26]，對比LSSA初始種群和SSA初始種群在各范圍內的分布直方圖(圖4)可知，LSSA初始種群在[0，1]區間范圍內分布的數量更為平均，這將降低初始化種群時因初始化個體過于集中而漏掉關鍵信息的幾率，提高了算法全局搜索能力。

2)XGBOOST極端梯度提升樹

XGBOOST算法于2014年由Chen T Q等[27]提出，其算法核心在于將多個低準確率分類器組合成一個高準確率模型，針對問題，將對象進行不斷分類判斷并打分，最終某個對象的分數是所有XGBOOST樹評分之和。XGBOOST算法在處理分類和回歸問題中均具有十分良好的表現。

對于XGBOOST而言，其輸出F是由多個評分樹結果相加，表示方法如下：

(13)

式(13)中：F={f(x)=wq(x)}(q：Rm→T，?∈RT)，F表示單個回歸樹空間(CART)，其中q表示樹結構，將訓練集中的單組數據映射到樹結構中。T表示葉結點數量，每個回歸樹空間包含樹結構以及其權重w。除此之外，每個樹節點中都包含有評分，表示為Wi。樹的結構q根據實際案例設定，以常見大小判斷為例：

由圖5可知，若目標是搜尋處于[0，1]的數，樹模型設置了兩層結構，在數據輸入后對其進行打分，觀察圖5(左)，當輸入1.6時，第一次判斷根據其大于1.5直接評分為-1.0，而輸入0.5和1.1時，則分別獲得1.0和0.1的評分。若運算過程涉及多個樹結構，以圖5為例，0.5、1.1和1.6三個數的最終結果由左、右兩側樹各末端評分分別加權求得，若兩側權重相等，則3個數最終評分結果為2.0、0.2和-1.9，可以得出0.5在區間[0，1]內，1.1在區間邊緣，而1.6在搜索區間之外。為了模擬這個運算過程，需用到下述公式：

(14)

在實際運算中，很多關系無法通過簡單累加公式擬合得出，為提高提升樹的漸進能力，方程增加了二次項函數，簡化后的正則公式為：

(15)

樹結構搭建完成后，需對其結構質量進行評估，公式為：

(16)

式(16)中：q為待評估的結構；hi、gi及Ij分別表示損失函數二階、一階統計量、葉節點實例集。

模型在正常運算時，由于葉節點繁多、結構的評估驗證是一層一層循序推進的，單層若有左右兩個節點(表示為IL和IR)，那么該層的損失函數計算將以下列公式表示：

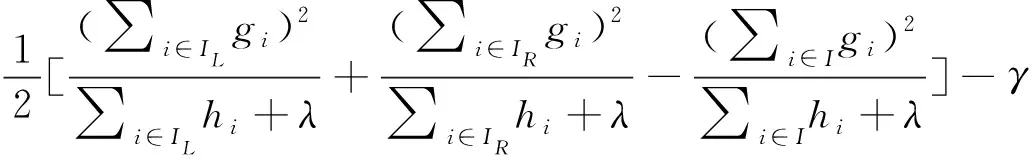
(17)

式(17)中：I表示左右兩個實例集IL、IR的并集。

3)LSSA優化XGBOOST模型

使用決策提升樹(XGBOOST)模型進行高體鰤體態和體質量的預測是一個不斷調整樹模型各節點權值的過程，旨在使樹模型函數持續逼近體態和體質量之間的關系。類似于常規的有監督學習，XGBOOST模型的預測過程需要根據訓練集(體長和體寬數據)預測目標變量(體質量數據)。由于模型無法一次性預測成功，因此每次預測結束后，XGBOOST模型會新增一棵決策樹，根據誤差函數對前一棵樹的預測結果進行調整和糾正，直至最終預測結果達到精度要求。傳統XGBOOST模型最佳樹深度、最佳學習率以及最佳迭代次數等3項超參數由用戶隨機定義，導致模型效果無法保證。為提高XGBOOST擬合精度，使用混沌SSA算法對其3個主要參數進行尋優，獲取最佳樹深度、最佳學習率以及最佳迭代次數(圖6)。

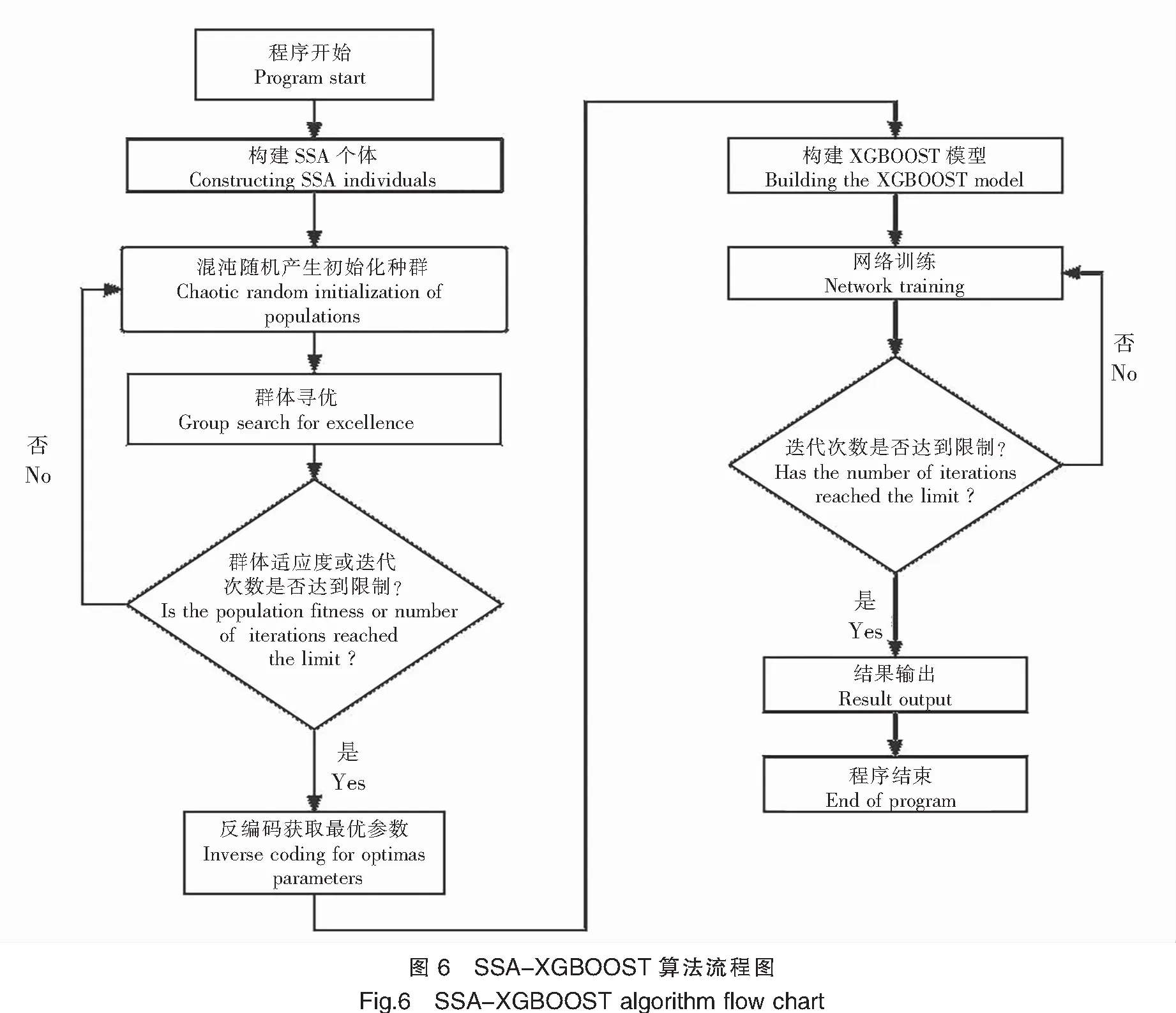
2 模型擬合結果

2.1 ESD數據降噪結果

ESD數據降噪結果如圖7、圖8所示。采用ESD方法識別出5項異常數據，剔除了4個異常數據點(圖中紅色數據點)，有效提高了模型訓練精度。

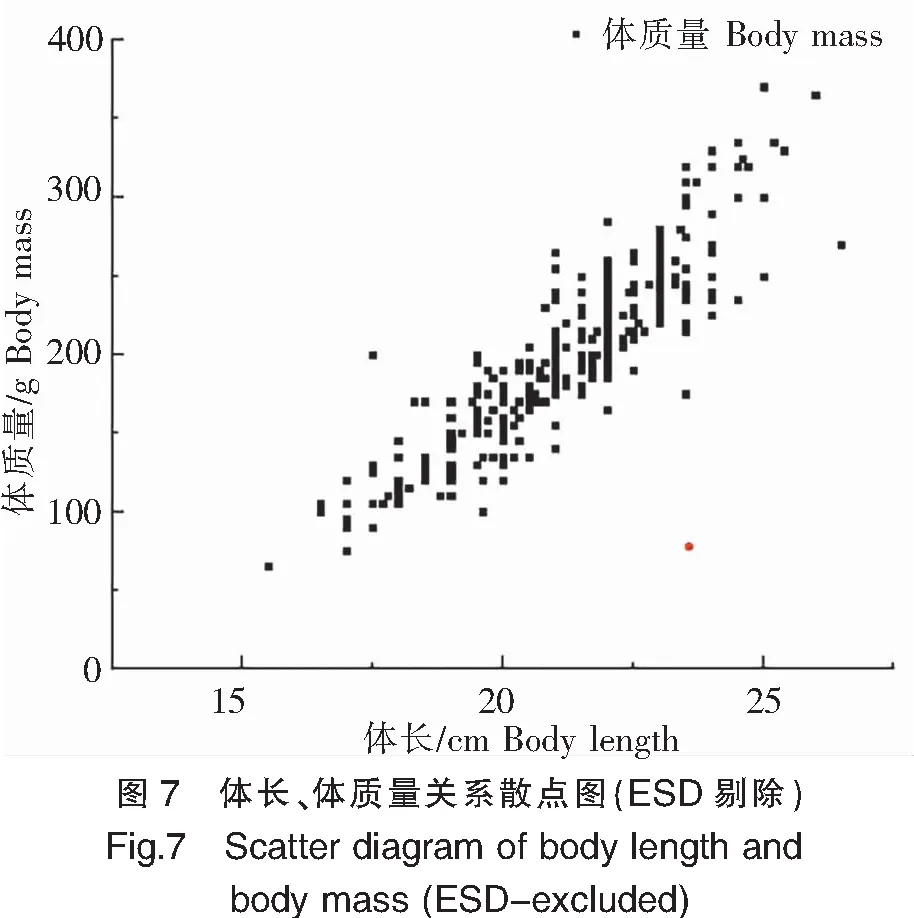
注：紅色點為剔除數據。圖8同此。Notes:The red dot represented excluded data.The same as in figure 8.

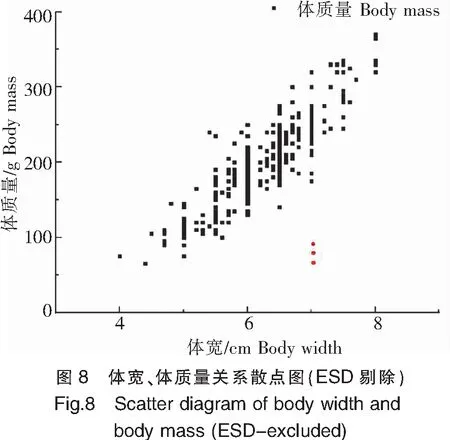
將獲取到的314組數據分別繪制體長-體質量、體寬-體質量散點圖，從散點圖(圖7、圖8)可以看出體長-體質量、體寬-體質量基本呈現正相關關系。樣本魚平均體長為219 mm(標準差σ=2.0 mm)，最大體長為265 mm，最小體長為155 mm；平均體寬為62 mm(σ=0.7 mm)，最大體寬為80 mm，最小體寬40 mm；平均體質量為199 g(σ=59.0 g)，最大體質量為370 g，最小體質量僅60 g。養殖2個月的單條高體鰤平均增重約109 g。

2.2 數學模型擬合結果

2.2.1 常規數學模型擬合結果

1)Gauss曲線

使用Gauss曲線擬合高體鰤體長-體質量關系，擬合效果見圖9，整體數據集呈正相關趨勢，數據點均勻分布在曲線兩側，曲線終點尚未達到峰值，未呈現完整的山峰形Gauss曲線。

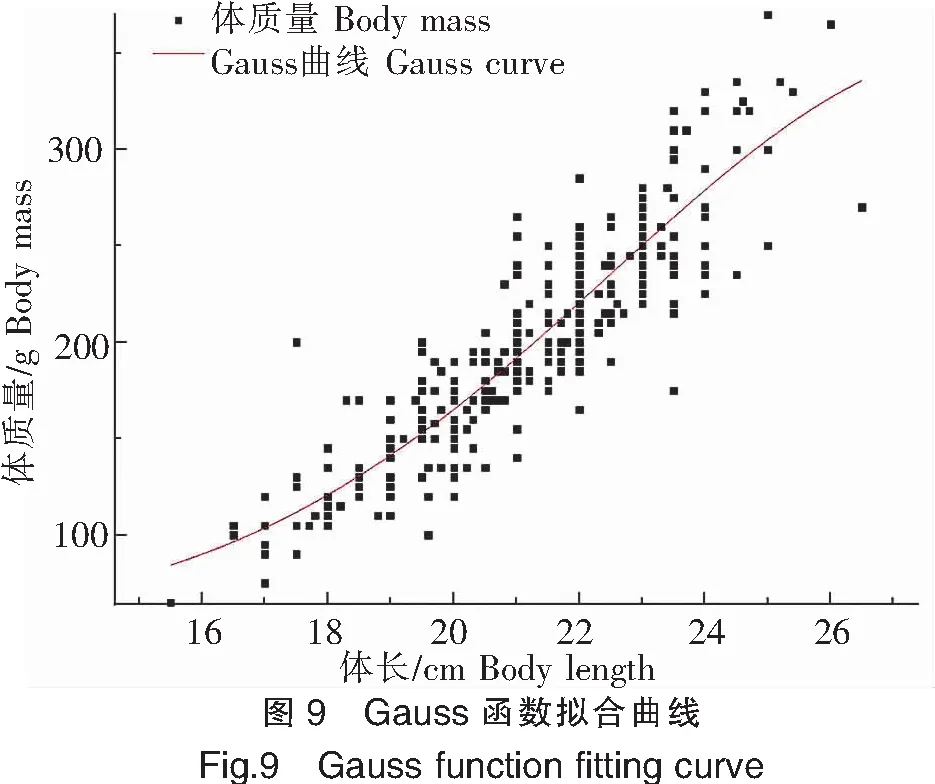
2)Logistic曲線

使用Logistic曲線進行高體鰤的體長、體質量關系擬合，擬合效果見圖10，整體增長較為平穩，增長速率變化不大，未呈現較為明顯的S型曲線。

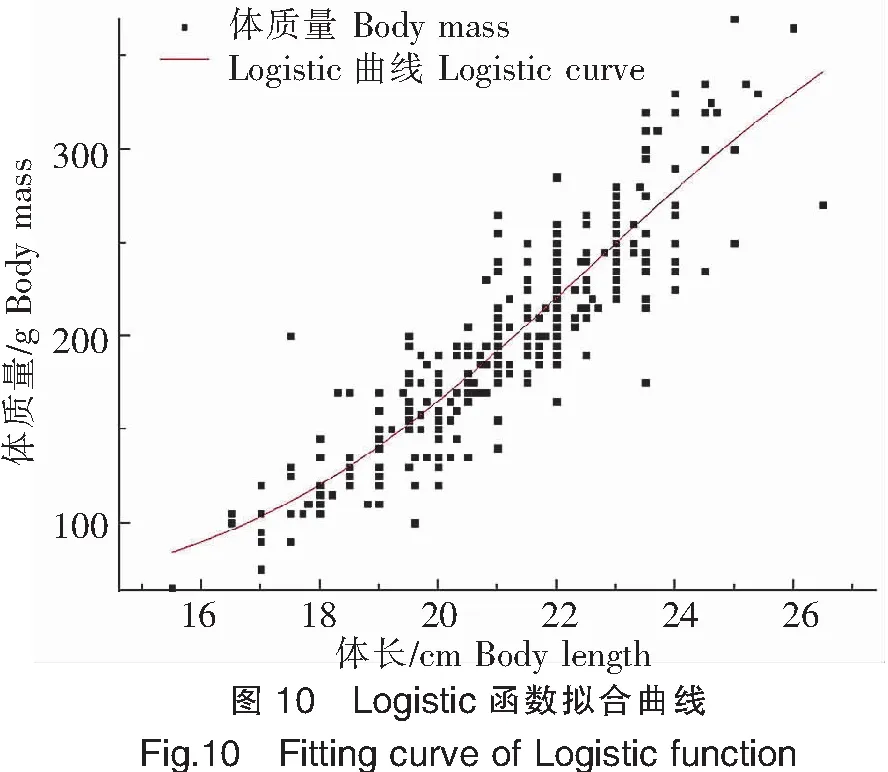
3)冪函數曲線

利用冪函數，選擇體長和體質量兩項因素完成高體鰤體態特征與體質量關系的擬合，擬合曲線見圖11。

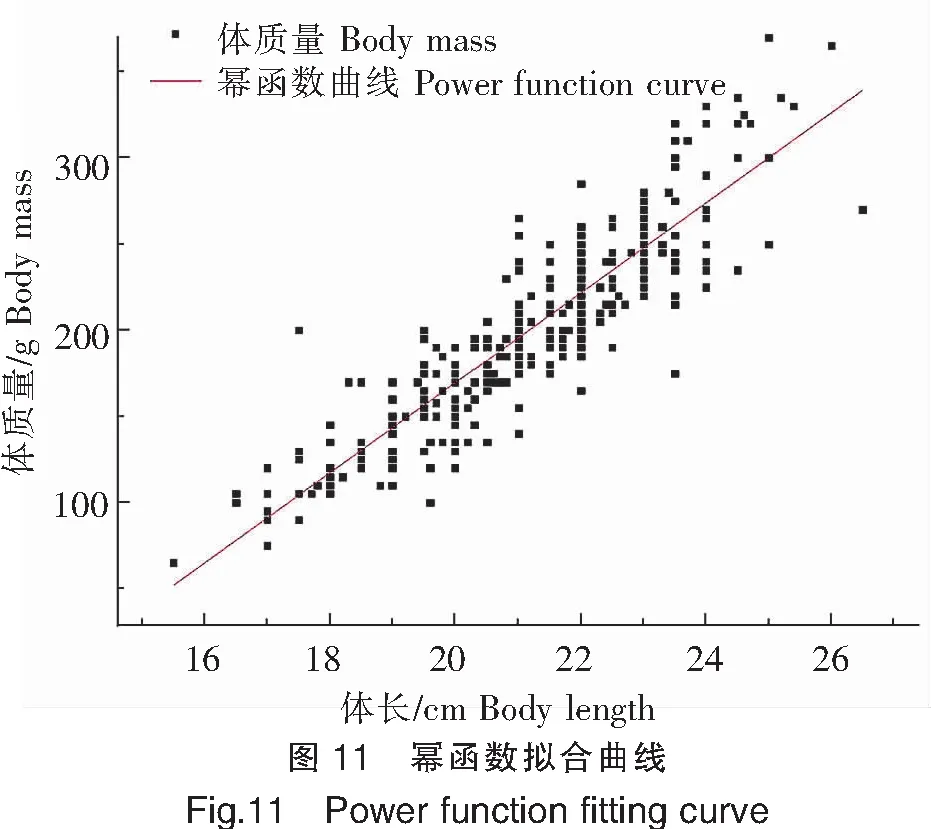
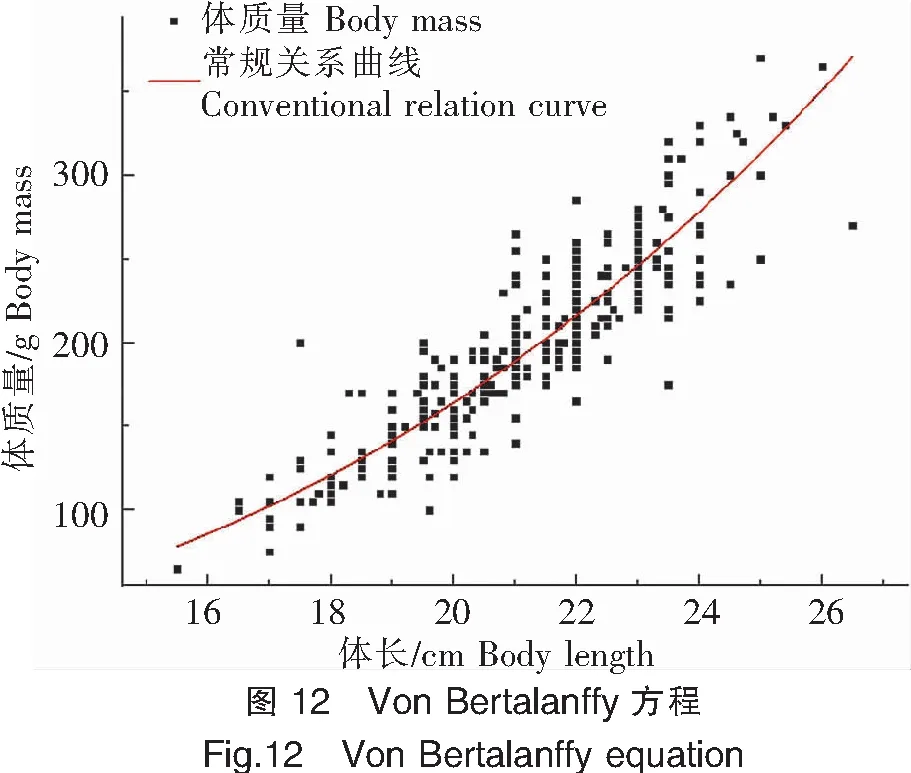
4)Von Bertalanffy方程

Von Bertalanffy方程擬合效果如圖12所示。體長、體質量的關系式為W=0.028L2.896 2，R2=0.771 0。

2.2.2 LSSA-XGBOOST模型擬合結果

開始實驗后，將XGBOOST的3項參數作為待優化量輸入SSA模型，SSA模型參數設置如下：

fun=@getObjValue；%目標函數

dim=3；%優化參數個數

lb=[0.001，0.001，0.01]；

% 優化參數目標下限(最大迭代次數，深度，學習率)

ub=[100，20，1]；

% 優化參數目標上限(最大迭代次數，深度，學習率)

pop=60；%麻雀數量

Max_iteration=10；%最大迭代次數

params.objective=′reg：linear′；

% 回歸函數

種群初始化參數設置如下：

Pop=60；%種群規模

Dim=3；%優化參數個數

Seed=0.5；%起始位置

U=3.8；

%u混沌序列參數，u取[3.569 9，4]

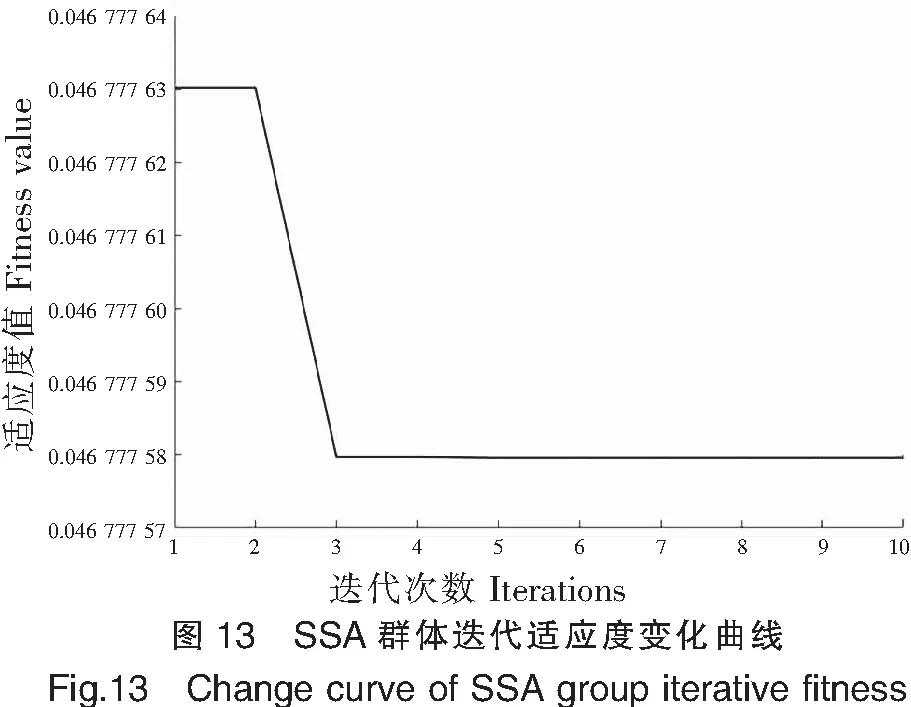
SSA群體適應度隨迭代次數變化曲線如圖13所示，從第三代開始，群體適應不再下降，即種群已達到最佳適應度。

此次實驗以體長、體寬兩項參數為輸入值預測體質量，這是由于在實驗過程中發現使用體長或體寬單一參數輸入預測體質量時，LSSA-XGBOOST模型擬合度分別為0.795 56和0.824 06，僅略高于部分數學模型，而使用雙參數輸入時擬合度有較大提升，擬合度R2達到0.944 16。預測值與真實值的擬合效果對比見圖14，在100個樣本點的擬合跟蹤中表現良好，僅丟失少量目標點。

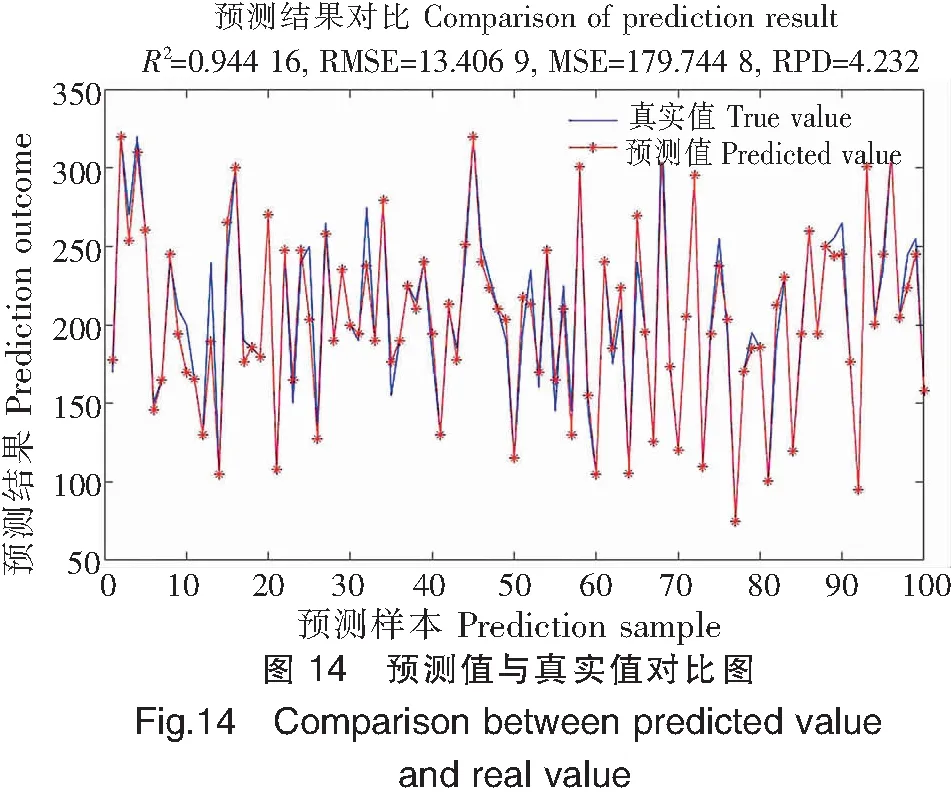
注：RMSE為均方根誤差；MSE為均方誤差；RPD為相對百分比差異。Notes:RMSE is root mean square error；MSE is mean square error；RPD is the relative percentage difference.

3 分析與討論

3.1 與神經網絡模型的對比分析

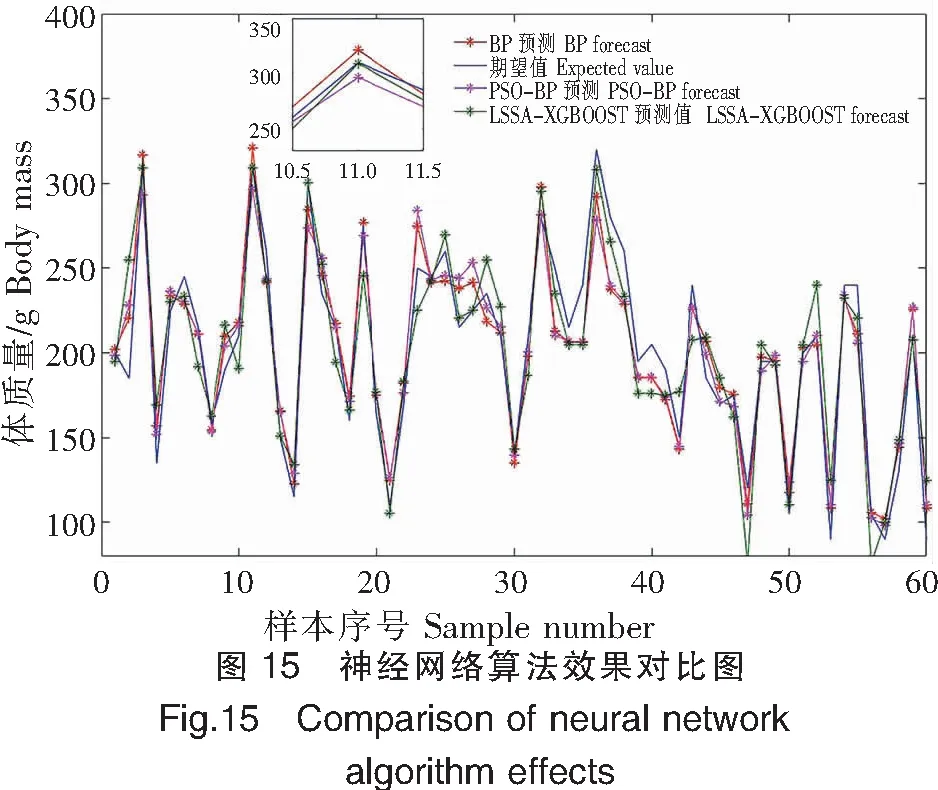
由上述數學模型擬合效果可知，針對此次高體鰤養殖實驗測量數據的常規數學模型擬合并非最優方法。神經網絡模型屬于自適應非線性模型，大量數據表明，人工神經網絡在處理常見回歸擬合問題時有優異表現[28]，除傳統BP神經網絡外，多種優化BP模型如遺傳算法優化BP(GA-BP)、粒子群優化BP(PSO-BP)等都具有處理回歸擬合問題的能力，這些優化算法大多在BP神經網絡初始化時采用尋優算法獲取最佳的權值、閾值等初始參數，從而有效提高BP神經網絡擬合精度。PSO-BP是較為常見的群體尋優算法，在解決回歸預測問題時常常優于GA-BP和傳統BP[29]。本文選用傳統BP神經網絡以及PSO-BP神經網絡與LSSA-XGBOOST算法對比，結果如圖15所示，傳統BP神經網絡擬合度R2為0.877 5，粒子群優化BP為0.910 5，而本文所用LSSA-XGBOOST模型相關性系數R2為0.947 9。以圖15中第11個點擬合效果為例，BP和PSO-BP神經網絡的擬合誤差已經接近其最佳誤差，而LSSA-XGBOOST每棵樹模型的預測都使用shrinkage，削弱其對結果的影響，從而提升整體模型的泛化能力，為后續訓練留出更多的學習空間，有效地防止過擬合。此外，常見神經網絡算法需要大量數據以支撐其算法模型的深度和訓練量，從而提高預測精度，而XGBOOST則不需要太過龐大的數據集，這是由于決策提升樹模型在訓練過程中遵循確定性原則，而確定性原則使其更容易記住簡單的數據變化規律，一旦規律過于復雜，其學習效果便會弱于神經網絡模型。

3.2 總體對比

為使算法擬合效果對比更加直觀，整理上述7種模型擬合度及模型輸入、輸出值，結果如表1所示。常規數學模型僅探討單一參數輸入與輸出關系，故分別以體長、體寬為輸入，擬合體質量關系；神經網絡和改進樹模型則以體長、體寬兩項參數輸入擬合體質量。實驗對比各模型相關性系數R2，結果發現雙參數輸入的神經網絡模型比單一輸入數學模型的R2值更高，其中優化樹模型LSSA-XGBOOST相關性系數最高，達到0.947 9，與BP神經網絡和PSO-BP相比，其平均絕對誤差(Mean absolute error，MAE)、均方誤差(MSE)和均方根誤差(RMSE)都有所降低，具體誤差對比結果見表2。

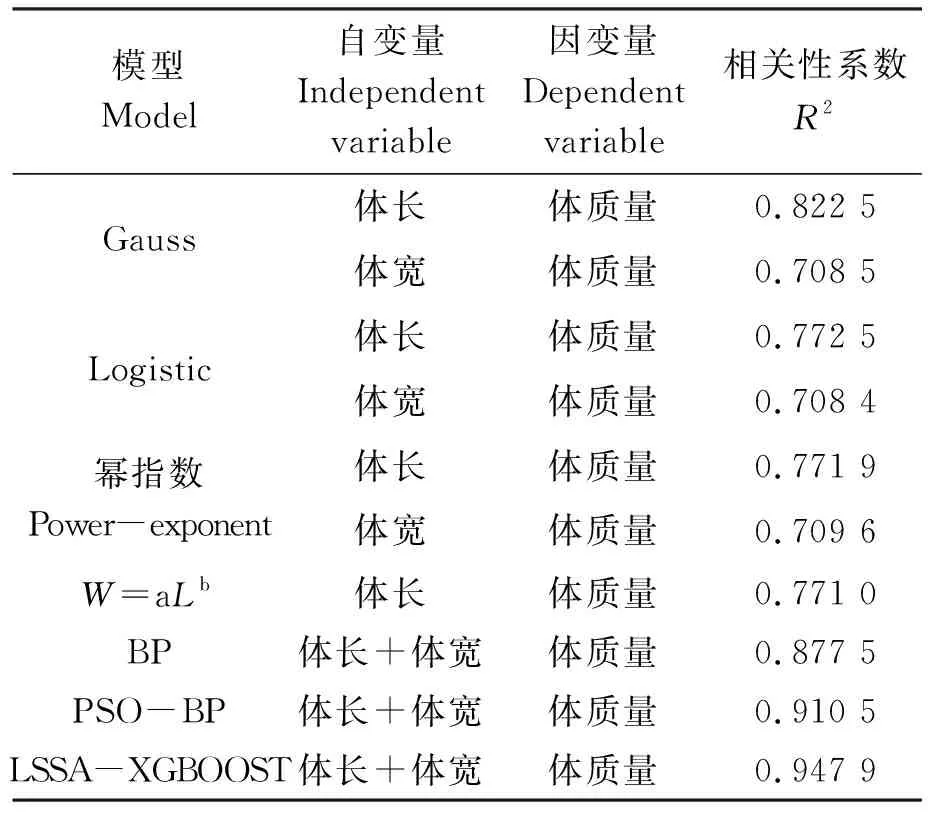
表1 7種擬合模型擬合度R2對比Tab.1 Comparison of fitting degree R2 of 7 fitting models

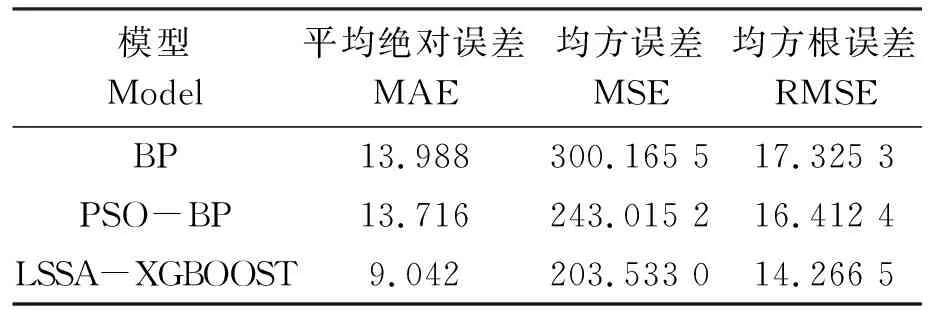
表2 LSSA-XGBOOST模型與神經網絡算法各項誤差對比Tab.2 Comparison of errors between LSSA- XGBOOST model and neural network algorithm

4 結論

1)本文提出的LSSA-XGBOOST模型以決策提升樹模型(XGBOOST)為基礎進行改進，最終使得LSSA-XGBOOST模型在小樣本數據集下有優于其他傳統及改進神經網絡的表現。

2)與常規數學模型擬合相比，LSSA-XGBOOST模型擬合度相關性系數R2(0.947 9)提高了約10%；與傳統BP神經網絡和PSO-BP相比，LSSA-XGBOOST模型相關性系數R2提升約3%，且MAE、MSE和RMSE三項誤差都有明顯降低。在處理小樣本數據集的回歸擬合工作時，LSSA-XGBOOST模型優于傳統數學模型和常規神經網絡模型，能為工船養殖高體鰤精準投喂提供理論依據，后續建議在養殖過程中擴充樣本數據集，并提高混沌隨機數發生器性能，將有效提高高體鰤體質量的預測精度，為飼料投喂、成魚出倉時機判斷及市場預估提供參考。