變形監測網穩定性分析與數據維護的關鍵技術

蘇秀永，胡 航，馬向陽

（1.中國電建集團華東勘測設計研究院有限公司，浙江 杭州 310014；2.浙江華東測繪與工程安全技術有限公司，浙江 杭州 310014）

變形監測網點多布設于變形影響區外穩定位置，有條件的又分基準網和工作基點網，基準網遠離變形影響區，工作基點網則在變形影響區周邊，方便日常變形監測工作開展。然而，受區域地質構造和地球物理環境影響，各監測網點隨時間推移仍會發生不同程度的位移，這些位移使日常變形監測工作產生誤判、甚至誘發安全事故，因此定期復測監測網并進行監測網點穩定性分析與數據維護尤為必要。大量實踐表明，采用全站儀、水準儀和規范的作業方法復測監測網的觀測數據能達到毫米級精度。監測網屬于起算數據不足的自由網，如何正確處理監測網復測數據，自20 世紀60 年代以來一直是國內外測量和形變分析研究的課題。周江文[1]于1980 年提出了擬穩平差，既有明確的測量根據，可為監測網提供前后變化比對的基準面；又沒有強制附和，可保持網形不被扭曲，得到所需的準確信息。歐吉坤[2]等通過分析形變位移場和比較經典平差、偽逆平差，驗證了監測網采用擬穩平差的必要性和優越性。擬穩平差的關鍵是選取符合實際的擬穩點[3]。在監測網點穩定性事先未知的情況下，王海城[4]等利用平均間隙法和t檢驗法對沉降監測基準點穩定性進行了驗證，兩種方法具有一致性；吳杰[5]等針對變形監測網點位異常問題提出了穩定性檢驗方法，并通過實例證明了在平均間隙法的基礎上采用限差法和t 檢驗法對剩余穩定點重新進行穩定性檢驗的必要性；梁麗芳[6]討論了擬穩點選取的兩種方法，并舉例說明了擬穩點法在實際沉降觀測數據處理中的應用。

1 擬穩平差、平均間隙法和限差法

1.1 擬穩平差的原理和性質

以前次平差結果為近似值，結合本次觀測數據進行有特類值的擬穩平差，顧及了監測網點可能不穩定的現狀，變動相對較小的（即相對穩定）點，稱為擬穩點[7]。設X0為擬穩點，X1為變動較大的點，則監測網誤差方程為：

式中，V為改正數；A為誤差方程系數矩陣；為參數估值；l為自由項；n為觀測值個數；t為未知參數個數。

在最小二乘VTPV=min 原則下，由式（1）組成的法方程為：

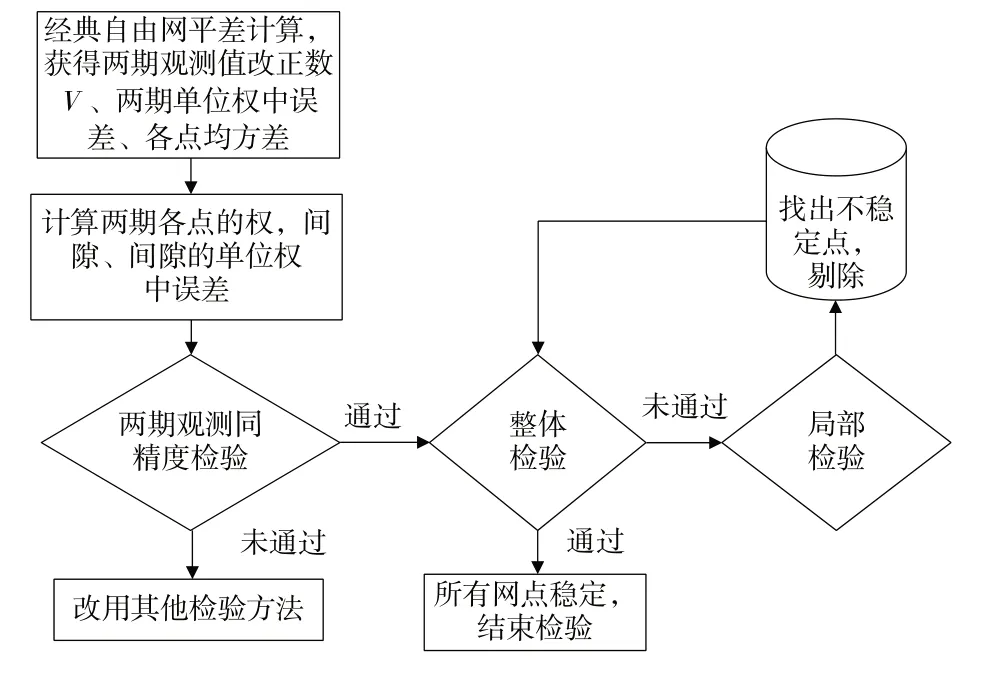
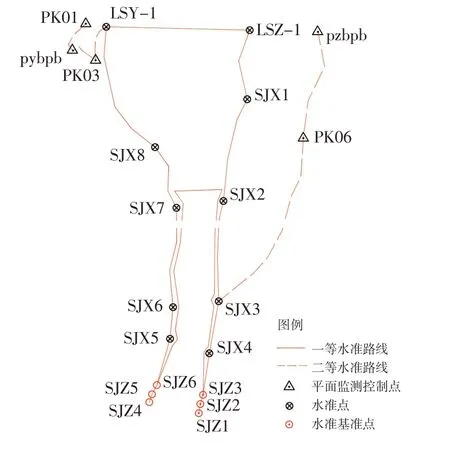
法方程的秩rk(A)=q，q

1.2 平均間隙法

通常兩期復測為同精度，但由于存在觀測誤差，兩期單位權方差估值不相同。在應用平均間隙法前，需進行兩期觀測同精度檢驗。作原假設H0：兩期觀測同精度，構造一個服從F分布的統計量為兩期單位權方差估值；檢驗量F=F(α,f1,f2)，α為顯著水平，f1、f2分別為兩期觀測多余觀測總數。選定α，查F分布分位數表，當P≤F時，接受原假設，否則認為兩期觀測不同精度。兩期觀測精度不同，可用t 檢驗法，限于篇幅，此處不作展開。兩期觀測同精度則采用平均間隙法，分為整體檢驗和局部檢驗，流程見圖1。

圖1 平均間隙法穩定性分析流程圖

根據兩期復測數據，按自由網平差，得到兩期觀測值改正數（殘差），再由改正數計算每期的單位權方差估值[10-11]，則有：

式中，Pd為Qd的廣義逆；fs為獨立的間隙個數。

作原假設H0：兩期觀測期間所有監測網點都是穩定的，則間隙與觀測值改正數均視為正態變量，為同一正態母體方差的無偏估值，構造服從F分布的統計量，其中α為顯著水平，選定α，查F分布分位數表，若F≤F(α,fs,f)，則接受原假設，即所有監測網點都是穩定的；否則表明網中存在不穩定點，需進一步通過局部檢驗，逐點分析找出所有不穩定點。

設檢測網點存在穩定點組F和不穩定點組M，則間隙矩陣和協因數逆矩陣Pd分別為：

采用以下變換，則有：

1.3 限差法

首先以邊長、高差同精度檢測限差為準則，通過兩期實際邊長、高差比較，初步判斷前期起算點的相對穩定性（小于限差的，判斷為穩定）；再對比本期平差坐標、高程與前期坐標、高程計算點位差ΔP、高差ΔH與點位中誤差MP或高程中誤差MH，若，則 為 穩定 點[12]；剔除比值≥2 2 的點，再次擬穩平差，直至所有網點比值<2 2，剩余點即為擬穩點。

2 工程監測網實例

2.1 龍開口水電站變形監測網概況

龍開口水電站位于金沙江中游，壩后式廠房布置在右岸臺地上，總裝機1 800 MW；2012年11月25日下閘蓄水，2013年5月首臺機組發電，2014年1月第5臺機組并網發電。為了對龍開口水電站大壩、左右岸邊坡以及近壩區滑坡體外部進行日常變形監測，左右岸邊坡、大壩壩頂和壩后表面設有若干個位移監測點。左右岸還設有平面變形監測自動化工作基點和后視點，采用極坐標法進行觀測；大壩、左右岸邊坡垂直位移采用水準測量。平面和高程的監測控制網是日常監測工作的基礎，龍開口監測控制網于2012年進行了首期建網，坐標系統、高程基準與勘測設計、施工階段一致；2013 年起逐年對監測控制網進行復測；2015 年對出現位移的PK01、PK07 兩點進行重新選點埋設并重新建網。首期建網、各期復測網精度均達到一等監測控制網精度。一等平面位移監測基準網由PK01～PK08共8個鋼筋混凝土觀測墩組成，網形為邊角網，邊長數為22 條（圖2）。左右岸邊坡表面變形監測兩個自動化工作基點、兩個后視點與PK01～PK06組成工作基點網。一等垂直位移監測控制網由基準點SJZ1～SJZ6，間隙點SJX1～SJX8，工作基點LSdbz-1、LSdby-1，共16個網點組成，水準路線見圖3。

圖2 平面位移監測控制網布置圖

圖3 水準路線示意圖

2.2 監測控制網復測實施

監測控制網的9 次復測均由業主單位分年度招標進行，2013—2015 年度、2016—2018 年度和2019—2021年度由不同中標單位實施。各年度監測控制網復測均采用全站儀、水準儀按照首期建網或上期復測方法，同精度觀測。在外業觀測數據檢查無誤、各項限差符合技術設計書要求后，采用間接平差法進行變形監測控制網嚴密平差計算，并進行粗差探測和分析。

2.2.1 平面位移監測網復測數據處理分析

2012 年首期建網時，以PK08 為固定點、以PK08—PK05 方向為固定方向進行經典平差，選取儀器標稱精度作為先驗中誤差。2013—2015年度平面位移監測網復測，首先對固定點（起算點）PK08、起算方向點PK05進行穩定性分析，即對比PK08、PK05與其他各點邊長與2012年的變化，結果表明各邊變化量均在限差內，初步判定PK08、PK05 基本穩定。以PK08為起算點、以PK08—PK05方向為起算方位，起算數據沿用初期建網成果進行經典平差。以2012年首期建網成果為基準值，比較各年復測的平差成果，計算各期平面位移量；以設計要求的最弱點位中誤差的兩倍（±3.0 mm）為位移量限差，分析可知2015 年復測發現PK03坐標發生順坡向庫區方向顯著位移，2013—2015年的位移量分別為1.0 mm、1.8 mm、3.8 mm，有一定的累積趨勢，在后續觀測中應加強關注，其余各點變量均在限差內，未見顯著位移，建議使用復測成果。

2016—2018年度平面位移監測網復測，首先根據各監測網點所在位置的地質構造，初步判定PK08、PK05 穩定性較好；然后進行兩期觀測同精度檢驗，若精度相同，則采用平均間隙法進行監測網點穩定性分析，若不同，則采用t檢驗法；最后以穩健迭代權法進行監測網點穩定性分析，結果與平均間隙法或t檢驗法基本一致。復測穩定性分析表明，PK08 相對穩定，以PK08 為起算點、以PK08—PK05 方向為起算方位，沿用上一次復測起算數據進行經典平差并提交平差成果，統計各次復測累積平面位移量并形成圖表。

2019—2021年度平面位移監測網復測，首先初步判定PK08、PK05 基本穩定，采用一點一方向經典平差，確認復測網平差后各項指標達到一等邊角網精度要求；再以前次平差結果為近似值，結合本次觀測數據進行有特類值的擬穩平差，得到各點本次平差坐標與點位中誤差；然后根據本次坐標與前次坐標計算兩次點位差與本次點位中誤差的比值ΔP ∕MP，若比值<2 2，則認為該點穩定，否則為動點，剔除動點再次擬穩平差，分析并剔除動點，重復擬穩平差，直至剩余點均滿足比值<2 2，平差結束，將最終擬穩平差結果作為提交成果。由此可知，采用不同的擬穩點進行多次擬穩平差，方向觀測值、距離觀測值個數相同，平差的相對圖形不變；但點位中誤差、平差結果有所不同。2021年復測首次擬穩平差將所有網點作為擬穩點，第二次擬穩平差剔除不穩定點PK06，第三次擬穩平差剔除不穩定點PK02，說明選取合理的擬穩點進行擬穩平差，才能獲取復測基準網點真實可靠的現勢性平面數據。

2.2.2 垂直位移監測網復測數據處理分析

2013—2015年度垂直位移監測網復測，首先檢查位于大壩下游的基準點組SJZ1～SJZ3、SJZ4～SJZ6點間高差，判斷基準點組穩定性較好；再以左岸基準點SJZ1和右岸基準點SJZ6為高程控制網起算點，起算數據沿用初期建網成果，進行附合網平差；然后以2012年首期建網成果為基準值，比較各年復測的平差成果，計算各期垂直位移量；最后以設計要求的最弱點高程中誤差的兩倍（±3.0 mm）為高程變化限差，分析可知基準點未出現明顯沉降，而兩個工作基點LSY-1、LSZ-1和間隙點SJX4～SJX8均出現了明顯沉降，建議以復測成果為準。2016—2018年度垂直位移監測網復測，首先采用平均間隙法和穩健迭代權法檢驗所有垂直位移監測網點的穩定性，兩種方法檢驗結果基本一致，基準點SJZ1～SJZ3 是穩定的；再以SJZ1 為起算點，沿用上一次復測起算數據進行經典平差，提交平差成果；最后統計各次復測累積垂直位移量并形成圖表。2019—2021年度垂直位移監測網復測，首先檢查位于大壩下游的基準點組SJZ1～SJZ3、SJZ4～SJZ6點間高差，遠小于規范限差，判斷基準點組穩定性較好；再以左岸基準點SJZ1為高程控制網起算點，起算數據沿用初期建網成果，進行經典平差；然后與上期成果進行比較，計算兩期垂直位移量ΔH，若大于倍高程中誤差MH，則為不穩定點；最后逐一剔除不穩定點，進行擬穩平差并提交成果。

3 結語

上述工程實例驗證了變形監測網擬穩平差的適用性和優越性，其關鍵是擬穩點的分析和選取。常用方法各具特點，通過實踐分析討論后得出以下結論：

1）平均間隙法是應用統計檢驗理論分析基準點穩定性的有效方法。在實際應用中，有的測量工作者將整體檢驗稱為平均間隙法，將局部檢驗稱為分塊檢驗法或單點檢驗法，本是一個完整的假設檢驗被理解成兩種方法，是不合理的。

2）平均間隙法計算量大，有多次矩陣運算，特別是局部檢驗時，迭代次數多，解算效率偏低。若采用具有自動搜索算法的軟件，該問題能夠得以解決[13]。

3）限差法數學模型容易構造、使用簡便，但判定準則類似經驗公式，有待于結合實際工作進一步研究或與其他方法結合使用。

4）利用監測網點所在的地質構造條件分析其穩定性，屬模糊聚類技術，更適合區域地殼變形監測網的擬穩點選取，因為其需要大量地質、水文和氣象等基礎資料支撐；穩健迭代權法雖然嚴謹可靠，但需進行大量迭代計算，基準轉換復雜，解算效率較低，需要成熟的編程軟件。

5）擬穩點選取得當，以擬穩平差結果為使用成果，能提高監測網靈敏度；通過數據挖掘（作差、作比計算）生成各期間和累計位移量圖、表，數據可比性強。

擬穩平差的合理性是基于多余觀測和控制網中部分點穩定的，工程變形監測網宜先用限差法，再用平均間隙法進行擬穩點分析，互相驗證，確保擬穩點選取正確。需要強調的是，經過分析若控制網中少于兩個穩定點，則無法采用擬穩平差方法。