響堂鋪2號大橋鋼槽梁頂推施工導梁落梁方案分析

王曉磊,劉暢,張鵬,劉煥舉

(1.河北工程大學土木工程學院,邯鄲 056107; 2.中國華冶科工集團有限公司,北京 100176)

當前橋梁的頂推施工中,往往通過鋼導梁和臨時支架等輔助性結構改善主梁在頂推過程中的受力情況[1-2],而導梁落梁是頂推施工的一個重要環節,將直接影響到工程的施工安全與施工進度。導梁落梁方案的科學設計可有效降低主梁結構的最大彎矩值,減輕頂推施工對鋼橋主體結構的不利影響,減少工程事故的發生。因此對步履式頂推施工中導梁落梁方面的研究十分必要。

長期以來橋梁頂推技術的研究備受關注,前人為此做了大量的相關研究。張漣英等[3]考慮了導梁的截面形狀及連接方式,發現導梁變截面點與頂板束錨固點的位置對主梁最大負彎矩峰值影響較小,導-主梁連接束大小對峰值影響較大。張亞麗等[4]針對鋼拱橋頂推復雜的施工環境,提出了一系列步履式頂推的保障措施,有效解決了大懸臂頂推受力復雜、變形大等問題。靳銳勇[5]采用了長導梁法高位頂推技術,并通過工程施工驗證了頂推過程中導梁落梁各階段的施工步驟與技術要求,可為今后工程提供借鑒。高波[6]以某跨線工程為例,通過對比施工方案的科學性,選擇最優方案,從而使得橋梁施工的安全隱患大大降低。時曉曄等[7]通過有限元軟件對導梁結構建立多個模型,對比分析后得出了最優的導梁加固方案,為今后導梁局部的設計提供了理論依據。姜早龍等[8]為了保障大橋的安全施工,利用有限元軟件和現場監測等多種手段驗證了設計方案的可行性,同時表明在結構計算值未達到標準時,可通過對構件的優化,來達到規范的相關要求。

然而,現階段的鋼橋頂推施工中,在非對稱式布置的支架上進行導梁落梁時,仍具有很大的風險,并且相關研究多為空白[9-15],因此對這方面的研究具有重要的現實意義。現采用MIDAS/Civil有限元軟件對響堂鋪大橋步履式頂推施工建立有限元模型,通過對導梁在非對稱式支架上落梁的兩種施工方案進行分析計算,確定最優的導梁落梁方案。

1 工程概況

響堂鋪2號大橋為青蘭高速公路40+62+40 m鋼-混組合箱梁橋,主梁截面鋼槽梁底寬為3.5 m,橫斷面為單箱單室,懸臂長度1 m,橋面板寬16.5 m。鋼槽梁跨越青蘭高速公路。橋梁設計基準期為100年,設計安全級等級為一級,適用環境類別為Ⅱ類,全橋采用整聯步履式頂推施工法,施工立面布置如圖1所示。

圖1 頂推立面布置圖

頂推導梁縱向長35 m,由2片等高度工字形實腹板鋼板主梁組成,兩片主梁之間由鋼管組成的橫向聯系和上、下平面聯系,導梁與鋼槽梁通過焊接方式連接。鋼槽梁和導梁均為Q345鋼材,鋼梁頂推到位后,采用整體落梁的施工方案,頂推施工中臨時支架布置情況見圖2。

圖2 臨時支架平面布置圖

當導梁從臨時支架一頂推到臨時支架四與五時,即導梁頂推至40～94 m并落梁的階段,此時由于臨時支架分布不均勻且頂推距離不斷增加,若繼續頂推,則會使導梁桁架破壞的風險增大,整體頂推系統可能會突發傾覆出現工程事故,阻斷下方高速通行,給車輛和人員帶來安全隱患,故此頂推階段較為危險,選擇出科學合理的落梁方案極有必要。在以往的頂推施工方案中,主梁往往采用一次性頂推到位,并整體落梁的方式,而在大跨度頂推施工中,則采用延長臨時支架的縱向長度,減少導梁懸臂距離的方式[11]。針對響堂鋪2號大橋的特殊情況,故依據經驗并結合現場情況,設計出的方案一與方案二。方案一為頂推時導梁于40、45、49、86、90、94 m處每前進一次便進行一次落梁。方案二為頂推時導梁大部分處于懸臂狀況,僅在支架處進行落梁。通過采用數值模擬手段對提出的兩種方案進行對比分析。

2 頂推數值模型建立

為進一步對兩種方案的合理性進行對比分析,現采用有限元模擬軟件MIDAS/Civil建立橋梁頂推施工的有限元模型。以鋼橋此前進行的頂推施工時導梁懸臂28、35和39 m監測數據為依據,驗證數值模型,從而保證數值模型的真實性與可靠性。

2.1 模型搭建

根據結構設計圖紙,對導梁結構進行劃分后,通過搭建兩工字梁間的桁架結構,建立起導梁的有限元模型。依照鋼槽梁的工藝設計圖和現場梁段的長度和焊接次序,建立出主梁結構單元,最終將主梁與導梁進行剛性連接,從而得出頂推施工的有限元模型,如圖3所示。

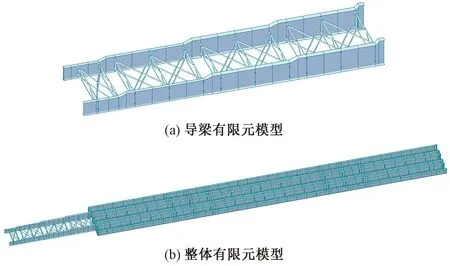
圖3 頂推施工有限元模型

在模型邊界條件的搭建方面,由于實際工程中,主梁是受自重作用而落在臨時支架上的,兩者并無焊接關系,故主梁結構與臨時支架之間采用僅受壓的彈性連接[16-17]。因為頂推施工中每次頂推距離有限,故有限元模型可以簡化為前端懸臂的超靜定連續梁,各步履式千斤頂可以認為與主梁之間為鉸接,主梁后側由鋼架承臺支撐部分的邊界條件可認為是固定端[14]。

在模型分析方法的選取上,參考當前業界針對頂推施工中,利用數值模擬進行分析計算的兩種類型:“倒退算法”和“前進算法”[6,15]。由于“倒退算法”中的節點不發生改變,因此更容易提取和記錄主梁結構應力與撓度的數值,故本文中采取“倒退算法”對頂推施工的有限元模型進行分析和計算。

2.2 數值模型驗證

通過調整邊界條件,建立導梁懸臂距離分別為28、35和39 m的有限元模型,由有限元軟件MIDAS/Civil分別計算出主梁結構的應力與撓度,并將其與實際監測值進行對比,如表1和表2所示。

表1 頂推過程中導梁根部應力值

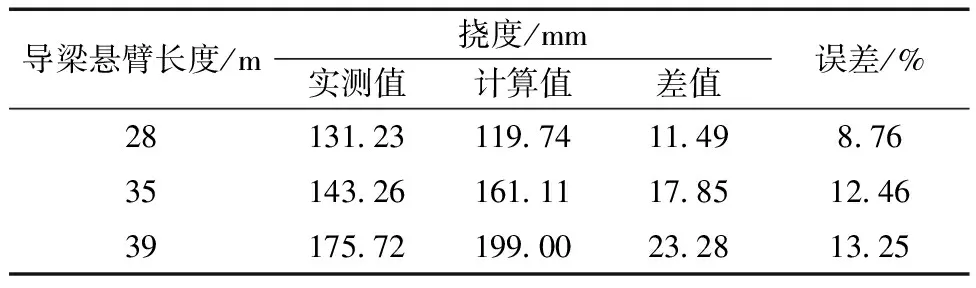
表2 頂推過程中導梁端部撓度值

由表1和表2可知:通過有限元模型分析出的結構應力及撓度值與實際監測數值基本吻合,應力值的誤差分別為10.81%、13.26%、11.28%,撓度值的誤差分別為8.76%、12.46%、13.25%。數據存在誤差主要是兩點原因:①焊接工藝的高溫性和復雜性使主梁結構產生了無法消除的殘余應力。②施工現場長期存在的風荷載。經查閱相關文獻[14]發現誤差值在15%以內,均屬正常情況,而本模型計算的應力值與撓度值的誤差均維持在13.5%以內,因而能夠認定該有限元模型的計算結果應用于實際的橋梁頂推施工中是切實可行的。

在橋梁頂推過程中,主梁的受力隨頂推的進行不斷發生改變,為防止鋼槽梁傾覆,現通過此模型分別模擬兩種施工方案,對比分析導梁與鋼槽梁的穩定性,最終確定頂推的可行性方案。

3 導梁落梁方案對比

3.1 方案一導梁落梁分析

方案一為頂推時導梁于40、45、49、86、90、94 m處每前進一次便進行一次落梁,總共落梁六次,由于兩組非對稱式臨時支架為平行排列,兩組支架間的最大距離達到44 m,主梁結構在兩次落梁中,結構內力變化存在不同,故應對前后兩次主梁落梁進行區分。將40～49 m設定為第一階段,86～94 m設定為第二階段,每階段均獨立建模[18]。通過計算得出的主梁應力及撓度結果如圖4所示。

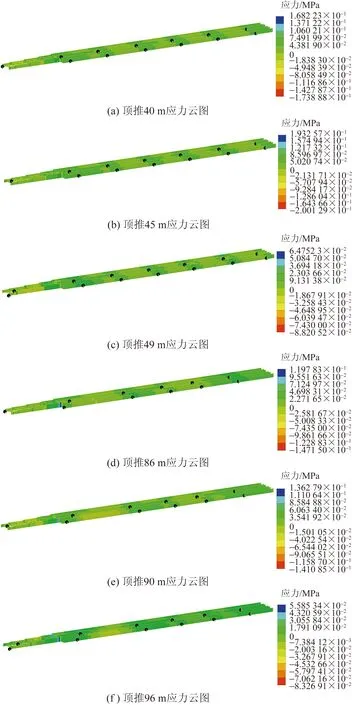
圖4 方案一頂推40～94 m時的主梁應力

由圖4可知,在方案一的第一階段中,最大的應力為200.13 MPa,其出現在頂推至45 m并落梁時,并且應力最大值出現在導梁的多處桁架連接處,受拉與受壓應力交替出現,其內部應力情況比較復雜,且導梁桁架的峰值應力比鋼槽梁的峰值應力大約高116%,在實際的焊接工藝下,此種情況較為危險。而在方案一的第二階段中,結構的峰值應力均控制在了150 MPa以內,最大應力也僅為147.15 MPa,并且最大應力為第二階段的第一次落梁,往后的幾次落梁中,應力值均呈下降的趨勢。有限元模型在各工況下的計算結果見表3。

表3 方案一有限元方法計算結果

在方案一的第一階段頂推施工過程中,鋼槽梁主梁結構支撐位置發生改變,導致其截面的受力狀態不斷變化。導梁部分由于大部分處于懸臂狀態且支撐點不對稱,在重力影響下其應力數值較大且分布不均,相比主梁其他部分的結構應力,其數值高出20%～30%,同時導梁前端在落梁過程中總是有最大撓度值,隨跨度增大而增大。而第二階段與第一階段恰恰相反,在第二階段的非對稱式落梁中,結構應力趨于穩定,無特殊應力出現。

3.2 方案二導梁落梁分析

方案二為導梁頂推過程中不予落梁,僅在第一階段及第二階段的頂推結束時,即49 m與94 m處進行落梁,懸臂長度分別為49 m和45 m,通過有限元模型對導梁懸臂的最不利情況進行模擬計算,從而分析出方案二鋼槽梁的穩定性。圖5為方案二中第一階段的鋼槽梁應力云圖。

圖5 方案二導梁懸臂為49 m時主梁應力及位移

通過計算可知方案二中鋼槽梁的最大應力發生在導梁根部,數值為134.16 MPa,最大撓度為285.16 mm。而第二階段的鋼槽梁的最大應力發生導梁根部的桁架結構,最大拉應力為246.22 MPa,最大壓應力為242.27 MPa,最大撓度為321.72 mm,結果如表4所示。

表4 方案二有限元方法計算結果

3.3 導梁落梁方案對比分析

通過總結上述兩種落梁方案的計算結果,由表5可知方案一的第一階段中,鋼槽梁的結構應力過大,且分布復雜,可能會影響到施工的安全進行。而階段二中,最大應力值卻能均低于150 MPa,應力值反而較階段一減少36%,此階段比上一階段更為安全。在方案二的第一階段中,最大應力僅為134.15 MPa,與方案一相比結構應力最大值降低約33.50%且應力分布均勻[18]。導梁撓度雖為285.17 mm,但由于本工程采用步履式千斤頂等設備進行頂推施工,在整個頂推過程中可通過調整步履式頂推設備向上頂升來抵消鋼槽梁及導梁向下的撓度,故方案二中所增加的導梁末端撓度值可通過頂推設備降低影響。然而由于主梁支座數驟降、跨度增加等原因,使得此方案第二階段應力峰值驟增。相較之下,第二階段中的方案二遠不及方案一安全可靠。

表5 落梁方案計算結果對比

最終經兩種結果對比分析,可知臨時支架采用特殊布置方案時,導梁的落梁方案應采取不同的施工方法,當非對稱的相鄰支架為同側最近時,采用一次性落梁的方案最佳,當相鄰支架為同側較遠時,分布式落梁的方案最佳。因此響堂鋪2號大橋的頂推落梁方案為:第一階段選擇方案二,第二階段選擇方案一。此種方案搭配,有效解決了非對稱式支架布置的情況下導梁落梁的難題,減少了導梁落梁時的安全隱患。而且通過有限元模擬等手段,在積累經驗與數據的同時,也節省了大量的時間成本,有效增加了橋梁施工的經濟效應。圖6為導梁懸臂時現場照片。

圖6 方案二現場施工情況圖

4 現場監測控制

施工監測是施工控制中尤為重要的技術手段[19],在頂推施工的工程中,常常對鋼槽梁的結構應力及形變進行實時監測。在實際頂推過程中將鋼槽梁與步履式頂推配套設備連接節點所在橫截面設為關鍵截面,借助對鋼槽梁應力進行實時監測的科學手段,判斷其結構有無超過材料容許設計值,以達到保障鋼槽梁施工安全的目的。根據有限元軟件計算結果,將鋼槽梁的跨中、四分之一處以及導梁的根部、中部和端部設為關鍵截面,通過安裝應力應變計對其進行現場監測[20],鋼槽梁標準截面應變計布置如圖7所示。

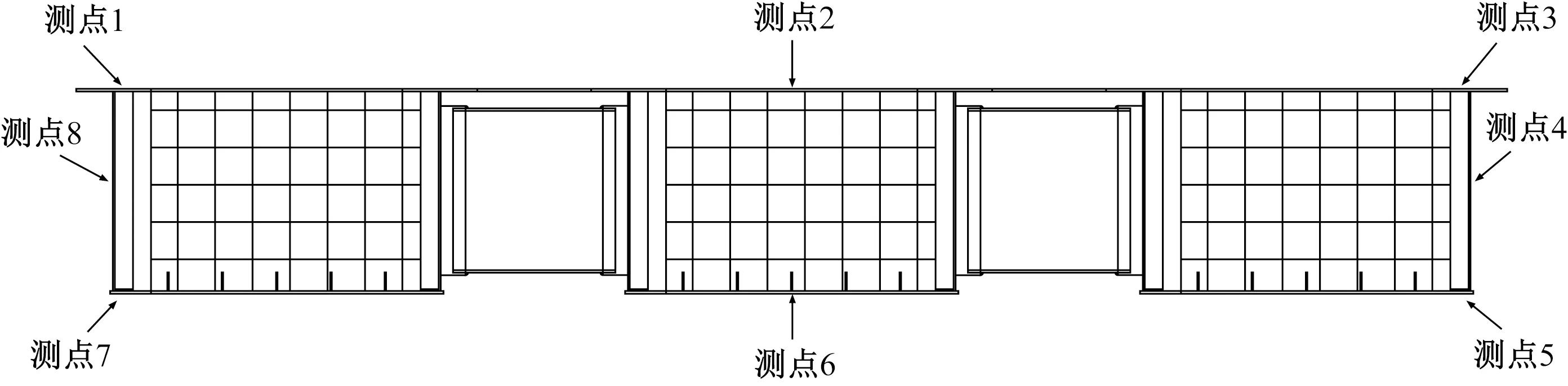
圖7 鋼槽梁標準截面應變計布置

表6給出了在實際頂推過程中各階段的關鍵截面峰值應力實測值與計算值的對比結果。由分析可知:本文所建立的橋梁有限元模型得到的應力數值與現場實際監測值吻合情況良好,最大偏差僅為13.32%,且兩者應力峰值所對應的截面均為導梁根部。

表6 頂推過程關鍵截面峰值應力

分析表6可知,在頂推施工中,頂推長度為86 m時實測值最大,為134.56 MPa,計算值為147.15 MPa,誤差為9.36%。實測值跟計算值大致相同且實測值相對計算值較小,其誤差產生的主要原因是:①焊接工藝的高溫性和復雜性使主梁結構產生了無法消除的殘余應力。②施工現場長期存在的風荷載。

在橋梁頂推施工過程中,鋼槽梁自始至終處于運動狀況,隨著頂推的逐步進行其各截面的撓度也在逐漸發生相應變化,故而對導梁末端的撓度變化進行實時監測同樣是保障臨時支架和主梁安全施工的重要控制手段。表7給出了頂推施工過程中導梁前端到達臨時支架并進行落梁時撓度的實際監測值與有限元模型計算值的數值大小與比較。

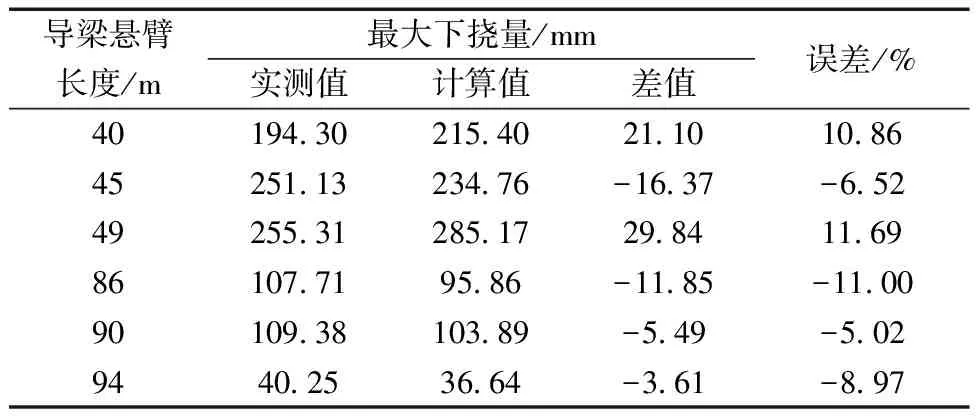
表7 頂推過程中主梁結構的最大下撓量

由表7能夠看出,針對響堂鋪大橋頂推施工所建立的有限元模型在計算導梁前端最大撓度方面具有極為良好的精準性,所得計算值與監測值的誤差均不超過15%。由此可見本模型所得導梁前端撓度數據對實際工程施工是具有一定科學指導意義的。同時本模型用于判斷導梁落梁方案是否可行,也是較為合理的。

5 結論

基于響堂鋪2號大橋的特殊情況,通過分析兩種方案下鋼槽梁的受力特點,結合有限元模型對主梁應力值及下撓量的計算結果,在施工實測數據反復驗證后,得出以下結論。

(1)針對響堂鋪大橋的落梁施工,由兩種方案分階段組合而成的施工落梁方案更為合理,即第一階段采用一次性落梁,第二階段采用分步式落梁的落梁方案。

(2)在橋梁施工中,基于監測數據驗證后的有限元模型,其誤差能控制在15%以內。此種科學的建模方法,有利于得出結構真實的應力狀態和撓度狀態,能有效地對施工方案進行對比設計,提高工程效率,保障施工的安全平順。

(3)通過現場監測與有限元模擬等手段的充分結合,最終使得導梁落梁方案達到最優,結構應力的實測值和理論值均可控制在150 MPa以內,此種分析方法可為今后類似工程提供參考。

(4)在非對稱式支架落梁中,結構峰值應力一般多集中于導梁根部桁架處,頂推時應積極采取實時監測等應力控制措施。