基于元胞傳輸的高速公路收費站站前廣場通行能力模型

易磊,汪凱璇,劉唐志*,緱永濤,劉星良

(1.重慶交通大學交通運輸學院,重慶 400074; 2.寧夏交投高速公路管理有限公司,銀川 750000)

截至2021年底,中國高速公路里程已達16.12萬km,全國已建有收費站10 788個[1],目前的高速公路系統已經較為完善,但是其仍然存在擁堵問題,從整體的擁堵頻率來看,收費站是發生擁堵最頻繁的地區之一。由于重車率過大、車道設置不合理以及交通量突增等問題,部分收費站會產生交通擁堵的現象,限制了高速公路交通系統的運營效率[2]。研究收費站通行能力可以判斷擁堵程度,根據不同車道的擁堵程度采取疏散誘導方法,比如:控制靜態速度[3]、更改收費站車道方向[4]、合理優化車道布設[5]等,以達到緩解交通擁堵的目的。

多數學者通過分析駕駛行為、服務水平、車型比例等影響因素來研究收費站的通行能力。針對駕駛行為影響因素,Saad等[6]建立了一系列基于隨機效應的線性混合模型,以揭示在收費廣場駕駛行為的影響因素。王慧勇[7]基于最小化的收費站運營成本和駕駛員等待成本,建立非線性整數規劃模型。Bari等[8]使用印度收費廣場的數據統計分布分析了服務時間對通行能力的影響。李君羨等[9]將通行能力估計問題轉換為服務時長分布和影響因子兩個方面進行分析,確定了收費車道車輛類型的比例的描述方法。收費站通常都是混合交通流,Navandar等[10-11]提出一種等效系數,將混合交通流等效為小汽車組成的均衡交通流,并在此基礎上研究了收費站的服務水平和通行效率。劉曉倩等[12]使用數學分析法確定了單車道服務時間的分布特性和最大似然估計,從而確定了收費站單車道的通行能力。趙子雪等[13]通過分析混合收費站交通流特性,對收費站的服務水平進行定量劃分,確定不同類型收費站的服務水平標準和相應的最大交通量。Mahdi等[14]研究重型車輛的百分比對收費廣場隊列長度性能的影響,結果表明,重型車輛在交通流量中的百分比顯著影響了收費廣場的隊列長度。這些研究方法大多數是從不同影響因素的角度來分析收費站的通行能力,變道、加減速的駕駛行為會增加交通事故風險,服務時間過長、電子不停車收費系統(electronic toll collection,ETC)設備識別錯誤可能會導致交通擁堵,半自動車道收費系統(manual toll collection,MTC)車輛過多、重車率過大的車型比例同樣會直接影響到通行效率,這些影響因素可以在一定程度上反映通行效率的高低,但是想要得到通行能力的顯式值還需要進一步地研究。

現有研究中,計算收費站通行能力的模型主要有兩種類型:分析模型和仿真模型。分析模型大都是基于交通流理論而建立的,更加具有邏輯性和適用性,但是計算過程通常很復雜[15]。基于車輛種類、收費口車道配置等因素,Zarrillo等[16]構建了站前廣場通行能力計算模型。趙述捷[17]將MTC與ETC進行了比較,提出了計算和分析計重收費通道通行能力的新模型。Yong等[18]通過建立一個平衡模型和兩個數學規劃模型,研究了收費廣場的設計通行能力。Yu等[19]開發了一種基于仿真的整數規劃模型,提供更高效的收費廣場運營方案。Qian等[20]在傳統NS(Nagel-Schreckenberg)模式的基礎上,建立了一種改進的元胞自動機模型,用于分析混合式收費站的交通流。Kim等[21]通過觀測收費站的實時交通流量和車輛行程時間,建立模型分析收費廣場的通行能力。利用微觀仿真軟件來建立模型更加方便和直觀,但是具有一定的隨機性,存在精度不足的缺點[22]。研究中常用的微觀仿真軟件是德國PTV(Planungsbiiro Transport und Verkehr)公司開發的Vissim軟件,Dong等[23]在Vissim中設計了五種常規收費站交通場景,用于不同引導策略之間的通行能力比較分析,結果表明收費通道前的引導優于收費廣場后引導措施。Bains等[24]在Vissim中開發了一個經過良好校準和驗證的收費廣場模擬模型,并對幾個場景進行了模擬,以測試其在提高通行能力方面的功效。Beki[25]將強化學習和遺傳算法聯系起來研究收費廣場的通行能力,并使用Paramics仿真軟件開發的模擬收費廣場進行實驗分析。現有研究大多數都是通過模型來計算收費站通行能力值[26],仿真模型可以簡單且直觀地處理多種交通場景,但是不夠準確,理論分析模型雖然計算復雜,但是具有較高的精確度。綜合考慮兩種模型的優缺點,現采用理論分析與仿真相結合的方法來計算通行能力值,以此達到更好的效果。

基于現有研究尚未給出確定顯式值的方法,且沒有把仿真模擬、理論建模與實際檢驗相結合的現狀,通過元胞傳輸思想,把站前廣場等效為規則的幾何區域,簡化計算過程,建立了站前廣場通行能力模型。利用多個收費站的實測數據對關鍵參數進行標定,采用VISSIM仿真軟件驗證模型的準確性。研究在不同的長度、不同車道數目以及不同車道配置下站前廣場的通行能力,不僅對判斷擁堵程度提供理論依據,還對提升運營效率有一定的參考。

1 模型建立

由于收費站站前廣場的車道數由少變多,是一個不規則過渡區域,導致每個不同截面的通行能力存在差異。元胞傳輸模型可以將站前廣場劃分為規則區域,通過每個元胞的車輛數變化來描述整個區域的交通流變化,簡化通行能力的計算過程。為了提高收費站站前廣場通行能力的計算精度,減少誤差,為收費站擁堵問題的緩解提供理論支持,綜合考慮常見的通行能力計算方法的優缺點和站前廣場的實際情況,擬建立基于元胞的通行能力模型來分析收費站站前廣場的通行能力。

1.1 站前廣場規則化

Daganzo[27]在經典的宏觀交通流模型LWR(Lighthill-Whitham-Richards)模型的基礎上提出了元胞傳輸模型(cell-transmission model,CTM),該模型結合流體力學理論,將道路劃分為一個個相連的元胞,根據元胞間的交通流傳輸關系描述路段交通流狀態。Laval等[28]在元胞傳輸模型的基礎上,增加換道行為,建立了LC(lane changing)模型,該模型很好地再現了排隊中不穩定的緩慢增長現象,并且具有較好的短時預測交通流動態效果。元胞傳輸模型多應用于高速公路和專用車道的研究以及交通仿真,尚未在收費站中得到應用。現基于元胞傳輸模型的原理,將收費站的站前廣場分為長度相同的n個元胞,以此將畸變區域等效為規則的幾何區域,這樣可以更直接、更簡單、更準確地計算此區域的通行能力,如圖1所示。元胞傳輸的原理表達式為

圖1 站前廣場規則化

qi-1,out=qi,in

(1)

qi,out=qi+1,in

(2)

式中:qi,in為單位時間內元胞i流入的車輛數,輛;qi,out為單位時間內元胞i流出的車輛數,輛。

車輛行駛過程中會連續地從一個元胞駛向下一個元胞,直到駛出最后一個元胞為止。由于交通流是一個連續的過程,上一個元胞的駛出車輛數與下一個元胞的駛入車輛數相等,單個元胞的最大駛入車輛數與單位時間內初始元胞的最大駛入車輛數相關。基于元胞傳輸模型的原理,將站前廣場規則化,通過計算車道內所有元胞的通行能力得到單車道通行能力,而多條車道之間會存在變道行為,不能簡單地將單車道通行能力簡單相加,因此需要引入車道折減系數,就可以計算整個站前廣場的通行能力。

1.2 單車道通行能力

整條車道的通行能力是這條路段在一定時間內所能通過的最大車輛數,由元胞傳輸的特性可以知道,單車道的通行能力就是在一定時間內從初始元胞駛入,末端元胞駛出的過程中,所有元胞通過車輛的最大數。所以先對單個元胞的車輛行駛狀態進行分析,得到單個元胞的最大車輛通過數,再利用車道中所有元胞計算單車道的通行能力。在Δt時間內離開元胞的最多車輛數只與單位時間內車輛通過的距離和兩車之間的間距相關。假設t0時刻第一輛車剛駛入元胞i,經過單位時間Δt后,t時刻第一輛車已經駛出元胞i一定距離。為了保證模型的有效性,避免元胞過長不能及時計算車輛數,因此將元胞長度設置為較短的長度,使得在單位時間內車輛通過的距離至少為一個元胞長度,如圖2所示。

為單位時間內車輛通過的距離,為平均車頭間距,m;l為元胞長度,m

單個元胞的通行能力為單個元胞在單位時間內可以通過的最大車輛數,其通行能力與元胞長度、車輛行駛速度和單位時間長短有關。為了簡化分析,將所有車輛看成一個點,長度忽略不計,只考慮車頭間距。單位時間內車輛通過的距離計算公式為

(3)

假設單位時間內車輛通行距離大于元胞長度,即

(4)

則單位時間內單個元胞能通過的車輛數計算公式為

(5)

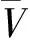
計算t時間內單個元胞最多離開的車輛數,再利用單車道的元胞數進行計算,可以得到單車道的通行能力,計算公式為

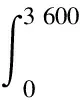
(6)

(7)

(8)

式中:C0為1 h內單個元胞最多離開的車輛數,veh/h;β為該路段元胞數量,個;L為車道長度,m;l為元胞長度,m;Cd為單車道的通行能力,veh/h。

1.3 站前廣場通行能力

多個車道的通行能力不是所有單車道通行能力之和,這是因為不同的車道位置布局在一定程度會產生折減。站前廣場車道數多,各個車道的位置不同,但匝道車道數少,大部分的車輛都需要變更車道才能到達目標收費站。由于變更車道的過程會在一定程度上影響車流狀態,通行能力會存在一定的折減,因此引入通行能力折減系數。ETC或MTC車道若與收費站入口車道直接相對的,車輛不需要進行變道,通行能力折減系數設置為1,即通行能力不折減[29]。在其他位置的車道,通過單個車道的交通量與正對車道的交通量的比例,可以對其他路段的通行能力折減系數進行計算,具體代換過程可表示為

(9)

式(9)中:fn為第n條車道的折減系數,車道從正對主線向外側偏移的編號依次為1,2,…,n;Qn為通過第n條車道的車輛數,輛。

目前,中國高速公路收費站主要采用ETC/MTC混合車道和ETC專用車道。ETC/MTC混合車道的設計必須符合更高的設計規范,以滿足ETC和大型汽車的需求。如果混合車道僅供ETC車輛使用,則該混合車道的通行能力等于單個ETC車道的通行能力;車道在僅供MTC車輛使用的情況下,混合車道的通行能力和單個MTC車道的通行能力相同;車道同時為兩種車輛服務時,MTC車輛的占比越少,其通行能力就越大。在混合交通流中,MTC車輛所占比重越大,ETC車輛對通行能力的影響越小,其衰減速率也就越慢。

ETC/MTC混合車道的通行能力隨混合交通流中MTC車輛比例的增加而降低,降低的速率從0開始逐漸增大,到一定程度后再逐漸減小。利用余弦函數對其變化過程進行了近似表達[30],得出了混合車道的通行能力公式為

(10)

式(10)中:CE為ETC車道通行能力,veh/h;CM為MTC車道通行能力,veh/h;Ch為混合車道通行能力,veh/h;?為混合車道中MTC車輛所占比例。

所以,站前廣場多車道通行能力可以表示為

(11)

式(11)中:m為MTC車道數,條;k為ETC車道數,條;p為混合車道數,條;fj為第j條車道的折減系數;C為站前廣場通行能力,veh/h。

這個模型是將站前廣場整個不規則區域劃分成多個規則的元胞,利用元胞計算單車道通行能力,考慮到不同車道間的變道行為,再引入車道通行能力折減系數,將每條車道的通行能力折減后,最后得到站前廣場的通行能力。相較于其他模型,該模型是基于收費站區域的幾何形狀建立的,可以更好地反映收費站的交通特性,利用元胞傳輸簡化了建模過程,在保證準確性的前提下使計算更加簡單。

2 模型驗證及誤差分析

由于模型中的部分參數無法直接得到,因此通過調查寧夏回族自治區的六盤山收費站、賀蘭收費站、銀川南收費站、北京東路收費站、銀川東收費站、吳忠收費站這六個收費站監控視頻,依托寧夏交投高速公路路網實時監控平臺,結合DSS cloud監控軟件,利用2022年7月4—8日的監控錄制視頻,統計不同車道的交通量、車輛的平均行駛速度和時間,利用大量的實測數據標定模型的關鍵參數。標定參數后對站前廣場通行能力模型進行驗證,為了驗證多場景下的模型準確性,使用VISSIM仿真軟件建立不同站前廣場長度、不同車道數的收費站場景,設置對應的參數進行仿真得到通行能力的仿真值,驗證模型并進行誤差分析。

2.1 參數標定

高速公路收費站站前廣場通行能力計算模型包含的參數如表1所示,其中平均車速、平均行程時間和車道通行能力折減系數三個參數需要根據收費站實際運行狀況調查獲得。

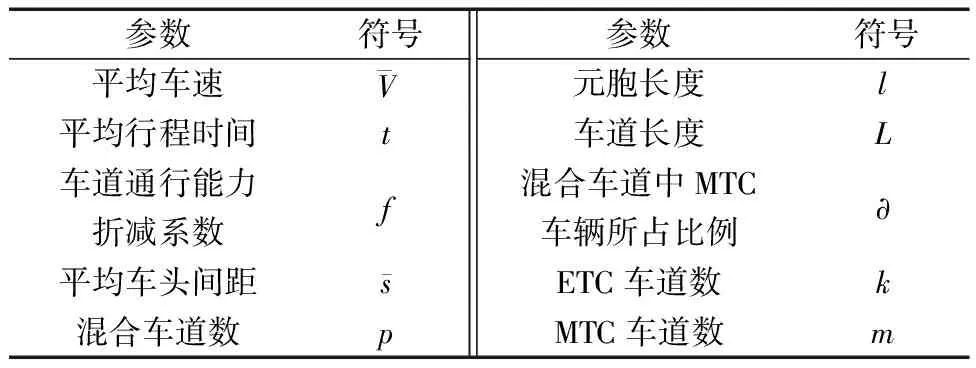
表1 需測量標定的參數

通過調查寧夏回族自治區的多個收費站的監控視頻,對站前廣場車輛的平均速度、平均通過時間和車道通行能力折減系數三個重要參數進行標定,為探究不同長度的站前廣場通行能力,選擇寧夏回族自治區部分具備調查條件的不同站前廣場長度的收費站,調查的部分收費站實景如圖3所示。

圖3 部分收費站監控視頻

通過調查寧夏回族自治區的多個收費站發現,大部分收費站站前廣場長度均在80～180 m、單向的收費口總數目在4～8個,其中以北京東路收費站、銀川南收費站、銀川東收費站、賀蘭收費站、吳忠收費站、六盤山收費站這六個收費站為調查對象,具體收費站信息如表2所示。為探究不同長度下的站前廣場通行能力,將對站前廣場為80、100、120、140、160、180 m的收費站進行研究探討。

3.大力倡導分享經濟新模式，利用閑置資源優化地方公共服務供給資源配置。人口老齡化加快會進一步增加養老、醫療與社會保障領域基本公共服務供給壓力，新的生育政策則會導致教育等基本公共服務需求迅速增加，導致基本公共服務供給缺口增加。為滿足人均可支配收入增加提高居民對高端生活服務的消費需求，治理公共服務供給缺口，應該大力倡導分享經濟新模式，進一步出臺有利于分享經濟發展的激勵政策，充分發揮教育、醫療、衛生、養老等公共服務領域的民間閑置提供能力，增強非基本公共服務的有效供給能力。

表2 收費站信息表

依托寧夏交投高速公路路網實時監控平臺,結合DSS Cloud遠程監控軟件采集寧夏回族自治區多個收費站視頻數據,分別統計在不同站前廣場長度情況下,ETC車輛和MTC車輛通過收費站的平均行程時間和平均車速數據,如表3所示。

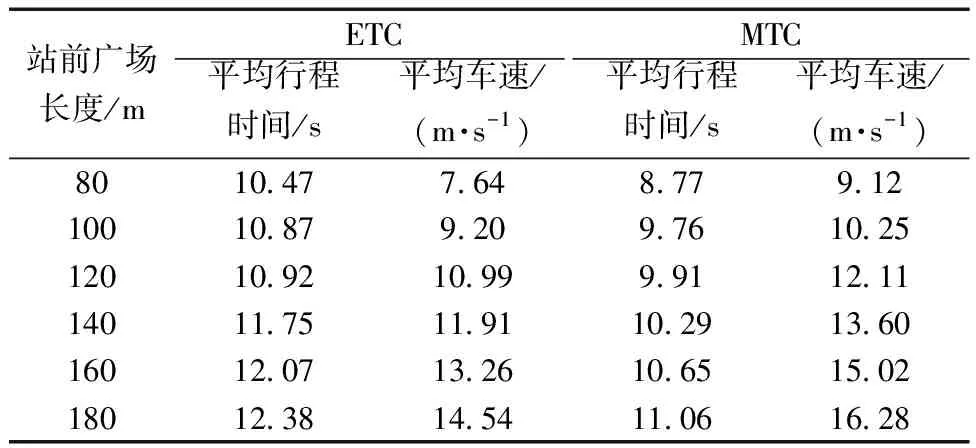
表3 平均車速和平均行程時間表

由表3統計的平均車速可以分析得出,隨著站前廣場長度的增加,平均車速在逐漸增大。主要原因是駕駛員進入站前廣場后不會立刻減速,而是會根據站前廣場的長度的大小先保持原本的車速行駛一段時間或加速行駛一段時間,等到靠近收費口時再進行減速。因為駕駛員是根據前方目測到收費口的距離進行加減速的判斷,當距離收費口越近,也就是站前廣場長度越短時,駕駛員會提前減速;當距離收費口越遠時,也就是站前廣場長度越長時,駕駛員會保持勻速甚至加速行駛至適當距離后再進行減速。

統計調查多個收費站不同車道的交通量,得到不同車道位置的ETC車道和MTC車道的交通量,根據式(9)計算,以收費站入口車道正對的車道為標準進行折減,得出相應的折減系數值,ETC車道、MTC車道折減系數分別如表4、表5所示。

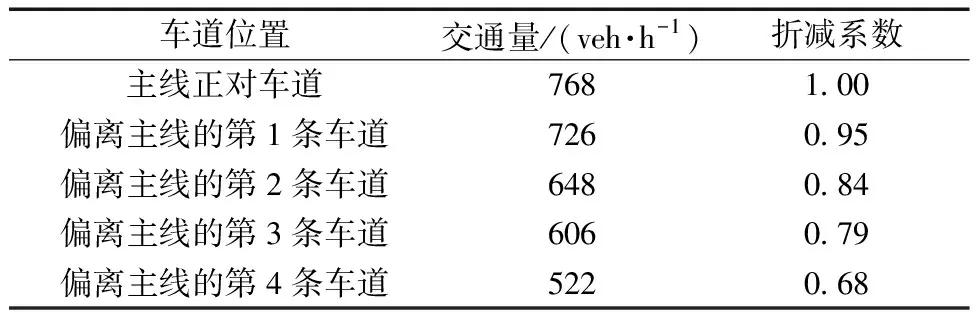
表4 ETC車道折減系數表

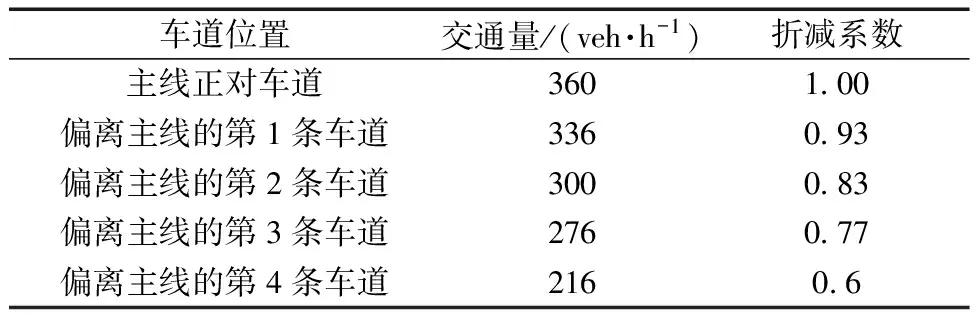
表5 MTC車道折減系數表

由表4和表5所統計的不同車道交通量結果可以看出,收費站入口正對的車道交通量最大,越偏離正對的車道所通行的車輛數越小。且MTC的折減比例會略大于ETC,其原因是因為當MTC車輛向偏離主線車道變道時,速度會比ETC車輛變道的速度更小,產生的通行能力折減程度就會越大。根據調查多個收費站的交通量統計所得的表4和表5分析可知,不論交通狀況如何,駕駛員都會更傾向于左側的收費通道。

2.2 不同站前廣場長度的通行能力

為驗證模型的普遍適用性,本文探討站前廣場長度為80、100、120、140、160、180 m,車道數目為4～6條的多場景下收費站站前廣場通行能力。ETC是收費站的未來發展趨勢,ETC車道數量至少為1條。因為中國ETC并未達到全覆蓋,MTC車道數量也至少為1條。于是討論總車道數目為4～6條,且ETC、MTC車道數量均至少為1條的情況下,不同ETC數量的通行能力。

根據式(11),以入口單車道收費站為例,計算不同站前廣場長度下不同車道配置的最大通行能力值如表6所示。

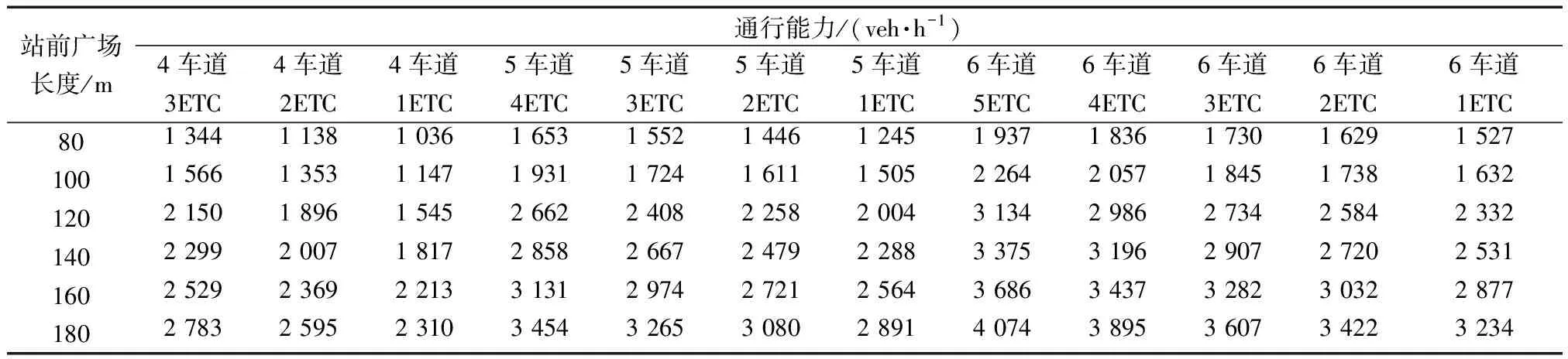
表6 入口單車道收費站不同長度、不同車道數量站前廣場通行能力

由表6計算的站前廣場通行能力值可得出,在車道總數相同的情況下,通行能力隨著站前廣場長度增加而增加;在站前廣場長度和車道總數均相同時,通行能力隨ETC車道數的增加而增大。

2.3 誤差分析

根據站前廣場通行能力模型與傳統意義的收費站通行能力有所不同,站前廣場通行能力是基于站前廣場的長度、車道位置等方面去計算站前廣場區域通行能力,并未考慮服務率對其的影響。為了驗證多場景下模型準確性,利用VISSIM軟件仿真模擬進行驗證,部分仿真參數如表7所示。

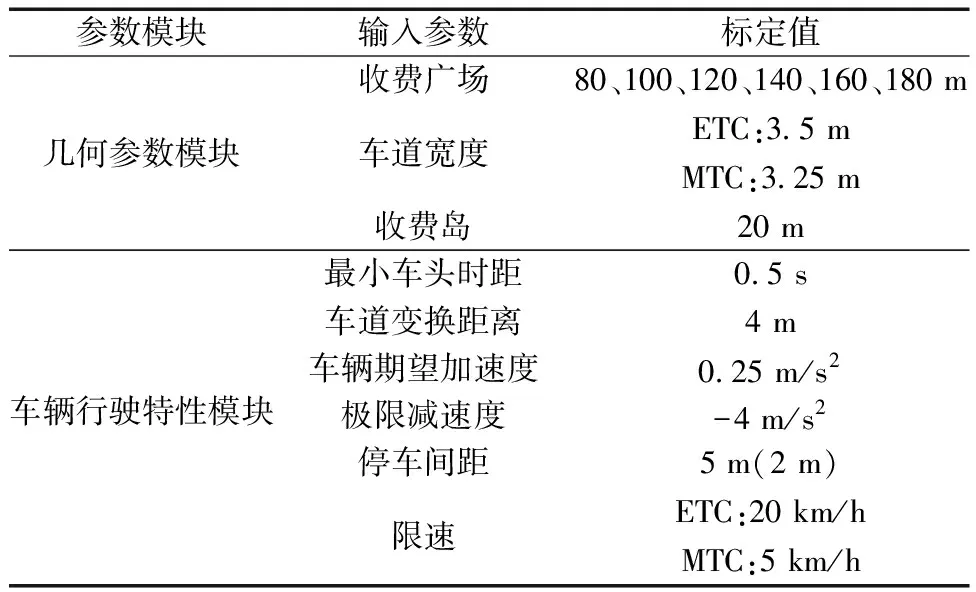
表7 仿真參數表

圖4 收費站仿真

選取了ETC車道數量最多的情況進行驗證,當ETC數量最多時,通行能力最大。為了使得仿真出的通行能力是最大值,從以下兩個方面來進行仿真方案設計:不同的車道配置和站前廣場長度。得到不同的站前廣場長度和車道配置情況下的站前廣場通行能力的仿真結果,以入口單車道收費站為例進行仿真,如表8所示。

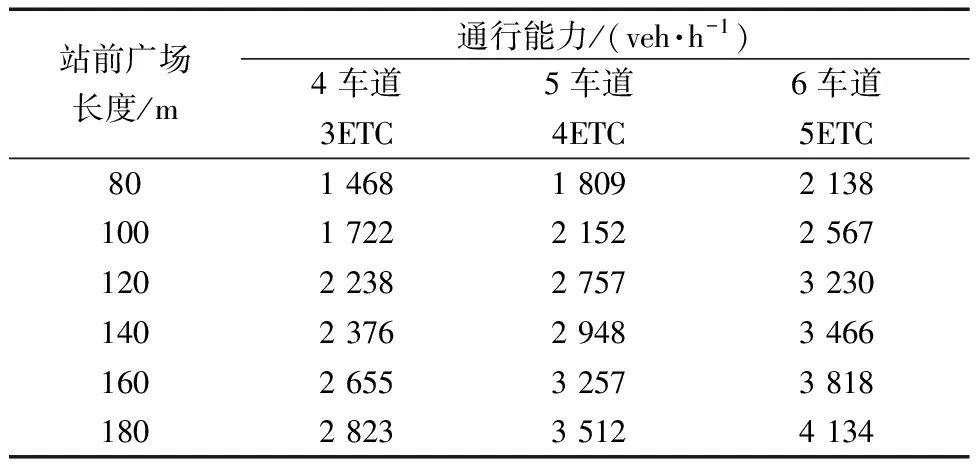
表8 仿真通行能力最大值

將三種車道配置下不同長度的站前廣場通行能力計算值和仿真值相互比較,分析隨站前廣場長度增加,站前廣場通行能力計算值和仿真的變化規律,如圖5所示。

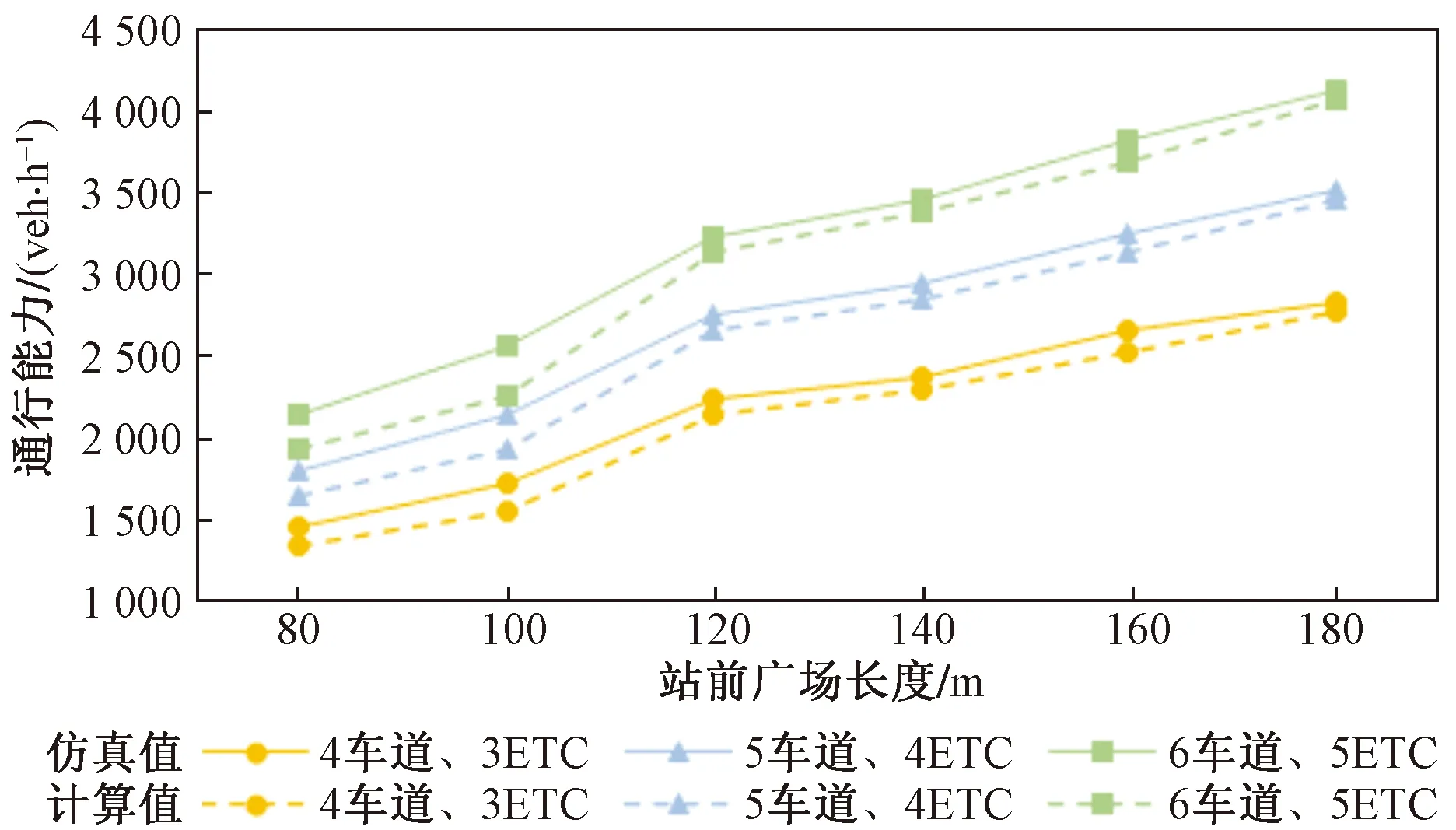
圖5 通行能力仿真值與計算值

由圖5可知,通行能力仿真值的規律與模型理論值所得結論一致,即隨站前廣場長度增加,通行能力值也隨之增加。為了驗證模型的有效性,需對其進行誤差分析,公式為

(12)

式(12)中:εj為總車道數為j條的通行能力計算值與仿真值之間的誤差;Xi為第i組數據通行能力的計算值;Yi為第i組數據通行能力的仿真值;m為數據總個數。

結合式(12)理論計算數據和仿真結果數據進行計算可得誤差如表9所示。

表9 理論值與仿真值誤差

結果表明:通行能力仿真結果與計算結果之間的誤差為5.19%。該誤差說明了仿真模型和計算模型的結果存在一定差異,分析原因如下。

(1)理論上的跟馳模型和仿真模型中的Wiedemann99存在一定的差異,且為了簡化計算理論模型中忽略了車身的長度,會產生一定的誤差。

(2)理論模型中的關鍵參數選取為平均速度,但實際上在元胞傳輸的過程中,速度的變化都是不一樣的,平均速度并不能很全面地反映整個速度的變化。

(3)仿真模型中,車輛對不同的車道進行了選擇,有些駕駛員甚至會進行兩次以上的換道,這種換道行為對通行能力的影響并不能完全在理論模型中反映出來。

針對以上產生誤差的原因,可以根據車輛類型來統計車輛的長度,同時考慮到速度變化和變道行為,將車輛長度、速度變化率和多次變道行為作為影響因素加入建模過程中。

從理論計算結果和仿真結果來看,仿真結果與理論計算結果基本吻合,可以很好地反映出隨著ETC車道數量和站前廣場長度的變化,混合收費站站前廣場通行能力的變化,并且誤差在可以接受的范圍內,說明理論模型與仿真模型具有較高的一致性。

3 結論

(1)考慮將收費站站前廣場的不規則區域劃分為規則的元胞,建立了收費站站前廣場通行能力模型,驗證結果誤差為5.19%,在可接受范圍內,具有一定的理論指導意義。

(2)調查不同站前廣場長度下的收費站可知:隨著站前廣場長度的增加,平均車速在逐漸增大;收費站入口正對的車道交通量最大,越偏離正對的車道所通行的車輛數越少。

(3)由不同條件下的站前廣場通行能力計算結果可知:在車道數量一定的情況下,通行能力隨著站前廣場長度增加而增加;在站前廣場長度和車道總數均相同時,通行能力隨ETC車道數目的增加而增大。

(4)可以使用此模型計算收費站站前廣場通行能力的顯示值,將計算所得的顯示值作為判斷擁堵程度的標準。當實際通行能力大于通行能力顯示值時,表明收費站產生了擁堵,需要采取相關措施進行疏散引導,避免交通癱瘓,提高通行效率,保障車輛暢通出行。