基于韋伯分布與RBI理論修正的加氫母站設備可靠性分析

周嬌,鮑磊*,于安峰,凌曉東,2,劉金玲,2,姜雪,2

(1.中石化安全工程研究院有限公司,化學品安全控制國家重點實驗室,青島 266000;2.中石化國家石化項目風險評估技術中心有限公司,青島 266000)

氫能以其清潔、高效、安全、可持續等優勢特點,被稱為20世紀最具發展潛力的能源[1]。近年來,中國氫能事業蓬勃發展,加氫母站的建設也逐漸興起,加氫母站是氫能供應鏈的終端環節,連接著上游制備與下游應用,其安全可靠性運營管理是氫能產業發展的關鍵所在[2]。同時,由于氫氣密度小極易擴散,易發生燃燒爆炸等特性,加氫母站或與其相似氫儲能園區的安全評價分析逐漸受到專家學者的研究關注[3-4]。與國外加氫母站相比,中國加氫母站建設時間較晚,在建設經驗、質量等方面存在一定的差距,加氫母站設備的失效數據也較少,很難從中獲取失效規律進行加氫母站的安全可靠性分析,因此相關的研究也處于初期階段。但設備失效的狀況會隨著設備服役時間而逐漸顯露,安全保障應防患于未然,才能使生產事故率降至較低水平,因此,加氫母站設備的失效數據統計與可靠性分析極為重要,這對于實現加氫母站的運行平穩有序及安全可靠具有重要意義。

針對加氫母站設備的安全可靠性分析,相關專家學者進行了一些研究。其中,葉召陽[5]通過介紹加氫母站工藝流程和主要設備,揭示了氫安全問題已經充斥在氫氣的制、儲、運和加氫母站等各個環節,亟需采用科學手段來保障氫安全問題,但如今針對加氫母站的安全分析研究處于起步狀態。阮錦添等[6]通過加氫母站工藝流程、操作關鍵點,探討運行過程中的隱患問題,并提出相應的措施對策。鄭津洋等[7-9]通過對氫能設備發展現狀的深入剖析,指出由于設計與使用問題,中國加氫母站設備存在疲勞失效的風險,但專家學者對于儲氫設備在失效模式、可靠性分析等方面的研究存在不完善之處與部分理論缺失,建議加強加氫母站設備數據庫建設與安全可靠性研究。陳曄等[10]對加氫母站的氫泄漏、火災、爆炸風險進行了梳理分析,并分析了加氫母站不同區域的消防安全措施。金星[11]對加氫母站進行了事故樹定性風險評估與事故的定量評估,并對從降低事故危害角度給加氫母站提出安全措施與建議。根據以上研究現狀可以發現,由于中國暫未建立氫能設備失效數據庫,大部分學者對于加氫母站的可靠性分析多是在理論框架、問題措施方面的定性研究,而對于加氫母站設備可靠性的定量研究較少,僅有的定量分析也多在失效后果分析方面,對于設備失效概率的量化多使用國外數據或專家經驗評判,準確性和適用性待查。但風險包括風險發生的可能性(即失效概率)和失效所造成的后果,除了定量分析后果影響外,定量化的失效概率分析也是準確量化失效風險中不可或缺的一環,否則可能造成風險量化不準確甚至不能識別設備風險導致更加嚴重的事故鏈后果。因此,加氫母站設備失效概率分析亟待探索與應用適應性強的研究方法,為加氫母站的安全生產運行提供重要參考依據。

鑒于此,現基于雙參數韋伯分布方法建立加氫母站失效數據統計分析模型,結合經典基于風險的檢驗(risk based inspection,RBI)理論,分析加氫母站特有失效機理模式,提出氫損傷修正因子,形成加氫母站設備可靠性分析模型,填補中國加氫母站設備可靠性分析方面的缺失,為找出加氫母站工藝流程中的薄弱環節以及運營、管理、決策提供參考。

1 研究方法

主要通過雙參數韋伯分布進行加氫母站失效數據統計分析,并計算獲得RBI理論中的底層數據,即設備同類失效概率,然后基于經典RBI理論分析加氫母站特有的失效模式,整體建立加氫母站設備可靠性的分析模型。

1.1 經典RBI理論及其修正

RBI理論是以設備的安全性與經濟性為前提,分析設備固有危險性與潛在危險性,為設備薄弱環節建立優化檢驗的方案,是目前國內外石化行業進行定量風險評估的先驅,并沿用至今。

根據RBI理論,可靠性量化指標中的失效概率F計算公式為

F=F同類FEFM

(1)

式(1)中:F同類為同類失效概率;FE為設備修正系數;FM為管理修正系數。

當設備的失效模式為材料相關金屬劣化時,FE稱為損傷次因子;當失效模式為低溫損傷、地震活動、開停車等這些特殊失效模式時,將其按性質的不同分別稱為通用次因子、工藝次因子和機械次因子[12]。盡管企業管理水平與設備故障模式無關,但它仍潛在影響著設備的失效,因此,管理修正系數作為一個單項列入修正模型中,其數值對于相同企業是固定的,與設備的性能無關。

基于RBI理論計算加氫母站設備失效概率,首先要統計計算設備的同類失效概率。同類失效概率是指利用行業內各種裝置的運行記錄、文獻資料以及商業數據庫得到的設備失效概率[13]。經典RBI理論中給出了某種典型設備在4種不同泄漏尺寸下(5、25、100 mm孔徑以及破裂)的同類失效概率,然而其對于加氫母站的設備而言不太適應,其管道的管徑較小、壓力較高,且運行環境也與經典RBI理論中的典型設備不同,因此對分類方法進行修正,經多方調研[14-17],采取泄漏孔徑比例分類,即分為0.01%、0.10%、1%、10%、100%五類進行分類,并針對氫設備特有失效模式設置修正因子進行后續計算。設備的實際失效概率為對每個泄漏孔徑比例下的同類失效概率進行修正后的概率之和,表達式為

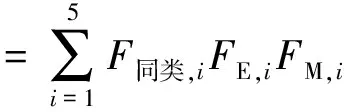
(2)

經典RBI理論中給出的典型設備同類失效概率對于中國加氫母站適應性不強,因為該數據大多來源于發達國家中煉化企業的設備失效案例,由于中國加氫母站在鋼材質量、設備制造工藝、介質性質、工作環境等方面與發達國家存在較大不同,因此對于中國加氫母站的設備可靠性評估,首先要收集中國加氫母站設備失效的數據,并計算出同類失效概率,才能更準確地評估加氫母站設備的可靠性。

1.2 雙參數韋伯分布

韋伯分布是一種極具有彈性的連續性概率分布,它可以描述設備在整個失效“浴盆曲線”上的概率分布,因此十分適用于加氫母站設備失效數據統計。韋伯分布可以分為雙參數的韋伯分布與三參數的韋伯分布,其區別在于三參數韋伯分布較雙參數韋伯分布增加一個位置參數,代表在x軸上的位置偏移程度,對于加氫母站設備而言,失效數據x軸為時間節點,不需要特定偏移,因此采用雙參數的韋伯分布更加適用。雙參數的韋伯分布概率密度函數表達式為

(3)

式(3)中:α為曲線的形狀參數,表征函數在形狀上的變化;β為曲線的尺度參數,表征函數在幅度上的變化;x為橫坐標,x≥0。

加氫母站設備可靠性量化指標選取失效概率為標準,則x為橫坐標,表示時間t,則設備的失效概率分布函數與失效率分布函數可分別表示為

(4)

(5)

當形狀參數α=1時,韋伯分布變為指數分布,指數分布也是一種常用于設備失效數據統計分析的分布函數,但從式(4)、式(5)可以看出,韋伯分布的失效率λ(t)為隨時間變化的函數,而指數函數中α=1,失效率為一常數,對于設備整個生命周期的適應性不強,僅可適應于統計設備在“浴盆曲線”的中間階段,即平穩運行期的失效數據,韋伯分布比指數分布的應用范圍更廣,更符合工程實際,因此,采用雙參數韋伯分布函數對加氫母站設備進行失效數據的統計分析。

2 加氫母站設備數據統計與可靠性分析

2.1 基于雙參數韋伯分布與極大似然估計的同類失效概率計算

通過雙參數韋伯分布統計計算設備的同類失效概率,首先要對韋伯概率分布函數中有兩個參數α和β進行估計。常用的參數估計方法有區間估計和點估計兩種。區間估計是對統計數據抽樣后估計其在一定置信度下總體分布的未知數,而點估計是通過樣本統計數據估計總體分布中的未知參數。區間估計比點估計更精確,但也更為復雜,甚至由于工作量的原因難以計算出結果。因此采用工程中常用的點估計方法中的極大似然法對韋伯函數中的參數α和β進行估計。

首先,構造分布函數的似然方程,即

(6)

然后,對式(6)兩邊取對數,并對α、β求偏導數,即

ln[L(α,β)]=nlnα-nαlnβ+

(7)

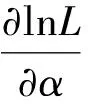
=0

(8)

(9)

最后,求得α、β的極大似然估計值,計算公式為

(10)

2.2 氫損傷修正因子研究

加氫母站設備失效概率為其同類失效概率、設備修正系數與管理修正系數之積。其中,同類失效概率可根據2.1節得出,而對于設備修正系數與管理修正系數,經典RBI理論中對于加氫母站的設備失效機理有一定的差異性,主要體現在加氫母站設備的失效機理以氫損傷導致的氫失效為主,還包含應力腐蝕、機械疲勞等,但RBI理論中缺乏氫失效相關的失效模式分析,因此對于氫失效模式下的設備修正系數進行分析,從而改進整體設備修正系數的準確度,所建立的加氫母站設備修正系數總圖如圖1所示。

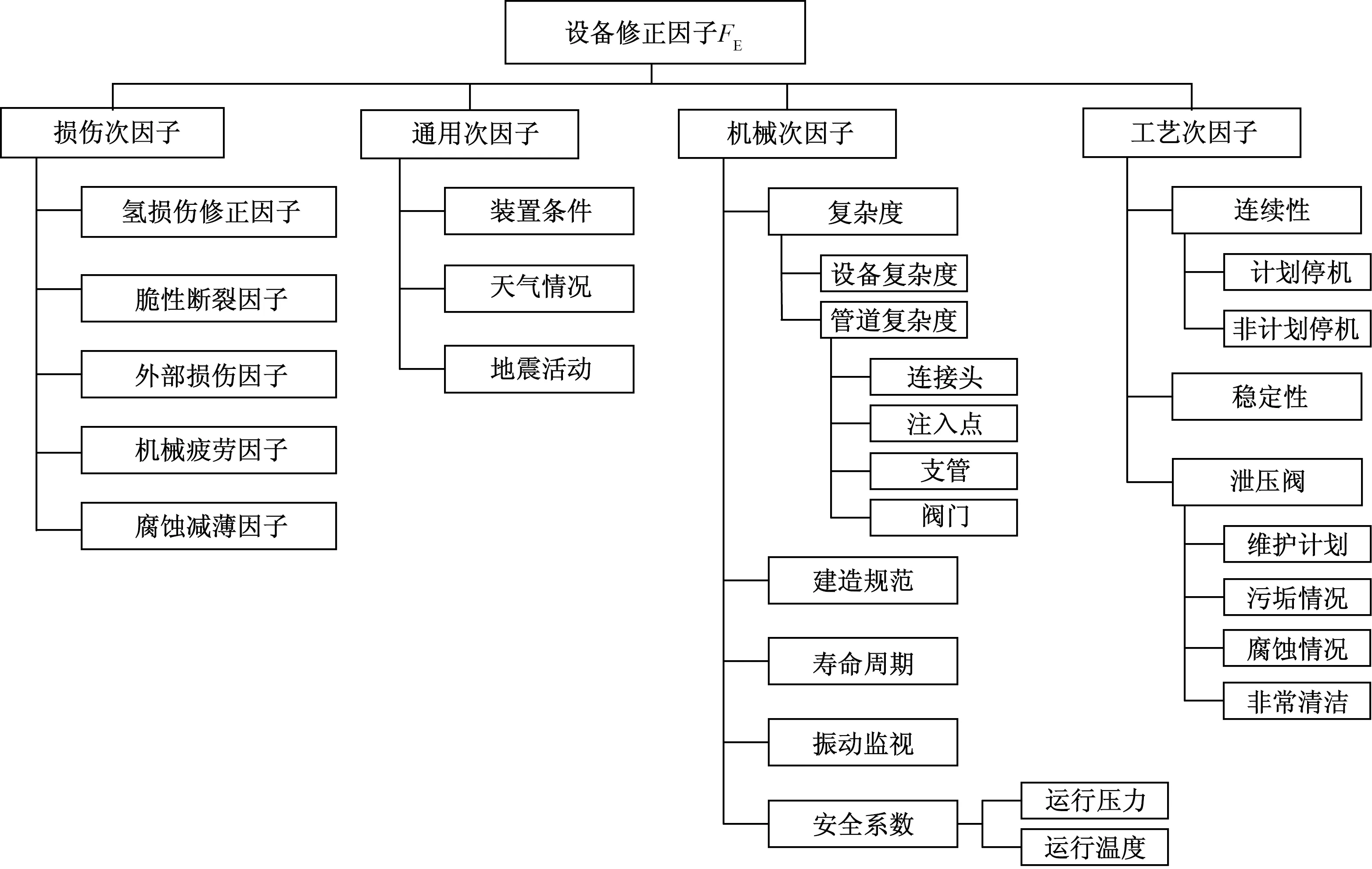
圖1 設備修正因子總圖

加氫母站設備修正系數由四個次因子組成,即損傷次因子、通用次因子、機械次因子以及工藝次因子,每個次因子又由多個評價要素組成,將每個要素所賦予的值相加,得到總的設備修正因子FE。

對于加氫母站,設備修正因子的改進主要體現在氫損傷修正因子(hydrogen corrosion correction factor,HCCF)上,該修正因子主要討論氫應力開裂(hydrogen stress cracking,HSC)、氫致開裂(hydrogen induced cracking,HIC)與應力取向氫致開裂(stress oriented hydrogen induced cracking,SOHIC)。

結合經典RBI理論[17],計算應力腐蝕開裂因子主要從檢驗有效性、敏感度與嚴重度三方面逐步分析。根據工藝、材料、制造參數將敏感性分為高、中、低三種等級,之后根據敏感性可確定嚴重度指數,最后再結合檢驗有效性可確定HCCF。

2.2.1 確定每種失效機理的敏感性

(1)氫應力開裂(HSC)。氫應力開裂(HSC)定義為一種金屬在拉伸應力和產生可擴散到金屬中的氫的腐蝕機理的共同作用下產生的開裂,一般發生在高強度(高硬度)鋼中或發生在低強度鋼的硬質焊接熔敷金屬或硬質熱影響區,結合RBI理論與專家討論,制定鋼材HSC的敏感性取值如表1所示。

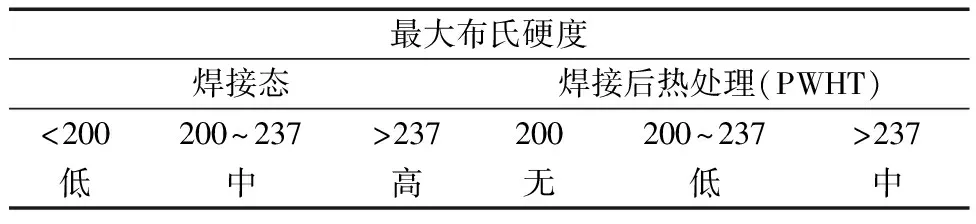
表1 鋼材的HSC敏感性

(2)氫致開裂(HIC)與應力取向氫致開裂(SOHIC)。氫致開裂定義為連接金屬內的不同平面上的氫鼓包或連接到金屬表面的階梯狀內部裂紋,其形成并不需要外部應力作用,開裂驅動力來自氫鼓包周圍的高應力,高應力是由于氫鼓包中的內壓力造成的。HIC的敏感性主要與鋼板的品質有關,也就是鋼板中不連續點的數量、大小、形狀,其中,鋼中的硫含量是一個關鍵的材料參數,降低鋼的硫含量可以降低鋼對氫鼓包和HIC的敏感性。

SOHIC定義為由于局部的高拉伸應力、由沿鋼板全厚度方向排列的氫致裂紋連接起來的小鼓包的堆疊陣列。SOHIC是HIC的一個特殊形式,通常出現在母材靠近焊縫的熱影響區,在該熱影響區存在高的殘余應力。同HIC一樣,鋼板的品質是SOHIC敏感性的一個關鍵參數。另外,通過焊接后熱處理(post weld heat treatment,PWHT)消除殘余應力,可以減少SOHIC的發生和嚴重度,但不能消除。

結合RBI理論與專家討論,制定鋼材HIC/SOHIC的敏感性取值如表2所示。

表2 鋼材的HIC/SOHIC敏感性

2.2.2 確定嚴重度指數

結合RBI理論與專家討論,制定HSC/HIC/SOHIC的嚴重度指數取值如表3所示。

表3 確定嚴重度指數

將2.2.1節中的敏感性結果輸入表3,確定每種潛在/已有氫損傷失效機理嚴重度指數。確定哪一種機理將導致最大嚴重度指數并以最大嚴重度指數作為最終結果。

2.2.3 檢驗有效性

檢驗有效性是按檢驗裂紋的預期效果進行分級。對于給定的檢驗技術或檢驗技術的組合,其實際效果取決于特定開裂機理的特點和其他因素。結合RBI理論與專家討論,制定HSC/HIC/SOHIC的檢驗有效性如表4所示。

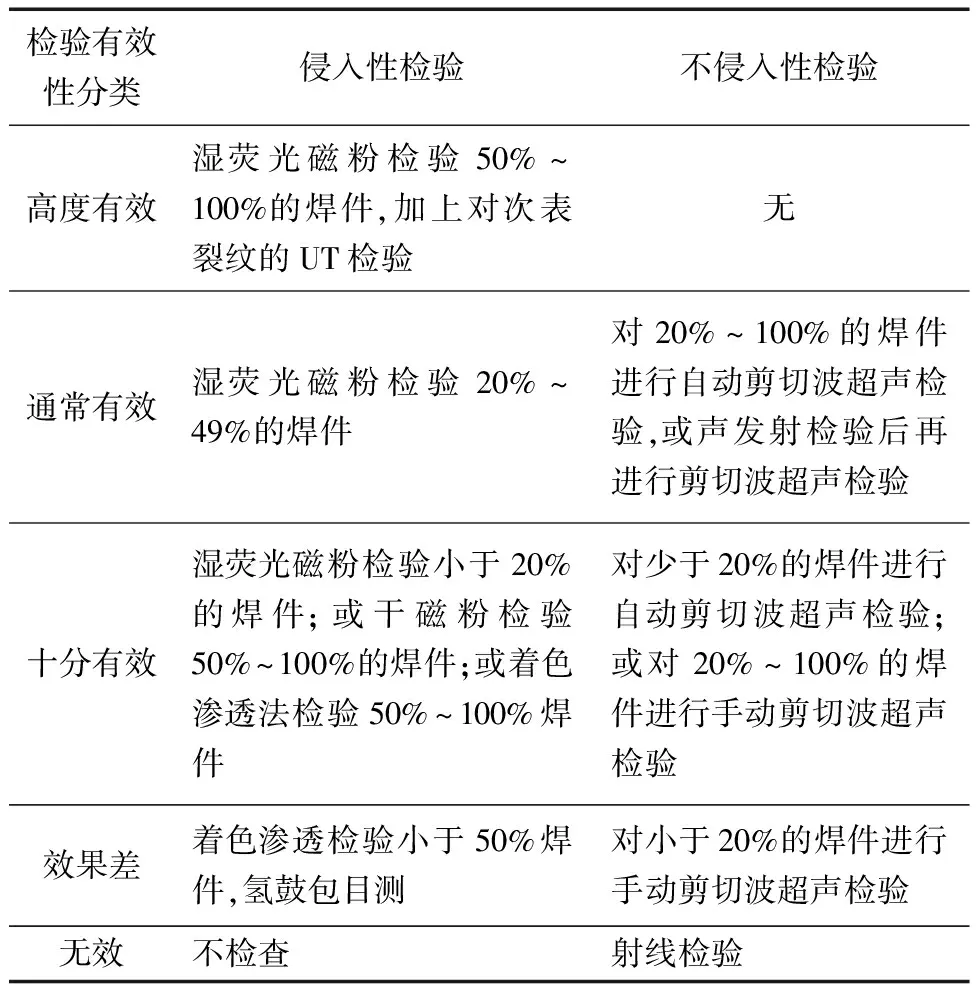
表4 HSC/HIC/SOHIC的檢驗有效性

根據敏感性、嚴重度和檢驗有效性即可確定HCCF取值,結合RBI理論與專家討論,制定HCCF取值如表5所示。

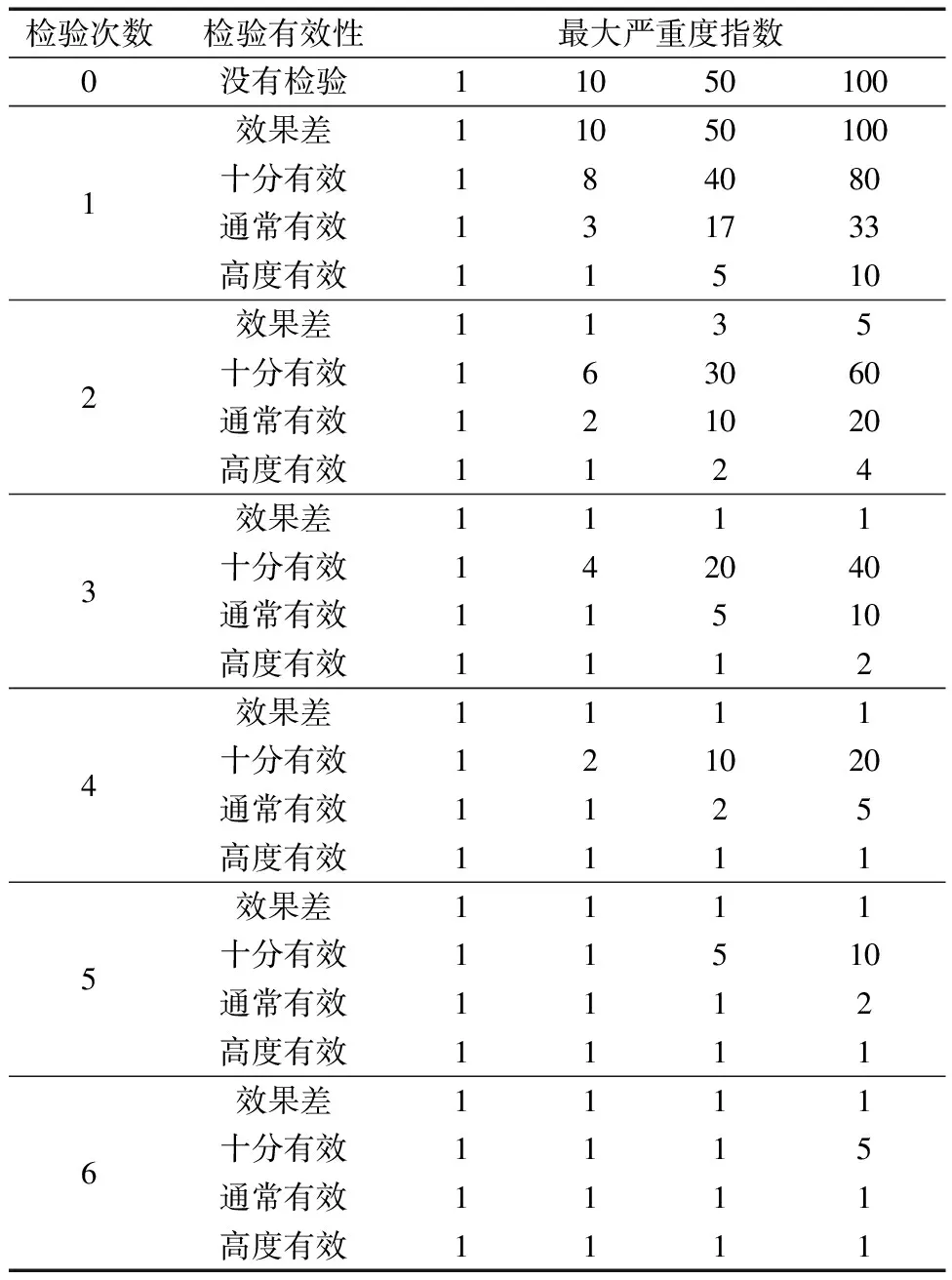
表5 HCCF取值

2.2.4 其他修正

(1)HCCF隨時間的增長。假設設備自上次檢測以來,由于暴露在異常條件和其他非正常條件下的時間增加,開裂的可能性會增加。因而,HCCF應當按下式修正:最終的HCCF=HCCF×(上次檢測以來的年數)。

(2)HCCF針對在線監測技術的調整。結合RBI理論與專家討論,除檢查外,使用氫氣探頭和/或關鍵工藝變量進行在線監測也會影響HSC/HIC/SOHICS的敏感性。在線監測可在發生重大裂紋損傷之前檢測到因工藝變更而導致的氫損傷敏感性變化。通過這種早期檢測一般可以采取及時的措施來降低故障的可能性。對于HSC/HIC/SOHIC,如果使用氫探頭或關鍵工藝變量監測,則在線監測因子為2;如果同時使用氫探頭和關鍵工藝變量監測,則在線監測因子為4。將HCCF除以在線監測因子得到最終的HCCF。如果HCCF為1,則不應用該系數。

3 示例分析

3.1 基于數據統計的同類失效概率計算示例分析

由于中國加氫母站失效數據庫暫未建立,因此采用假設數據。假設中國加氫母站在2012—2022年的10年間運行的30 014臺某類設備中,發生自然破壞而非爆炸、人為破壞等失效的設備為16臺,其中泄漏在(0,0.01D](D為管徑)內的設備為6臺,泄漏孔徑在(0.01%D,0.1%D]的設備為4臺,泄漏孔徑在(0.1%D,1%D]設備為3臺,泄漏孔徑在(1%D,10%D]的設備為3臺,泄漏孔徑(10%D,100%D]的設備有2臺,其分布如表6所示。

表6 不同泄漏孔徑設備數量分布

基于韋伯分布函數的統計方法,采用2.1節中的計算方法進行韋伯函數雙參數α與β的確定,結合牛頓迭代求解采用MATLAB編程可得到不同泄漏孔徑的α與β如表7所示。

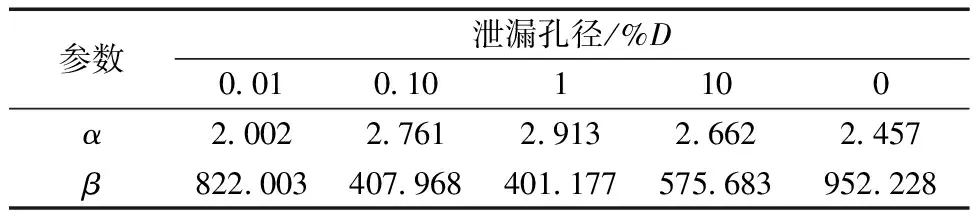
表7 不同泄漏孔徑下設備韋伯分布雙參數值

確定了α與β,再根據式(4),可以確定該類設備最終的同類失效概率,計算結果如表8所示。

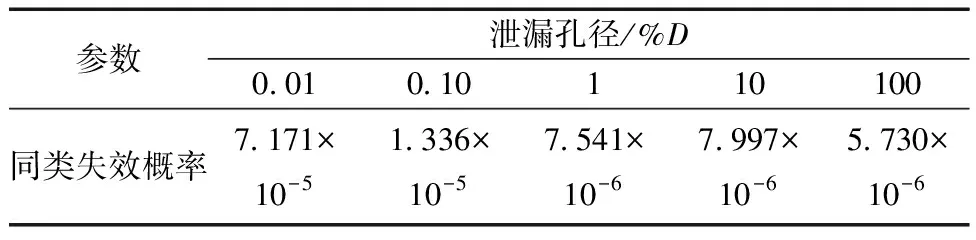
表8 該類設備同類失效概率計算結果

根據計算所得的同類失效概率,然后采用2.2節中的計算方法,即可計算出該類設備的失效概率。

3.2 基于RBI理論修正的加氫母站設備可靠性示例分析

根據3.1節中設備計算所得同類失效概率(表8),結合各類修正因子進行該設備失效概率的修正計算。

根據設備檢測數據分析可知該設備所發生或潛在發生的失效模式,從而確定損傷次因子中所取的修正因子類型。假設該設備為輸氫管道,發生了腐蝕減薄,且存在裂紋缺陷,因此在該設備計算損傷次因子時,主要考慮氫損傷修正因子、腐蝕減薄因子、脆性斷裂因子、外部損傷因子、機械疲勞因子。對于氫損傷修正因子,根據2.2節中的修正方法計算,計算結果如表9所示。

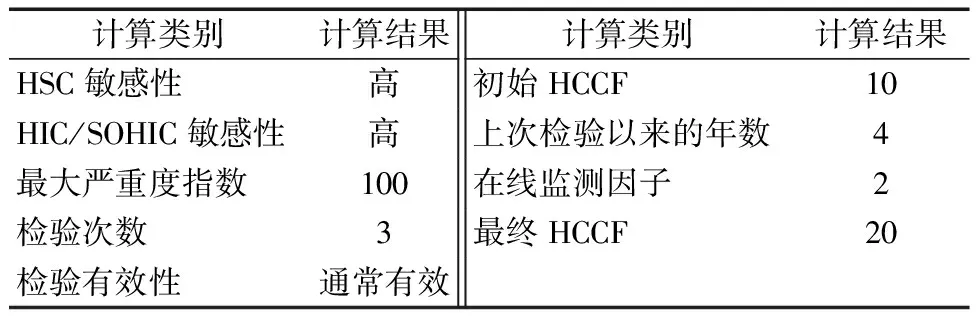
表9 氫損傷修正因子計算結果

對于腐蝕減薄因子、脆性斷裂因子、外部損傷因子、機械疲勞因子,可根據API 581中的計算方法進行計算,計算可得該設備的腐蝕減薄修正因子為2.15,脆性斷裂因子為12.59,外部損傷因子為0.75,機械疲勞因子為2,結合氫損傷修正因子,則設備的損傷次因子為37.49。同理,根據API 581中的計算方法,可計算出該設備的管理修正系數為0.65;可計算出通用次因子為4,機械次因子為3,工藝次因子為3,則設備修正系數為47.49。根據式(2)可計算得出該設備的失效概率為3.282×10-3。

3.3 氫損傷修正因子敏感性分析

在其他參數數值不變的情況下,對氫損傷修正因子進行敏感性分析,分析該因子對于設備最終失效概率的影響程度。不同氫損傷修正因子下,設備失效概率變化曲線如圖2所示。

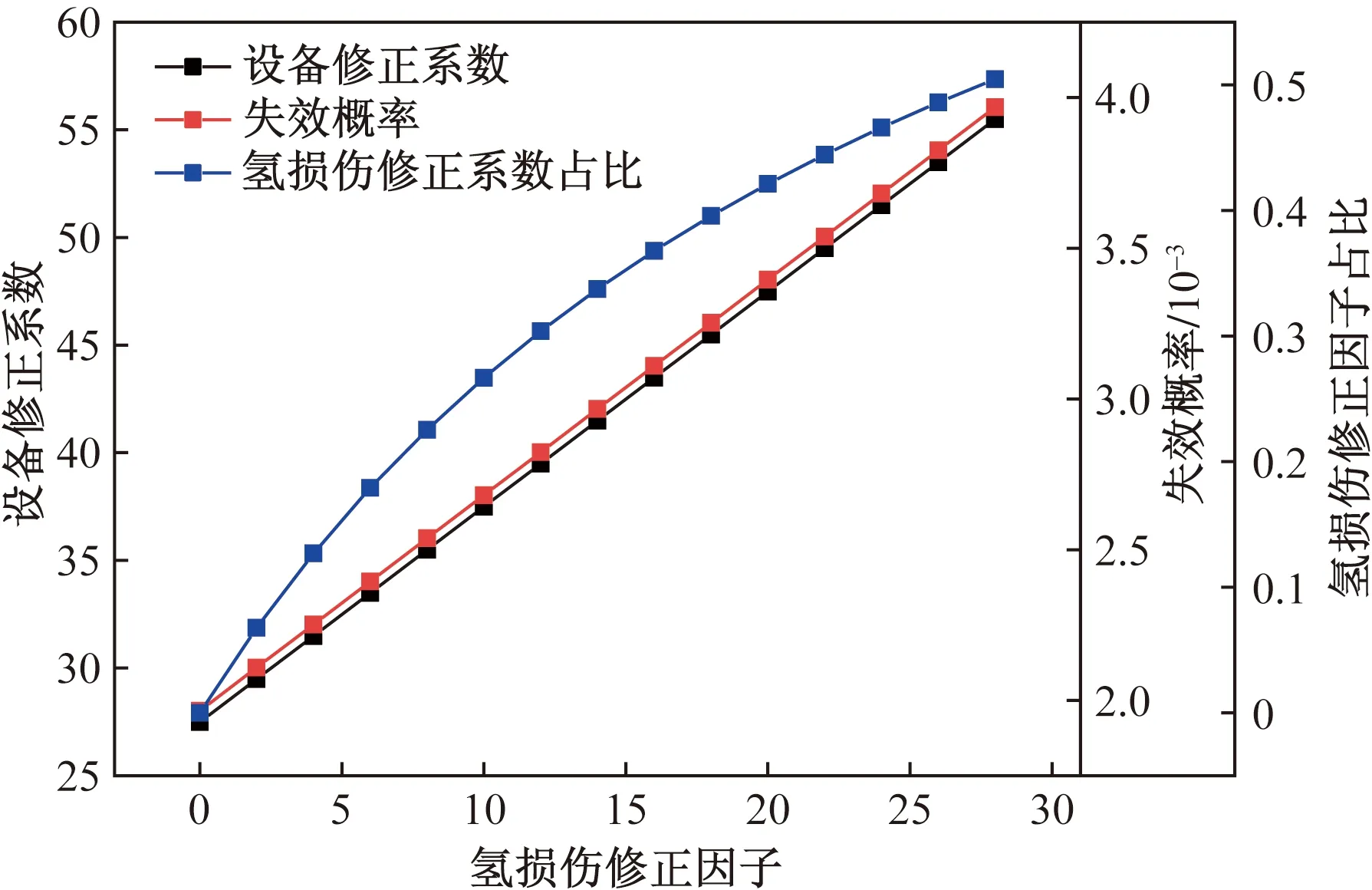
圖2 氫損傷修正因子敏感性分析

根據圖2可知,氫損傷修正因子對于設備失效概率呈正相關關系,而氫損傷修正因子最終結果取決于敏感度、嚴重度、檢驗有效性、檢測時間間隔、監測手段五類參數,設備敏感度越高,嚴重度越高,氫損傷修正因子越大,設備失效概率越大;檢驗有效性越有效或檢測時間間隔越長或監測手段越弱,氫損傷修正因子越大,設備失效概率越大。這是由于設備鋼材對于氫損傷越敏感,越容易發生失效;檢驗時間越長或監測手段越薄弱,越不容易發現設備出現的隱患,設備的失效概率也越大。隨著氫損傷修正因子的增大,其對于設備修正因子的占比越大,設備失效概率越大,氫損傷修正因子占比甚至可達50%,導致的設備失效概率也要翻倍。這是由于其他失效模式對于設備的失效概率影響相較于氫損傷都較弱一些,氫損傷一旦發生,設備失效速度會變得相對較快,這也說明了氫損傷失效模式對于氫設備是主要的失效模式,應采取措施進行預防性維護,比如采用敏感性較低的管材、盡可能豐富檢驗手段、縮短檢驗時間間隔、增加在線監測技術等,同時也要注意由于氫損傷造成的其他可能發生的失效模式對于設備的影響,從而共同保障加氫母站設備長周期的安全、平穩運行。

4 結論

(1)提出采用RBI理論進行加氫母站的可靠性分析,并對RBI理論針對加氫母站實際工況(泄漏孔徑分類)進行修正,采用雙參數韋伯分布結合極大似然估計統計分析加氫母站設備同類失效概率,為計算加氫母站設備同類失效概率提供一種新的方法,并為建立中國加氫母站設備失效數據庫提供方法參考。

(2)針對加氫母站設備特有失效機理,提出了氫損傷修正因子,并為之提供了定量分析的方法,通過示例分析得出該設備的失效概率值,有效解決了加氫母站設備對于氫損傷失效機理無法定量量化到失效概率中的問題,所提出的氫損傷修正因子結合了RBI理論基礎,包含氫損傷的常見失效模式,使設備的失效概率分析結果更加全面、準確。

(3) 對氫損傷修正因子進行敏感性分析,并分別具體分析了原因,得出氫損傷修正因子對設備失效概率呈正相關,隨著氫損傷修正因子對于設備修正因子的占比增大,設備失效概率越大,氫損傷修正因子占比甚至可達50%,導致的設備失效概率翻倍,建議對氫設備應采取一些具體措施進行預防性維護,對加氫母站設備安全運營管理與預防決策有重要意義。