基于PID控制的防抱死制動系統實現研究

呂懌萌

(煙臺汽車工程職業學院,信息與控制工程系,山東,煙臺 265500)

0 引言

隨著我國經濟的飛速發展,人們的整體經濟水平處于遞增趨勢,該現象使人們對生活質量的要求逐漸提高,并采用汽車代替傳統的出行方式。但是汽車在行駛過程中易出現抱死現象,嚴重威脅著人類的生命安全以及財產經濟,如何避免汽車防抱死現象的發生成為亟待解決的問題。汽車防抱死制動系統是一種科學有效的車用主動安全性部件,將該系統應用于汽車的緊急制動中,可有效消除汽車在制動過程中產生的不穩定因素。為此,本文利用PID控制建立防抱死制動系統,該系統可有效提高汽車的行車安全。

1 防抱死制動系統基本組成

汽車防抱死制動系統(ABS)包括氣壓和液壓兩種形式,不同形式ABS之間的差異性可體現在制動壓力方面,汽車防抱死制動系統在調整制動壓力過程中,充分結合不同形式的ABS,采取了不同的制動方案。不同形式汽車防抱死制動系統的基本組成單元存在一定相似性,該系統由傳感器、電子控制單元以及制動壓力調節單元共同組成。

1.1 輪速/車速傳感器

汽車防抱死控制過程中最重要的兩個參數為輪速和車速,該參數可通過車載電子傳感器進行實時獲取。車速傳感器只能應用于少數高端車輛中,產生該現象的主要原因為由于車速傳感器對精準度的要求較高,將該傳感器安裝在汽車內部時,無法實現汽車車速的精準測量,并且該傳感器在完成車速的測量過程中需要花費較高的成本。當前大部分車輛在安裝汽車防抱死制動系統時,僅采用輪速傳感器完成汽車輪速的獲取,再經過相應的手段計算出汽車的車速,以此實現汽車的防抱死制動控制。

1.2 電子控制單元(ECU)

該部分為汽車防抱死制動系統的核心單元,電子控制單元可充分利用傳感器上傳的數據信息,計算出汽車車輪的運動狀態,同時可實時獲取汽車的抱死傾向。為保證汽車動力輸出 的最大化以及汽車車輪的滾動狀態,結合計算結果對汽車防抱死制動系統的制動策略進行調整,并將制動力施加在汽車輪轂[1]。

通常情況下,電子控制單元內部包含16位單片機,該單元為實現汽車的防抱死制動控制,使自身具有極強的計算能力,同時內部帶有冗余備份,有利于提升電子控制單元的工作可靠性和處于速率。

1.3 制動壓力調節單元

該單元為汽車防抱死制動系統的關鍵部分,將該單元應用于汽車防抱死制動系統中,可實現信號變化到制動壓力變化的轉變,為汽車防抱死制動系統的執行機構。汽車防抱死制動系統可通過對制動液的流和制動氣室氣體的壓力進行調整,以此實現汽車制動力大小的調節,有利于提高汽車的穩定性。

2 防抱死制動系統模型構建

為實現汽車的防抱死制動,構建出防抱死制動系統模型。當前車輛行駛狀況仿真模型的常見類型包括單輪、雙輪、四輪以及一般車輛模型,四種不同類型的仿真模型之間存在一定關系。其中一般車輛模型將整車運動情況作為主要研究對象,可實現整車運動情況的完全模擬,該模型具有精度高、功能全面等特點。但該模型在實際應用過程存在復雜程度過高的問題,更適用于車輛的整體設計或者整車行駛情況的評估。四輪車輛模型可在一般車輛模型的基礎上建立,忽略一般車輛模型在實際應用過程中存在的影響因素,將一般車輛模型的車體部分作為質心,即可構建四輪車輛模型。四輪車輛模型可用于車輛運動特性的描述。而雙輪車輛模型主要在四輪車輛模型的基礎上構建,在實際應用過程中可將汽車的左右兩輪合并成一個車輪,該情況下的四輪車輛模型等同于摩托車模型,可適用于直線驅動、載荷轉移等問題的模擬。單輪車輛模型將車輛的制動性能作為主要分析對象,可研究汽車單輪的制動工況,該模型的建造過程較為簡單,可適用于ABS的建模分析。

2.1 單輪車輛制動系統數學模型

本研究對該模型進行設計時,為提升汽車的防抱死制動效果,將汽車的1/4作為主要研究對象,建立了合理有效、簡單適用的單輪車輛制動系統數據模型,該模型可符合系統的精度要求。為更好地突出單輪車輛制動系統數學模型的研究重點,在建立模型之前,提出多個假設條件:假設汽車車身和底盤與運載物體之間的連接關系為剛性;汽車輪胎的屬性為剛性,并且該輪胎無任何形狀的改變;汽車行駛過程中經過路面均為平整狀態,不存在任何顛簸的現象;車輛行駛方向為無側向、偏轉的直線;汽車車輪半徑在制動過程中無任何形狀的改變;車輪無陀螺效應的發生[2]。

基于上述假設條件,本文完成了1/4模型的簡化,單輪車輛制動系統數學模型如圖1所示。

圖1 單輪車輛制動系統數學模型

采用單輪車輛制動系統數學模型對汽車進行防抱死制動控制時,將模型車體的行駛方向和齒輪繞主軸方向作為核心自由度,在此基礎上完成動力學方程的建立,并將牛頓定律和達朗伯原理作為主要依據,可得到車輛的運動方程:

(1)

汽車車輪的運動方程為

(2)

車輪的縱向摩擦力公式為

Ft=Nμ

(3)

式(1)～式(3)中,M代表的含義為汽車車體的總質量(kg),V代表的含義為汽車車輪的中心速度(m/s),Fx代表的含義為汽車車輪在行駛過程中受到的縱向阻力(N),Fa代表的含義為汽車車輪在行駛過程中受到的空氣動力學阻力(N),I代表的含義為汽車車輪的轉動慣量(kg·m2),ω代表的含義為汽車車輪的角速度(rad/s),Ft=Fx代表的含義為輪胎與地面之間產生的附著力(N),Ff代表的含義為車輪的滾動阻力(N),Tb代表的含義為制動力矩(N·m),R代表的含義為汽車車輪的有效半徑(m),N代表的含義為汽車車輪對地面施加的法向反力(N),μ代表的含義為汽車車輪與地面之間的附著系數[3]。

Fa為汽車1/4車體在行駛過程中受到的空氣動力學阻力,其公式為

(4)

式中,ρ代表的含義為空氣的密度(kg/m3),Cd代表的含義為空氣動力阻礙系數,Adx代表的含義為汽車對空氣阻力的受力面積(m2)。

本研究對汽車車輪的滾動阻力進行計算時,其計算公式為

Ff=f0+3.24fs(Kmph×v)2.5

(5)

式中,f0代表的含義為基礎系數,fs代表的含義為速度影響系數,Kmph代表的含義為比例因子。

2.2 車輪輪胎模型

輪胎實際上是一種復雜黏彈性的結構,該結構具有非線性特性。學者將輪胎模型作為主要研究對象,對該模型進行深入研究,并取得了一些成果。常見的輪胎模型可劃分為三大類:其一,將輪胎試驗數據作為主要依據,以此建立可描述輪胎側偏特性的模型,例如Magic Formula模型;其二,對輪胎與路面之間的關系以及作用機理進行深入研究,研究得出的理論基礎可為模型提供理論支撐,例如Fiala模型、Gim模型等;其三,將試驗數據作為核心,擬合出相應的理論模型,通過對模型的參數和理論充分結合,以此構建出半經驗模型,例如MF-Tyre模型。

通過對上述模型進行分析可知,理論模型的精度較低,但該模型在實際應用過程中,無需進行試驗數據的擬合。經驗模型和半經驗模型的精度遠高于理論模型的精度,但經驗模型和半經驗模型在實際應用過程中,均需進行試驗數據的擬合。不同類型的模型適用的領域存在差異性,由于車輪輪胎模型在仿真過程中需要重復調用。因此,本文在選用模型時,應充分考慮模型的計算效率與精度。本文對該模型進行設計時,選用Pacejka HB的魔術輪胎模型作為該模型的設計基礎,有利于提高計算的效率和精度[4]。在Magic Formula魔術公式的基礎上,設計車輪輪胎模型。對汽車進行防抱死制動時,汽車車輪的滑移率和縱向附著系數之間的函數關系為

μ(λ)=f+Dsin{C·arctan[B·λ-

E(B·λ-arctan(B·λ)]}

(6)

式中,f代表的含義為輪胎的靜摩擦系數,D代表的含義為峰值因子,B為剛度因子,C代表的含義為曲線形狀因子,E代表的含義為曲線曲率因子,λ代表的含義為滑移率,μ代表的含義為縱向附著系數。

2.3 制動系統模型

本文對汽車制動系統的模型進行構建時,選用液壓式制動系統作為研究對象。制動器包含3種狀態,不同的狀態均可與液壓控制閥的不同位置之間進行對應。當制動器的回油路處于相通狀態時,制動缸為減壓模式;當控制閥處于關閉狀態時,制動缸為保壓模式;當制動器的油源與輪缸接通時,制動缸為增壓保壓模式[5]。

假定油源的壓力為常數,油源進入制動缸的流量Q公式為

(7)

式中,A代表的含義為控制閥的過流面積,Cd代表的含義為控制閥的流量系數,ρ代表的含義為油液密度,P代表的含義為制動缸壓力,Ps代表的含義為油源壓力。

對活塞的運動速度進行計算時,可忽略油液的可壓縮性,其公式為

(8)

式中,AP代表的含義為油缸作用面積。油液被壓縮的變化率公式為

(9)

式中,βe代表的含義為油液體積的彈性模量,VD代表的含義為油缸和管路的容積。通過對式(5)～式(7)進行整理,可得到的公式為

(10)

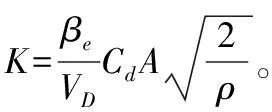
(11)

若忽略系統受非線性因素和溫度因素的影響,可將制動力矩Tb看作制動壓力P的線性函數:

Tb=(P-Pout)AwcηBFrr

(12)

式中,Pout為推出壓力,Awc代表的含義為輪缸面積,η代表的含義為機械效率,BF代表的含義為制動因子,rr代表的含義為有效轉子半徑[6]。

通過對式(10)進行簡化可得到:

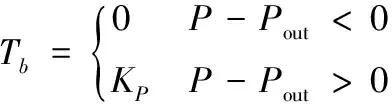
(13)

為實現制動力的調節,本文對制動系統進行設計時,將控制器的電磁閥指令作為主要依據,并對控制器進行保壓、減壓、增壓等操作,使汽車車輪的滑移率維持在最佳值。

3 PID控制基本原理

3.1 PID控制基本原理

PID控制與邏輯門限值控制之間存在一致性,在實際控制過程中均不依賴汽車防抱死制動系統的數學模型,并且該控制方式的原理較為簡單,可在不受任何應用場合限制的情況下,實現汽車的防抱死控制,具有生命周期長、可靠性高等特征。

PID控制內部控制量u和誤差e之間的傳遞函數公式為

(14)

式中,U(s)代表的含義為控制量u的拉氏變換,E(s)代表的含義為誤差e的拉氏變換,KP代表的含義為比例(P)系數,Ki代表的含義為積分(I)系數,Kd代表的含義為微分(D)系數[7]。

在PID控系統制中,控制量u主要由誤差e的比例、積分、微分等分量經過線性組合而形成的,3個分量對汽車防抱死制動系統均含有調節作用,不同分量的調節作用各不相同。對誤差e進行計算時,可預先計算出給定值r(t)和實際值y(t),二者之間的差即為誤差值。PID控制結構如圖2所示。

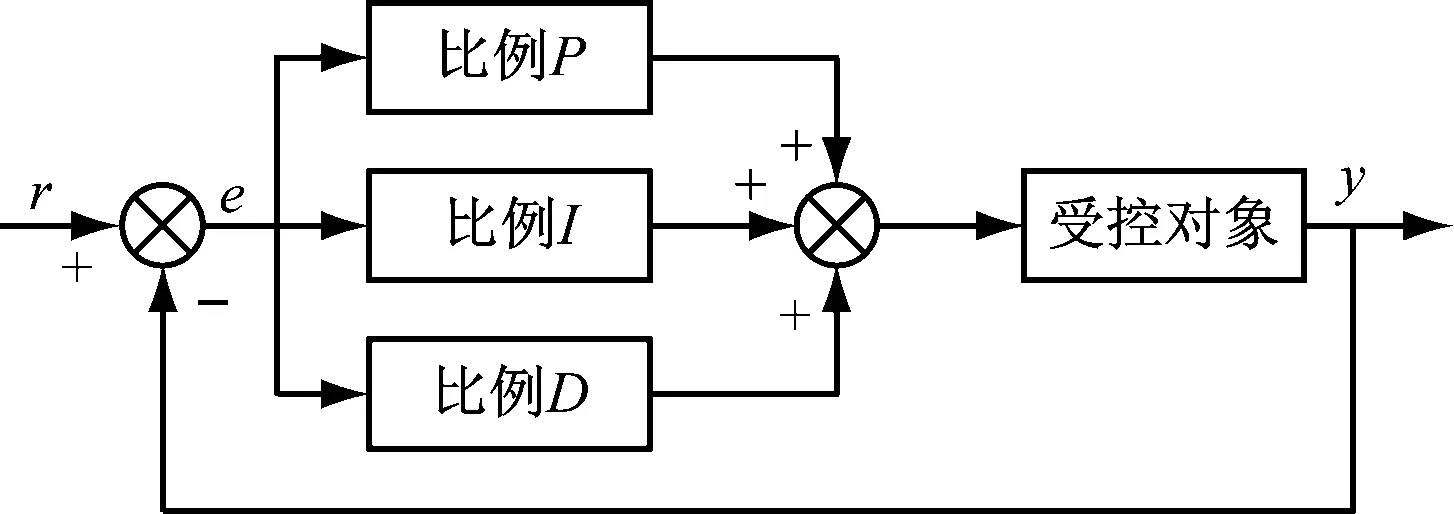
圖2 PID控制結構圖

本文為了后期對系統進行仿真設計,對PID控制律進行離散化,其公式為

(15)

式中,u代表的含義為控制量,e代表的含義為誤差數值,u0代表的含義為控制量初值,KP代表的含義為比例積分系數,Ti代表的含義為積分時間常數,Td代表的含義為微分時間常數,T代表的含義為采樣周期。

當采樣周期的取值處于較小狀態時,即可達到系統的控制精度。采用數字式PID對系統進行控制時,可利用遞增式算法對其進行計算,其公式為

Δu(k)=u(k)-u(k-1)=Kp[e(k)-e(k-1)]+

Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)]

(16)

3.2 PID控制參數

本文對PID控制器的參數進行設計時,將滑移率控制的基本原理作為主要依據,制定出PID控制策略。該控制策略的具體內容為:當滑移率大部分曲線位于I區時,防抱死制動系統存在較大誤差,并且該系統的響應速度較慢,為適當地加快防抱死制動系統的響應速度,并最大限度地減小防抱死制動系統的誤差現象,可增大Kp、減小Kd;當滑移率大部分曲線位于Ⅱ區時,防抱死制動系統無法精準控制車輛,為提高系統的穩定性,可適當地抑制超調,增大Kd、減小Kp;當滑移率大部分曲線位于Ⅲ區時,防抱死制動系統可精準控制車輛,為取得更好的控制效果,可在保證Kd和Kp處于穩定狀態時,對Ki進行調節。通過PID控制策略,可對高、中、低三種不同附著系數的路面進行整定,整定過程中獲取的參數可用于仿真。防抱死制動系統輸出響應曲線如圖3所示。

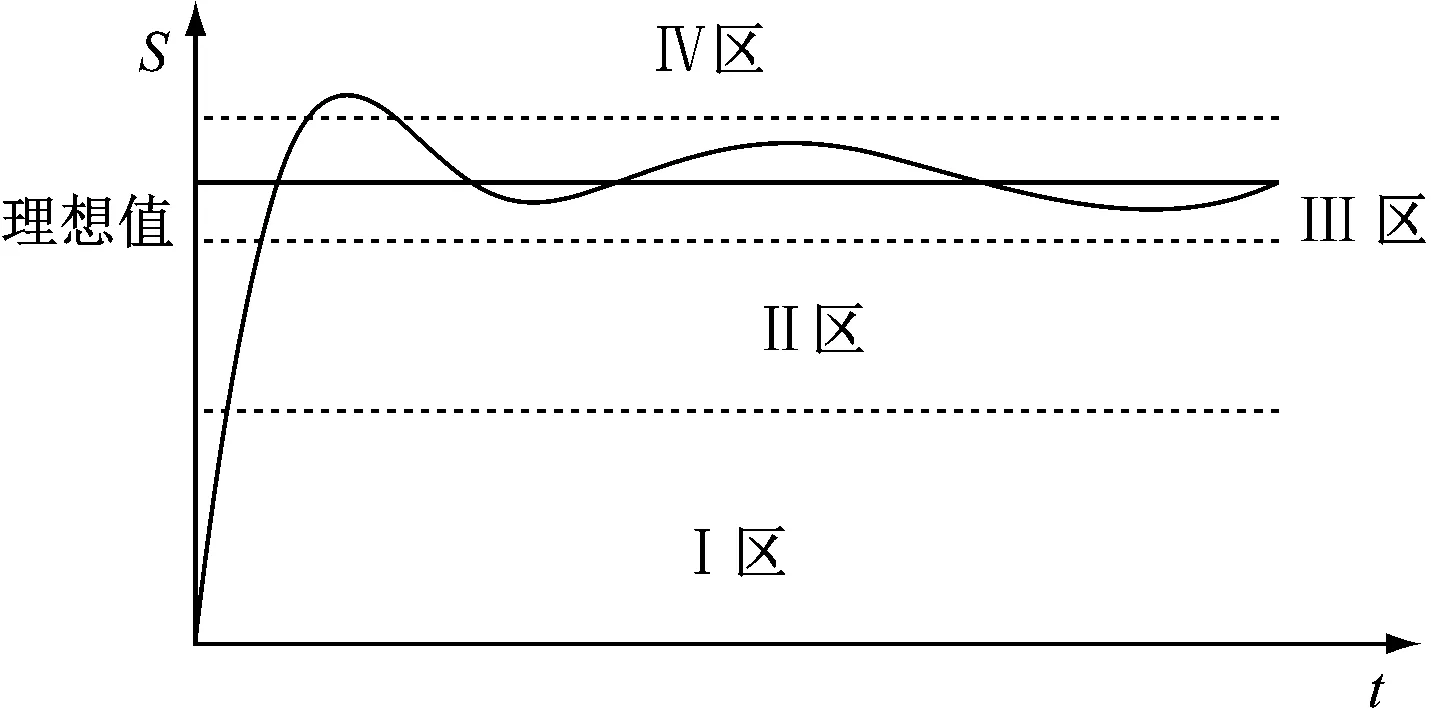
圖3 防抱死制動系統輸出響應曲線

PID控制器設計的目的是為了實現P、I、D參數的整定,對參數進行整定時,可采用試湊法作為參數整定的核心方法。試湊法整定過程:首先,為初步達到控制車輛的目標,對參數的比例進行整定;其次,對積分和微分兩部分進行整定;最后,調整防抱死制動系統的超調、穩定性以及響應速度等,通過系統的參數進行反復修改,最終得到滿意的效果。PID控制參數如表1所示。

表1 PID控制參數

4 基于PID控制的防抱死制動系統制動仿真

本文為驗證ABS系統的有效性,將邏輯門限值作為ABS系統的核心算法,在該算法的基礎上完成ABS控制器的建立,并在相同條件下對處于濕瀝青路面的ABS系統的制動過程進行仿真。為簡化系統仿真過程,采用單門限控制邏輯完成系統仿真,將最佳參考滑移率作為ABS系統的控制門限,以此實現對系統的調節。基于PID控制的防抱死制動系統控制邏輯如圖4所示[8]。

圖4 基于PID控制的防抱死制動系統控制邏輯

圖中濕瀝青路面對應的λmin=0.1108,λmax=0.1508,最佳滑移率的參考值為λR=0.1308。邏輯門限控制的ABS制動仿真曲線如圖5所示。

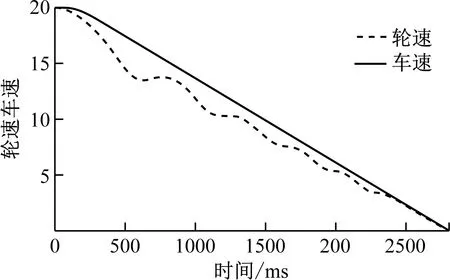
(a) 輪速隨車速的變化趨勢

通過對邏輯門限控制的仿真結果進行分析可知,該算法可有效進行ABS控制,在汽車進行制動過程中汽車的車輪可隨著車速的變化而變化,并且汽車車輪為發生抱死現象,較好地實現了制動控制。

5 總結

本文為提升汽車的防抱死制動效果,將汽車的1/4作為主要研究對象,建立了合理有效、簡單適用的單輪車輛制動系統數據模型,該模型可符合系統的精度要求。為實現制動力的調節,本研究對制動系統進行設計時,將控制器的電磁閥指令作為主要依據,并對控制器進行保壓、減壓、增壓等操作,使汽車車輪的滑移率維持在最佳值。為驗證ABS系統的有效性,將邏輯門限值作為ABS系統的核心算法,在該算法的基礎上完成ABS控制器的建立,并在相同條件下對處于濕瀝青路面的ABS系統的制動過程進行仿真。邏輯門限控制的仿真結果表明,該系統可實現汽車的防抱死制動,并且在測試過程中汽車車輪未發生抱死現象,較好地實現了汽車的制動控制。