T型微帶線傳導干擾的時域建模分析方法

葉志紅，張 玉，程亞軍，魯唱唱，李汸陽，詹超然

(重慶郵電大學 通信與信息工程學院，重慶 400065)

0 引言

隨著無線技術的快速發展,小型化和高集成度已然成為集成電路的發展方向。受集成電路電磁兼容性設計要求的制約,集成電路各元件和電路模塊之間的互聯線呈現多種彎折結構,T型微帶線是其中較為常見的一類結構,當干擾信號流經T型微帶線時,在連接節點處會出現電荷聚集效應,使得該點的阻抗特性發生變化。因此,開展T型微帶線的傳導干擾建模分析方法研究,準確計算干擾信號在T型微帶線上的瞬態響應,可為集成電路板級信號完整性分析提供重要技術支撐。

目前,國內外學者基于傳輸線理論,提出了多種高效的數值算法,用于印刷電路板(Printed Circuit Board, PCB)上微帶線的傳導干擾分析。其中,Baum-Liu-Tesche(BLT)方程方法[1-5]和傳輸線方程的時域有限差分(Finite-Difference Time-Domain, FDTD)解法[6-10]應用最為廣泛。

傳統BLT方程方法基于電磁拓撲理論,通過節點和管道的形式建立集總干擾源與微帶線連接節點及端接負載響應的聯系,并對構建的關系矩陣進行求解得到負載上的電壓和電流響應。但是,當集總干擾源為寬頻帶信號時,計算效率會急劇降低。同時,BLT方程只能獲得端接負載上的電壓電流,無法求取微帶線沿線各點的電壓,不利于后續開展二次輻射仿真。盡管頻域BLT方程已被部分學者應用卷積運算擴展到了時域,但是卷積運算需要存儲大量的歷史時刻電壓、電流數據,計算過程復雜且效率低下。傳輸線方程的FDTD解法是一類時域算法,其使用傳輸線方程構建微帶線的傳導干擾模型,并對傳輸線方程使用FDTD[11-12]的中心差分格式進行求解,獲得微帶線沿線及其端接負載的瞬態響應。然而,該方法尚未用于T型微帶線這類特殊微帶線結構的傳導干擾建模與仿真分析。

因此,本文基于傳輸線方程,結合電荷守恒定律,并引入高階FDTD(2,4)方法,研究一種高效的時域混合算法,在避免對T型微帶線精細結構直接建模的情況下,實現T型微帶線傳導干擾的時域快速仿真。

1 時域混合算法理論

時域混合算法實現T型微帶線的傳導干擾分析,需要將T型微帶線進行分解,形成多段獨立的直微帶線和連接節點結構,并分別使用高階FDTD(2,4)方法和電荷守恒定律進行傳導干擾建模與計算。下面將從直微帶線傳導干擾的高階FDTD(2,4)求解和基于電荷守恒的連接節點電壓計算兩方面,詳細闡述時域混合算法的具體實施方法。

1.1 直微帶線傳導干擾的高階FDTD(2,4)求解

一般,微帶線與接地板之間的距離小于干擾源最高頻率對應的最短波長,可以忽略微帶線的輻射效應。此時,應用傳輸線方程構建每段直微帶線的傳導干擾模型,表示為:

(1)

(2)

式中:I(y,t)、V(y,t)分別表示直微帶線沿線各點的電流和電壓,C、L分別表示直微帶線的單位長度電容和電感,可使用有限元法對直微帶線二維橫截面進行建模并提取得到。

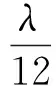
(3)

Vn+1(k)=Vn(k)-

(4)

式中:k表示各段直微帶線上電壓和電流沿線各點的位置,取值為2,3,…,N-2。

從式(3)和式(4)可以看到,FDTD(2,4)的迭代方式不適用于直微帶線始端和終端的電壓,以及始端和終端相鄰節點處的電流和電壓。因此,對于微帶線兩端電壓需要使用前向差分和后向差分進行處理,其相鄰節點處的電壓電流,需要采用傳統FDTD的中心差分格式進行求解,具體的迭代公式見文獻[16]。

1.2 基于電荷守恒的連接節點電壓計算

T型微帶線的連接節點是各段直微帶線的共用端口,節點處的電壓無法使用傳統FDTD或者高階FDTD(2,4)的差分格式求解得到。T型微帶線連接節點處的電荷守恒應用如圖1所示,考慮到節點處的電壓是連續的,因此使用電荷守恒定律構建連接節點處電壓與各段直微帶線上電流之間的關系方程,表示為:

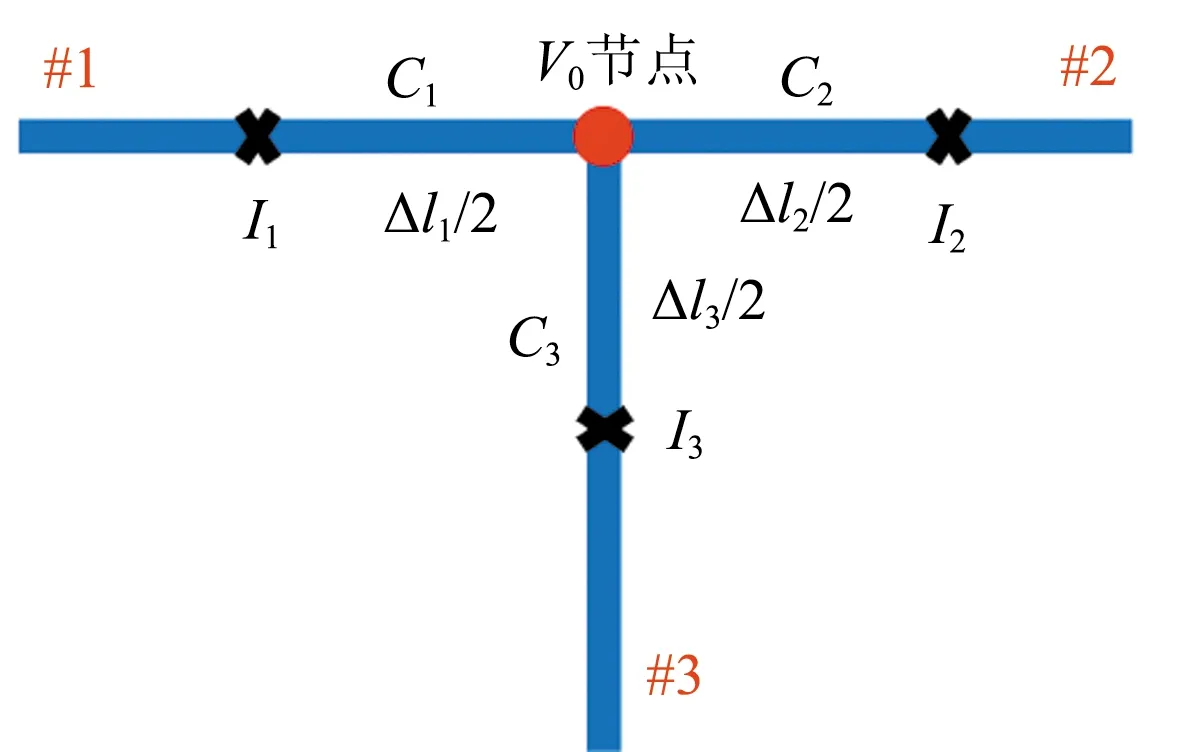
圖1 連接節點處的電荷守恒應用Fig.1 Charge conservation application at connecting node

(5)

式中:V0為節點處的電壓,Δl1、Δl2和Δl3分別為直微帶線#1、#2、#3進行網格劃分的空間步長,C1、C2、C3分別為直微帶線#1、#2、#3的單位長度電容參數,I1、I2、I3分別為微帶線#1、#2、#3上鄰近連接節點的電流響應。

采用FDTD中心差分格式對式(5)進行離散,獲得T型微帶線連接節點處電壓的迭代計算式為:

(6)

2 數值仿真分析

使用時域混合算法對單個T型微帶線結構和多個T型微帶線組成的網絡結構進行傳導干擾計算,并與BLT方程和電磁仿真軟件CST的仿真結果進行對比,驗證該算法的計算精度與效率。

單個T型微帶線的傳導干擾模型如圖2所示,接地板設為理想導體,基板大小為5 cm×6 cm,厚度為1 mm,材料的相對介電常數為5。T型微帶線位于基板上表面,由3段直微帶線#1、#2、#3構成,長度分別為4、2、3 cm,寬度為2 mm,厚度為0.034 mm。微帶線#1始端接有高斯脈沖電壓源,幅度為10 V,脈寬為4 ns。直微帶線#2、#3的端接負載為R1=R2=50 Ω。使用有限元法對直微帶線對應的二維橫截面進行建模,提取得到的直微帶線單位長度電感和電容分布參數分別為L=290.22 nH和C=143.09 pF。

圖2 單個T型微帶線的傳導干擾模型Fig.2 Conducted interference model of a single T-shaped microstrip line

BLT方程、CST和時域混合算法仿真得到的負載R2上的電壓響應如圖3所示。為了更加客觀地評價時域混合算法的精度,使用特征選擇評估(Feature Selective Validation,FSV)方法[17-18]對3種方法的仿真結果進行幅度差異分析。BLT方程和時域混合算法的計算結果與CST仿真結果的幅度差異量(Amplitude Difference Measure,ADM)直方圖如圖4所示。可以看出,時域混合算法與CST仿真結果的幅值吻合度達到很好以上等級的比例為100%,而BLT方程僅為90%,驗證了該算法的精度能夠與CST全波仿真保持完全相同,且優于BLT方程。

圖3 3種方法計算得到的負載R2上的電壓響應Fig.3 Voltage responses on the load R2 calculated by the three methods

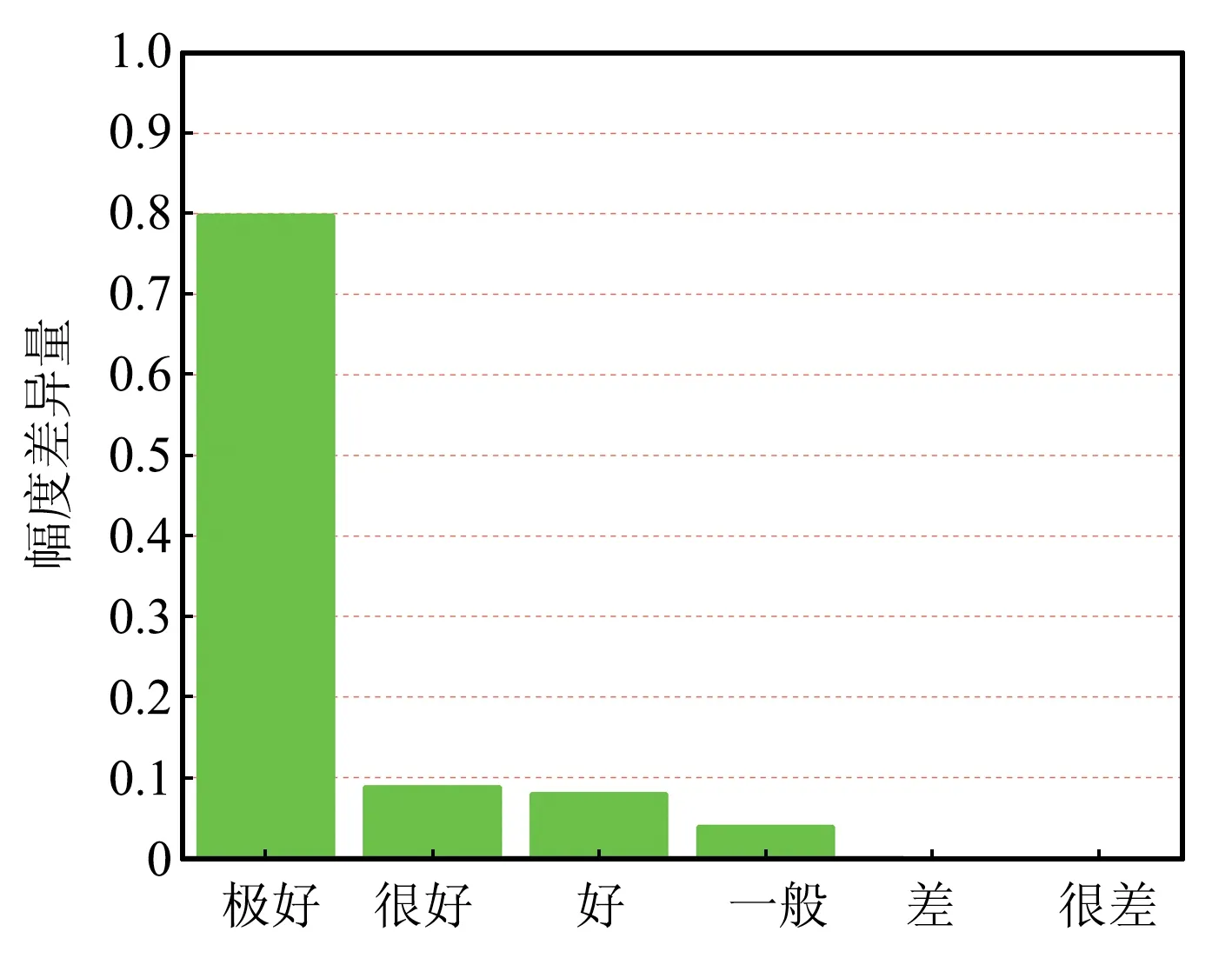
(a)BLT方程與CST仿真結果的ADM直方圖

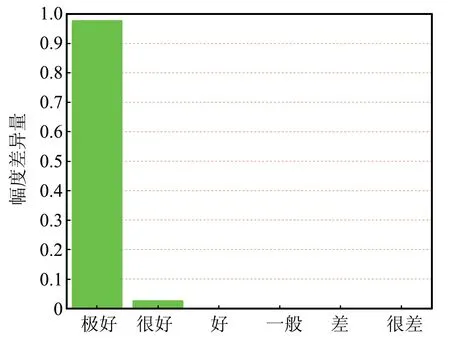
(b)時域混合算法與CST仿真結果的ADM直方圖圖4 3種方法計算得到的負載R2電壓的FSV評估Fig.4 FSV evaluation of the voltages of load R2 calculated by the three methods

由于BLT方程是一種頻域算法,對于寬頻帶串擾問題,需要重復多個頻點的計算以后,通過逆傅里葉變換得到負載電壓的時域響應,此過程需占用較多無用時間,因此未對BLT方程的計算時間進行統計。CST和時域混合算法計算所需網格量和時間的對比如表1所示,可以看出,在激勵源持續時間一致的情況下,時域混合算法的計算時間縮短為CST的1/16。原因是,雖然CST全波仿真使用自適應網格可以減少對PCB基板和微帶線精細結構的剖分網格量,但是時域混合算法只需對微帶線沿線劃分網格,且無需對基板結構直接建模,相較于CST,節省了大量的網格量而大大降低了內存需求和計算時間。

表1 時域混合算法與CST所需網格量和時間的對比Tab.1 Comparison of the grid number and cost time required by the time domain hybrid method and CST

為進一步驗證時域混合算法的置信度,將其應用于復雜T型微帶線級聯網絡的傳導干擾分析,對應的T型微帶線網絡的傳導干擾模型如圖5所示,整體網絡按照3個連接節點,可以分解為7段直微帶線,標記為#1～#7。介質基板和集總電壓源的參數設置均與上述算例相同。微帶線#2、#4的長度分別為2、6 cm,其余微帶線的長度均為3 cm。網絡端接負載為R1=R2=R3=R4=50 Ω。

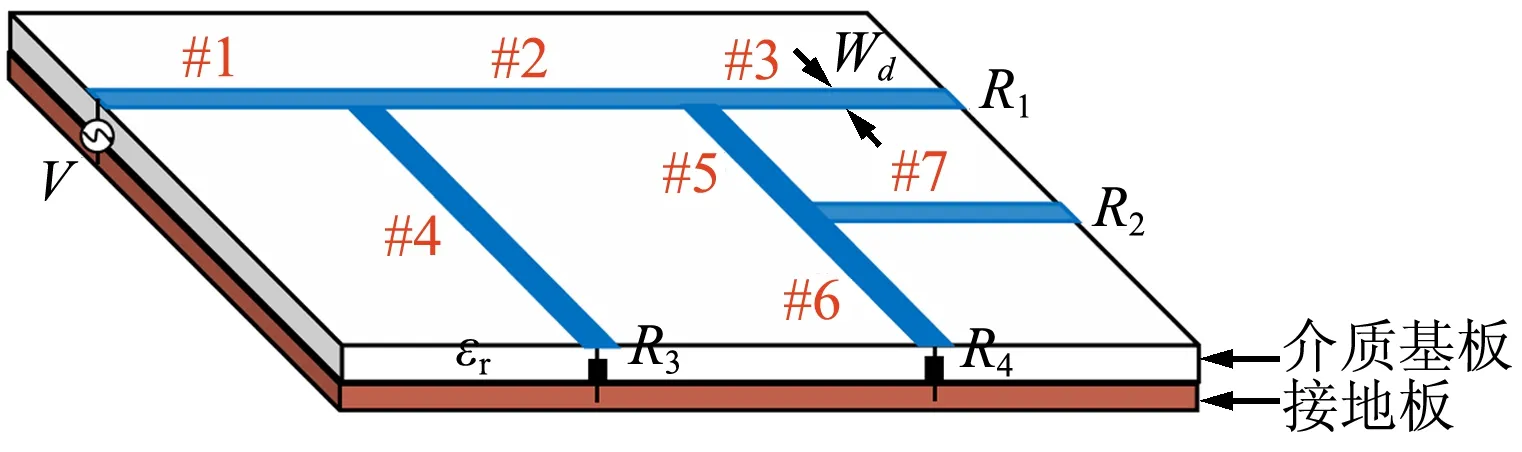
圖5 T型微帶線級聯網絡的傳導干擾模型Fig.5 Conducted interference model of T-shaped microstrip line cascade network

時域混合方法和CST計算得到的負載R2和R3上的電壓響應如圖6所示,同樣,采用FSV方法對2種方法的仿真結果進行幅度差異評估,得到對應的ADM直方圖如圖7所示。可以看出,2種方法的計算結果在幅值吻合度上達到很好以上等級的占比仍能保持100%。

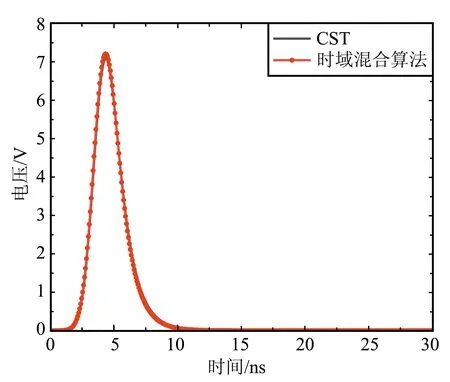
(a)R2上的電壓

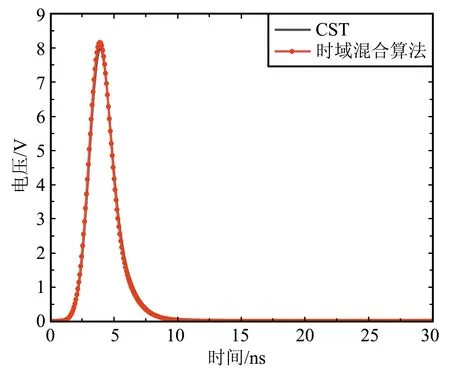
(b)R3上的電壓圖6 T型微帶線網絡不同負載的電壓響應Fig.6 Voltage responses on different loads of T-shaped microstrip line network

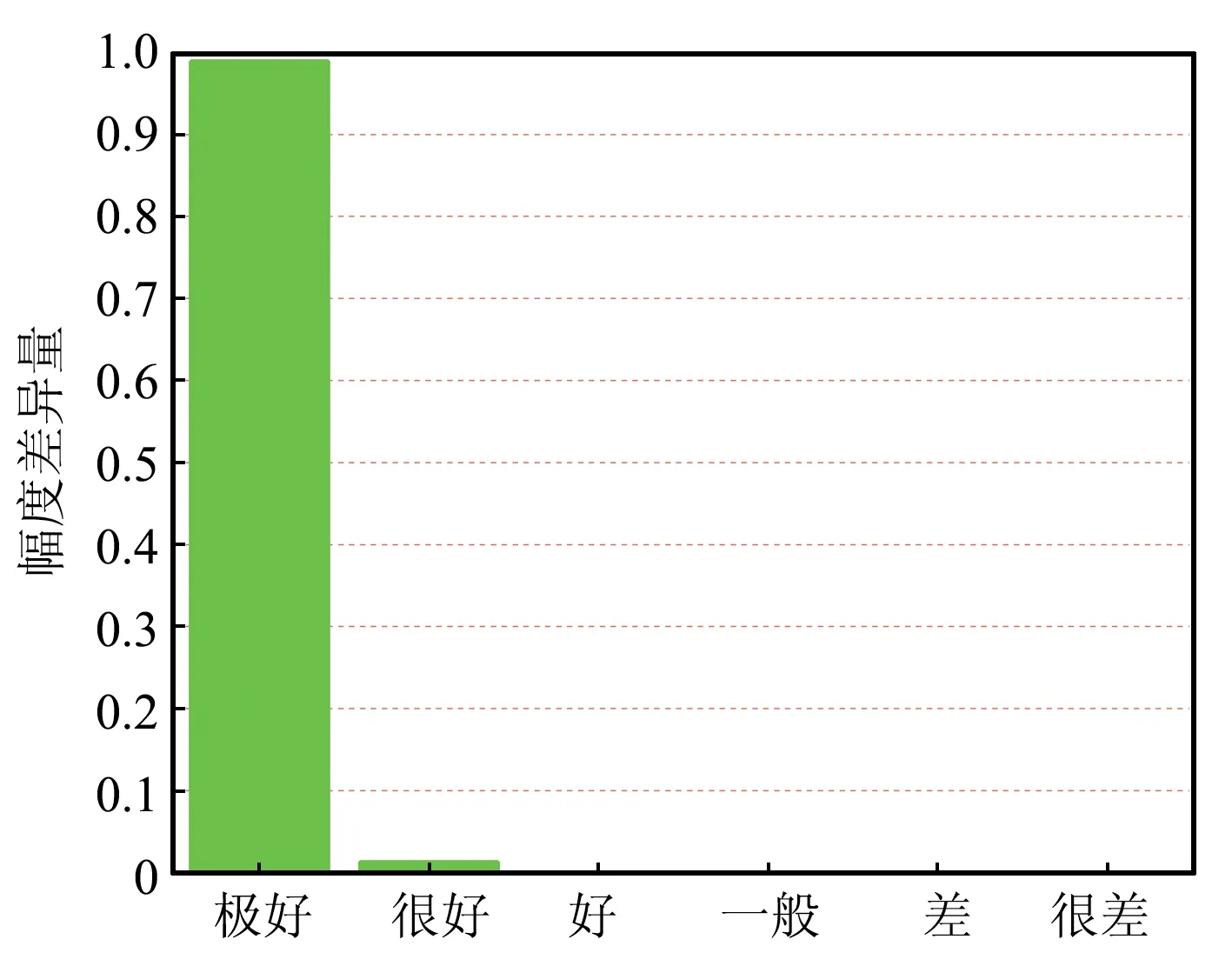
(a)R2上電壓的ADM

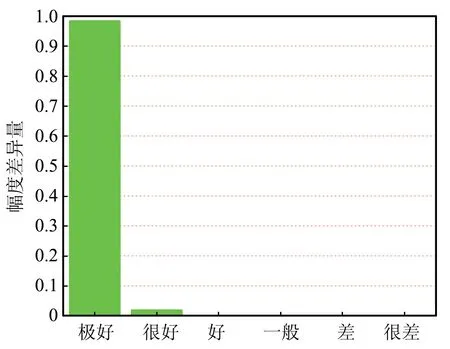
(b)R3上電壓的ADM圖7 T型微帶線網絡不同負載電壓的FSV評估Fig.7 FSV evaluation of the voltages on different loads of T-shaped microstrip line network

3 結束語

針對集成電路上T型微帶線的傳導干擾,將傳輸線方程與高階FDTD(2,4)和電荷守恒定律相結合,研究了一種高效的時域混合算法。該方法將T型微帶線分解成多段直微帶線和連接節點,采用傳輸線方程結合高階FDTD(2,4)快速求解各段直微帶線的傳導干擾響應,并在連接節點處應用電荷守恒,求解節點處的電壓響應。該時域混合算法能夠與CST全波仿真保持相同的計算精度,而且無需對T型微帶線的精細結構直接建模,使用高階FDTD(2,4)的大空間步長進行迭代求解,相較于全波算法可以節省大量計算時間。