金屬鎂非共面位錯相互作用強度的位錯動力學模擬

李賽毅，張磊，楊繼翔

(1. 中南大學 材料科學與工程學院，湖南 長沙，410083；2. 中南大學 有色金屬材料科學與工程教育部重點實驗室，湖南 長沙，410083)

金屬材料的應變硬化除了位錯滑移導致的自硬化之外，還存在不同滑移系位錯相互作用所引起的潛硬化。準確描述位錯相互作用是構建單晶硬化模型的重要基礎[1-2]。為了區分不同滑移系的潛硬化差異并體現其共同貢獻，人們對經典Taylor硬化方程進行了擴展[3-7]。

近年來，位錯動力學(dislocation dynamics，DD)的發展為探索位錯相互作用強度及其機理提供了新途徑[8-9]。該方法可以模擬外力作用下特定主位錯穿過隨機分布林位錯的集體運動，獲得特定應變水平或一定應變范圍內主滑移系的剪切應力τc，利用Taylor 類方程進行潛硬化分析。目前，基于DD模擬的潛硬化分析已被較多應用于面心立方(fcc)結構金屬[10-12]以及高溫下體心立方(bcc)結構金屬[6,12]，所得潛硬化系數亦逐步成為多尺度晶體塑性模擬的基礎數據[2,7,13-14]。這些研究在DD模擬及潛硬化分析時均忽略晶格阻力。對于密排六方(hcp)結構金屬，晶格阻力在流變應力中所占比例遠高于立方結構金屬，相應的位錯相互作用分析需要切實考慮其影響。而且，由于hcp結構金屬不同滑移系的位錯晶格阻力和運動性質存在顯著差異，位錯相互作用比立方結構金屬更加多樣化[15]。目前，僅有少數研究開展了hcp結構材料相互作用強度的計算分析[7,16]。BERTIN 等[7]考察了金屬Mg的基面、柱面位錯和二階錐面位錯在位錯密度ρf為1012m-2下的非共面相互作用。DEVINCRE[16]考察了冰(近hcp結構)的基面、柱面、一階錐面位錯在位錯密度為1012m-2下的非共面相互作用，但忽略位錯的晶格阻力且假設所有位錯具有相同的運動性質，不能充分體現不同滑移機制的差異。對于Mg，尚無關于一階錐面位錯參與下位錯相互作用強度的報道。因此，本文作者考慮Mg 的基面、柱面及一階錐面位錯滑移機制，利用DD模擬每對滑移系之間的非共面位錯相互作用，結合基于擴展Taylor方程的潛硬化分析以及模擬得到的位錯組態特征，探討不同相互作用強度的各向異性及其機理。

1 方法

1.1 滑移機制與位錯動力學方程

根據FRANCIOSI 等[4]的研究，主滑移系(p)位錯運動的臨界分解剪切應力(CRSS)τcp與不同林滑移系(s)上的位錯密度ρsf的關系可表示為

式中：τ0p為摩擦阻力，即林位錯密度ρsf=0 時主滑移系的CRSS，對于純金屬，τ0p為晶格阻力τFp；μp及bp分別為主滑移系的剪切模量及柏氏矢量大小；αps為表征滑移系p和s之間相互作用強度的系數，即相互作用系數。當p≠s時，αps為潛硬化系數。對于特定主位錯-林位錯相互作用(忽略變量上標p、s)，式(1)可改寫為與經典Taylor 硬化方程類似的形式：

潛硬化系數原則上可以通過單晶潛硬化實驗測定。但是，由于特定滑移系的精準加載以及位錯密度的準確測定較為困難，難以保證所得系數的精度，不同研究的結果也往往存在顯著差異[5-7]。

本研究考察基面、柱面及一階錐面位錯的非共面相互作用。各滑移系在四軸坐標系{ai，aj，ak，c}下的指數見表1。上述滑移機制可能產生的非共面相互作用共15 種，見表2。根據Frank 能量準則[17]，共線位錯反應可導致位錯湮滅，而非共線位錯反應可形成位錯交結。其中，有基面參與的非共線作用形成可動交結(即反應后生成的位錯片段在至少一個滑移面上可動)，而其他非共線作用則形成固著交結(即反應后生成的位錯片段在兩個滑移面上都不可動)。需要說明的是，這些判斷是僅考慮位錯反應的彈性能變化，而DD模擬得到的位錯組態是進一步考慮外力與晶格阻力的影響以及實際位錯線方向的結果。此外，由于自相互作用、共面相互作用的行為及機理與非共面作用存在較大差異[7,18]，本研究暫不考慮。

表1 本研究考慮的滑移系Table 1 Slip systems considered in the present study

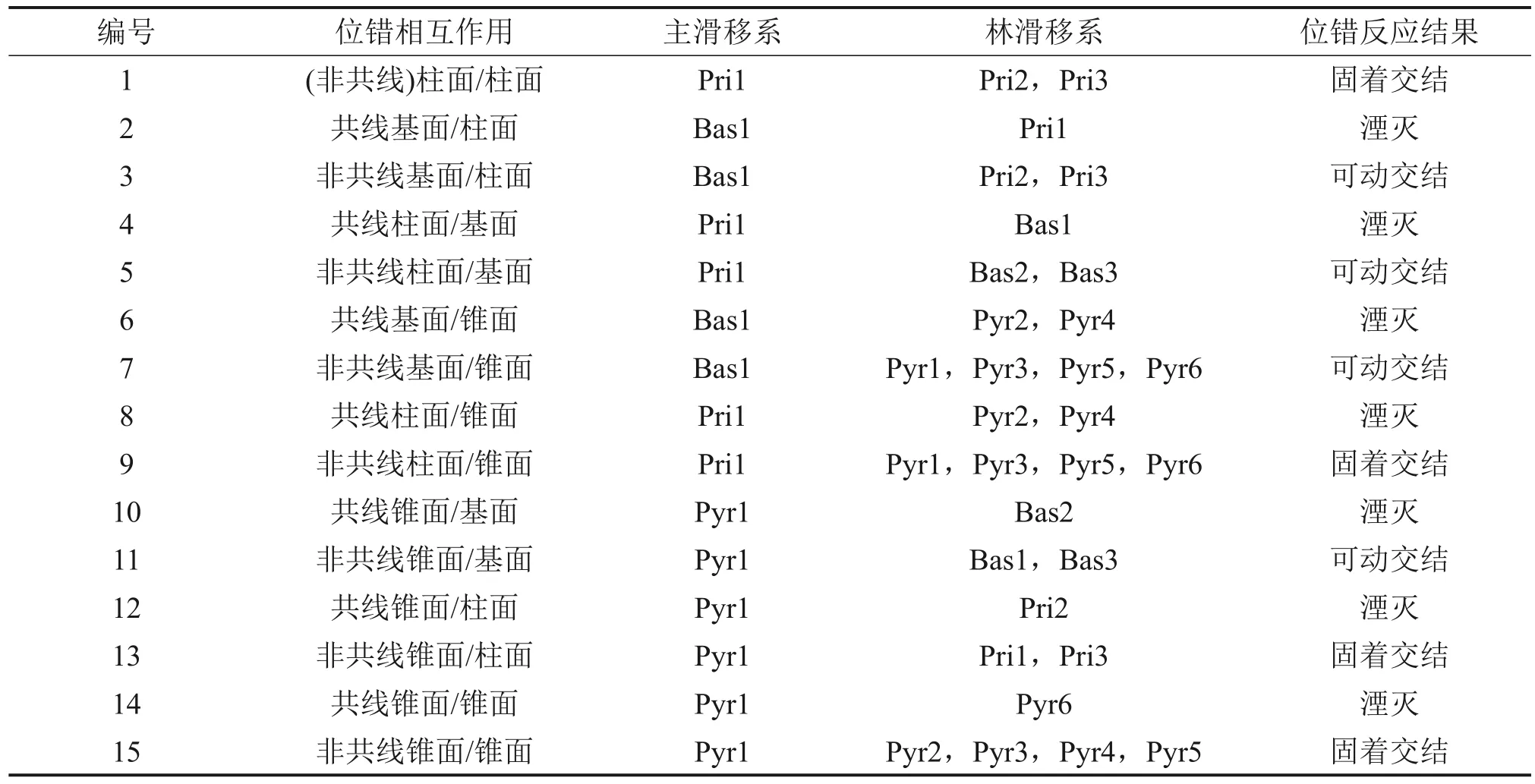
表2 位錯相互作用的滑移系設定及基于Frank能量準則的位錯反應特征Table 2 Slip systems involved in dislocation interactions and outcome of dislocation reaction according to Frank's energy criterion

DD模擬假設滑移系上位錯的運動符合黏滯拖拽(viscous drag)機制。每個位錯的運動速度v與其所受有效分解剪切應力τeff的關系為[8]

式中：τtot和Bd分別為位錯片段總受力所致分解剪切應力和表征位錯可動性的拖拽系數。

各類位錯的晶格阻力τF與拖拽系數Bd取值見表3，其中，基面和柱面位錯的τF取實驗值[19-20]，一階錐面的τF取試驗值[21]；除一階錐面螺位錯外，其他位錯的Bd均為分子動力學模擬結果[22]，而一階錐面螺位錯的Bd則依據基面與一階錐面刃位錯值之比等于螺位錯的Bd之比而推算得到。可以看出，各類滑移系的τF、Bd存在顯著差異。此外，材料彈性性能近似處理為各向同性，剪切模量μ=16.39 GPa，泊松比ν=0.34，柏氏矢量b=0.321 nm。

表3 位錯晶格阻力與拖拽系數Table 3 Lattice friction and drag coefficient of dislocations

1.2 建模計算

采用pure-mixed 位錯離散模式的DD 模擬軟件microMegas[8]，從微觀尺度模擬滑移系之間各類位錯相互作用。對于特定主、林滑移系，模擬在恒定應變速率條件下主滑移系的位錯滑移并穿過一定密度的林位錯的過程。模型基于正交坐標系{x，y，z}構建，晶體的c軸與正交坐標系中的[111]方向平行、3 個a軸則分別與正交坐標系中的3 個1/2<011ˉ>方向平行。{ai，aj，ak，c}至{x，y，z}的坐標轉換方法見文獻[23-24]。模型長×寬×高為5 μm×4 μm×6 μm，采用周期性邊界條件。

主滑移系上的位錯通過外加單軸拉伸應力驅動，相應的Schmid因子約為0.385，林滑移系上的Schmid因子則設為0，以防止位錯增殖。主位錯初始密度ρp=0.5×1012m-2，由兩端釘扎的刃型Frank-Read 源片段組成。林位錯初始密度ρf=1×1012m-2，由刃、螺及混合位錯源隨機生成。參考已有關于位錯片段長度等參數對相互作用強度影響的前期研究[6,24]，設主位錯平均長度Lp=6 μm、林位錯平均長度Lf=4 μm、應變速率=100 s-1、時間步長Δt=1 ns。利用擴展Taylor方程(式(2))并設τ0=τF，基于模擬得到的τc和ρf計算潛硬化系數α的瞬時值，并取剪切應變γ=0.1%～0.2%內的平均值。用于位錯組態分析的主位錯平均長度Lp、交結數量Nj、交結長度Lj等均取上述應變范圍內的平均值。為減小位錯空間分布可能產生的影響，每種相互作用均采用4 種不同初始位錯構型重復模擬，結果取平均值。

2 結果與討論

2.1 相互作用強度及其各向異性

圖1 所示為DD 模擬得到的主滑移系分別為基面、柱面及錐面滑移的各種位錯相互作用下的典型剪切應力-應變(τ-γ)曲線。從圖1 可以看出，所有曲線都表現出初始階段τ隨γ的增大而顯著提高，達到峰值后逐漸趨于相對穩定。在模擬統計數據對應的應變范圍內(γ=0.1%～0.2%)，τ已明顯離開峰值階段并開始進入相對穩態階段。除初始上升階段外，τ表現出較為明顯的鋸齒狀波動，是微觀層次位錯集體運動受到間歇性阻礙的結果。相對于各自主位錯晶格阻力，每種相互作用下準穩態階段的應力增長(即潛硬化水平)存在較為明顯的差異，介于0.5～4.0 MPa之間。

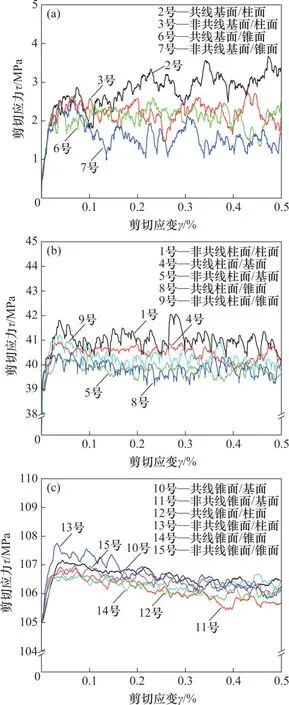
圖1 不同位錯相互作用下的典型主滑移系剪切應力-應變曲線Fig. 1 Typical shear stress-shear strain curves simulated for different dislocation interactions

不同位錯相互作用的強度比較如圖2所示，從圖2可以看出，不同位錯相互作用的強度存在顯著差異。共線基面/柱面(2號)及共線錐面/柱面(10號)相互作用最強(α=0.43、0.42)，非共線柱面/基面(5號)、共線柱面/錐面(8 號)相互作用最弱(α=0.11、0.12)。其次，考察相同主滑移系位錯相互作用的平均值發現，基面、錐面分別作為主滑移系的相互作用強度相當(約為0.31)，略高于柱面主滑移的相互作用強度(約為0.22)。這意味著，盡管基面滑移的CRSS初始值最小，但在變形過程中可能因潛硬化率較高而逐漸超過柱面滑移，從而導致后者在后續變形時更容易啟動。另外，潛硬化系數隨主、林滑移系的交換而變化，表現出不同程度的非對稱性。其中，最為顯著的是基面與柱面之間的非共線相互作用(3號、5號)、柱面與錐面之間的共線相互作用(8 號、12 號)。該特征與不同滑移系位錯幾何及運動性質差異有關，在涉及多種滑移機制的其他材料中亦存在，包括hcp 結構材料[7,16]和考慮{110}+{112}<111>滑移的bcc結構金屬[12]。

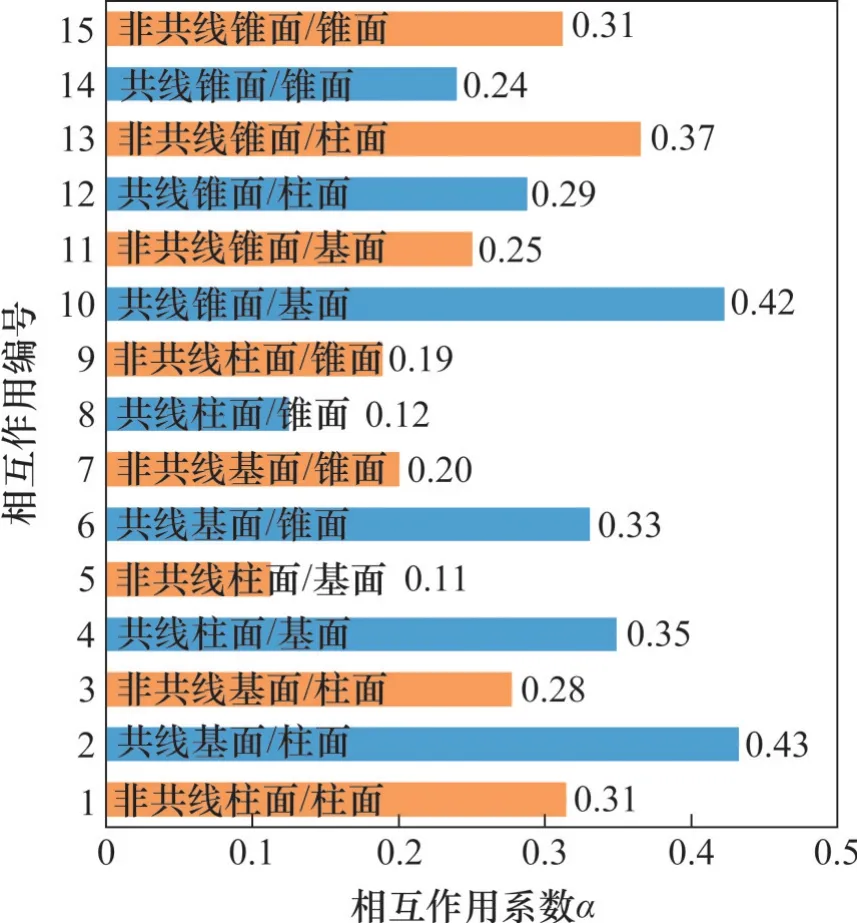
圖2 不同位錯相互作用的強度比較Fig. 2 Comparison of strengths in different dislocation interactions

目前，僅有少量研究報道了通過Mg單晶實驗得到的α。LAVRENTEV等[3]得到非共線基面/柱面相互作用下α=1，遠高于本研究模擬得到的結果(3號，α=0.28，見圖2)。需要說明的是，該實驗并非標準的潛硬化實驗，所得到的α可能包含了基面位錯共面相互作用對潛硬化的貢獻。而且，該實驗值對應的ρf(2×1010～12×1010m-2)比本研究獲得的ρf低一個數量級。根據大量fcc 結構金屬實驗結果分析及理論研究[18,25-27]，由于ρf對位錯線張力的影響，α隨ρf的增大而減小。為了檢驗此影響，采用與實驗較為接近的ρf(1011m-2)，重復模擬該相互作用，得到α=0.33，與實驗值差異縮小。因此，上述實驗值與計算值的差異還可能與ρf的差異有關。此外，GRAFF 等[28]通過晶體塑性模擬擬合平面應變壓縮試驗的應力-應變曲線，得到柱面/柱面相互作用的α為0.2，略小于本研究的系數(1 號，α=0.31，見圖2)。

2.2 共線與非共線相互作用的相對強弱

關于多種fcc 和bcc 結構金屬的研究表明，位錯的共線相互作用顯著強于非共線相互作用[10,12,18]。該發現突破了應變硬化完全由位錯交結性質主導這一傳統認識，是DD模擬的代表性成果之一[10]。基于本研究涉及的7組位錯相互作用，可以較為系統地檢驗hcp結構材料的共線與非共線的相對強弱。由圖2可以看出，共線與非共線相互作用的強弱關系隨滑移系而變化，只有基面位錯參與的相互作用對(2 號與3 號、4 號與5 號、6 號與7號、10 號與11 號)表現出共線作用強于非共線作用，而其他組別(8 號與9 號、12 號與13 號、14 號與15號)則相反。若考慮所有相互作用對，則共線作用強度比非共線作用強度平均高28%。由此看來，Mg的共線與非共線作用強弱關系比立方結構金屬更復雜。

目前，關于hcp結構材料共線與非共線相互作用相對強弱的討論較少。BERTIN等[7]基于ρf=1012m-2下的DD 模擬，借助擴展Taylor 式計算Mg 的基面和柱面、二階錐面位錯之間各種相互作用的潛硬化系數(相當于本研究的α2)。他們發現基面/柱面(2 號與3 號)、柱面/基面(4號與5號)相互作用對也表現為共線作用更強，與本研究結果一致。由于該研究考察的其他相互作用均有二階錐面位錯參與，不存在嚴格意義上的共線相互作用，而且其引自文獻的二階錐面位錯性質實際上均為一階錐面位錯的性質，不適用于上述比較。另外，DEVINCRE[16]研究了近hcp 結構的冰在ρf=1012m-2情況下的基面、柱面、一階錐面位錯相互作用，發現所有相互作用對(不含本研究的錐面/錐面作用對，即14 號與15 號)均表現為共線作用更強，達到非共線作用強度的4～20 倍。也就是說，對于本研究發現非共線作用更強的相互作用對(8號與9號、12號與13號)，該研究得到的規律與本研究的相反。需要指出的是，該研究的模擬和潛硬化分析均忽略摩擦阻力且假設各類位錯的拖拽系數相同，本質上忽略了不同滑移系位錯摩擦阻力及運動性質的差異，所得結果不能體現這些因素對位錯相互作用的影響。根據MONNET 等[29]的分析，提高τF會導致位錯間有效彈性相互作用距離減小，湮滅、交結長度減小，從而降低共線及非共線相互作用強度。因此，對于以τF較大的柱面(9 號)及錐面(13 號)作為主滑移系的相互作用對，DEVINCRE[16]的研究可能因忽略τF而改變了共線、非共線相互作用的相對強弱。

2.3 不同相互作用下的位錯組態

為探究共線與非共線作用相對強弱隨滑移機制而變化的原因，本研究考察了模擬得到的位錯組態。圖3所示為平行于主滑移面、厚度為0.5 μm的中心層處3組不同位錯相互作用形成的典型位錯組態。其中，基面/柱面相互作用(2 號與3 號)屬于共線強于非共線的代表(圖3(a)和(b))，錐面/柱面(12號與13號)相互作用(圖3(c)和(d))屬于共線弱于非共線且非共線作用下形成交結的情形，而錐面/錐面(14 號與15 號)相互作用(圖3(e)和(f))則是唯一表現為共線弱于非共線但非共線作用下沒有形成交結的相互作用。可以看出，所有的位錯共線相互作用由于主位錯與林位錯之間發生大量位錯湮滅反應而形成較短主位錯片段(圖3(a)、(c)、(e)，黑色實線圓圈處)，極少交結或無可見交結。非共線錐面/錐面(15號)作用沒有形成Frank能量準則所判斷的交結(圖3(f))，但其他非共線相互作用均形成大量交結(交結片段平行于兩滑移面交線)，且不同相互作用形成的交結長度及數量存在明顯差異(圖3(b)和(d))。上述共線作用下發生大量位錯湮滅以及非共線下形成大量交結的現象符合Frank能量準則的基本判斷(見表2)。

圖3 剪切應變約為0.1%時不同位錯相互作用形成的典型位錯組態Fig. 3 Typical dislocation configurations at γ=0.1% for representative dislocation interaction pairs

與其他非共線作用不同，非共線錐面/錐面相互作用(15)形成大量成交叉態(crossed state)的位錯(圖3(f)，黑色虛線圓圈處)。根據WICKHAM等[30-31]基于非共面位錯對之間短程彈性相互作用的計算，交叉態是當反應位錯相互吸引力不足以克服因合并成交結所致線張力變化時的另一種連結(bound)狀態，相當于形成“0 長度”交結。CAPOLUNGO[15]的分析進一步表明，當摩擦阻力較大時，相互吸引的位錯較難形成足夠長度(如：不小于10b)的交結，從而成為交叉態。本研究考察的錐面位錯的摩擦阻力顯著高于其他兩種機制下的摩擦阻力，因而更易形成交叉態。BERTIN等[7]在關于Mg 的非共線柱面/二階錐面作用模擬中亦發現類似交叉態位錯特征。圖4所示為非共線錐面/錐面相互作用下不同變形程度的位錯組態，顯示交叉態的形成與解除的典型過程，結果取自平行于主滑移面、厚度為0.5 μm的中心層，圖中，A，B，C，D表示交叉態位置。對比圖4(a)和(b)可以看出，初始為直線狀的主位錯在γ=0.02%時先后在A、B處與林位錯片段相遇而形成交叉態，且主位錯在A處呈現被釘扎的非連續形狀變化。隨著變形程度增大至γ=0.04%，A處的交叉態解除，主位錯在B處被釘扎，同時在C、D處已形成新的交叉態(圖4(c))。當γ=0.06%時，C、D處對主位錯形成明顯釘扎(圖4(d))。對比圖4(d)和3(f)還可以看出，該主位錯片段在后續變形過程中克服C、D處的釘扎而發生較大范圍的滑移。

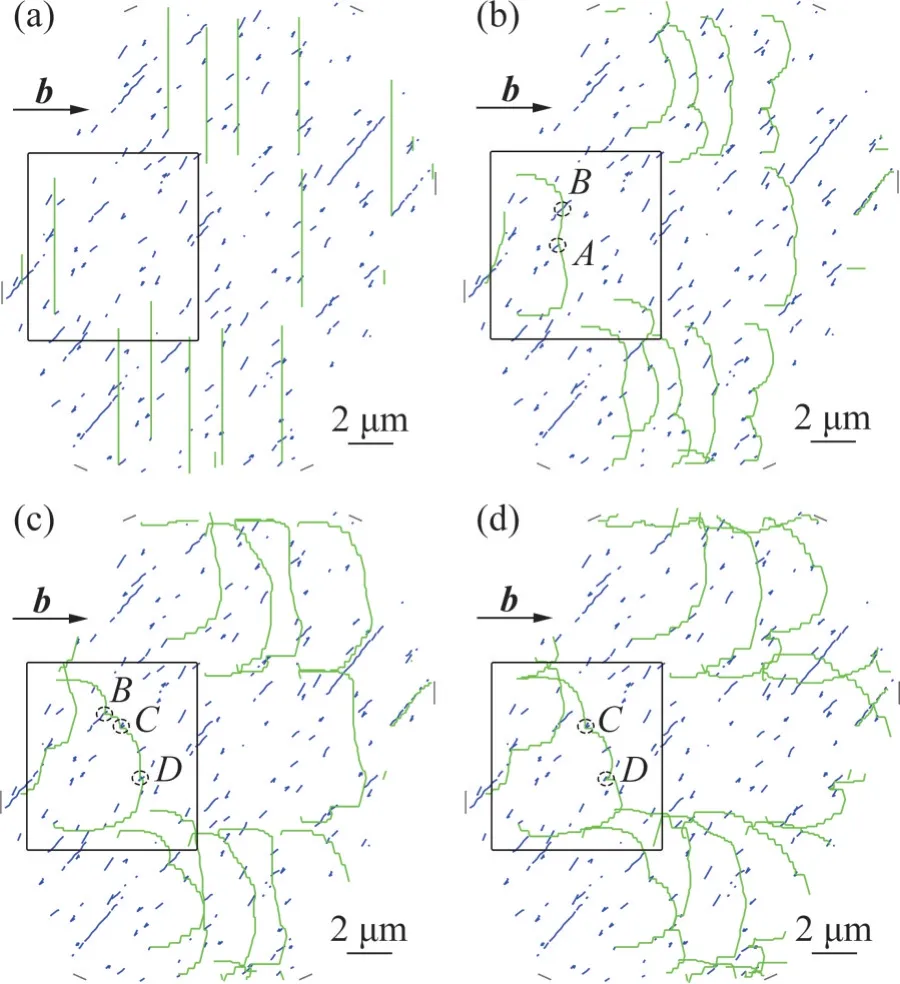
圖4 非共線錐面/錐面相互作用下交叉態的形成與演化Fig. 4 Formation and development of crossed states in non-collinear pyramidal/pyramidal dislocation interaction

為了系統分析共線與非共線相互作用相對強弱與位錯組態的關系，對比了7組共線和非共線位錯相互作用模擬得到的主位錯平均長度Lp，如圖5所示。圖6所示為所有非共線相互作用下的交結數量Nj和交結平均長度Lj。從這些統計結果可以進一步明確各種相互作用的位錯組態主要差異。除錐面/柱面共線與非共線相互作用(12 號、13 號)的Lp基本相同外，其他情況下共線作用的Lp均明顯小于非共線作用的Lp(圖5)。不同非共線作用下的Nj和Lj亦存在明顯差異。其中，形成可動交結的非共線作用(3號、5號、7號、11號)的Nj總體上明顯比形成固著交結的Nj高(1 號、9 號、13 號)(圖6(a))，但其Lj總體上略高于后者(圖6(b))。需要強調的是，非共線錐面/錐面相互作用(15 號)的Lp遠大于其他非共線作用的Lp，相應的交結數量為0。這是因為，該相互作用下主要的位錯反應是形成交叉態(圖4)，而目前的模擬將處于交叉態的位錯看成連續位錯，不計入交結數量的統計。

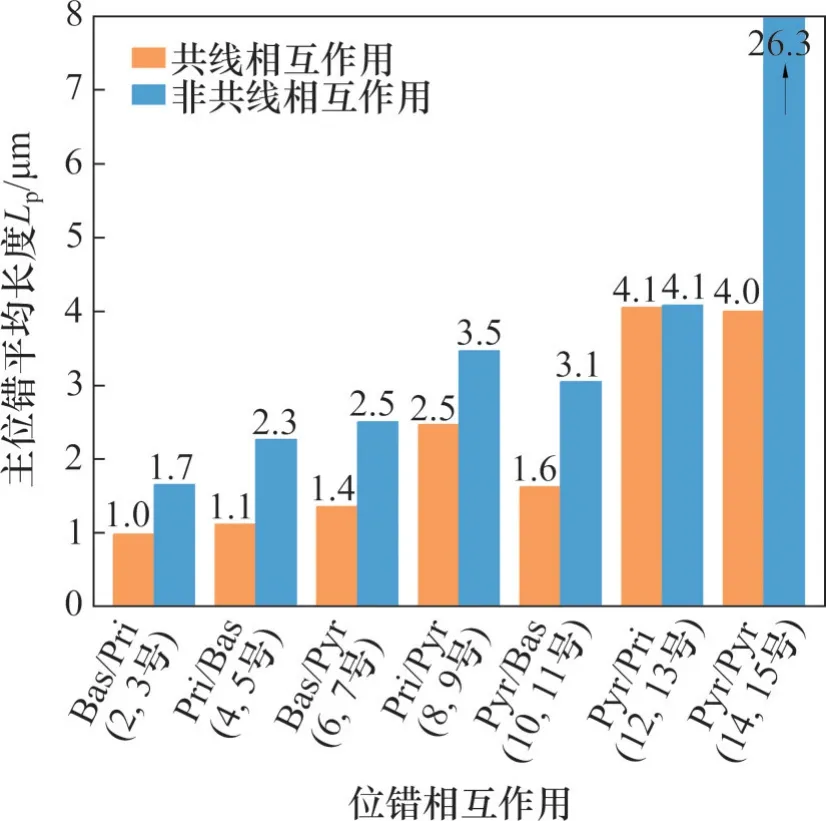
圖5 共線、非共線位錯相互作用模擬得到的主位錯平均長度比較Fig. 5 Comparison of average length of primary dislocations simulated for collinear and non-collinear dislocation interactions

圖6 不同非共線相互作用模擬得到的交結數量與平均長度Fig. 6 Number of junctions and average length of junctions simulated for non-collinear dislocation interactions

根據Frank-Read 位錯增殖機制，兩端受釘扎的位錯啟動所需應力與其長度成反比。相對于非共線作用，共線作用下的主位錯運動由于其Lj較小而需要克服更大阻力。同時，非共線作用下的位錯運動由于交結的阻礙而需要克服額外的阻力。因此，主位錯長度和交結數量兩方面的差異分別構成共線和非共線相互作用強度優勢，不足以解釋每組相互作用對的共線與非共線作用的相對強弱。但是，如表2所示，對于共線作用更強的相互作用對(2號與3號、4號與5號、6號與7號、10號與11號)，非共線作用形成的交結為可動交結，非共線作用更強的相互作用對(8 號與9 號、12 號與13號)則在非共線作用中形成固著交結。由于固著交結對主位錯運動的阻礙作用大于可動交結[1,4]，在其他位錯組態特征無系統性差異的情況下，可以推測固著交結對相互作用強度的總貢獻更大。以11號和13號非共線作用為例，前者交結數量和交結平均位錯長度均比后者的高，但強度比后者的低。另外，統計這6組相互作用對的潛硬化系數(圖2)發現，形成固著交結的非共線相互作用平均強度比形成可動交結的高約32%。這進一步佐證了固著交結對位錯運動更高的阻礙作用是導致部分相互作用對非共線作用強于共線作用的關鍵因素。若考慮交叉態是0長度的固著交結，則上述機理亦可以類似地解釋另一組非共線作用強于共線作用的作用對(14號與15號)。從圖4所示交叉態處的位錯形狀變化來看，非共線作用下主位錯運動在交叉態處受到類似于交結的阻礙作用。但是，如前所述，由于DD 模擬時交結判定方法的局限，含交叉態位錯組態的定量結果顯著不同于其他非共線作用，難以進行直接比較。

上述分析表明，Mg的不同相互作用對呈現相反的共線與非共線作用強弱關系，且與非共線條件下所形成的交結性質存在明顯相關性。該發現與fcc 和bcc 晶體的位錯相互作用顯著不同，后者尚無非共線相互作用強于共線作用的報道[10-12,18]。早期MADEC 等[10]對Cu 的DD 模擬研究得到共線相互作用強度為最強非共線作用強度的15倍左右。近期MADEC 等[12]對12 種fcc 和bcc 結構晶體的系統研究進一步表明，共線作用為最強非共線作用強度的4～5倍。這些研究存在一個共同點，即模擬及潛硬化分析都忽略摩擦阻力。對于摩擦阻力不應被忽略的hcp材料，不同滑移系的摩擦阻力存在顯著差異。該差異可能是導致相互作用強度隨滑移系而顯著變化，以及部分相互作用對出現非共線作用強于共線現象的重要原因。

3 結論

1) 根據擴展Taylor方程所算潛硬化系數，不同位錯相互作用的強度存在顯著差異，且表現出明顯非對稱性。共線基面/柱面相互作用最強(α=0.43)，非共線柱面/基面最弱(α=0.11)。

2) 共線相互作用下主位錯長度由于位錯湮滅明顯小于非共線相互作用主位錯長度，非共線作用下則形成大量位錯交結或交叉態位錯。形成固著交結的非共線相互作用平均強度顯著高于形成可動交結的非共線相互作用。

3) 不同于fcc及bcc結構晶體，Mg的特定位錯相互作用對的共線與非共線作用強弱關系隨滑移機制而變化，主要與非共線作用下所形成交結的性質有關。