鐵氧體磁芯磁場分布的優化及其對磁納米熱療的影響

湯云東，陳泓霖，高躍明

(福州大學 物理與信息工程學院，福建 福州，350108)

磁納米熱療相比傳統熱療方法具有毒副作用低、靶向性好、對生物體影響較小等優點，已成為近年來最有潛力的腫瘤治療手段之一[1-2]。此外，磁熱療還可以作為輔助手段與其他常規治療方式，如化療、藥物治療及免疫療法等[3-5]進行聯合最終提高治療效果。磁熱療的基本原理是在外加交變磁場的作用下，注入腫瘤區域內的磁納米粒子(magnetic nanoparticles, MNPs)產熱，致使癌細胞因高熱敏感性凋亡同時不損傷健康組織的治療方法[6-8]。因此，治療溫度的有效控制是磁熱療最為關鍵的環節，而理想的治療溫度一般為42～46 ℃[9]。磁熱療期間治療溫度的決定性因素主要包括磁場和生物組織的特性、含MNPs的磁流體屬性參數以及磁流體的注射策略等[10]。盡管以往的文獻已經從不同方面對磁熱療進行了闡述，但治療磁場的優化問題并未得到國內外學者較多的關注。

目前，用于產生磁熱療所需的交變磁場裝置一般有通電螺線管[11]、亥姆霍茲線圈[12]以及纏繞載流線圈的鐵氧體磁芯。理想情況下的治療磁場應為均勻分布，但實際裝置的磁場多為不均勻分布，而不均勻分布磁場會大大地影響磁熱療過程中的治療效果[13]。為此，國內外學者不斷地嘗試改進磁場裝置以期獲得理想的磁場發生裝置。RISTI?-DJUROVI? 等[14]為克服典型螺線管磁場均勻性較差的缺點，通過改變螺線管橫截面的形狀和尺寸從而減小磁場的變化，優化后的螺線管幾何結構可實現最大的現場性能和最小的功耗，而且可保證獲得最大磁感應強度時擴展螺線管尺寸，所提出的修改方法可將磁場均勻度變化減少10.6倍。LU等[15]則應用改進的3-s和四線圈結構對亥姆霍茲線圈體積均勻場進行優化，并通過有限元分析驗證了所提歸一化線圈參數公式的準確性，還通過實驗驗證了理論分析，揭示了改進后線圈可使功率損耗和導體質量顯著下降，其性能也明顯優于傳統線圈。CHRISTIANSEN 等[16]提出一種小型交變磁場裝置方案，該方案使用軟鐵磁芯將磁通集中到間隙中。然而，隨著用于適應動物模型的實驗空間增加，該裝置的導熱性變差，體積標度的堆芯損耗增加。盡管該裝置也具有較好的應用前景，但研究中并未對這種裝置提出有效的優化方法。NOMURA等[17]考慮鐵氧體磁芯在產生磁場時由于渦流損耗、趨膚效應和鄰近效應而造成的繞組損耗和磁芯損耗，并對磁體的熱損失進行了評估，同時給出了熱療磁場裝置可行性系統的主要參數。王世山等[18]推導了兩類磁場在各自自由度下滿足的微分方程，進而采用類比有限元法計算出鐵氧體磁芯磁場的特征參數，求解了磁芯的等效電感和電阻等。盡管以往文獻對各種裝置磁場進行相應研究，但針對鐵氧體磁芯磁場的優化和改進工作并沒有獲得足夠的關注，而基于優化磁芯磁場的磁熱療研究仍需進一步探究。

因此，本文應用遺傳算法對鐵氧體磁芯的氣隙長度和寬度等進行優化，使得氣隙內磁場均勻度最優的同時保證磁場強度能讓治療溫度處于臨界值；進而采用有限元方法求解氣隙磁場的偏微分方程，對磁芯線圈的位置進行優化設計，分析線圈處于不同位置時鐵氧體磁芯磁場的等效磁路模型；最后，將優化后的氣隙磁場應用于磁熱療的治療溫度模擬，并比較優化前后不同磁場對治療效果的影響，在考慮了相應的初始條件和邊界條件下，使用有限元方法對改進生物傳熱方程求解，預測生物組織治療溫度。

1 理論和方法

1.1 鐵氧體磁芯磁場

以常見的帶有載流線圈的鐵氧體磁芯作為磁熱療交變磁場發生裝置[16]。圖1所示為磁場發生裝置初始幾何模型，該模型主要包括帶氣隙結構的鐵氧體磁芯(藍色)和套在磁芯上的載流線圈(黃色)。其中，鐵氧體磁芯的高度為16 cm，寬度為12 cm，而磁芯上纏繞的線圈材料由金屬銅構成。

圖1 磁場發生裝置的初始幾何模型Fig. 1 Initial geometric model for magnetic field generator

鐵氧體磁芯上的線圈加載交變電流時，磁芯間隙中會產生相應的交變磁場，由麥克斯韋方程組可知：

式中，?為梯度算子；H為磁場強度；Ji為外加電流密度，可以認為是電磁場的來源；Jc為傳導電流密度；Jc=σE，σ為媒質的電導率；E為電場強度；D為電位移矢量，D=εE，ε為媒質的介質常數；B為磁感應強度，B=μ0H，μ0為真空磁導率。

此外，根據Maxwell Faraday 方程，靜止系統中的電場強度可以表示為

式中：A為磁矢勢；?為標量勢，在本模型中不考慮聚集電荷，故假設其值為0。

將式(2)和式(3)代入式(1)，并結合已知的關系式可以得到新的磁矢量勢方程：

通過求解方程(4)可得到磁矢勢A，并通過B=?×A求解得到磁感應強度B，再依據B=μ0H可得出鐵氧體磁芯內部和氣隙空間中的磁場強度。

1.2 磁場作用下MNPs的產熱

MNPs 置于鐵氧體磁芯氣隙中的交變磁場后，在交變磁場的作用下將產生用于腫瘤治療所需的熱量[19-20]。在粒徑較小的情況下，MNPs產生的功率主要由弛豫損耗所決定，可表示為[21-22]

式中：P為功率；f為交變磁場的頻率；χ″為復磁化率的虛部，

式中，ω為角頻率，ω=2πf；χ0為平衡磁化率；τeff為MNPs的弛豫時間，

式中：τB為布朗弛豫時間；τN為尼爾弛豫時間；η為磁流體的黏滯系數；VH為磁流體粒子的流體動力學體積；kb為玻爾茲曼常數；T為熱力學溫度；τ0為平均弛豫時間；參數γ=KeffVm/(kbT)，Keff為有效各向異性常數，Vm為MNPs 的體積，Vm=4πR3/3，R為MNPs的半徑。

平衡磁化率χ0可以由下式表示：

式中：ξ為朗之萬參數，ξ=μ0MdH0Vm/(kbT)，Md為磁性顆粒的磁化強度；χi為初始磁化率，

式中：Ms為MNPs 的飽和磁化強度，Ms=ΓMd，Γ為MNPs的體積分數。

確定MNPs的產熱情況后，生物組織的溫升變化則可通過Pennes bio-heat transfer(PBHT)方程來預測。本文考慮了一種改進的PBHT方程[23-25]：

式中：i的值為0或1，分別表示健康組織和腫瘤組織；ρi，ci和ki分別為生物組織的密度、比熱容和熱導率；ρb，cb和ωb分別為血液的密度、比熱容和灌注率；Tb為動脈血液溫度；Qm為生物組織代謝熱；α為校正系數，用于校正理論和實際情況下，不同溶液對MNPs產熱影響的差異，一般取為0.55；QMNP為在交流磁場作用下磁納米粒子在生物組織區域中產生的總熱量。

QMNP與磁納米粒子的空間濃度分布以及單個磁納米顆粒在交變磁場作用下產生的熱量有關，因此，QMNP=φ′(x,y,z)?P，式中，φ′(x,y,z)為體積分數，用于說明腫瘤組織區域內的磁納米粒子濃度分布。在本研究中，考慮腫瘤區域內的磁納米粒子濃度分布為高斯分布，則φ′(x,y,z)可以表示為

式中，σ0為磁納米粒子空間分布的方差，φ為磁納米粒子的初始體積分數，σ0和φ分別取為20 和0.071；(x0,y0,z0)為磁納米粒子的注入點，在本研究中定義為(0, 0, 0)。

1.3 鐵氧體磁芯磁場優化方法

與螺線管和亥姆霍茲線圈相比，鐵氧體磁芯產生的磁場容易實現相對較高的磁場強度，但同時也存在一定的不足[26]，主要表現在：鐵氧體工作時存在的磁滯損耗會引起鐵氧體溫度上升并增加額外的功耗；鐵氧體磁芯氣隙附近存在一定的磁通量分散，會導致氣隙中磁場強度下降和磁場分布不均勻，而這些均會影響MNPs的產熱，進而對熱療溫度場的分布造成影響。其中，磁滯損耗與鐵氧體中的磁通密度有關，而載流線圈位置則會影響鐵氧體中磁通密度以及氣隙中磁場強度。本文針對鐵氧體磁芯磁場提出的改進方法如下：首先，應用磁路理論分析載流線圈處于不同位置時的等效磁路模型，同時使用有限元軟件對不同的載流線圈位置進行仿真模擬；接著，對比仿真結果得出最佳的載流線圈位置后，將其應用到鐵氧體磁芯中；最后，利用優化算法去進一步優化確定后的鐵氧體磁芯氣隙磁場，使磁場分布均勻程度最優以提高磁熱療的有效性。

為此，本文提出了一個用于評價磁場均勻性優化問題的不均勻性函數[27]：

式中：Hmax、Hmin和Hmean分別為鐵氧體磁芯氣隙區磁場強度的最大值、最小值和平均值。

此外，為提高治療區域磁場的均勻性，采用遺傳算法對不均勻性函數進行優化，優化算法中的待優化參數包括氣隙兩側截面的鐵氧體磁芯的長度和寬度等[28-31]。值得一提的是，遺傳算法并不是本文研究的唯一可用算法，現有的諸多優化算法可能同樣適用。然而，本文重點并不是關注優化算法導致的差異，故此處不展開討論。

本文基于遺傳算法的鐵氧體磁芯磁場優化方法流程如圖2所示，優化步驟可概述如下：

圖2 優化過程流程圖Fig. 2 Flow chart for optimization process

1) 將要使用的氣隙兩側截面鐵氧體磁芯的長度和寬度視為優化過程中的變量，并對它們進行二進制編碼。每個變量的編碼長度為10 之后通過隨機函數在編碼長度內隨機生成0 或1，從而產生兩組隨機數作為算法中的初始群體；

2) 對群體中個體進行評價，包括對參數進行解碼以及根據解碼后的參數計算不均勻性函數F并保存；

3) 判斷不均勻性函數F的平均相對變化是否小于所設置的函數容差(本文函數容差設置為10-6)；

4) 若不滿足所設置函數容差要求，則對群體進行遺傳操作獲得新的參數并產生新一代的群體；并再一次重復步驟2)和步驟3)直到滿足函數容差要求，則算法停止迭代并結束優化。

優化算法迭代完成后將得到不均勻性函數F的最優值，同時得到最優化待優化參數(磁芯的長度和寬度)。同樣地，在最優待優化參數作用下，鐵氧體磁芯也將獲得最均勻的磁場分布，將該最優磁場應用于磁熱療時可在腫瘤區域獲得均勻的產熱分布。

2 生物組織參數

2.1 常量參數

為了求解方程(5)中的功率P，參考文獻[32-33]選取MNPs產熱相關的參數，如表1所示，為求解改進的PBHT 方程即式(11)，根據文獻[33]選取生物組織特性參數，如表2所示。

表1 MNPs產熱參數Table 1 Parameters for heat generation by MNPs

表2 生物組織特性參數Table 2 Parameters for bio-tissue characteristics

2.2 磁納米粒子注入后的熱特性

隨著MNPs的注入擴散，改進的PBHT方程中考慮的腫瘤參數應同時包含MNPs和腫瘤組織。因此，注射后腫瘤混合區的生物組織特性參數可通過以下計算方法來描述[34]：

式中：下標tumor 和MNP 分別表示腫瘤和磁納米粒子；ε為MNPs 注射進腫瘤區域后在該區域內所占的體積分數，其臨床典型值為0.003[35]。

2.3 溫度依賴性的血液灌注率

除了磁納米粒子的注入會對生物組織特性參數造成影響之外，治療期間溫度的變化也會對其造成影響，其中，血液灌注率會隨著局部溫度的變化而改變。因此，為了使所計算的溫度分布更加準確，本文將血液灌注率視為人體健康組織和腫瘤組織的局部溫度的函數，其表達式如下：

式中：ω0b(T)和ω1b(T)分別為健康組織和腫瘤組織中受局部溫度影響的血液灌注率。

3 結果和討論

3.1 載流線圈位置對于鐵氧體磁芯磁場的影響

鐵氧體磁芯磁場跟線圈位置以及氣隙特征等均相關，確定線圈的最優位置有利于氣隙特征的優化。圖3所示為線圈分別位于磁芯左端圖和氣隙兩端時的鐵氧體磁芯磁場模型。圖3中，帶隙的空心長方體表示磁芯，套在磁芯上的黃色圓環表示載流線圈，而氣隙中的同心球則表示生物組織，同心球中灰色區域表示人體健康組織(半徑150 mm)，綠色區域表示腫瘤組織(半徑100 mm)。

圖3 不同線圈位置時的鐵氧體磁芯磁場模型Fig. 3 Magnetic field model of ferrite core with different coil locations

運用磁路理論分析圖3可得到如圖4所示的磁路等效圖，其中，載流線圈用磁動勢表示，磁芯中各部分磁路用磁阻表示，NI?sin(ωt)為線圈中的磁動勢，Rg為氣隙中的磁阻，Rl為磁芯上下兩端之間的磁阻，Rm為磁芯左端的磁阻，Rl>Rg?Rm。圖4(a)中，Rg與Rl并聯后再與Rm串聯，故總磁阻可表示為Rm+Rl//Rg，圖4(b)中，Rg直接與線圈相連，故總磁阻可等效為Rg+Rl//Rm。因此，2 種情況下的總磁阻并不相同，這也將導致磁芯中磁通密度分布以及氣隙中的磁場強度不同。

圖4 不同線圈位置時的等效磁路圖Fig. 4 Equivalent magnetic circuit diagram with different coil locations

利用有限元方法對式(4)進行求解后，可得到相同電流下不同線圈位置時鐵氧體磁芯磁場的分布，如圖5所示。由圖5可知：線圈位于氣隙兩端時的磁通密度比位于磁芯左端時的磁通密度更低，導致其磁滯損耗也更小；線圈位于氣隙兩端時的磁場強度比位于左端時的磁場強度更大，而這兩者的差異見圖5(e)，其中，L1表示圖5(c)對應的曲線，而L2 表示圖5(d)對應的曲線。這也表明產生相同的磁場強度，線圈位于氣隙兩端時所需的功率會更小。因此，線圈在氣隙兩端優于在磁芯左端，能產生更有利于磁熱療所求的交變磁場。

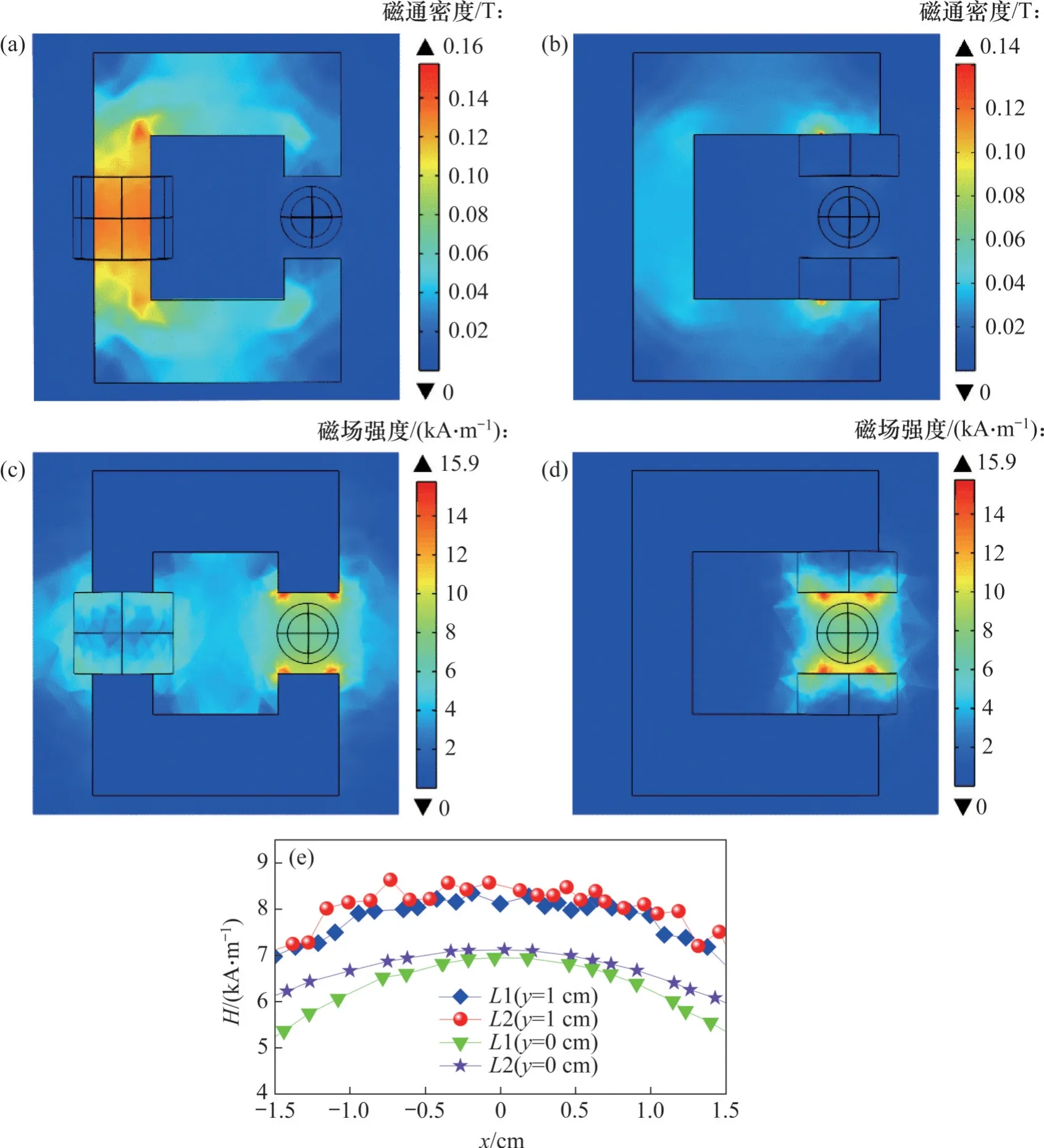
圖5 不同線圈位置的磁芯磁場分布Fig. 5 Magnetic field distribution for magnetic core with different coil locations

盡管如此，由圖5(d)可知，氣隙中磁場強度分布的均勻度并不理想，故本文采用遺傳算法通過優化鐵氧體磁芯多個參數來提高氣隙中磁場強度分布的均勻度，從而提高磁熱療治療的溫度分布以及治療效果。

3.2 鐵氧體磁芯磁場的優化

鐵氧體磁芯磁場的影響因素較多，主要包括磁導率、飽和磁通密度、電阻率、剩余磁通密度、矯頑力以及磁芯幾何尺寸等。其中，磁導率和飽和磁通密度會影響鐵氧體磁芯工作時產生的磁感應強度幅值，而電阻率、剩余磁通密度以及矯頑力則與鐵氧體磁芯在磁化時所造成的能量損失有關。然而，本文主要關注氣隙內磁場強度的均勻性，其與上述參數關聯性并不大，但與鐵氧體磁芯截面的長度和寬度密切相關。鑒于此，本文最終確定鐵氧體磁芯截面的長度和寬度為遺傳算法的優化參數，以線圈位于氣隙兩端情況為分析對象，采用本文所提優化方法對氣隙兩端參數進行優化，以期提高磁熱療裝置的氣隙磁場均勻性。

利用本文所提優化方法進行優化過程中，迭代變量和不均勻性函數F的收斂曲線如圖6 所示，其中，圖6(a)中的2個待優化變量分別為氣隙兩端對應的鐵氧體磁芯截面的寬度(w)和長度(l)。從圖6可以看出，在迭代400次前，迭代變量和不均勻性函數均出現較大的波動，而在迭代400次后，兩者開始穩定并一直保持不變。且在收斂后不均勻性函數值從開始的0.8下降到了0.2左右。

圖6 迭代變量和不均勻性函數的收斂曲線Fig. 6 Convergence curve of iterative variables and inhomogeneity function

確定最優參數后，鐵氧體磁芯氣隙中的磁場分布便可通過求解有限元方程(4)獲得。

圖7 所示為優化后氣隙中磁場強度分布在x-y平面的切片圖(z=0)。由圖7可以看出，優化后，氣隙中磁場強度分布的均勻度得到顯著提高，特別是在氣隙邊緣區域優化尤其明顯。為進一步闡明優化效果，圖8 所示為優化前后氣隙中不同位置x軸截線的磁場強度變化曲線。由圖8(a)可知，氣隙區域內優化前磁場強度最大值在9 kA/m 左右，而最小值則在5.5 kA/m 左右，兩者相差達3.5 kA/m；優化后，磁場強度最大值和最小值的差異減小到1.5 kA/m 以內，氣隙內磁場均勻度得到明顯提升。因此，也證明了本文所提優化方法的有效性。

圖7 優化后x-y平面磁場強度分布Fig. 7 Magnetic field intensity distribution in x-y plane after optimization

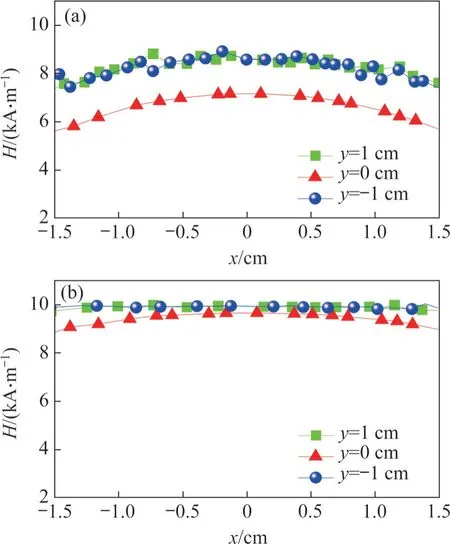
圖8 優化前后不同位置的x軸截線的磁場強度變化曲線Fig. 8 Magnetic field intensity curve for x-axis crosssection at different positions before and after optimization

3.3 優化前后磁場對于熱療溫度場的影響

氣隙內磁場優化完成后，通過求解方程(11)便可獲得生物組織的溫度分布。磁熱療過程中，合適的治療溫度范圍(42～46 ℃)可以使癌細胞凋亡同時不損傷健康組織，本文以腫瘤區域內有效溫度體積百分比(effective temperature percentage inside tumor, ETPIT)來評估治療效果。圖9所示為相同電流下不同磁場作用下生物組織區域的穩態治療溫度分布結果。由圖9可知，優化后磁場下，治療溫度整體上升，其治療區域最高溫度從未優化磁場下的44.5 ℃升至46 ℃，整體治療溫度顯著上升，同時，評估參數ETPIT 也從46.76%升至優化后磁場下的88.95%。

圖9 生物組織區域的治療溫度分布Fig. 9 Treatment temperature distribution for bio-tissue region

由式(11)可知，治療溫度最大值實際上主要取決于MNPs的產熱功率，因此，優化前的氣隙磁場分布通過對線圈電流進行窮舉法多次嘗試也可使得治療區域最大值指定為臨界治療溫度(46 ℃)。為了進一步揭示優化前后磁場均勻性對治療溫度分布影響的差異，本文應用窮舉法人為多次嘗試將線圈電流設定為10.8 A后，可獲得未優化磁場裝置下治療區域溫度最大值為46 ℃的組織溫度分布。盡管調整后未優化磁場和優化后磁場分別作用下的生物組織區域最高溫度相同，但這2種情況下的生物組織區域溫度分布必然不同。在最大值均為46 ℃時，調整后未優化磁場和優化后磁場作用下的生物組織治療溫度差異分布如圖10 所示。從圖10可以看出，2種情況下腫瘤中心治療溫度均為最大值46 ℃，即中心及附近的溫度差異基本為零。此外，隨著距中心距離的增加，兩者的溫度差異變得明顯，但沿著不同軸向并不對稱，這主要由氣隙內磁場的不對稱性決定。總之，優化磁場作用下治療溫度整體更高，最大差值可達到0.5 ℃，故其治療效果最佳。因此，本文所提氣隙內磁場優化方法不僅能提高磁場分布的均勻性，也能使得磁熱療期間治療溫度分布整體更優。

圖10 兩種不同磁場作用下的治療溫度差異Fig. 10 Temperature difference under two different magnetic fields

4 結論

1) 在鐵氧體磁芯磁場中，鐵氧體磁芯線圈位于氣隙兩端比位于磁芯左端更優。

2) 利用遺傳算法優化后，氣隙中磁場強度分布的均勻性明顯提高，氣隙區域內磁場強度最大最小值差異從優化前的3.5 kA/m 左右迅速減少至1.5 kA/m以內。

3) 腫瘤區域內有效溫度體積百分比從優化前的46.76%提高至88.95%，治療效果顯著提高。

4) 雖然通過窮舉法提高線圈電流方式來提高MNPs產熱值的方式可將有效治療溫度百分比也提高至79.82%，但總體的治療效果還是較本文所提優化方式差；本文所提優化方式在提高腫瘤組織內溫度分布均勻性(最大溫差為0.5 ℃)的同時，還在一定程度上降低了線圈的輸入電流。