重載列車作用下新型預(yù)應(yīng)力路基動(dòng)應(yīng)力響應(yīng)規(guī)律研究

董俊利，冷伍明,2，張期樹,3，徐方,2，聶如松,2

(1. 中南大學(xué) 土木工程學(xué)院，湖南 長(zhǎng)沙，410075；2. 中南大學(xué) 重載鐵路工程結(jié)構(gòu)教育部重點(diǎn)實(shí)驗(yàn)室，湖南 長(zhǎng)沙，410075；3. 中南林業(yè)科技大學(xué) 土木工程學(xué)院，湖南 長(zhǎng)沙，410004)

預(yù)應(yīng)力路基是一種新型鐵路路基結(jié)構(gòu)形式，它既適用于新建線建設(shè)，也特別適合于既有線的加固與強(qiáng)化[1]。前期既有研究工作主要針對(duì)附加應(yīng)力擴(kuò)散規(guī)律及其分布特征研究、預(yù)應(yīng)力路基邊坡穩(wěn)定性分析方法的構(gòu)建、合理板間距的初步設(shè)計(jì)思路、靜力性能數(shù)值仿真分析以及預(yù)應(yīng)力損失理論研究等方面[2-6]。而對(duì)于列車荷載與水平預(yù)應(yīng)力耦合作用下預(yù)應(yīng)力路基的動(dòng)力響應(yīng)規(guī)律還暫未研究。

眾所周知，現(xiàn)場(chǎng)測(cè)試、模型試驗(yàn)與數(shù)值仿真分析是研究鐵路路基動(dòng)力響應(yīng)特性的主要手段[7-9]。現(xiàn)場(chǎng)試驗(yàn)可以最真實(shí)地反映列車作用下路基的工作狀態(tài)，但因測(cè)試位置常限于路基外輪廓，故難以獲得路基內(nèi)部核心區(qū)域的響應(yīng)特性。模型試驗(yàn)則以小比尺為主，因其相似判據(jù)難以一一滿足，導(dǎo)致試驗(yàn)結(jié)果無(wú)法完全映射至實(shí)際工況。隨著計(jì)算機(jī)的快速發(fā)展，數(shù)值仿真方法以成本低、可操作性強(qiáng)、分析工況可控、數(shù)據(jù)提取全面、模型尺寸可調(diào)等優(yōu)點(diǎn)，成為解決各類工程問(wèn)題的高效研究手段，并在鐵路路基動(dòng)力響應(yīng)分析中得到了廣泛應(yīng)用。

近年來(lái)，已有大量鐵路路基動(dòng)力響應(yīng)方面的有限元模型被提出。如：CHEN等[10-11]建立了無(wú)砟軌道路基的三維有限元模型，分析表明路基動(dòng)應(yīng)力峰值隨列車運(yùn)行速度的增大而增大。莊妍等[12]建立了樁承式路堤三維有限元模型，發(fā)現(xiàn)線路豎向速度與加速度從道床頂面到地基頂面均衰減了80%。XU 等[13]基于車輛-軌道耦合動(dòng)力學(xué)理論[14]，建立了國(guó)內(nèi)重載鐵路典型路基段三維動(dòng)力有限元模型，指出列車相鄰轉(zhuǎn)向架引起的動(dòng)力響應(yīng)存在顯著的疊加效應(yīng)。商擁輝等[15]開展了列車-有砟軌道-基床-地基動(dòng)力系統(tǒng)耦合三維有限元仿真分析，發(fā)現(xiàn)重載鐵路列車運(yùn)行時(shí)，動(dòng)應(yīng)力影響深度達(dá)3～4 m，超過(guò)基床設(shè)計(jì)厚度2.5 m。此外，軌道不平順通過(guò)影響輪-軌接觸關(guān)系而影響路基的動(dòng)力響應(yīng)[16-17]。KOUROUSSIS等[18]研究了輪-軌不平順關(guān)系，并總結(jié)了輪-軌類型和輪-軌接觸狀態(tài)對(duì)振動(dòng)響應(yīng)的影響。

綜上可知，目前關(guān)于鐵路路基動(dòng)力響應(yīng)特性方面的研究已取得較為豐碩的研究成果，但其分析對(duì)象均為常規(guī)路基，而新型預(yù)應(yīng)力路基在常規(guī)路基中引入了預(yù)應(yīng)力加固結(jié)構(gòu)，是一種全新的路基結(jié)構(gòu)體系，其結(jié)構(gòu)形式必然異于既有研究對(duì)象，故現(xiàn)有關(guān)于鐵路路基動(dòng)力響應(yīng)方面的研究成果無(wú)法反映預(yù)應(yīng)力路基動(dòng)力響應(yīng)規(guī)律。因此，目前亟待開展鐵路預(yù)應(yīng)力路基在動(dòng)力性能方面的研究工作，合理探究列車動(dòng)載、軌道不平順以及水平預(yù)應(yīng)力耦合作用對(duì)路基動(dòng)力響應(yīng)特性的影響。本文作者建立列車-軌道-路基(預(yù)應(yīng)力路基和常規(guī)路基)三維動(dòng)力有限元數(shù)值模型，并考慮軌道不平順的影響，對(duì)比研究不同列車軸重下，常規(guī)路基與預(yù)應(yīng)力路基基床層內(nèi)動(dòng)應(yīng)力響應(yīng)規(guī)律以及預(yù)應(yīng)力路基中核心施力構(gòu)件(預(yù)應(yīng)力鋼筋)的振動(dòng)響應(yīng)特性，系統(tǒng)揭示預(yù)應(yīng)力路基結(jié)構(gòu)的瞬態(tài)動(dòng)力響應(yīng)特性。

1 列車-軌道-路基-預(yù)應(yīng)力加固結(jié)構(gòu)三維動(dòng)力有限元數(shù)值模型

1.1 重載列車模型

為反映前后節(jié)車廂相鄰轉(zhuǎn)向架的振動(dòng)疊加效應(yīng)，本文模型選取2節(jié)車廂。其中，車廂、轉(zhuǎn)向架和輪軸設(shè)置為剛體。懸掛連接系統(tǒng)采用Cartesian形式的線性彈簧-阻尼單元。建立如圖1 所示具有10個(gè)自由度的車輛模型。車體和轉(zhuǎn)向架考慮沉浮、點(diǎn)頭振動(dòng)位移，而輪對(duì)僅考慮沉浮振動(dòng)位移[19]。圖1中：Mc為車體質(zhì)量；Jc為車體點(diǎn)頭慣量；Mt為構(gòu)架質(zhì)量；Jt為構(gòu)架點(diǎn)頭慣量；Mw為輪對(duì)質(zhì)量；Kpz為一系懸掛剛度；Cpz為一系懸掛阻尼；Ksz為二系懸掛剛度；Csz為二系懸掛阻尼。

圖1 二系懸掛系統(tǒng)力學(xué)連接關(guān)系Fig. 1 Mechanical connection relation with double suspension system

本文為對(duì)比分析大軸重列車作用下常規(guī)路基和預(yù)應(yīng)力路基的瞬態(tài)動(dòng)力響應(yīng)差異，分別選取列車軸重25 t、30 t和35 t共3種工況，具體幾何參數(shù)如表1所示，其中35 t軸重列車采用C96敞車模擬，敞車結(jié)構(gòu)見(jiàn)圖2；車輛結(jié)構(gòu)計(jì)算參數(shù)如表2所示。

表1 重載列車幾何參數(shù)Table 1 Geometric parameters of heavy-haul train

表2 車輛結(jié)構(gòu)計(jì)算參數(shù)Table 2 Calculation parameters of vehicle structure

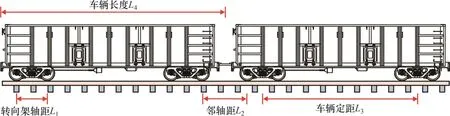
圖2 列車結(jié)構(gòu)參數(shù)Fig. 2 Geometrical specification of train

1.2 軌道-路基-預(yù)應(yīng)力加固結(jié)構(gòu)模型

常規(guī)軌道-路基系統(tǒng)主要結(jié)構(gòu)為鋼軌、墊板、扣件、軌枕、道砟、路基和地基；而預(yù)應(yīng)力路基則增添了預(yù)應(yīng)力加固結(jié)構(gòu)(即預(yù)應(yīng)力鋼筋和側(cè)壓力板)，如圖3 所示。數(shù)值模型中，鋼軌與軌枕間采用線性彈簧-阻尼連接器模擬二者間的傳力模式以替代扣件和墊板的作用，其豎向剛度取100 MN/m，豎向阻尼系數(shù)取6×104N·s/m，彈簧-阻尼單元的縱向間距為0.60 m，如圖4所示。側(cè)壓力板、軌枕及下部結(jié)構(gòu)層均采用C3D8R 單元類型，鋼筋選用二力桿T3D2單元。路基體3個(gè)結(jié)構(gòu)層(基床表層、基床底層和路基本體)和地基層均采用Mohr-Coulomb本構(gòu)模型，其余構(gòu)件如軌枕、預(yù)應(yīng)力鋼筋和側(cè)壓力板則考慮成線彈性體。本文重點(diǎn)分析2種路基結(jié)構(gòu)在不同軸重列車運(yùn)行下路基的動(dòng)應(yīng)力響應(yīng)規(guī)律，未考慮道砟顆粒如何準(zhǔn)確傳遞列車荷載作用，因此，道砟層也采用線彈性模型。軌枕-路基-地基耦合模型的本構(gòu)參數(shù)取值參照朔黃重載鐵路各結(jié)構(gòu)層的相關(guān)試驗(yàn)結(jié)果[20]，具體如表3所示。

表3 軌道-路基-預(yù)應(yīng)力構(gòu)件的材料參數(shù)Table 3 Material properties of track subgrade and prestressed members

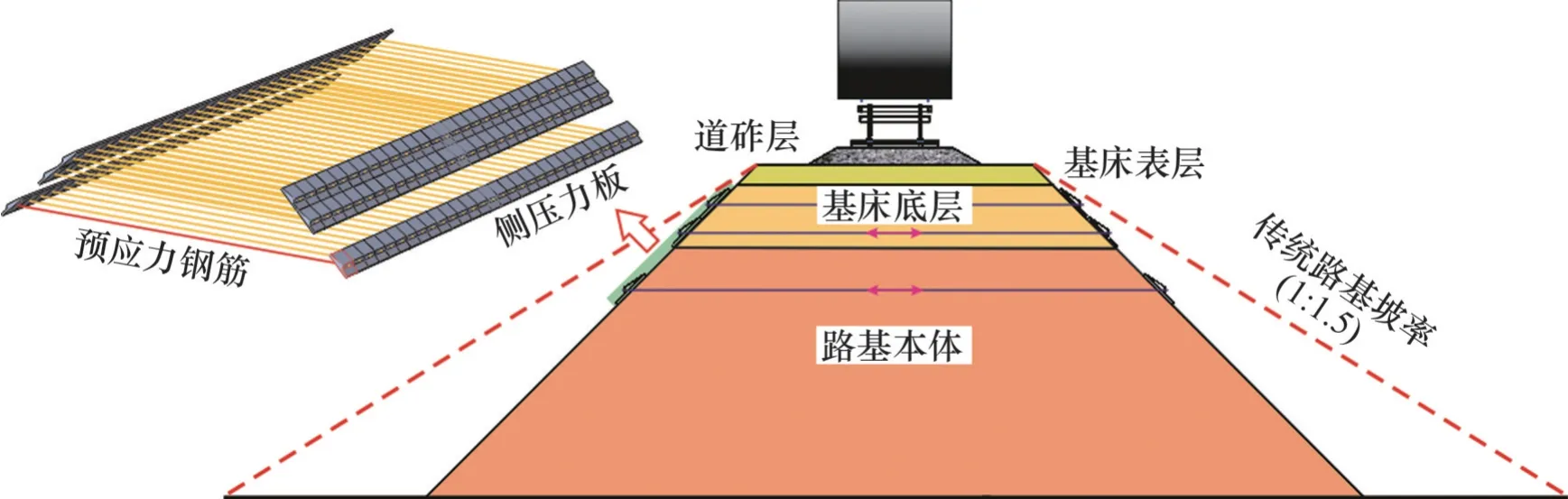
圖3 預(yù)應(yīng)力路基結(jié)構(gòu)示意圖Fig. 3 Schematic diagram of prestressed subgrade structure

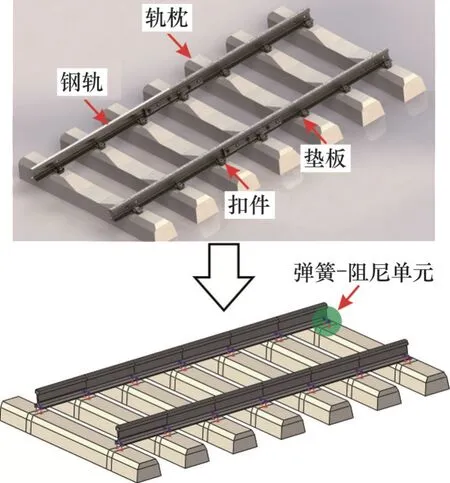
圖4 鋼軌-軌枕間的連接方式Fig. 4 Connection mode between rail and sleeper

為使預(yù)應(yīng)力鋼筋達(dá)到目標(biāo)張拉值，不因滿足變形協(xié)調(diào)而出現(xiàn)預(yù)拉力損失，本文采用Bolt Load法[21]模擬鋼筋預(yù)應(yīng)力的張拉和鎖定，如圖5 所示。此外，鋼筋端部與側(cè)壓力板間的連接采用耦合約束替代錨固元件作用，力學(xué)模式為平動(dòng)自由度(U1、U2、U3)受約束，而轉(zhuǎn)動(dòng)自由(UR1、UR2、UR3)，較貼合二者實(shí)際工作狀態(tài)。因側(cè)壓力板在正常工作中很難向上滑動(dòng)，即側(cè)壓力板與路基邊坡應(yīng)保持為緊密接觸狀態(tài)，因此，板-土接觸關(guān)系在法向設(shè)置為“硬接觸”，而切向設(shè)置為“粗糙接觸”，以確保側(cè)壓力板穩(wěn)定“趴”于路基坡面。

圖5 側(cè)壓力板與預(yù)應(yīng)力鋼筋Fig. 5 Lateral pressure plates and prestressed steel bars

軌道-路基結(jié)構(gòu)幾何尺寸依據(jù)重載鐵路設(shè)計(jì)規(guī)范中的標(biāo)準(zhǔn)單線斷面尺寸建立，具體幾何尺寸見(jiàn)表4。其中，側(cè)壓力板底面邊長(zhǎng)設(shè)為1.2 m，預(yù)應(yīng)力鋼筋直徑為25 mm，規(guī)格為HPB300熱軋光圓鋼筋，對(duì)應(yīng)公稱截面積為4.098×10-4m2。考慮到預(yù)應(yīng)力鋼筋對(duì)坡面?zhèn)葔毫Π宓膶?duì)拉約束作用，同時(shí)也為更好地體現(xiàn)預(yù)應(yīng)力結(jié)構(gòu)的加固作用，本文將常規(guī)路基坡率由1:1.5調(diào)整為1:1.0。

表4 軌道-路基模型幾何參數(shù)Table 4 Geometrical parameters of track subgrade model

1.3 輪-軌接觸模型

為避免模型網(wǎng)格入侵導(dǎo)致計(jì)算不收斂，需合理設(shè)置輪-軌接觸對(duì)中的主從面關(guān)系。在此，車輪設(shè)為剛體，鋼軌為彈性體，輪-軌接觸采用面-面接觸關(guān)系，車輪表面為主面，鋼軌表面為從面，具體關(guān)系如圖6所示。

求解列車與軌道間的動(dòng)力學(xué)運(yùn)動(dòng)方程需建立有效的輪-軌力學(xué)接觸關(guān)系。常用的輪-軌接觸關(guān)系采用非線性Hertz 接觸理論和罰函數(shù)摩擦(Penalty)模型，分別考慮法向和切向接觸行為，其計(jì)算精度高且易收斂。因此，本文切向接觸關(guān)系中的切向摩擦因數(shù)取0.2。在軌道平順條件下，法向相互作用由Hertz非線性彈性接觸理論確定[14]：

式中：P(t)表示某時(shí)刻t對(duì)應(yīng)的輪軌法向作用力；δz(t)表示某時(shí)刻t對(duì)應(yīng)的輪軌豎向相對(duì)壓縮值；G表示輪軌接觸常數(shù)。

輪軌接觸常數(shù)G在針對(duì)磨損型踏面車輪時(shí)，按式(2)計(jì)算取值。

式中：R表示車輪半徑。

對(duì)于不平順軌道情形，本文以單節(jié)車廂4個(gè)輪對(duì)為研究對(duì)象，則某時(shí)刻t對(duì)應(yīng)的輪軌法向接觸力Pj(t) (j=1，2，3，4)可按式(3)進(jìn)行計(jì)算。

式中：Zwj(t)、Zr(xwj，t)和Z0(t)分別表示某時(shí)間t對(duì)應(yīng)第j個(gè)輪對(duì)下的沉浮位移、鋼軌位移和軌面高低不平順位移。則據(jù)此可得單節(jié)車廂4個(gè)輪對(duì)組與鋼軌間的法向接觸力。

采用Soft-Contact中的Tabular模式來(lái)描述上述輪軌法向接觸行為，而定義該行為時(shí)需預(yù)設(shè)接觸面的過(guò)盈量與接觸力的關(guān)系，當(dāng)輪軌脫離產(chǎn)生間隙時(shí)，接觸壓力為0，如圖7所示。

圖7 輪-軌法向接觸模式示意圖Fig. 7 Schematic diagram of wheel-rail normal contact mode

1.4 軌道不平順

軌道不平順會(huì)對(duì)行車安全及平穩(wěn)舒適性構(gòu)成不利影響。依據(jù)激擾方位的不同，軌道不平順可分為高低不平順、水平不平順、軌距不平順和軌向不平順。其中，高低、水平不平順對(duì)系統(tǒng)的垂向激擾程度最大，而水平不平順是由高低不平順派生而來(lái)[22]。因此，本文僅考慮高低不平順。

徐磊等[23]基于朔黃重載鐵路的軌道不平順檢測(cè)數(shù)據(jù)，獲得了表征朔黃重載鐵路線路不平順特征的軌道譜函數(shù)。本文結(jié)合研究重點(diǎn)，采用其高低不平順的軌道譜建議表達(dá)式：

式中：S(f)為軌道不平順功率譜；f為空間頻率；a、b、c和d為譜密度函數(shù)的擬合特征參數(shù)，各參數(shù)具體數(shù)值如表5所示。

表5 朔黃重載鐵路軌道高低不平順統(tǒng)計(jì)譜特征參數(shù)Table 5 Characteristic parameters of vertical irregularity track spectrum of Shenchi—Huanghua heavy haul railway

軌道不平順常用的模擬方法為逆傅里葉變換法、三角級(jí)數(shù)法、二次濾波法和白噪聲濾波法。逆傅里葉變換可比較真實(shí)地再現(xiàn)線路的空間不平順狀態(tài)。故本文采用快速傅里葉逆變換(IFFT)方法將不平順軌道功率譜轉(zhuǎn)化為沿線路縱向的空間分布不平順?lè)怠?/p>

將上述朔黃重載鐵路軌道高低不平順功率譜利用Matlab 軟件轉(zhuǎn)化成沿線路縱向連續(xù)隨機(jī)分布的不平順?lè)担⑷】臻g波長(zhǎng)0.5～100.0 m，車輛運(yùn)行速度v=80 km/h，即可得到左、右高低不平順樣本幅值沿路基線路縱向的空間分布圖。軌道高低不平順建模過(guò)程如圖8所示。

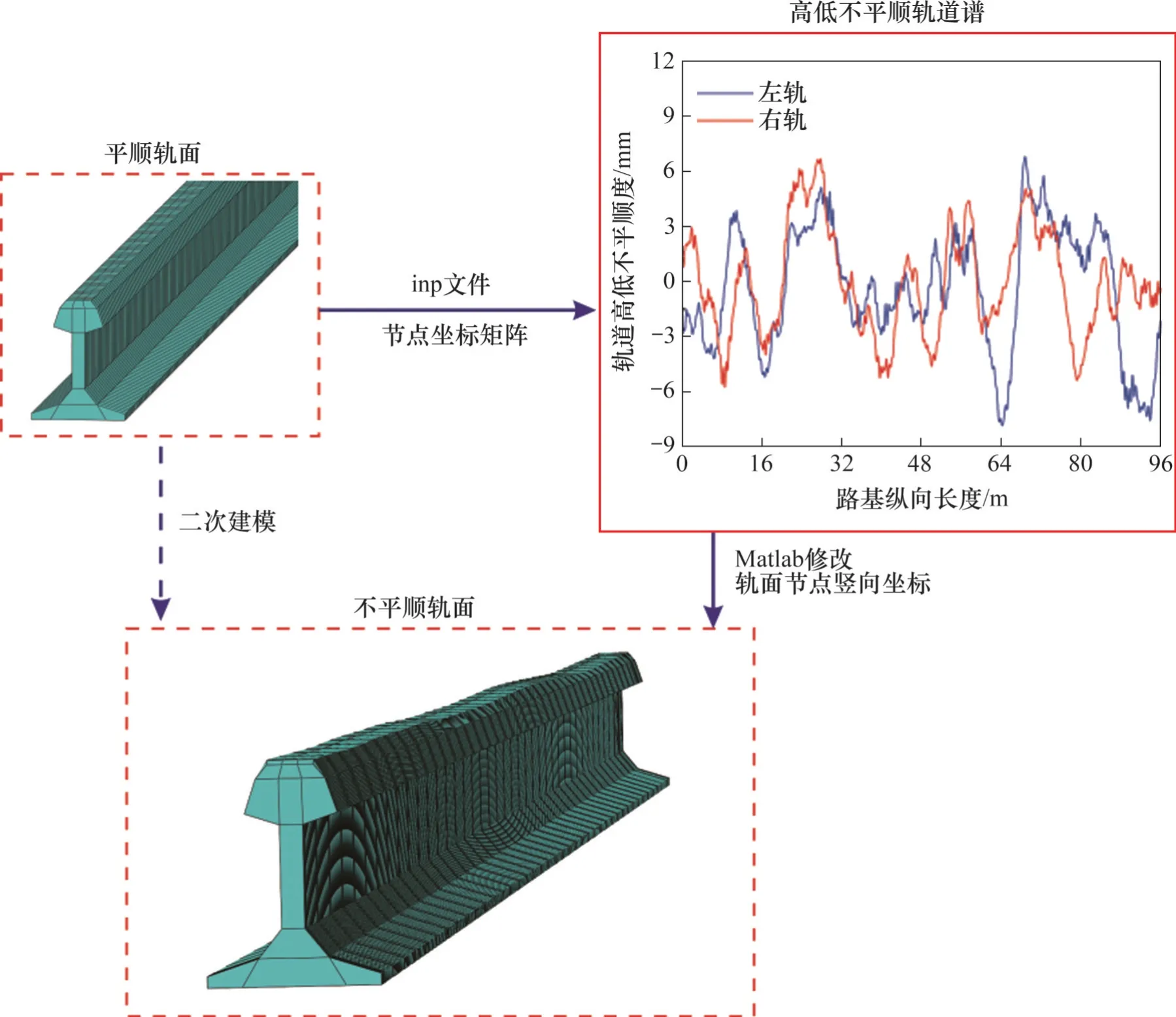
圖8 軌道高低不平順建模過(guò)程Fig. 8 Modeling process of track vertical irregularity

1.5 材料阻尼參數(shù)

阻尼決定振動(dòng)能量衰減的快慢，數(shù)值模型中除軌枕、側(cè)壓力板和預(yù)應(yīng)力鋼筋外，將道砟層、路基結(jié)構(gòu)層和地基均考慮為黏彈性體，采用Rayleigh阻尼模型，其阻尼矩陣C是由質(zhì)量矩陣M和剛度矩陣K線性組合而成[24]：

式中：αR為質(zhì)量比例阻尼系數(shù)；βR為剛度比例阻尼系數(shù)；D為阻尼比；ω1為模型基頻；ω2為對(duì)路基系統(tǒng)動(dòng)力響應(yīng)有顯著影響的高階振型頻率。

采用振型疊加法對(duì)路基模型進(jìn)行模態(tài)分析，以獲得路基結(jié)構(gòu)的振型和固有頻率[25]。計(jì)算確定該路基模型中的兩個(gè)目標(biāo)圓頻率分別為ω1=9.815 rad/s 和ω2=15.152 rad/s。本文模型中材料的阻尼比D取值見(jiàn)文獻(xiàn)[19]，將ω1、ω2和D分別代入式(6)和式(7)可獲得各結(jié)構(gòu)層的阻尼系數(shù)αR和βR。表6所示為各結(jié)構(gòu)層的Rayleigh阻尼參數(shù)。對(duì)于模型端部動(dòng)力邊界的處理，由于距離列車動(dòng)荷載較遠(yuǎn)，可采用黏彈性人工高阻尼吸能邊界，將阻尼比D設(shè)置為1.0，以模擬無(wú)限遠(yuǎn)地基吸收動(dòng)力波并減少邊界反射波的影響[19]。

表6 模型材料Rayleigh阻尼計(jì)算參數(shù)Table 6 Model material Rayleigh damping calculation parameters

路基在列車荷載作用下的應(yīng)力分量中豎向應(yīng)力分量最大，且基床層動(dòng)力響應(yīng)程度最高[25]。因此，本文重點(diǎn)分析兩種路基結(jié)構(gòu)鋼軌正下方處的豎向動(dòng)應(yīng)力峰值，以此對(duì)比二者在動(dòng)力瞬態(tài)響應(yīng)方面的差異。

1.6 路基模型與分析過(guò)程

分別建立常規(guī)路基和預(yù)應(yīng)力路基三維動(dòng)力有限元模型，如圖9所示。圖中，X軸代表線路橫斷面方向，Y軸代表豎直方向，Z軸代表線路縱向。由于有限元模型尺寸對(duì)計(jì)算量和計(jì)算精度均有一定影響，故考慮兩個(gè)路基模型的縱向長(zhǎng)為96 m，橫向(X向)邊界距路基坡腳32.25 m。路基模型深度的設(shè)置需結(jié)合路基動(dòng)力響應(yīng)的衰減情況考慮，重載鐵路路基面以下2.5 m深度處動(dòng)應(yīng)力衰減量可達(dá)60%[13]，則文中模型中地基深度設(shè)為10 m，模型底部距路基面的距離達(dá)到18 m，滿足計(jì)算精度要求。常規(guī)路基模型節(jié)點(diǎn)數(shù)為685 699個(gè)，單元數(shù)為567 078 個(gè)，網(wǎng)格最大尺寸為11.7 m，最小尺寸為0.013 m；預(yù)應(yīng)力路基模型節(jié)點(diǎn)數(shù)為719 413個(gè)，單元數(shù)為590 514 個(gè)，網(wǎng)格最大尺寸為11.7 m，最小尺寸為0.013 m。

圖9 車輛-軌道-路基(預(yù)應(yīng)力路基)三維有限元模型Fig. 9 3D finite element model of train-track-subgrade(prestressed subgrade) system

基床層受列車動(dòng)荷載影響最為顯著，而其圍壓水平很低，屬于病害重點(diǎn)源區(qū)。預(yù)應(yīng)力路基具體加固方案為從基床底層底面向上連續(xù)布置兩排預(yù)應(yīng)力加固結(jié)構(gòu)(第1、2排)，另外在路基本體段布置第3排加固結(jié)構(gòu)，為提高預(yù)應(yīng)力在路基內(nèi)的擴(kuò)散均勻性，采用1.0倍板寬作為第2、3排加固結(jié)構(gòu)間的上下凈間距(見(jiàn)圖10)。冷伍明等[5,26]的研究表明，當(dāng)側(cè)壓力板布置在距離坡面路肩小于2.0倍板寬的凈距離時(shí)，極易引起路肩段土體發(fā)生“上拱剪切破壞”，故第1 排鋼筋預(yù)拉力初始值為其余各排的50%，即第1～3排加固結(jié)構(gòu)的等效預(yù)壓面荷載分別為50、100、100 kPa。在該種加固模式下，依據(jù)預(yù)應(yīng)力路基附加圍壓擴(kuò)散理論[5]，可計(jì)算出雙側(cè)預(yù)應(yīng)力加固結(jié)構(gòu)在基床表層對(duì)應(yīng)鋼軌正下方位置所產(chǎn)生的附加圍壓約為30 kPa，由此提高基床層圍壓水平與側(cè)限作用。

圖10 預(yù)應(yīng)力加固結(jié)構(gòu)布置方案Fig. 10 Layout scheme of prestressed reinforced structure

在預(yù)應(yīng)力路基中，每橫排沿線路縱向連續(xù)布置30 塊側(cè)壓力板。針對(duì)2 種路基結(jié)構(gòu)中間段(36 m長(zhǎng)度范圍)內(nèi)的動(dòng)力響應(yīng)開展對(duì)比分析。模型邊界條件設(shè)置為：地基底面采用全固定約束，路基縱向兩端采用法向?qū)ΨQ約束，模型橫向兩端約束X向位移。表7所示為本文的具體仿真工況。

表7 仿真計(jì)算工況Table 7 Numerical simulation cases

對(duì)2種路基結(jié)構(gòu)開展動(dòng)力仿真分析時(shí)，首先都采用Geostatic 分布步模擬產(chǎn)生初始自重應(yīng)力場(chǎng)，即施加地基、路基和軌道部分的自重荷載，它可自動(dòng)清除位移場(chǎng)。對(duì)于后續(xù)分析步，常規(guī)路基僅添加列車移動(dòng)荷載作用即可；而對(duì)于預(yù)應(yīng)力路基，在完成自重應(yīng)力場(chǎng)分析后，計(jì)算預(yù)應(yīng)力加固結(jié)構(gòu)的自重作用，再?gòu)埨摻钪聊繕?biāo)預(yù)應(yīng)力，由此形成預(yù)應(yīng)力路基，最后計(jì)算移動(dòng)列車荷載。

2 模型驗(yàn)證

表8所示為文獻(xiàn)中有關(guān)現(xiàn)場(chǎng)試驗(yàn)[27-30]、模型試驗(yàn)[31]及數(shù)值模擬[13,15,32]的結(jié)果與本文常規(guī)路基數(shù)值模擬結(jié)果的對(duì)比。由表8可知：本文模型動(dòng)應(yīng)力峰值結(jié)果與既有文獻(xiàn)結(jié)果位于同一數(shù)量級(jí)且峰值較為接近，在數(shù)值上具有較高的可信度，基本驗(yàn)證了本文數(shù)值模擬結(jié)果的正確性。

表8 重載鐵路路基面動(dòng)應(yīng)力峰值統(tǒng)計(jì)Table 8 Peak value statistics of dynamic stress on subgrade surface of heavy-haul railway

3 基床層動(dòng)應(yīng)力峰值統(tǒng)計(jì)分析與正態(tài)性檢驗(yàn)

3.1 路基面動(dòng)應(yīng)力時(shí)程特征分析

未經(jīng)特別指出，文中動(dòng)應(yīng)力均指豎直方向的動(dòng)應(yīng)力。以線路縱向橫斷面Z=48 m(沿線路縱向中間截面)為研究對(duì)象，提取兩種路基結(jié)構(gòu)在不同軸重列車運(yùn)行條件下，左、右鋼軌正下方路基面P1和P2(見(jiàn)圖11)的動(dòng)應(yīng)力時(shí)程曲線，如圖12 所示。由圖12 可知：兩種路基結(jié)構(gòu)下的路基面動(dòng)應(yīng)力受列車軸重影響顯著，軸重越大，動(dòng)應(yīng)力水平越高，且左、右軌高低不平順使鋼軌下路基面動(dòng)應(yīng)力也產(chǎn)生了差異。同時(shí)，當(dāng)前后節(jié)車廂兩個(gè)相鄰轉(zhuǎn)向架通過(guò)時(shí)，其動(dòng)應(yīng)力水平相對(duì)較高，易達(dá)到峰值水平，這是兩個(gè)相鄰轉(zhuǎn)向架4個(gè)輪對(duì)共同作用產(chǎn)生的動(dòng)力疊加效果。

圖11 路基動(dòng)應(yīng)力峰值分析位置Fig. 11 Analysis position of dynamic stress peak value of subgrade

對(duì)于斷面Z=48 m處，在列車軸重為25、30和35 t作用下，常規(guī)路基左軌下方路基面動(dòng)應(yīng)力峰值分別為67.10、85.21和94.27 kPa，右軌下方路基面動(dòng)應(yīng)力峰值分別為67.32、85.38和97.98 kPa；而預(yù)應(yīng)力路基左軌下方路基面動(dòng)應(yīng)力峰值在3 種軸重列車作用下分別為66.18、84.11和92.99 kPa，右軌下方路基面動(dòng)應(yīng)力峰值分別為65.73、83.47 和95.75 kPa。雖然兩種路基結(jié)構(gòu)間的動(dòng)應(yīng)力峰值差異較小，但在同一斷面處，預(yù)應(yīng)力路基動(dòng)應(yīng)力峰值普遍略低于常規(guī)路基動(dòng)應(yīng)力峰值，且在35 t軸重列車作用下，動(dòng)應(yīng)力峰值間的最大差值為2.23 kPa。

圖13所示為兩種路基結(jié)構(gòu)在不同運(yùn)行時(shí)間下，路基面動(dòng)應(yīng)力等值線分布云圖(軸重30 t)。由圖13可知：左、右軌高低不平順?lè)笛鼐€路縱向存在相對(duì)高差，這導(dǎo)致路基面動(dòng)應(yīng)力在沿線路中線出現(xiàn)非對(duì)稱分布特征，且差異化明顯。在同一轉(zhuǎn)向架所控制的2個(gè)輪載作用下，路基面動(dòng)應(yīng)力云圖大致呈矩形分布，而2節(jié)車廂對(duì)應(yīng)4個(gè)轉(zhuǎn)向架在不同時(shí)刻下，路基面上的動(dòng)應(yīng)力分布表現(xiàn)為動(dòng)態(tài)隨機(jī)響應(yīng)，即每個(gè)矩形內(nèi)動(dòng)應(yīng)力的分布形態(tài)各不相同，且每個(gè)矩形內(nèi)的最大值也存在差別，這與列車運(yùn)行過(guò)程中受軌面不平順?biāo)鸬拇瓜螯c(diǎn)頭、沉浮運(yùn)動(dòng)密切相關(guān)，使得路基面動(dòng)應(yīng)力峰值的隨機(jī)分布特點(diǎn)顯著。此外，根據(jù)應(yīng)力等值圖例可知，2種路基結(jié)構(gòu)在相同時(shí)刻下，路基面動(dòng)應(yīng)力峰值差異不太顯著。具體來(lái)說(shuō)，在t=1.0 s 時(shí)，預(yù)應(yīng)力路基動(dòng)應(yīng)力峰值略大于常規(guī)路基動(dòng)應(yīng)力峰值；而在t=2.0 s 時(shí)，則是常規(guī)路基動(dòng)應(yīng)力峰值略高于預(yù)應(yīng)力路基動(dòng)應(yīng)力峰值。

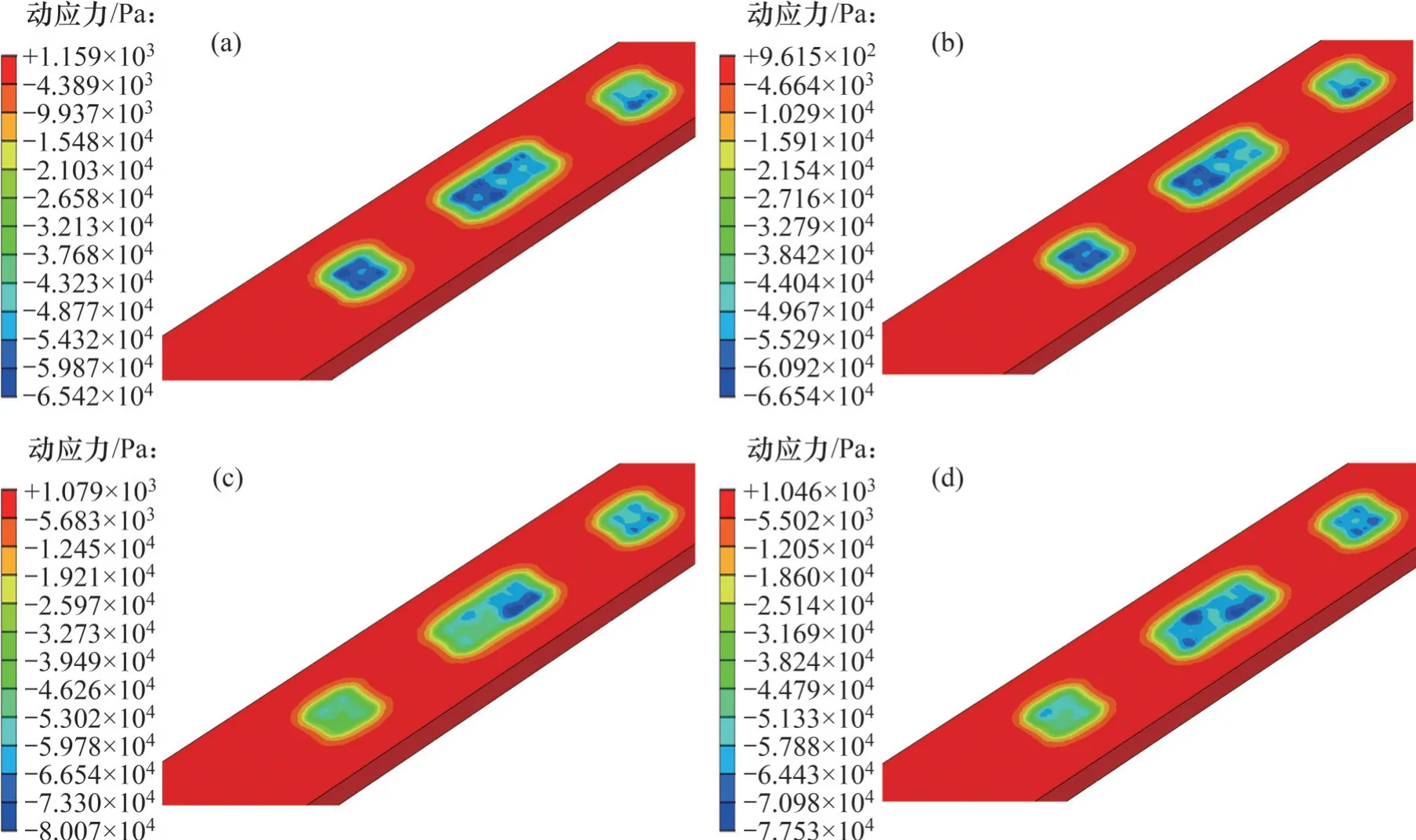
圖13 兩種路基結(jié)構(gòu)在不同時(shí)刻路基面動(dòng)應(yīng)力云圖(軸重為30 t)Fig. 13 Dynamic stress contours of subgrade surface of two subgrade structures at different times (axle load of 30 t)

沿線路縱向逐個(gè)提取軌下路基面網(wǎng)格單元的動(dòng)應(yīng)力峰值，經(jīng)數(shù)據(jù)整理可獲得其分布曲線，如圖14所示。由圖14可知：受軌道高低不平順的影響，軌下路基面動(dòng)應(yīng)力峰值沿線路縱向在一定范圍內(nèi)呈波動(dòng)分布，具有一定隨機(jī)性。

圖14 路基面動(dòng)應(yīng)力峰值沿線路縱向分布曲線Fig. 14 Distributions curves of peak dynamic stresses on subgrade surface along track

由圖14可知：2種路基結(jié)構(gòu)下的動(dòng)應(yīng)力峰值隨機(jī)離散分布程度均隨列車軸重的增大而增大；在同一軸重下，預(yù)應(yīng)力路基動(dòng)應(yīng)力峰值的整體離散程度相對(duì)偏低。以左軌下方路基面為例，當(dāng)列車軸重為35 t 時(shí)，常規(guī)路基動(dòng)應(yīng)力峰值變動(dòng)區(qū)間為[71.4，119.3] kPa，而預(yù)應(yīng)力路基動(dòng)應(yīng)力峰值變化范圍為[73.3，111.0] kPa；當(dāng)列車軸重為30 t時(shí)，常規(guī)路基動(dòng)應(yīng)力峰值波動(dòng)區(qū)間為[60.7，103.3] kPa，預(yù)應(yīng)力路基變化范圍為[61.7，97.7] kPa；當(dāng)列車軸重為25 t時(shí)，常規(guī)路基和預(yù)應(yīng)力路基下的動(dòng)應(yīng)力峰值變動(dòng)區(qū)間分別為[49.4，91.2] kPa 和[49.5，88.5] kPa。綜上可知，預(yù)應(yīng)力加固結(jié)構(gòu)在控制路基面動(dòng)應(yīng)力離散程度方面具有一定的積極作用，且軸重越大，控制優(yōu)勢(shì)越明顯。

3.2 基床層內(nèi)不同深度動(dòng)應(yīng)力峰值統(tǒng)計(jì)分析

在基床層左、右軌正下方沿垂向提取5個(gè)深度處的動(dòng)應(yīng)力峰值進(jìn)行分析(見(jiàn)圖11)，分別對(duì)應(yīng)路基面以下深度z為0、0.50、1.12、1.76 和2.40 m。圖15所示為2種路基結(jié)構(gòu)在不同列車軸重作用下，鋼軌下方基床層不同深度處的動(dòng)應(yīng)力峰值統(tǒng)計(jì)均值。從圖5 可以看出：由于預(yù)應(yīng)力加固結(jié)構(gòu)的強(qiáng)化作用，預(yù)應(yīng)力路基的動(dòng)應(yīng)力峰值統(tǒng)計(jì)均值在不同深度均略低于常規(guī)路基的動(dòng)應(yīng)力峰值，而2種路基結(jié)構(gòu)在3種不同軸重的列車作用下，基床層內(nèi)動(dòng)應(yīng)力峰值均值沿深度衰減規(guī)律基本一致，近似呈負(fù)指數(shù)衰減。可采用動(dòng)應(yīng)力衰減系數(shù)η來(lái)描述動(dòng)應(yīng)力峰值在2種路基結(jié)構(gòu)基床層內(nèi)的衰減規(guī)律。通過(guò)對(duì)動(dòng)應(yīng)力峰值均值與深度進(jìn)行負(fù)指數(shù)公式擬合，可獲得二者間的具體關(guān)系表達(dá)式，如圖16 所示，決定系數(shù)R2=0.99。可見(jiàn)預(yù)應(yīng)力路基基床層內(nèi)動(dòng)應(yīng)力衰減速率略低于常規(guī)路基動(dòng)應(yīng)力衰減速率。同時(shí)，本文數(shù)值仿真計(jì)算獲得的路基動(dòng)應(yīng)力平均水平隨基床深度的衰減曲線與文獻(xiàn)[31]中室內(nèi)足尺模型試驗(yàn)的實(shí)測(cè)曲線較為接近，由此也進(jìn)一步論證了三維動(dòng)力有限元仿真模型的可靠性。

圖15 基床層動(dòng)應(yīng)力峰值統(tǒng)計(jì)均值Fig. 15 Statistical mean value of dynamic stress peak value in subgrade bed layer

圖16 動(dòng)應(yīng)力衰減系數(shù)沿基床層深度變化的關(guān)系曲線Fig. 16 Relation curves of dynamic stress attenuation coefficient along the depth in subgrade bed layer

由于軌道沿線路縱向存在高低不平順，使路基動(dòng)應(yīng)力沿線分布呈顯著的隨機(jī)波動(dòng)性。對(duì)此，采用概率統(tǒng)計(jì)學(xué)中的“變異系數(shù)”對(duì)2種路基結(jié)構(gòu)動(dòng)應(yīng)力峰值數(shù)據(jù)的離散性進(jìn)行對(duì)比分析。圖17 所示為左、右軌下動(dòng)應(yīng)力峰值變異系數(shù)隨基床層深度變化的統(tǒng)計(jì)結(jié)果。由圖17可知：列車軸重越大，動(dòng)應(yīng)力峰值變異水平越高，即動(dòng)應(yīng)力波動(dòng)離散程度越大，表明列車軸重對(duì)路基動(dòng)應(yīng)力存在變異放大效應(yīng)，這進(jìn)一步提升了對(duì)線路基礎(chǔ)在抗動(dòng)載方面的性能要求。此外，基床層動(dòng)應(yīng)力變異系數(shù)同樣隨深度逐漸衰減，且衰減速率由快及緩，與動(dòng)應(yīng)力均值隨深度變化規(guī)律類似。由于預(yù)應(yīng)力結(jié)構(gòu)的強(qiáng)化作用，基床內(nèi)的動(dòng)應(yīng)力峰值變異性得到了改善，且列車軸重越大，越能體現(xiàn)出預(yù)應(yīng)力加固結(jié)構(gòu)在控制路基動(dòng)應(yīng)力離散程度方面的優(yōu)勢(shì)。在列車軸重為35 t時(shí)，常規(guī)路基右軌下方基床內(nèi)的動(dòng)應(yīng)力峰值變異系數(shù)范圍為5.33%～14.12%，而預(yù)應(yīng)力路基內(nèi)的變異系數(shù)范圍為4.95%～12.5%。因此，可認(rèn)為預(yù)應(yīng)力加固結(jié)構(gòu)對(duì)維持路基動(dòng)應(yīng)力穩(wěn)定存在有利作用，可在一定程度上抑制軌道高低不平順給路基體帶來(lái)的動(dòng)力放大效應(yīng)。

圖17 動(dòng)應(yīng)力變異系數(shù)沿基床層深度變化的統(tǒng)計(jì)規(guī)律Fig. 17 Statistical law of variation coefficient of dynamic stress along the depth in subgrade bed layer

3.3 基床層動(dòng)應(yīng)力峰值正態(tài)性檢驗(yàn)

文獻(xiàn)[33]指出，輪對(duì)荷載的分布形式較符合正態(tài)分布，而輪載可通過(guò)扣件由鋼軌傳遞至軌道結(jié)構(gòu)最終擴(kuò)散至路基內(nèi)。對(duì)此，可采用柯?tīng)柲缏宸?斯米洛夫(K-S)檢驗(yàn)法對(duì)軌下基床層內(nèi)的動(dòng)應(yīng)力峰值開展正態(tài)性檢驗(yàn)，具體過(guò)程如下。

1) 若有限元仿真計(jì)算所得的動(dòng)應(yīng)力峰值樣本(X1，X2，…，Xn)假定來(lái)自于總體樣本X，則可求出其較優(yōu)估計(jì)的經(jīng)驗(yàn)分布函數(shù)Fn(σ)，而Fn(σ)為理論分布函數(shù)，假設(shè)基床層內(nèi)動(dòng)應(yīng)力峰值均符合正態(tài)分布形式，據(jù)此可提出2個(gè)相對(duì)立的假設(shè)，即

H0：動(dòng)應(yīng)力峰值樣本來(lái)自的總體服從正態(tài)分布，F(xiàn)n(x)=F0(x)；

H1：動(dòng)應(yīng)力峰值樣本來(lái)自的總體不服從正態(tài)分布，F(xiàn)n(x)≠F0(x)。

2) 取K-S檢驗(yàn)統(tǒng)計(jì)量：

式(8)表示樣本所服從的總體分布與理論分布間的最大差值。顯然，當(dāng)2個(gè)分布比較接近時(shí)，Dn就較小，可認(rèn)為假設(shè)H0成立；反之，認(rèn)為該假設(shè)不成立。具體可采用一個(gè)顯著性水平α下對(duì)應(yīng)的臨界值Dn,α進(jìn)行判別，當(dāng)Dn

3) 求取待驗(yàn)證分布列的經(jīng)驗(yàn)累積分布函數(shù)Fn(σi)為

4) 判斷沿線路縱向分布的動(dòng)應(yīng)力峰值是否服從以下理論正態(tài)分布：

式中：為動(dòng)應(yīng)力樣本均值；S*為標(biāo)準(zhǔn)差。

根據(jù)上述檢驗(yàn)方法可計(jì)算出Dn，本文選取顯著性水平α=0.01，查K-S 檢驗(yàn)的臨界值表[34]可知Dn,α=1.63/(n)0.5，經(jīng)計(jì)算Dn,α=0.121 5。

表9所示為3種列車軸重作用下，左、右軌下方基床內(nèi)5個(gè)不同深度處的Dn。由表9可知：每個(gè)深度位置處的統(tǒng)計(jì)值Dn均小于臨界值Dn,α，表明受軌道不平順的影響，基床內(nèi)動(dòng)應(yīng)力峰值沿線路縱向均服從正態(tài)分布規(guī)律。圖18 所示為30 t 軸重列車作用下，2種路基結(jié)構(gòu)在左軌下方路基面的動(dòng)應(yīng)力峰值沿線路縱向的統(tǒng)計(jì)結(jié)果及其正態(tài)分布預(yù)測(cè)曲線。可見(jiàn)常規(guī)路基的動(dòng)應(yīng)力分布域更大，數(shù)據(jù)相對(duì)離散。

表9 基床層動(dòng)應(yīng)力峰值正態(tài)分布檢驗(yàn)統(tǒng)計(jì)表Table 9 Statistical table of normality test of peak dynamic stresses in subgrade bed layer

圖18 左軌下方路基面動(dòng)應(yīng)力頻數(shù)直方圖與預(yù)測(cè)分布曲線對(duì)比(軸重為30 t)Fig. 18 Comparison between frequency histogram of dynamic stress on subgrade surface under left rail and predicted distribution curve (axle load of 30 t)

4 預(yù)應(yīng)力鋼筋附加動(dòng)應(yīng)力峰值統(tǒng)計(jì)分析

作為預(yù)應(yīng)力結(jié)構(gòu)中的核心施力構(gòu)件，預(yù)應(yīng)力鋼筋在列車動(dòng)荷載作用下的內(nèi)力變化情況可在一定程度上反映出加固結(jié)構(gòu)的整體振動(dòng)響應(yīng)特性。對(duì)此，著重分析鋼筋附加應(yīng)力的變化情況。

圖19 所示為30 t 軸重列車作用下，各橫排第15 根預(yù)應(yīng)力鋼筋(S1、S2 和S3)的附加動(dòng)應(yīng)力時(shí)程曲線。由圖19 可知：S1 動(dòng)應(yīng)力響應(yīng)程度最高，當(dāng)轉(zhuǎn)向架通過(guò)時(shí)，其動(dòng)應(yīng)力時(shí)程曲線振蕩響應(yīng)相對(duì)最大，表明此時(shí)鋼筋處于受力劇烈變化階段，且在前后節(jié)車廂相鄰轉(zhuǎn)向架通過(guò)時(shí)同樣出現(xiàn)了附加動(dòng)應(yīng)力峰值；而S2和S3的附加動(dòng)應(yīng)力響應(yīng)程度沿坡面向下逐漸衰減。預(yù)應(yīng)力鋼筋S1至S3的動(dòng)應(yīng)力時(shí)程曲線形態(tài)由“三峰式”逐漸過(guò)渡為“單峰式”，這是由于路基體存在一定的阻尼耗能作用，使得坡面振動(dòng)響應(yīng)從路肩往坡腳逐漸衰減弱化。鋼筋附加動(dòng)應(yīng)力響應(yīng)水平由大到小順序?yàn)镾1、S2、S3。

圖19 預(yù)應(yīng)力鋼筋附加動(dòng)應(yīng)力時(shí)程曲線(軸重為30 t)Fig. 19 Additional dynamic stress time history curves of prestressed steel bars (axle load of 30 t)

沿線路縱向提取路基內(nèi)各橫排預(yù)應(yīng)力鋼筋的附加動(dòng)應(yīng)力峰值，其分布曲線如圖20 所示。從圖20 可以看出：列車軸重越大，鋼筋附加動(dòng)應(yīng)力峰值水平越高。每橫排端部預(yù)應(yīng)力鋼筋的附加動(dòng)應(yīng)力峰值較大，這是由于加固結(jié)構(gòu)端部處于常規(guī)路基段與預(yù)應(yīng)力路基段的交界過(guò)渡區(qū)，該位置加固效果在整個(gè)預(yù)應(yīng)力路基段內(nèi)最弱，當(dāng)列車經(jīng)過(guò)此端部過(guò)渡區(qū)時(shí)，列車動(dòng)載對(duì)該突變區(qū)產(chǎn)生相對(duì)較大的沖擊效應(yīng)，增大了鋼筋動(dòng)應(yīng)力響應(yīng)水平。此外，第1排預(yù)應(yīng)力鋼筋在不同軸重列車作用下所引起的附加動(dòng)應(yīng)力差異明顯，且各分布曲線沿線路縱向波動(dòng)幅度相對(duì)較大，第2排鋼筋在不同軸重的列車作用下對(duì)應(yīng)的分布曲線間差異水平有所下降，而第3排鋼筋間的分布曲線差異性最小，且曲線變化相對(duì)平穩(wěn)，這表明動(dòng)荷載經(jīng)基床層快速衰減后，到達(dá)路基本體上的坡面振動(dòng)響應(yīng)已較低且處于相對(duì)穩(wěn)定狀態(tài)。

圖20 預(yù)應(yīng)力鋼筋附加動(dòng)應(yīng)力峰值沿線路縱向分布曲線Fig. 20 Longitudinal distribution curves of additional dynamic stress peak of prestressed steel bars along track

表10 所示為同軸重的列車作用下，各排鋼筋附加動(dòng)應(yīng)力峰值沿線路縱向分布的平均值。由表10可知：由于第1排預(yù)應(yīng)力加固結(jié)構(gòu)布置在基床層中部坡面，其動(dòng)應(yīng)力峰值水平相對(duì)最高，但與鋼筋靜態(tài)目標(biāo)張拉應(yīng)力相比，其振動(dòng)響應(yīng)程度很低。如在35 t軸重列車作用下，第1排鋼筋附加動(dòng)應(yīng)力均值僅為7.136 MPa，而目標(biāo)張拉應(yīng)力為146.7 MPa，其變化率低于5%，表明預(yù)應(yīng)力鋼筋在列車荷載經(jīng)過(guò)時(shí)，所受振動(dòng)影響程度很低，響應(yīng)偏于緩和。此外，盡管第1、2 排加固結(jié)構(gòu)是沿基床底層坡面緊密布置，但其間的附加動(dòng)應(yīng)力均值存在較大差別，表明振動(dòng)作用在基床層衰減較快；而第3排加固結(jié)構(gòu)因布置在路基本體，鋼筋振動(dòng)響應(yīng)水平最低，其均值水平僅為第1 排鋼筋的26.4%，可見(jiàn)其附加動(dòng)應(yīng)力已大幅衰減，表明在路基本體段布置的預(yù)應(yīng)力加固結(jié)構(gòu)受列車動(dòng)載影響甚微。

表10 預(yù)應(yīng)力鋼筋附加動(dòng)應(yīng)力峰值統(tǒng)計(jì)均值Table 10 Statistical mean value of additional dynamic stress peak of prestressed steel bars

5 結(jié)論

1) 列車軸重越大，基床層動(dòng)應(yīng)力水平越高。受軌道不平順的影響，左、右鋼軌下路基面動(dòng)應(yīng)力峰值沿線路縱向分布存在顯著差異。

2) 路基面動(dòng)應(yīng)力沿線路縱向的隨機(jī)離散程度隨列車軸重增大而增大，且預(yù)應(yīng)力加固結(jié)構(gòu)可在一定程度上控制動(dòng)應(yīng)力峰值沿線路縱向的離散程度，且軸重越大，控制優(yōu)勢(shì)越顯著。

3) 采用變異系數(shù)和均值對(duì)兩種路基結(jié)構(gòu)基床層內(nèi)不同深度處的動(dòng)應(yīng)力峰值數(shù)據(jù)進(jìn)行統(tǒng)計(jì)分析，發(fā)現(xiàn)變異系數(shù)和平均值沿深度均是逐漸衰減的。在預(yù)應(yīng)力加固結(jié)構(gòu)作用下，預(yù)應(yīng)力路基基床內(nèi)動(dòng)應(yīng)力峰值的變異性得到改善，且列車軸重越大，改善效果相對(duì)越顯著。

4) 基于柯?tīng)柲缏宸?斯米洛夫(K-S)檢驗(yàn)法，驗(yàn)證了兩種路基在軌下基床層內(nèi)不同深度的動(dòng)應(yīng)力峰值沿線路縱向均具有正態(tài)性。

5) 預(yù)應(yīng)力鋼筋振動(dòng)響應(yīng)程度沿坡面向下逐漸衰減，其時(shí)程曲線表現(xiàn)為由“三峰式”過(guò)渡為“單峰式”。而鋼筋附加動(dòng)應(yīng)力遠(yuǎn)小于目標(biāo)張拉應(yīng)力，表明預(yù)應(yīng)力鋼筋受上部列車動(dòng)載的振動(dòng)影響程度低。