轉折角對 Z 形通道印刷電路板式換熱器中二氧化碳流動與換熱特性的影響

沈佳飛　王波　周秋平　王雅亮　成金東

摘要：針對超臨界二氧化碳氣冷堆核電系統中 Z 形通道印刷電路板式換熱器的優化設計，通過數值模擬研究轉折角對印刷電路板式換熱器中二氧化碳流動和換熱特性的影響規律，分別擬合出摩擦因子和努塞爾數的計算關聯式，分析傳熱過程的熱阻，并討論換熱器的綜合性能。結果表明，摩擦因子和對流換熱系數均隨轉折角的增大呈拋物線規律增長，在轉折角小于 20 °時增長較慢。導熱熱阻占總傳熱熱阻的 4.16%～16.02%，并隨二氧化碳質量流率和轉折角的增大而升高，在印刷電路板式換熱器的傳熱計算中，不應被忽略。隨著轉折角的增加，通道中努塞爾數的增長幅度小于摩擦因子的增長幅度，傳遞相同熱量的泵送功率增大，但所需換熱面積減小，換熱器的制造成本下降，實際應用中需進一步通過技術經濟分析以選取最佳轉折角。為了控制通道中流動阻力占進口壓力的比例，轉折角以不超過 20 °為宜。

關鍵詞：印刷電路板式換熱器；轉折角；二氧化碳；流動阻力；傳熱

中圖分類號：? TK 172???????????? 文獻標志碼：?? A

Effect of turning angle on flow and heat transfer characteristics of carbon dioxide in zigzag printed circuit heat exchangers

SHENJiafei1，WANG Bo1，ZHOU Qiuping2，WANGYaliang1，CHENG Jindong1

（1. School of Energy and Power Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China;2. Zhejiang Dun'an Machinery and Electronics Technology Co.， Ltd.， Shaoxing 311800， China）

Abstract： Toachievetheoptimaldesignofzigzagprintedcircuitheatexchanger （PCHE） inthe supercritical carbon dioxide gas-cooled reactor nuclear power system， the influence of the turning angle on the flow and heat transfer characteristics of carbon dioxide in PCHEs was studied by numerical simulation，andthecorrelationsforFanningfrictionfactorandNusseltnumbercalculationwere obtained. The thermal resistance of the heat transfer process was analyzed， and the comprehensive performance of the heat exchanger was discussed. The results show that the Fanning friction factor and convective heat transfer coefficient both increase parabolically with the increase of the turning angle， and the growth is relatively slow when the turning angle is less than 20°. The thermal conductionresistance accounts for 4.16% ～? 16.02%? of the overall thermal resistance， and it increases with the increase of the mass flow rate and the turning angle. It should not be ignored in the heat transfer calculation of printed circuit heat exchanger. With the increase of the turning angle， the increase of the Nusselt number is smaller than that of the Fanning friction factor. The pumping power for transferring the same heat increases， but the required heat exchange area decreases. The manufacturing cost are reduced， and in practical applications， further techno-economic analysis is required to select the optimal turning angle. To control the proportion of the flow resistance in the channel to the inlet pressure， the turning angle should not exceed 20° .

Keywords： printed circuit heat exchanger ; turning? angle ; carbon? dioxide; flow? resistance; heat transfer

印刷電路板式換熱器（ printedcircuitheatexchanger ，PCHE）是一種高效緊湊式換熱器，工作溫度范圍廣，承壓能力可達60 MPa，在相同換熱條件下比傳統管殼式換熱器的體積減小約85%，有利于降低傳熱過程的溫差和不可逆損失，可用于太陽能熱發電、核電和船舶液化天然氣供應等系統中[1-3]。PCHE 芯體由多層蝕刻有流體通道的金屬板片經擴散焊接制成，通道型式是影響 PCHE 性能的關鍵因素，有直通道、Z 形通道、 S 形翅片通道和翼型翅片通道等結構。 Chai 等[4]通過數值模擬研究了半圓形截面直通道 PCHE 內超臨界二氧化碳（supercritical carbon dioxide ， S-CO2）的流動和換熱特性，發現局部對流放熱系數從入口處開始沿流動方向迅速下降，然后保持穩定，存在明顯的入口效應。李磊等[5]比較了不同通道 PCHE 中氦氣的流動特性，發現半圓形截面 Z 形通道 PCHE 的阻力系數大于直通道。 Chu 等[6]對 Z 形通道 PCHE 中 S-CO2和水的換熱進行了實驗研究，獲得了努塞爾數和摩擦系數的計算關聯式。謝瑤等[7]研究了 PCHE 中液化天然氣的傳熱系數與流動阻力隨質量流率、熱通量和溫度的變化規律。 Cheng 等[8]研究了 Z 形通道 PCHE 預冷器中 S- CO2和水的換熱，分析了工質流量和進口溫度對流動阻力、換熱系數、溫度效率的影響。 Wen 等[9] 研究了波形通道 PCHE 中，波形通道的波幅和波長對 S-CO2流動和傳熱性能的影響，結果表明，相對較小的波幅有利于提高綜合性能。宋丹等[10] 對超臨界液化天然氣在錯列 S 形通道 PCHE 中的對流換熱過程進行了數值模擬，分析了擬臨界工況附近的對流換熱特征。 Ma 等[11]研究了翅片橫向節距、縱向節距和有無端壁圓角對翼型翅片通道 PCHE 熱工水力性能的影響。針對典型應用場景，氦氣[12-14]、超臨界甲烷[15-16]、超臨界二氧化碳[17-19]和熔鹽[20-21]等工質在 PCHE 中的流動和換熱特性研究受到廣泛關注。

在采用 S-CO2冷卻反應堆并直接通過 S-CO2布雷頓循環發電的新一代氣冷堆核電系統方案中，普遍采用 PCHE作為回熱器，其優化設計有利于提高循環效率。在不同通道結構的 PCHE 中， Z 形通道 PCHE制造難度和成本較低，傳熱性能和應用前景較好[22]。通道轉折角是 Z 形通道 PCHE 的重要結構參數，對 PCHE 性能的影響尚需進一步研究。因此，本文針對 S-CO2氣冷堆核電系統中低溫回熱器的傳熱問題，通過數值模擬分析不同轉折角 Z 形通道 PCHE 中二氧化碳的流動和換熱特性，為回熱器的優化設計和性能實驗提供參考。

1 物理模型和數值方法

1.1 物理模型

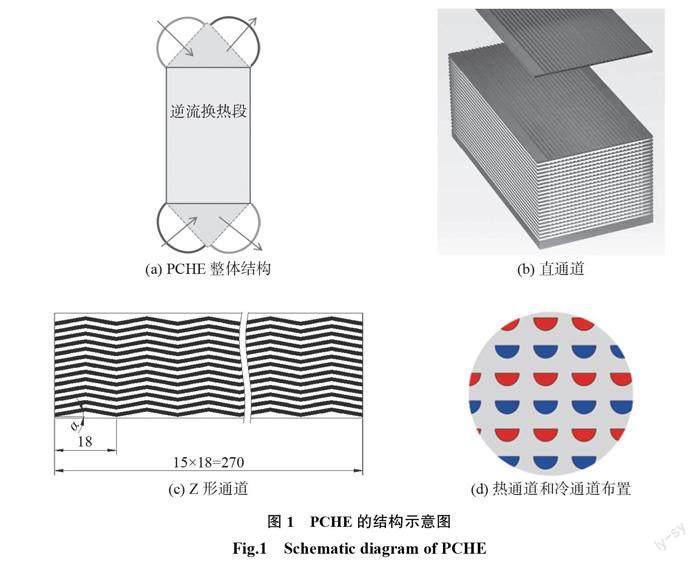
圖1（a）為逆流換熱 PCHE 整體結構示意圖，逆流換熱段芯體的直通道結構如圖1（b）所示，Z 形通道結構如圖1（c）所示。冷流體和熱流體通道均為半圓形截面，上下分層交替布置，如圖1（d）所示。通道截面半徑1.0 mm，水平方向節距3.2 mm，高度方向節距2.2 mm；每個 Z 形通道沿流動方向節距為18 mm ，共15個節距，總節距270 mm。 Z 形通道轉折角分別為0（直通道），5，10，15，20，30，45°。換熱器材料為316L不銹鋼，導熱系數為16.2 W/（m?K）。

1.2 網格模型

鑒于 Z 形通道 PCHE 通道布置的周期性特征，并假定熱流體和冷流體在各自流動通道中的流量分配均勻，選取圖2所示雙層通道換熱單元為數值模擬對象，熱通道在上，冷通道在下，不同參數的二氧化碳逆向流過上下通道進行換熱，固體域截面寬3.2 mm 、高4.4 mm、總節距270 mm。圖2（b）為其中1個節距范圍內的三維結構。采用 ICEM 軟件對固體域和流體域進行結構化網格的劃分，半圓形截面通道采用 O 形網格，流體通道壁面附近進行網格加密。

在數值模擬過程中，對網格進行無關性驗證。圖3為通道轉折角=30° ， 冷通道和熱通道中二氧化碳質量流率 G=200 kg/（m2·s），采用不同網格尺寸時，冷通道中流體壓降和對流換熱系數的計算結果。當網格數達到6191874以后，壓降和對流換熱系數的計算結果變化十分緩慢，網格數進一步增加到10751736，計算結果相對偏差僅為0.16%和0.51%。因此，該工況下的模擬應選取網格數量為6191874的網格模型。

1.3 邊界條件

PCHE 固體域上下壁面和左右壁面設置為周期性邊界條件，進口端和出口端壁面設置為絕熱邊界條件，流體通道的壁面為流固耦合界面。流體域入口采用質量流量入口，出口采用壓力出口。熱側二氧化碳入口溫度和壓力分別為553.15 K 和3.2 MPa，冷側二氧化碳入口溫度和壓力分別為381.15 K 和10.5 MPa。冷側和熱側的入口質量流率相等，質量流率的范圍為100～400 kg/（m2?s）。

1.4 物性參數

二氧化碳的熱物理性質隨壓力和溫度變化。由于 PCHE 進口二氧化碳的壓力高，進出口壓差和進口壓力的比值較小，故近似認為熱通道和冷通道中二氧化碳的物性參數僅隨溫度變化。通過 REFPROP 軟件分別查取10.5 MPa 和3.2 MPa 壓力下，350～600 K 范圍內二氧化碳的密度ρ、動力黏度μ、定壓比熱容 cp 和導熱系數λ， 并擬合為關于溫度 T 的函數，結果如表1所示，擬合優度 R2均高于0.97。

1.5 計算模型與求解方法

在本文研究的工況范圍內，二氧化碳在 Z 形通道中流動的雷諾數均大于2000，湍流模型采用 k-ε模型，近壁區采用標準壁面函數。采用 SIMPLE 算法實現速度與壓力的耦合求解，變量梯度采用 Least Squares Cell Based 方法求解，壓力方程采用標準離散格式，動量方程和能量方程的離散采用二階迎風格式，湍流方程的離散采用一階迎風格式，所有變量收斂精度為10?6。該數值模擬方法已廣泛用于 PCHE 中二氧化碳傳熱特性研究，數值模擬與實驗結果吻合較好[14，23]。Wang等[24]也對本文的模型進行了驗證，分析表明，計算模型比較合理。

1.6 數據處理

流體通道的水力直徑

式中： V 表示流體通道的體積；A 表示流體通道的壁面積。

范寧摩擦因子

式中：ΔPf表示流體的壓降；表示流體平均密度； L 表示流體通道的長度； u表示通道有效截面上的平均速度。

流體和通道壁面間的平均表面對流換熱系數

式中： q 表示平均熱流密度；ΔTm表示壁面和流體的平均溫差。

流體和通道壁面間對流換熱的努塞爾數

式中：λ表示流體的平均導熱系數。

本文研究的 PCHE 中，熱通道和冷通道結構完全相同，大端溫差ΔTd和小端溫差ΔTx 的比值小于2，ΔTm可近似采用算術平均溫差，即

式中： Tw 表示平均壁溫；Tf表示流體平均溫度。

以任一側流體通道壁面積為基準，熱流體和冷流體通過金屬壁傳熱的總傳熱系數

式中：Tf，h為熱流體平均溫度；Tf，c為冷流體平均溫度。

在數值模擬中不考慮污垢熱阻，故導熱熱阻

式中：hh， hc分別為熱通道與冷通道的平均表面對流換熱系數。

Z 形通道 PCHE 采用不同通道轉折角，會影響流體和通道壁面間的平均表面換熱系數，以及流體的流動阻力，所以，采用綜合評價因子ζ評價Z 形通道強化換熱的綜合性能

ζ=ΔP（ΔPfr） f = Nf（u）/（/）fref（Nur）ef（8）

式中：下標 ref 表示參比通道，本文選取轉折角為0°的直通道為參比通道。

在相同的流體進口質量流率和溫度下，ζ可以反映傳遞相同熱量時不同轉折角 PCHE 中流體流動阻力的高低[25]。

2 結果與分析

2.1PCHE 中二氧化碳的流動特性

2.1.1 PCHE 中二氧化碳的壓力分布

為了探討轉折角對二氧化碳流動和換熱特性的影響，對直通道 PCHE 和轉折角為5，10，15，20，30，45°的每一種 Z 形通道 PCHE，分別模擬二氧化碳質量流率為100，150，200，250，300，350，400 kg/（m2?s）的7個工況。模擬結果表明，在所有49個工況中，基于每個通道內二氧化碳平均熱物性計算所得流動雷諾數最低為5031，最高為20370，均處于湍流狀態。

熱通道和冷通道中二氧化碳的壓力沿流動方向都近似線性變化。以轉折角30°、質量流率250 kg/（m2·s）的工況為例，冷通道和熱通道中二氧化碳的壓力分布分別如圖4（a）和（b）所示。從圖中可以看出，冷通道中二氧化碳的壓力從10.5 MPa 線性下降到10.4874 MPa，流動阻力12.6 kPa，流動阻力和進口壓力的比值為1.2‰；熱通道中二氧化碳的壓力從3.2 MPa線性下降到3.1546 MPa，流動阻力45.4 kPa，流動阻力和進口壓力的比值為14.2‰。

2.1.2轉折角對二氧化碳流動壓降的影響

通道中二氧化碳的壓降隨質量流率和轉折角的增大而增大。如圖5所示，在400 kg/（m2·s）的質量流率下，對轉折角為0，5，10，15，20、30，45°的 PCHE，冷通道二氧化碳的壓降分別為6.881，7.035，7.811，9.947，13.796，29.592，86.581 kPa，與冷通道二氧化碳進口壓力的比值分別為0.66‰，0.67‰，0.74‰，0.95‰，1.31‰，2.82‰，8.25‰；熱通道二氧化碳的壓降分別為23.889，24.483，27.234，34.952，50.552，107.179，316.088 kPa ，與熱通道二氧化碳進口壓力的比值分別為7.46‰，7.65‰，8.51‰，10.92‰，15.80‰，33.49‰，98.78‰；熱通道二氧化碳的壓降是冷通道的3.47～3.65倍。由此可見，冷通道和熱通道結構相同、質量流率相等的條件下，冷通道二氧化碳進口壓力高，流動阻力小，而熱通道二氧化碳進口壓力低，流動阻力大，在 PCHE 設計中可增大熱通道流通面積以控制流動阻力。

2.1.3轉折角對流動通道摩擦因子的影響

二氧化碳在 PCHE 通道中流動的摩擦因子隨轉折角和質量流率變化的規律如圖6所示。在每個模擬工況中，熱通道和冷通道的轉折角和質量流率相同，摩擦因子也接近，而熱通道中二氧化碳的流動阻力高，主要是由熱通道中二氧化碳的壓力低、比容大引起的。對一定轉折角的 Z 形通道，由于流動進入紊流光滑管區，摩擦因子與雷諾數負相關，質量流率越大，雷諾數越大，摩擦因子越小。在相同的質量流率下，Z 形通道轉折角越大，摩擦因子越高，這是因為隨著轉折角的增大，流體通過轉折角處時方向變化更急，流動截面上速度不均勻性更大，流動分離加劇，流體對前方壁面的碰撞增強，再加上分離區存在二次流，導致能量耗散，增加局部阻力[26]。從圖 6 中還可以看出，摩擦因子隨轉折角呈拋物線規律變化。在一定的質量流率下，直通道的摩擦因子最小；當 Z 形通道轉折角小于 20?°時，摩擦因子隨轉折角的增大而緩慢增大；當轉折角大于 20?°時，隨著轉折角的增大，摩擦因子大幅增長。以質量流率400 kg/（m2·s）的工況為例，直通道 PCHE熱通道中二氧化碳平均密度34.79 kg/m3，摩擦因子為0.01176，流動阻力為23.889 kPa；轉折角20°的 Z 形通道 PCHE 熱通道中二氧化碳平均密度34.99 kg/m3，摩擦因子增大到0.02351，流動阻力增大到 50.552 kPa ；當轉折角為45°時，熱通道中二氧化碳平均密度35.32 kg/m3，摩擦因子達到0.11165，流動阻力高達316.088 kPa。流動阻力增加的幅度顯著超過摩擦因子增加的幅度，這是因為在相同的總節距下，流動通道總長度和轉折角的余割值成正比，轉折角越大，不僅摩擦因子增加，流動通道也越長；轉折角為45°時，在相同的總節距下，其流動通道長度是直通道的1.414倍。在不同轉折角下，熱通道內二氧化碳的平均密度略有變化，是影響熱通道流動阻力的次要因素。因此，將轉折角控制在20°以下，有利于避免過大的流動阻力。

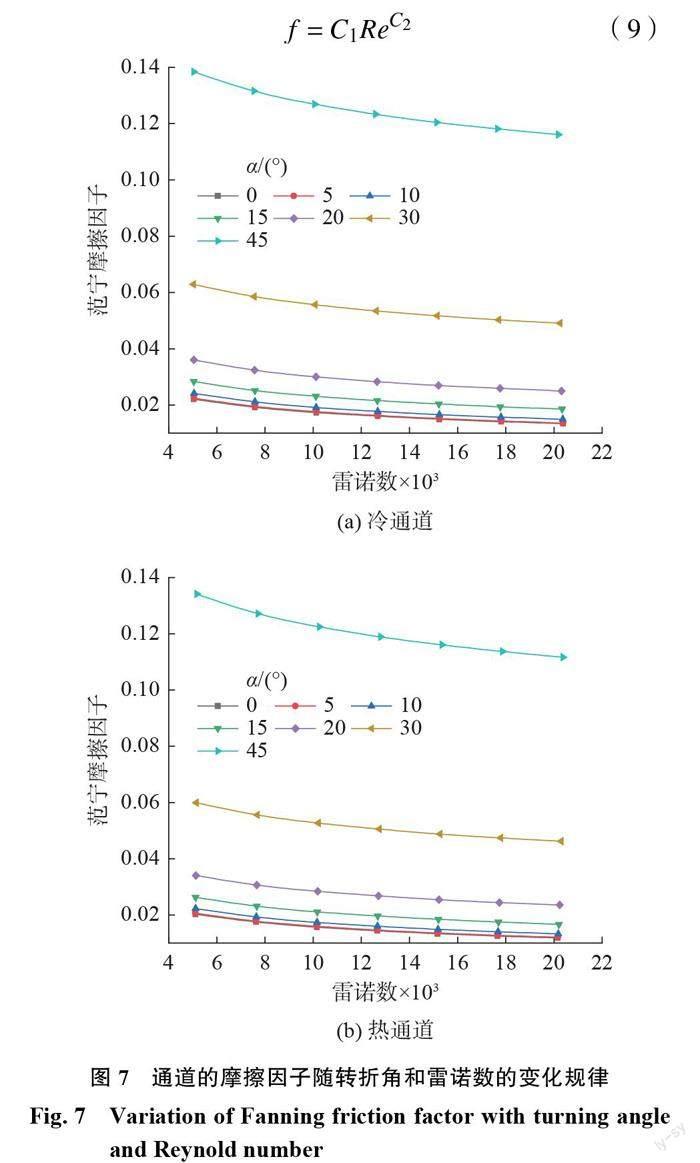
通道內二氧化碳流動的摩擦因子與雷諾數的關系如圖7所示。在本文研究的每一個工況下，冷通道和熱通道中二氧化碳的質量流率相同，盡管冷通道中二氧化碳壓力高、溫度低，熱通道中二氧化碳壓力低、溫度高，兩側流體的動力黏度卻很接近，相對偏差都在3%以內，因而兩側流動的雷諾數也非常接近。在相同的雷諾數下，冷通道中二氧化碳流動的摩擦因子比熱通道高約3%～14%；轉折角越大，兩側的摩擦因子相差越小。這可能是因為冷通道中二氧化碳溫度沿流動方向不是線性變化，進口端二氧化碳的溫度上升較快，出口端溫度上升較緩，按平均溫度查取密度后計算得到的平均速度和動壓略微偏小，使摩擦因子偏大一點。

2.1.4流動通道摩擦因子與雷諾數的關聯式

對摩擦因子和雷諾數進行非線性擬合

f = C1ReC2（9）

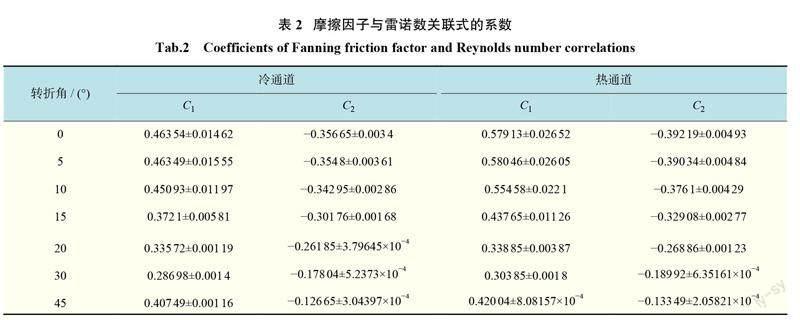
得到不同轉折角 Z 形通道 PCHE 中冷通道和熱通道摩擦因子與雷諾數之間關聯式的系數 C1和 C2，如表2所示。

2.2PCHE 中二氧化碳的換熱特性

2.2.1 PCHE 中二氧化碳的溫度分布

各工況下熱通道中二氧化碳的溫度沿流動方向近似線性下降，冷通道中二氧化碳在入口端沿流動方向溫度上升較快，然后平穩增長；冷通道入口端的傳熱溫差較大，往出口端逐漸減小，并在較大范圍內保持基本穩定。以轉折角30°、質量流率250 kg/（m2·s）條件下 Z 形通道 PCHE 內的流動為例，如圖8所示，冷通道中二氧化碳溫度從 381.15 K 上升到532.35K，熱通道中二氧化碳溫度從553.15 K 下降到430.41K，高溫端傳熱溫差20.8 K，低溫端傳熱溫差49.26 K。由于冷側進口二氧化碳比定壓熱容為1.490 kJ/（kg?K），熱側出口二氧化碳比定壓熱容為1.035 kJ/（kg?K），兩側質量流率相等，熱側和冷側交換一定的熱量后，引起的熱側二氧化碳溫降，應高于冷側二氧化碳的溫升，而圖中溫度分布表明低溫端冷側二氧化碳溫度反而上升快，傳熱溫差大，這意味著在 PCHE 中由于流動通道的水力直徑很小，冷熱通道之間的金屬壁從高溫端向低溫端的軸向導熱作用不可忽略。結果表明，在回熱器設計中如要進一步減小傳熱溫差，還需增加通道長度。

2.2.2轉折角對二氧化碳和通道壁面間對流換熱的影響

二氧化碳與 PCHE通道壁面間的對流換熱系數隨通道轉折角和質量流率的增大而增大。從圖9中可以看出，對流換熱系數隨轉折角呈拋物線規律增大，在一定的質量流率下，直通道的對流換熱系數最小；當 Z 形通道轉折角小于20°時，對流換熱系數隨轉折角的增大而緩慢增大；當轉折角大于20°時，隨著轉折角的增大，對流換熱系數的增幅加大。以質量流率400 kg/（m2·s）的工況為例，直通道 PCHE熱通道中二氧化碳和通道壁面間對流換熱系數為3268.4 W/（m2·K），轉折角20°的 Z 形通道 PCHE熱通道中二氧化碳和通道壁面間對流換熱系數增大到4004.6 W/（m2·K），轉折角45°的 Z 形通道 PCHE熱通道中二氧化碳和通道壁面間對流換熱系數進一步提高到6724.8 W/（m2·K）。這是由于轉折角增大時，流體經過轉折角處的流向改變更大，流動分離加劇，對前方壁面的沖刷增強，通過流體擾動更充分地破壞邊界層，從而增強與壁面的對流換熱。結合圖6可知，轉折角增大到45°， 對流換熱系數增長幅度遠遠低于摩擦因子增長的幅度，這會引起泵送功率的提高。

從圖10中可以看出，努塞爾數隨通道轉折角和雷諾數的增大而增大。在每個工況中，冷通道和熱通道的轉折角相等，結構完全相同，但是，在相同的雷諾數下，熱通道中努塞爾數比冷通道高出40%～150%，而且雷諾數越小，轉折角越大，熱通道中努塞爾數比冷通道中努塞爾數增加的幅度越大。

對努塞爾數和雷諾數、普朗特數進行非線性擬合：

Nu = C1ReC2Pr n（10）

式中：Pr為普朗特數； n 為系數，對熱通道， n 取0.3，對冷通道， n 取0.4。

不同轉折角 Z 形通道 PCHE 中冷通道和熱通道中努塞爾數關聯式的系數，如表3所示。

2.2.3轉折角對導熱熱阻的影響

本文研究的 PCHE 中上下2個相鄰的半圓形截面冷熱通道之間的壁厚是漸變的，可采用等效壁厚法計算冷熱通道之間的導熱熱阻[1，27]。等效壁厚

tw = t -（11）

式中： t 為冷熱通道之間的最大壁厚，對本文研究的 PCHE，其值為0.0022 m；r 為半圓形截面的半徑。

導熱熱阻

rw =（12）

式中：λw 為金屬的導熱系數。

采用等效壁厚法計算得到冷熱通道之間金屬壁的導熱熱阻為8.7321×10?5 m2·K/W。

通過數值模擬獲得的總傳熱系數隨轉折角和質量流率的變化規律如圖11所示。

根據總傳熱系數、熱通道的平均表面對流換熱系數和冷通道的平均表面對流換熱系數，按照式（7）計算可得傳熱過程的導熱熱阻。同一轉折角下，導熱熱阻隨質量流率的變化很小，近似為一個定值。對于轉折角0，5，10，15，20，30，45°的Z 形通道 PCHE，計算所得導熱熱阻分別為7.8522×10?5，7.8283×10?5，7.7639×10?5，7.7213×10?5，7.7565×10?5，7.8764×10?5，7.9214×10?5 m2·K/W，與采用等效壁厚法計算所得導熱熱阻的相對偏差分別為10.08%，10.35%，11.09%，11.58%，11.17%，9.80%，9.28%。等效壁厚法計算所得導熱熱阻偏高，其原因可能是等效熱阻法是簡化計算方法，沒有考慮轉折角對導熱的影響，也沒有考慮冷熱通道之間的金屬壁從高溫端向低溫端的軸向導熱作用。

在相同質量流率下，冷通道中二氧化碳的對流換熱熱阻在總傳熱熱阻中所占比重較大。以質量流率為100 kg/（m2·s）的工況為例，轉折角為0，5，10，15，20，30，45°時，冷通道對流換熱熱阻分別占總傳熱熱阻的60.04%，60.07%，60.23%，60.88%，61.53%，63.17%，65.31%。隨著質量流率的增大，冷通道熱阻在總熱阻中所占比重略有減小。如圖12所示，質量流率和轉折角越大，冷通道和熱通道的對流換熱熱阻越小，導熱熱阻占總傳熱熱阻的比例就越高。在所有的工況中，導熱熱阻占總傳熱熱阻的比例在4.16%～16.02%之間，表明在 PCHE 的傳熱計算中，不宜忽略導熱熱阻。2.3 轉折角對 PCHE 綜合性能的影響

通過上述分析可知，隨著 Z 形通道轉折角的增大， PCHE 換熱性能增強，同時流動阻力也會增大。為了綜合評價轉折角對 Z 形通道 PCHE 性能的影響，以直通道 PCHE 作為參比結構，按式（8）計算綜合評價因子ζ。

圖13為不同轉折角 PCHE 的綜合評價因子隨質量流率的變化規律。從圖中可以看出，所有轉折角下 PCHE 的綜合評價因子均小于1，表明摩擦因子的增長幅度大于努塞爾數的增長幅度。在相同的冷熱流體質量流率和進出口溫度下，與直通道 PCHE 相比，采用 Z 形通道 PCHE 時實現相同傳熱量，克服流動阻力所消耗的功率隨著轉折角的增大而升高，導致運行成本增加。但是，隨著轉折角的增大，努塞爾數提高，所需換熱面積減小，換熱器結構更緊湊，重量更輕，這將減小換熱器的制造成本。在 PCHE 設計時，需綜合考慮制造成本和運行成本，以及對發電循環效率的影響。結合圖5所示冷通道和熱通道流動阻力占冷通道進口壓力的比例，轉折角以不超過20°為宜，否則過大的流動阻力會降低布雷頓發電循環的效率。

3 結論

針對 S-CO2氣冷堆核電系統中低溫回熱器的傳熱，通過數值模擬分析不同轉折角 Z 形通道 PCHE 中二氧化碳的流動和換熱特性，得出如下結論：

a.冷通道和熱通道內二氧化碳流動和換熱過程中，摩擦因子和對流換熱系數均隨轉折角的增大呈拋物線規律變化，當 Z 形通道轉折角小于20°時，摩擦因子和對流換熱系數隨轉折角的增大而緩慢增大；當轉折角大于20°時，隨著轉折角的增大，摩擦因子和對流換熱系數增長幅度加大，且對流換熱系數增長幅度顯著低于摩擦因子增長幅度。

b.在 PCHE冷通道和熱通道結構相同、質量流率相等的條件下，熱通道中二氧化碳的流動阻力和對流換熱系數顯著高于冷通道，可考慮通過增加熱側二氧化碳流通截面積，降低熱通道中二氧化碳流速和阻力。

c.質量流率和轉折角越大，導熱熱阻占總傳熱熱阻的比例越高。在本文研究的工況中，導熱熱阻占總傳熱熱阻的比例在4.16%～16.02%之間，在 PCHE 的傳熱計算中，不宜忽略導熱熱阻。采用等效壁厚法計算所得的導熱熱阻相對偏大。

d.不同轉折角下 PCHE 的綜合評價因子均小于1，意味著在相同的質量流率和進出口溫度下，隨著轉折角的增加，傳遞相同熱量的泵送功率增大，但所需換熱面積減小，換熱器體積、重量和制造成本下降，在實際應用中應通過技術經濟分析以選取最佳轉折角。結合通道中流動阻力占進口壓力的比例，轉折角以不超過20°為宜，以免流動阻力過大導致布雷頓發電循環效率下降。

參考文獻：

[1]徐哲， 張明輝， 段天應， 等.超臨界二氧化碳在印刷電路板式換熱器內的流動換熱特性研究[J].原子能科學技術， 2021， 55（5）：849–855.

[2] KLEMES? J J. Compact heat exchangers for energy transfer intensification： low grade heat and fouling mitigation[M]. Boca Raton： CRC Press， 2016：101–104.

[3] NIKITINK，KATOY，NGOL. Printedcircuitheat exchanger thermal-hydraulic performanceinsupercritical CO2experimentalloop[J].InternationalJournalofRefrigeration， 2006， 29（5）：807–814.

[4] CHAIL，TASSOUSA. Numericalstudyofthe thermohydraulicperformanceofprintedcircuitheat exchangersforsupercriticalCO2Braytoncycle applications[J]. Energy Procedia， 2019， 161：480–488.

[5]李磊， 楊劍， 馬挺，等.印刷電路板通道的高溫傳熱和阻力特性研究[J].工程熱物理學報， 2014， 35（5）：931–934.

[6] CHU W X， LI X H， CHEN Y T， et al. Experimental study on small scale printed circuit heat exchanger with zigzag channels[J]. HeatTransferEngineering， 2021， 42（9）：723–735.

[7]謝瑤， 李劍銳， 胡海濤.印刷電路板式換熱器內超臨界甲烷流動換熱特性模擬[J].化工學報 ， 2021， 72（S1）：203–209.

[8] CHENGKY，ZHOUJZ，ZHANGHZ，etal. Experimentalinvestigationofthermal-hydraulic characteristics of a printed circuit heat exchanger used as a pre-coolerforthesupercriticalCO2Braytoncycle[J]. Applied Thermal Engineering， 2020， 171：115116.

[9] WEN Z X， LV Y G， LI Q， et al. Numerical study on heat transfer behavior of wavy channel supercritical CO2 printed circuitheatexchangerswithdifferentamplitudeand wavelengthparameters[J]. InternationalJournalofHeat and Mass Transfer， 2020， 147：118922.

[10]宋丹， 蔣慶峰， 馮國增， 等.超臨界 LNG 在錯列 S 形翅片微通道的流動傳熱特性研究[J].低溫與超導 ， 2021，49（1）：16–21.

[11] MA T， XIN F， LI L， et al. Effect offin-endwall fillet on thermal hydraulic performance of airfoil printed circuit heat exchanger[J]. AppliedThermalEngineering， 2015， 89：1087–1095.

[12] MCCORMACK D. The application of printed circuit heat exchanger technology in the pebble bed modular reactor demonstration plant[C]//Proceedings of ASME Turbo Expo 2001： Power for Land， Sea， and Air. New Orleans： ASME， 2001：2001-GT-0473.

[13] KIMIH，NOHC. Physicalmodeldevelopmentand optimal design of PCHE for intermediate heat exchangers in HTGRs[J]. Nuclear Engineering and Design， 2012， 243：243–250.

[14] KIMDE，KIMMH，CHAJE，etal. Numerical investigationonthermal –hydraulicperformanceofnew printedcircuitheatexchangermodel[J].Nuclear Engineering and Design， 2008， 238（12）：3269–3276.

[15]李瑋哲， 林文勝.超臨界甲烷在印刷電路板換熱器中加熱過程模擬[J].低溫工程， 2017（5）：60–64，74.

[16]賈丹丹， 趙忠超， 張永， 等.超臨界 LNG 在印刷板式汽化器微細流道內的流動與換熱性能數值研究[J].船舶工程， 2017， 39（5）：35–40.

[17] BAEKS，KIMJH，JEONGS，etal. Developmentof highlyeffectivecryogenic printedcircuitheatexchanger （PCHE） with low axial conduction[J]. Cryogenics， 2012， 52（7/9）：366–374.

[18]張海燕， 郭江峰， 淮秀蘭， 等. PCHE 內軸向導熱對局部換熱性能的影響研究 [J].化工學報 ， 2019， 70（12）：4590–4598.

[19]王績德， 馮巖， 韓東江.超臨界二氧化碳動力循環在鈉冷快堆中的應用綜述[J].核科學與工程， 2019， 39（2）：289–297.

[20] SHI H Y， LI M J， WANG W Q， et al. Heat transfer and friction of molten salt and supercritical CO2 flowing in an airfoilchannelofaprintedcircuitheatexchanger[J].InternationalJournalofHeatandMassTransfer， 2020， 150：119006.

[21]何雅玲， 王文奇， 邱羽， 等.熔鹽在復雜換熱結構內的對流換熱特性實驗研究及進展[J].科學通報 ， 2019， 64（28/29）：3007–3019.

[22] KATO Y， NITAWAKI T， MUTO Y. Medium temperaturecarbon dioxide gas turbine reactor[J]. Nuclear Engineering and Design， 2004， 230（1/3）：195–207.

[23]高毅超 ， 夏文凱 ， 龍穎 ， 等.管徑和轉折角對 Z 型 PCHE 換熱及壓降影響的研究[J].熱能動力工程， 2019，34（2）：94–100.

[24] WANGB，SHENJF，CHENGJD，etal. Numerical improvement using flow and heat transfer calculations of thezigzaggeometryforcarbondioxidePCHEs[J]. Energies， 2022， 15（8）：2831.

[25]顧維藻， 神家銳， 馬重芳， 等.強化傳熱[M].北京：科學出版社， 1990：10.

[26]史以奇， 李凌.螺紋管管內流動與傳熱的數值模擬[J].上海理工大學學報， 2016， 38（2）：133–136，141.

[27] KIMIH，NOHC，LEEJI，etal. Thermalhydraulic performance analysis of the printed circuit heat exchanger usingaheliumtestfacilityandCFDsimulations[J]. NuclearEngineeringandDesign，2009，239（11）：2399–2408.

（編輯：石瑛）