基于自抗擾的永磁直驅伺服電機擾動抑制技術研究

劉 佳,顧毅君,李 朋,顧子杰,董兆鵬,卜飛飛

(1.南京航空航天大學 自動化學院,南京 211106; 2.中國船舶集團有限公司第七二四研究所,南京 211106;3.中國人民解放軍94672部隊,211199)

0 引 言

傳統伺服系統通常采用齒輪、渦輪渦管等機械傳動裝置,存在著齒輪間隙、軸承間隙、彈性形變等影響傳動精度的因素,嚴重影響了伺服轉臺系統的穩態性能[1]。直驅伺服系統去掉了齒輪等中間傳動機構,大大提高了系統的控制精度和響應速度,因此在航空航天、艦載雷達等對伺服轉臺的抗擾動能力和穩定性有較高要求的領域,直驅伺服電機具有廣闊的應用前景。但是,直驅電機和負載直接相連,負載轉矩擾動會直接傳遞給電機,對伺服系統的抗擾動能力提出了更高的要求,如何提升直驅伺服轉臺的擾動抑制能力成為亟需解決的問題[2-3]。

經典PID控制器對負載變化響應速度較差、抗擾動性能差、系統不具備魯棒性,難以滿足直驅伺服系統越來越高的性能要求[4]。重復控制和迭代控制都是針對固定的頻率進行擾動抑制,若系統工況復雜且有較多變化時,擾動抑制效果不強[5-6]。比例諧振控制可以對指定頻率進行擾動抑制,但是控制器環節較多,導致模型復雜,計算困難[7-8]。模糊控制適應性強,擁有良好的容錯性,但是模糊規則的建立需要大量的數據,對計算機性能要求較高,一定程度上限制了它的應用[9-10]。

自抗擾控制(以下簡稱ADRC)不受系統數學模型的影響,原理簡單,適應性強[11-12],對系統內外部擾動均具有較好的調節能力,與 PI控制器相比,在控制精度、抗干擾能力方面都有較大的提高[13-14]。因此ADRC在直驅雷達轉臺等對抗擾動能力要求高的場合受到廣泛關注[15]。

文獻[16]提出一種基于自抗擾的永磁同步電機(以下簡稱PMSM)位置伺服系統,可以有效地抑制外部擾動,但是控制器為非線性結構,參數整定較為復雜。文獻[17]設計了一階轉速環自抗擾控制器實現對電機外環控制,利用擴張狀態觀測器(以下簡稱ESO)對轉矩進行觀測,能夠明顯抑制電機運行過程中的轉矩波動,但是電流環仍采用的普通PI控制,控制精度有待進一步提高。文獻[18]設計了一種基于模糊自抗擾的控制系統,利用模糊控制規則設計非線性狀態誤差反饋,有效地改善了系統控制性能,但是參數調整較為復雜。

基于上述背景,本文設計了一種新型自抗擾控制器,速度環和電流環均采用線性ADRC控制策略。仿真及實驗證明,該控制方案不僅可以明顯抑制轉矩波動,而且電機具有更好的動態響應性能和魯棒性。

1 PMSM以及ADRC的數學模型

1.1 PMSM數學模型

對PMSM數學模型進行分析,本文采用內轉子表貼式PMSM,交直軸電感相同,不計繞組不對稱引發的諧波干擾,忽略磁路飽和,忽略電樞反應,假設電機電阻電感值恒定,PMSM電壓方程可表示[19-20]:

(1)

式中:ud和uq為d,q軸電壓;id和iq為d,q軸電流;p為極對數;ω為轉子角速度;Rs為電阻;ψf為磁鏈;Lq為電機交軸電感。表貼式PMSM的交直軸電感相同,所以轉矩方程和機械運動方程可表示:

(2)

(3)

式中:Te和TL分別為電磁轉矩和負載轉矩;J為轉動慣量;Ba為阻尼系數。

從電機的機械運動方程來看,外部擾動導致的轉矩變化會對轉速產生較大影響,尤其對于直驅伺服系統來說,沒有中間減速緩沖機構,外部擾動會直接作用在電機上,對于電機的穩定運行影響較大,因此,設計合適的控制策略,抑制轉矩擾動,對直驅伺服系統的應用具有重要意義。

1.2 ADRC數學模型

自抗擾控制器主要包括三個環節:追蹤微分器(以下簡稱TD)實現對系統的無超調、高精度的追蹤,并根據輸入的階次,給出相應的微分;ESO觀察系統的輸出,并估計系統的擾動,將系統模型內部參數變化當作內擾,將外部擾動當作外擾,估計出系統總擾動;狀態誤差反饋環節對目標參數進行聯合控制,實現對目標參數的干擾補償[21-22]。ADRC的結構框圖如圖1所示。

圖1中,輸入信號為v,TD設計過渡過程,可以濾除噪聲影響并給出微分信號v1、v2,輸出信號經ESO觀測后得到z1、z2、z3,z3為系統綜合擾動,對系統進行前饋補償,最后將TD和ESO輸出信號作差,經狀態誤差反饋控制和前饋補償一起確定系統的控制量信號。可用如式(4)所示的微分方程描述:

(4)

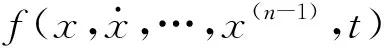
2 轉速環ADRC設計

轉速環是直驅伺服系統設計的重要環節。轉速環對速度進行直接控制,因此不僅要求其對速度控制的精確性,而且還要求其能夠對負荷的改變做出相應的調整。PI控制器可以實現對轉速的控制,但是對于負荷的變化魯棒性不強,影響系統整體性能的提高。因此,以轉速環自抗擾控制器取代常規的PI調速控制器,來增強伺服系統的擾動抑制能力,尤其在負載突加突卸時具有較強的控制性能。

在同步旋轉坐標系下,采取id=0控制策略,PMSM轉速環動態數學模型[24-26]如下:

(5)

式中:ωm為轉子機械角速度;p為極對數;TL為負載轉矩;ψf為永磁體磁鏈;iq為q軸電流。

轉速環自抗擾控制器的設計過程如下:

(1)過渡過程

(6)

(7)

(2)ESO

(8)

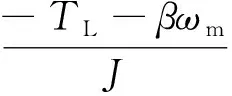
(3)狀態誤差反饋控制率與擾動補償

采用如下線性控制率u0=Kp(v1-z1),其中Kp為控制參數,u0為等效控制量,最終將估計得到的擾動在控制輸入中進行補償:

(9)

以上便是轉速環ADRC的設計過程,其結構框圖和系統控制框圖如圖2、圖3所示。

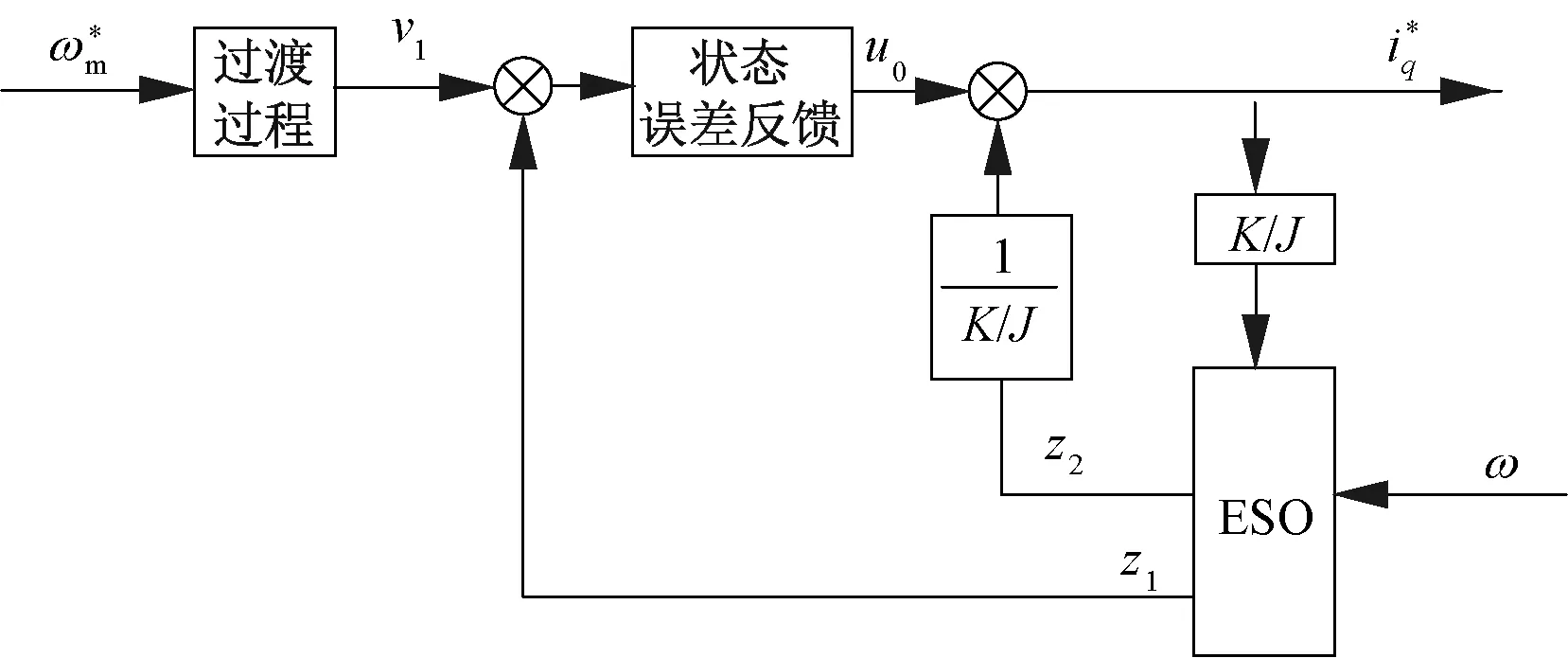
圖2 轉速環ADRC結構圖

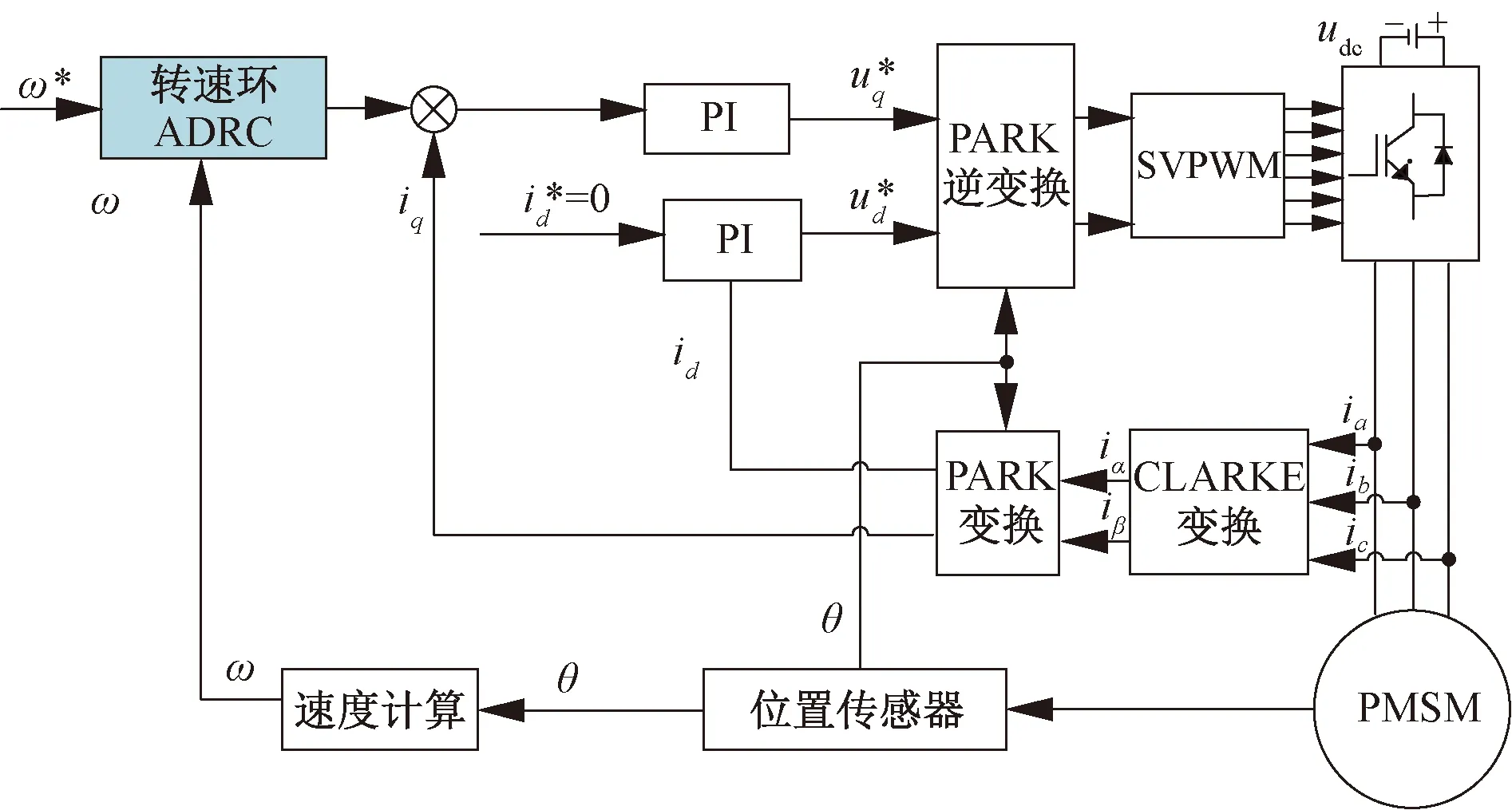
圖3 轉速環ADRC伺服系統控制框圖

3 電流環ADRC設計

在交流伺服控制系統中,對內環電流環的精確控制是實現高精度伺服控制的基礎,電流環應具備良好的瞬態響應和高品質的穩態特性。因此,本文電流環設計了ADRC替代PI控制器,改進了PI控制器的不足,從而使電流環的電流跟隨能力更好,伺服系統整體控制性能更優。

考慮PMSM運動方程和電流方程,獲得如下數學模型[22-23]:

(10)

式中:Ls為d,q軸電感。

(1)過渡過程

對于PMSM直驅伺服系統電流環來說,電流環需要響應較快,因此不設計過渡過程。本文采用id=0控制策略,d軸給定電流為0,q軸參考電流為轉速環的輸出。

(2)ESO

對于d軸電流來講,其電流方程:

(11)

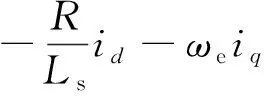
(12)

式中:z2可以觀測d軸總擾動。對于q軸電流來講,其電流方程:

(13)

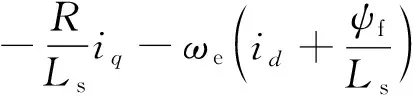
(14)

式中:z2可以觀測q軸總擾動。

(3)誤差反饋控制率與擾動補償

對于d軸電流,id=0,故有:

u0=kp(0-z1)

(15)

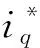
(16)

最后,將估計的擾動在控制輸入中進行補償:

(17)

其結構圖和控制框圖如圖4、圖5所示。

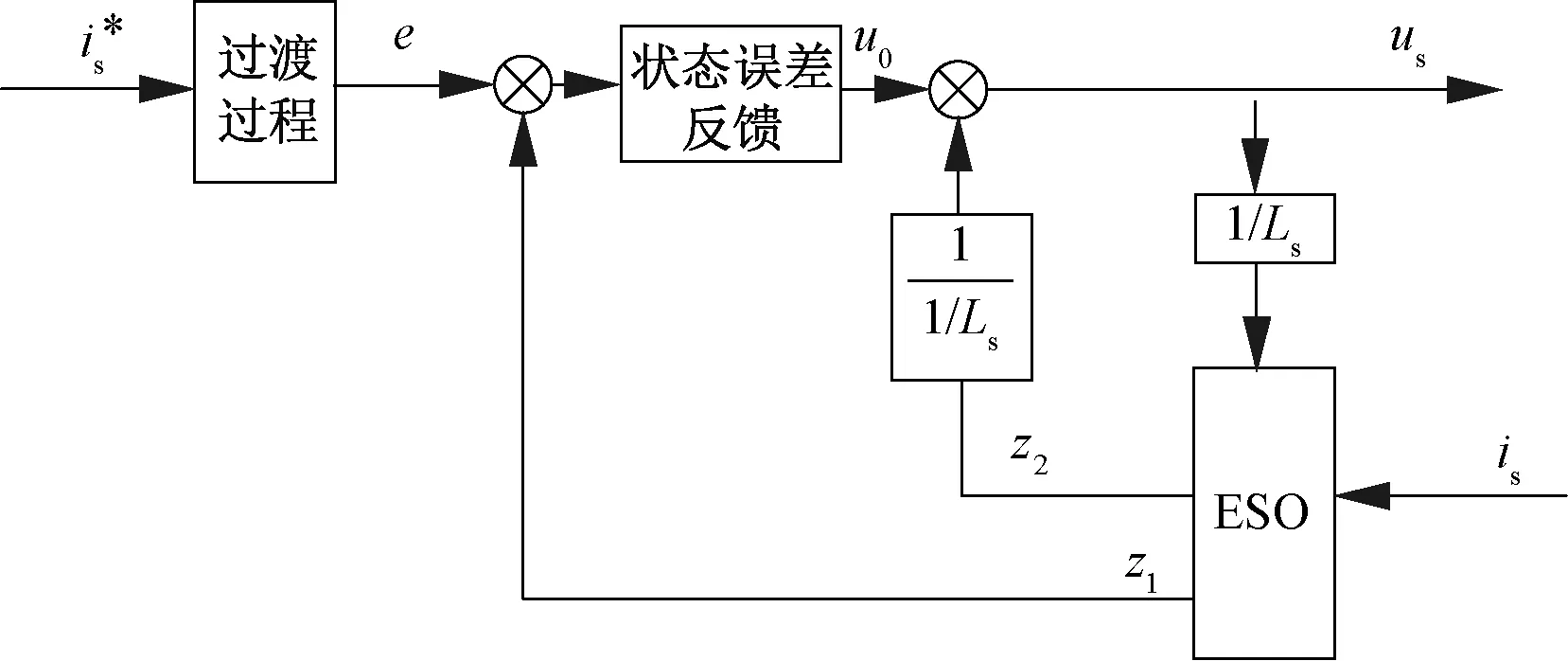
圖4 電流環ADRC結構圖

圖5 轉速電流雙環ADRC系統控制框圖

4 仿真與實驗

4.1 仿真驗證

為驗證本文的永磁直驅電機自抗擾控制策略,在MATLAB/Simulink中搭建模型,對傳統PI控制器與本文設計自抗擾控制器進行仿真對比與實驗對比。表1為本文所用電機的各項參數指標。

表1 仿真與實驗平臺參數

電機以1 000 r/min的轉速空載運行,在0.2 s時對電機突加0.2 N·m負載,觀察電機轉速以及電流變化情況,仿真結果如圖6所示。

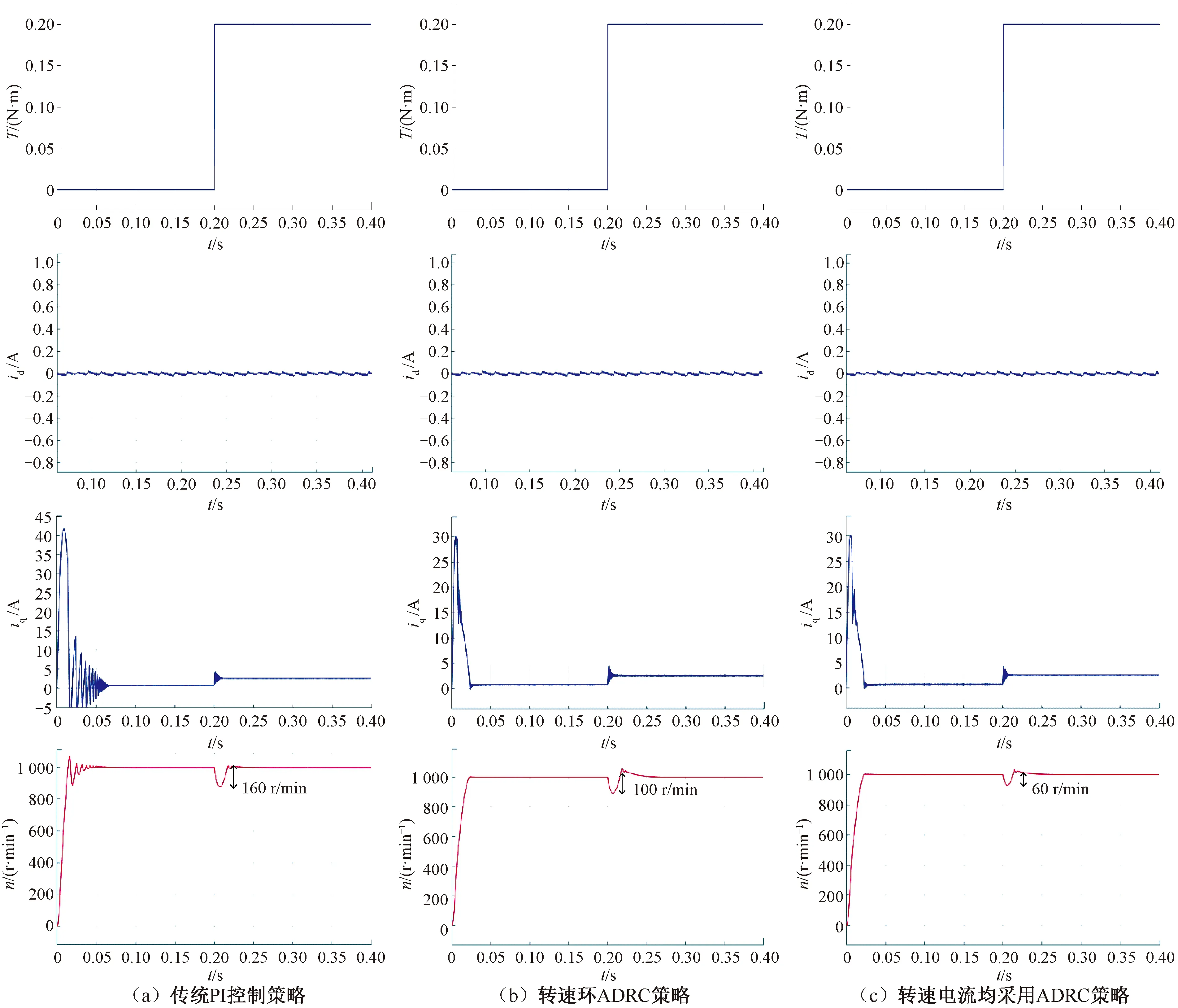
圖6 不同控制策略下突加載仿真結果對比

圖6(a)為采用傳統PI控制時電流和轉速的變化曲線,圖6(b)為轉速環采用ADRC時電流和轉速的變化曲線,圖6(c)為轉速電流環均采用ADRC時電流和轉速的變化曲線。從圖6可以看出采用傳統PI控制策略時,轉速跌落160 r/min左右,采用轉速環ADRC控制策略時,轉速跌落約100 r/min,在轉速電流環都采用ADRC控制策略時,轉速跌落約60 r/min,電機轉速波動得到明顯的抑制,有效提升了電機運行時的魯棒性。仿真結果證明,本文的ADRC策略可以有效實現對擾動轉矩的抑制作用。

4.2 實驗驗證

為了進一步驗證ADRC策略的有效性,采用如圖7所示的對拖實驗平臺進行實驗測試。實驗平臺參數如表1所示,由一臺驅動電機和一臺負載模擬電機組成。控制器硬件主要包括主功率電路、保護電路、DSP控制電路等。

圖7 實驗平臺實物圖

對電機擾動抑制策略進行驗證。先起動電動機,然后利用負載電機進行加載,給定負載0.2 N·m,觀察加載前后轉速波動變化。在相同給定條件下對PI控制策略,轉速環ADRC策略和轉速電流均采用ADRC策略進行對比實驗。

圖8給出了采用三種不同控制策略突加載時,電機的轉速電流變化結果。可以看到,PI控制策略下,加載時電機的轉速跌落約為110 r/min,而在轉速環單獨采用ADRC策略時,電機的轉速跌落約為80 r/min,相比之下電機受擾動影響得到一定程度的抑制,但是依然有比較大的轉速跌落情況。為提高系統響應速度和跟蹤精度,進一步設計了電流環ADRC,實驗結果表明,在相同的負載擾動條件下,轉速、電流環均使用ADRC策略時轉速跌落只有50 r/min左右,電機轉速波動得到了更為有效的抑制。

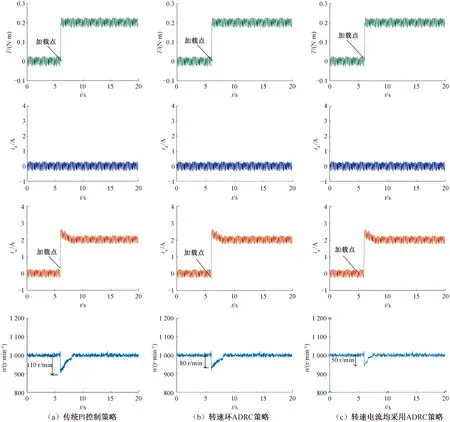
圖8 不同控制策略下突加載實驗結果對比

5 結 語

本文設計了永磁直驅電機的自抗擾控制器,首先設計了轉速環自抗擾控制器,通過ESO以及誤差反饋補償,提高了電機對轉矩擾動的的抑制能力;同時,針對PI調節器中電流環d,q軸耦合無法實現對電流指令準確追蹤的問題,進一步設計了電流環ADRC,可以對轉速環的輸出電流指令進行快速準確的追蹤,使得系統響應時間縮短,在負載突變后具有更快的響應速度,從而提升系統擾動抑制能力。獲得以下結論:

1)通過對轉速環自抗擾控制器的設計,提升了系統的擾動抑制能力,提升了速度控制的平穩性。

2)通過對電流環自抗擾控制器的設計,提升了對q軸電流的跟蹤精度和準確度,加快了系統的響應速度,在應對外部擾動時,具有更好的魯棒性。

3)仿真與實驗證明,本文的永磁直驅電機ADRC策略是有效可行的,可以明顯改善外部擾動下系統速度控制的平穩性。