小學低段學生幾何思維的進階路徑

馬曉丹　趙星玉

摘要 在小學低段幾何教學中促進學生幾何思維從直觀水平向描述、分析水平發(fā)展是必要的。低段學生幾何思維的進階路徑包括三個階段：一是接收外界刺激階段，借助多種感官發(fā)展學生直觀水平；二是信息的編碼與存儲階段，借助比較和分類發(fā)展學生描述水平；三是信息的提取階段，借助想象發(fā)展學生分析水平。

關? 鍵? 詞 幾何思維 直觀水平 描述水平 分析水平

引用格式 馬曉丹，趙星玉.小學低段學生幾何思維的進階路徑[J].教學與管理，2023（29）：31-33.

隨著數(shù)學學科專業(yè)化程度的不斷提升，數(shù)學思維表現(xiàn)出越來越強的學科特殊性，并逐步形成了一些獨有的思維形式，幾何思維就是數(shù)學學科的重要概念性思維之一[1]。數(shù)學教育家范·希爾夫婦提出的幾何思維發(fā)展理論是具有典型意義的幾何思維研究之一，該理論將幾何思維劃分為直觀、描述/分析、抽象/關聯(lián)、形式推理、嚴密性/元認知五個水平，一些學者還在這五個水平之前設置了前認知水平。幾何思維的發(fā)展貫穿于整個數(shù)學學習的進程，其中“直觀”是小學低段幾何學習需要重點發(fā)展的思維能力，但這一學段的學生不應該止于直觀。正如鄭毓信教授指出：“如果小學生的幾何學習始終停留于所謂的直觀幾何，也就是圖形的直觀感知，卻沒有認識到必須超越直觀深入地去研究各個圖形的特征和相互聯(lián)系，這將被看成是一種‘淺度學習。”[2]在低段數(shù)學教學中，促進學生幾何思維從直觀水平向描述、分析水平發(fā)展是必要的。

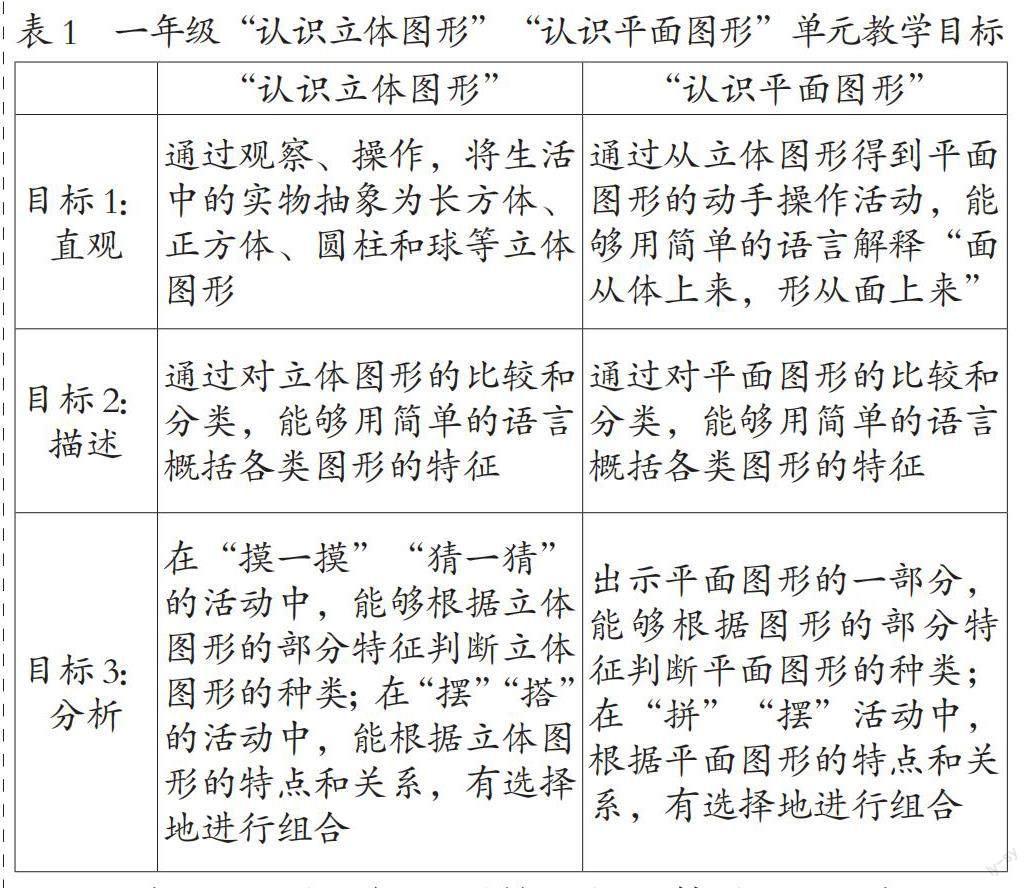
學生在一年級上學期和下學期分別認識立體圖形和平面圖形。從內容進階的角度來看，學生需要經歷由體到面，由整體到部分的認識過程。從幾何思維進階的角度看，學生認識立體圖形和平面圖形的過程都遵循著直觀、描述、分析三個層次。為探索低年級學生幾何思維進階的實施路徑，筆者從這兩個單元的教學目標（見表1）展開討論。

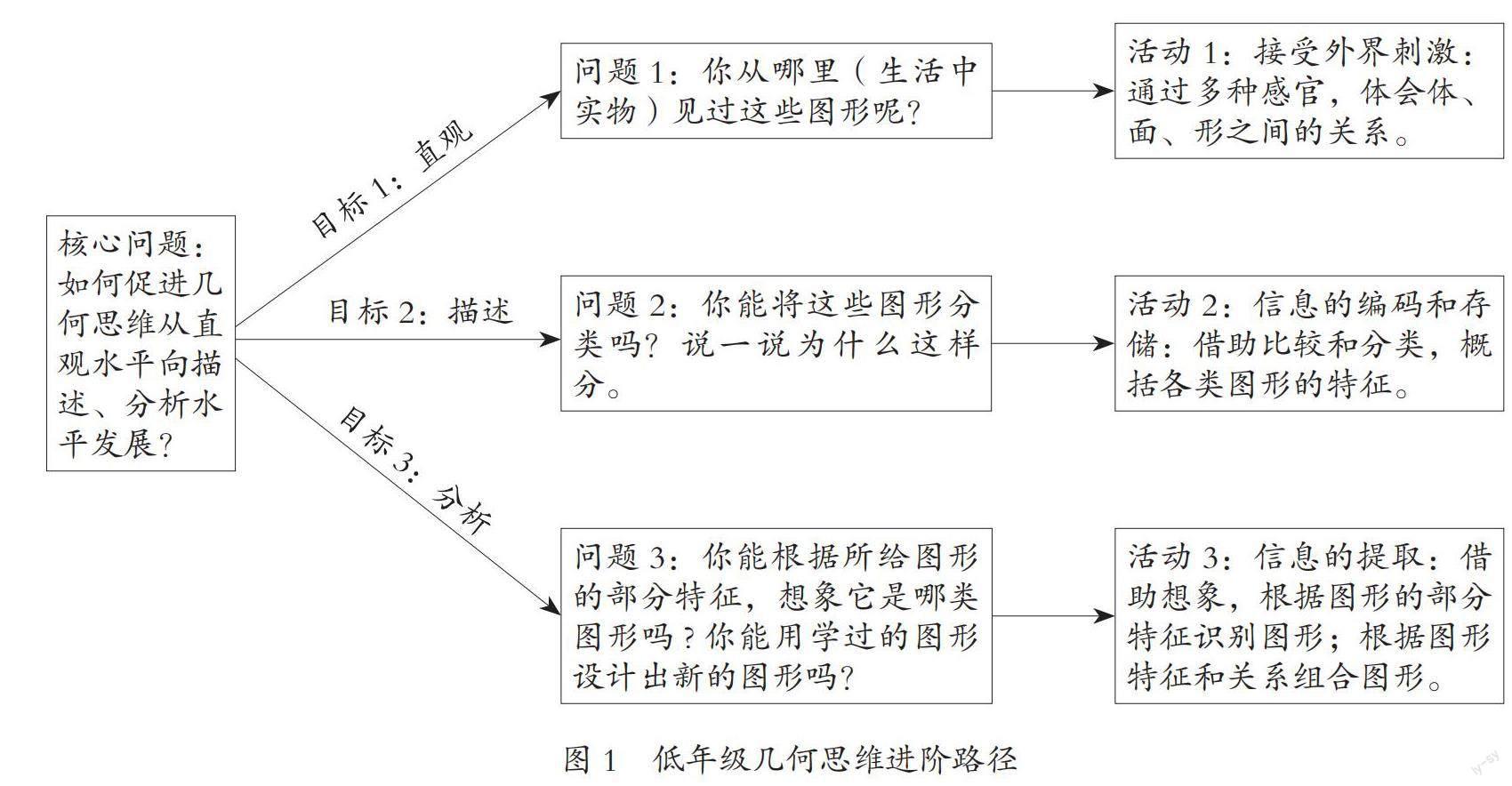
目標1是對幾何圖形外觀的整體認識，目標2是對圖形特征的理解，目標3是根據圖形的部分特征對圖形整體的識別。目標1—3分別對應幾何思維的直觀化水平、描述水平和分析水平，在達成的順序上遵循幾何思維進階的順序。每一項教學活動的設計都以幾何思維的層層遞進為目的（如圖1）。活動1借助多種感官接收外界刺激，以實現(xiàn)幾何思維直觀化；活動2在比較和分類中，對信息進行編碼和存儲，以實現(xiàn)幾何思維的描述水平；活動3借助想象促進信息的提取，以發(fā)展學生的分析水平。

一、接收外界刺激：借助多種感官發(fā)展學生直觀水平

兒童在達到直觀化水平之前，只能根據平面圖形和對應立體圖形的某個相似點，片面地對圖形類別作出判斷，表現(xiàn)為不能區(qū)分平面圖形和其對應的立體圖形。例如，混淆長方形和長方體、圓和球等。小學低段學生的幾何學習需要借助手、眼、口、腦等身體感官發(fā)展其直觀水平。這是信息加工的初始階段，即通過觸覺、聽覺、視覺等接收外部環(huán)境中的刺激。弗賴登塔爾稱之為“直觀感知的低層次活動”，其目的是“讓學生用肉眼觀察，借助手腦并用，進而將物體現(xiàn)實抽象為幾何對象”[3]。

在“認識立體圖形”單元中，學生從生活中的實物出發(fā)，通過看、摸、推、滾等方法，整體感知物體的幾何屬性，忽略顏色、圖案、功能等非幾何屬性。在“認識平面圖形”單元中，學生將注意力聚焦到立體圖形的平面上，通過“描”或“印”的方法將立體圖形上的平面“繪制”在紙面上。學生借助多種感官進行觀察、操作，所積累的活動經驗為建立立體/平面圖形的類屬關系做準備。

學生在直觀水平上經歷的轉化是雙向的：一方面是現(xiàn)實生活向數(shù)學世界的轉化，另一方面是數(shù)學世界向現(xiàn)實生活的轉化。教師不僅可以提問“保溫杯的形狀是怎樣的？”“牙膏盒上各個面的形狀是什么樣的？”還可以提出“生活中還有哪些物品是這樣的形狀？”“你從生活中的哪一件物品上看到過這樣的面？”等問題。此時，學生逐漸降低多種感官的依賴，通過回憶、再認等行為發(fā)展更高層次的幾何思維。

二、信息的編碼與存儲：借助比較和分類發(fā)展學生描述水平

小學低段學生的幾何學習需要在直觀水平的基礎上發(fā)展為描述水平，具體表現(xiàn)為能夠概括出圖形的特征，能夠根據特征對圖形進行分類。類屬關系的形成標志著學生已有知識結構的重組和改建，此時學生接收的外部信息不再是一個一個的獨立事件，而是以結構化的方式重新編碼，以“類”的形式存儲在長時記憶中。

分類是數(shù)學抽象的基礎，比較為分類提供依據。在比較和分類的過程中，圖形本質屬性的清晰化是形成具體概念的基礎。在“認識立體圖形”單元，教師引導學生比較球、圓柱、長方體和正方體的特征，并嘗試進行分類活動。學生首先在直觀操作的基礎上，根據“能否滾動”將球、圓柱與長、正方體區(qū)分開來；進一步，根據“有無平面”將圓柱和球區(qū)分開，再根據“面的特點”將長方體和正方體區(qū)分開。

類似地，在“認識平面圖形”單元，教師引導學生比較長方形、正方形、三角形和圓的特征，并嘗試進行分類活動。通過觀察，學生首先根據“有無曲邊”或者“有無角”，將圓與其他圖形區(qū)分開；再根據“邊的數(shù)量”或“角的數(shù)量”將三角形與長方形、正方形區(qū)分開；進一步，根據“方方正正”這一特點將正方形和長方形區(qū)分開。教師通過發(fā)起生生互動和師生互動，引導學生在比較的基礎上區(qū)分，讓每位學生嘗試描述分類背后的依據。

一年級不要求掌握圖形的具體概念，學生對圖形特征的描述多是運用兒童自己的語言，比如“立得住的”“平平的”“尖尖的”“方方正正的”等等。分類是信息加工的一種方式，更是一種數(shù)學思想方法。“分一分”活動使學生頭腦中已有的關于立體圖形或平面圖形的“印象”更加清晰化，學生能用自己的語言描述圖形間的相同點和不同點，為今后形成圖形概念做準備。

三、信息的提取：借助想象發(fā)展學生分析水平

小學低段學生需要進一步發(fā)展幾何思維的分析水平，具體表現(xiàn)為根據圖形的特征識別圖形和圖形組合，這一過程涉及到信息的提取。信息的提取是對儲存在長時記憶中的信息的回憶和再現(xiàn)。信息能否被快速、準確地提取與信息的存儲方式有密切聯(lián)系。相對于碎片化的信息，結構化的、整合后的信息更容易被提取。也就是說，信息的編碼和存儲對信息的提取至關重要。在信息提取的過程中，教師可以引導學生借助想象，增加學生信息提取的線索，排除相似刺激帶來的干擾。

比如，教師可以設計“根據局部特征想象圖形全貌”的活動，逐次提供有關圖形特征的信息，引導學生對圖形展開猜想和驗證。在“認識立體圖形”單元，教師可以提供立體圖形的部分特征，學生根據信息“圓圓的”，排除掉長方體、正方體這兩種不符合信息的立體圖形，學生根據補充信息“上下一樣粗”，鎖定圓柱這一立體圖形。

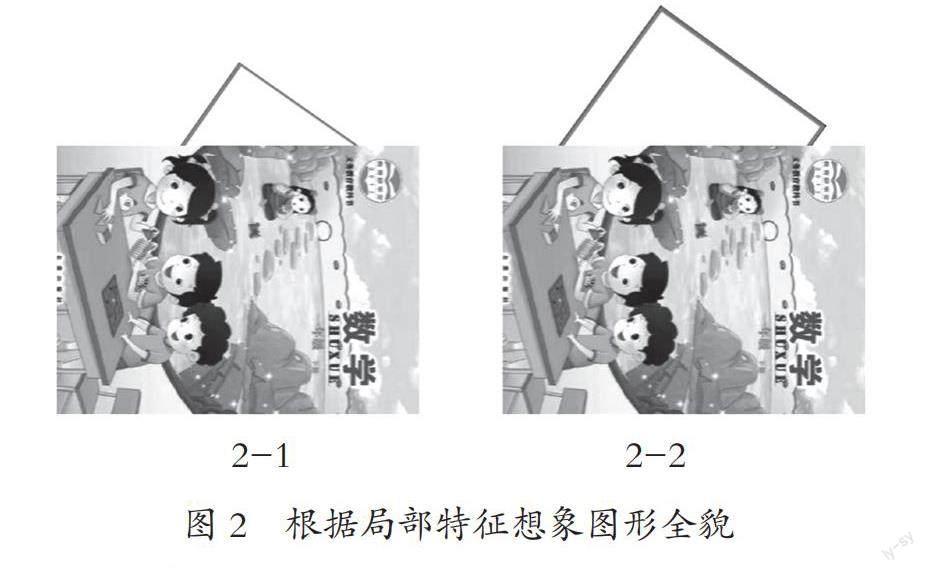
類似地，在“認識平面圖形”單元，教師同樣可以提供平面圖形的部分特征，比如用書本擋住圖形的一部分。學生根據信息（圖2-1），提出自己的思考“一定是三角形嗎？”“還有哪些圖形有這樣的角呢？”緊接著，教師讓擋住的圖形多露出一部分，學生根據補充信息（圖2-2），排除掉“三角形”，并引發(fā)持續(xù)的思考“一定是正方形嗎？”“還有可能是哪些圖形呢？”

此外，根據圖形特征對圖形進行組合也是幾何思維達到分析水平的表現(xiàn)。例如，人教版和北師大版教材都設計了“搭積木”和“七巧板拼擺”的活動。學生并非停留在圖形的直觀表征上，而是提取有關圖形點、線、面特征的信息，將合適的立體/平面圖形組合在一起，借助想象創(chuàng)造出多種可能的組合。

范·希爾夫婦認為，決定學生幾何思維發(fā)展的主要因素不是年齡，而在很大程度上依賴于教師的課程[4]。“認識立體圖形”和“認識平面圖形”兩單元的課程建構正是遵循了學生幾何思維的進階規(guī)律。兒童并不是“讀出”他們的空間環(huán)境，而是通過主動操作周圍環(huán)境中的形狀，建構他們對圖形的認識[5]。多種感官的使用，以及比較、分類和想象等方法的運用有效促進了低年級學生的幾何思維進階。值得注意的是，學生在一年級達成的描述和分析兩個層次的幾何思維需要在高年級給予持續(xù)的關注。當學生在中、高學段再次學習長方形、正方形、三角形和圓時，學生在描述和分析水平上的表現(xiàn)會得到進一步深化。以三角形為例，學生超越了“三條邊”和“三個角”的描述，形成了具體的數(shù)學概念（由三條線段順次首尾相接組成的圖形），學生對三角形的分析不再局限于外部特征的分析，而是基于三角形的穩(wěn)定性（定性的）和三邊關系（定量的）展開討論。此外，學生的幾何思維還將在有關周長、面積的學習中，向更高層次的抽象、關聯(lián)和推理水平發(fā)展。

參考文獻

[1] 鄭毓信.數(shù)學思維與小學數(shù)學[M].南京：江蘇教育出版社，2008：66.

[2] 鄭毓信.數(shù)學深度教學的理論與實踐[M].南京：江蘇教育出版社，2020：139.

[3] 弗賴登塔爾.作為教育任務的數(shù)學[M].陳昌平，唐瑞芬，等譯.上海：上海教育出版社，1995：278.

[4] 鄭毓信.小學數(shù)學教育的理論與實踐[M].上海：華東師范大學出版社，2017：150.

[5] 克萊門茨，薩拉馬.兒童早期的數(shù)學學習與教育：基于學習路徑的研究[M].張俊，陶瑩，李正清，等譯.北京：教育科學出版社，2020：217.

［責任編輯：陳國慶］