基于與異或非圖的混合粒度可重構密碼運算單元設計

戴紫彬 張宗仁*② 劉燕江 周朝旭 蔣丹萍

①(解放軍信息工程大學 鄭州 450000)

②(31642部隊 臨滄 677000)

1 引言

信息安全在互聯網、物聯網中越來越重要，而密碼算法是保證信息安全的關鍵手段[1]。其中對稱密碼分為序列密碼和分組密碼，由于多種對稱密碼的基本編碼環節具有相似性，適用于可重構實現[2]。

粗粒度可重構密碼邏輯陣列(Coarse-Grained Reconfigurable Cipher logic Array, CGRCA)根據密碼算法的計算特征，在高性能和高靈活性之間達到平衡，ANOLE[3]是面向分組密碼的高性能流水處理架構，采用查找表(LookUp Table, LUT)和寄存器的方式實現序列密碼算法中反饋移位寄存器(Feedback Shift Register, FSR)的狀態更新，但支持的序列密碼算法較少，性能不高。PVHArray增加了專用的非線性反饋移位寄存器(Nonlinear Feedback Shift Register, NFSR)處理電路和FSR，但其處理粒度基于字，在實現序列密碼的單比特更新時，高位計算資源被閑置，同時陣列在處理分組密碼時，專用NSFR電路基本閑置，硬件資源利用率較低[4]。文獻[5]提出一種面向序列密碼的混合粒度并行運算單元，兼容多種粒度的序列密碼算法，同時采用并行抽取和流水線設計提高了密碼算法的處理性能。該單元提升了CGRCA對序列密碼的兼容性，但仍然增加很多專用FSR的電路，硬件資源利用率低。文獻[6]提出了一種可重構多發射流水處理架構，但是這種架構容易產生流水線的結構沖突，從而極大程度上限制了粗粒度可重構邏輯陣列的性能。綜上，現有的面向對稱密碼算法的CGRCA，對序列密碼兼容性較差、資源利用率低。

目前，國內外針對FSR進行一些可重構設計。徐光明等人[7]提出一種基于LUT的可重構NFSR處理結構，基礎模塊是支持任意6變量布爾函數的高級非線性邏輯單元(Advanced Nonlinear Logic Unit,ANLU)，該單元靈活性高，配置量少，硬件開銷小，但性能和硬件資源利用率仍然較差。Nan等人[8]提出將NFSR、線性反饋移位寄存器(Linear Feedback Shift Register, LFSR)和有限域乘法相融合的可重構單元，提升了硬件資源利用率。文獻[9]以提高資源利用率為目標，以變量頻次為約束改進適配算法，并設計單元互聯結構，將資源利用率提高到91%以上。針對多功能融合的可重構單元，目前研究主要集中于對單一功能下的多種操作位寬設計的可重構[10,11]單元，以及用復選器進行功能重構的可重構單元。另外對于多功能實現往往是對單一功能的選擇控制實現，流水線處理時會面臨同一時刻要使用同一功能單元的情況，而此時，必然會有大量未使用功能單元閑置，功能單元的競爭沖突會同時帶來性能和資源利用率降低。因此，設計可重構的多功能混合粒度的運算單元是解決細粒度的序列密碼算法兼容性差，和流水線處理時功能單元競爭沖突問題的可行方案。

綜合分析序列密碼和分組密碼中不同編碼環節特點，分析得出電路同構部分，結合與-異或-非圖(And-Xor-Inv Graph, AXIG)在邏輯綜合上的優勢，主要做出以下3個方面貢獻：(1)提出可重構邏輯元件(Reconfigurable And-Xor-Nand, RAXN)，該元件可用于AXIG，可同時實現3項基本邏輯功能。另外，提出了RAXN的晶體管級方法并設計了版圖，延遲性能較傳統方法均有明顯提升。(2)提出基于RAXN邏輯元件的多功能擴展方法，設計了多功能單元節點—RAXN-U，可重構實現全加器、3輸入與異或邏輯、乘法部分積生成、可重構非線性布爾函數等功能節點。(3)提出一種面向粗粒度可重構陣列的可重構單元的互聯結構，在CGRCA平臺上可用于實現32 bit加法、8 bit乘法、CF(28)有限域乘法、非線性布爾函數等多項核心運算。

所提運算單元較為規整，可擴展性較強，非線性布爾函數的擴展只需改變互聯節點配置，其他功能只需要增加少量控制電路，即可滿足序列密碼算法和分組密碼算法的多種功能運算和多種位寬的需求。此單元將非線性布爾函數功能的延遲降低了1.27 ns，同時可以緩解電路資源閑置問題以及流水線處理時部分功能單元競爭沖突問題。

2 基于AXIG的可重構邏輯元件設計

2.1 AXIG理論與研究動機

邏輯綜合是數字電路設計中非常重要的部分，選擇不同的邏輯表達范式，綜合優化后的電路在面積、性能、可測試性和可靠性上會有較大差別[12]。由于CMOS電路在可靠性、靜態功耗以及設計復雜度等方面擁有顯著優勢[13]，傳統布爾邏輯(Traditional Boolean, TB)得到廣泛運用。而以And-Xor為原語的里德穆勒(Reed-Muller, RM)邏輯設計電路，可以使實現算術運算和奇偶校驗函數更為簡單，在面積、延遲和功耗上都有明顯的優勢。但用RM邏輯表達“或(OR)”邏輯時，需要較復雜的結構，因此和RM邏輯混合的AXIG有更大的優化效果[14]。目前針對AXIG的研究主要是在邏輯級或算法級對電路進行面積、延遲和功耗的優化，在晶體管級研究較少，文獻[15]設計了基于RM邏輯的3輸入AND/XOR門，在面積、功耗上相比傳統的AND門-XOR門級聯結構有明顯優勢，將該復合門運用到操作位寬可配置的乘法電路中，功耗和延遲有較大提升，但未有相關研究在晶體管級設計實現AXIG的基本單元。

本文設計一種可配置實現“與、異或、與非”邏輯的元件RAXN，其中AXIG中的“非(Inverter,Inv)”原語可以利用“與非”邏輯得到，因此可以根據需求，將RAXN作為基本邏輯單元，配置成為最優的AXIG，以充分利用其在復雜非線性布爾函數和算術電路中的優勢。

2.2 RAXN邏輯元件晶體管設計

當M=0, C=0時，F=1。電路中Y和F的邏輯表達式分別如式(1)、式(2)所示

同時將信號M，或者A, B, C中的一個信號當作配置信息時，輸出F可同時實現“And, Nand,Xor”，此3個邏輯正是雙邏輯范式最基本的3個原語(And, Inv, Xor)。

2.3 RAXN邏輯元件延遲分析與版圖實現

由圖1可知，M=1, C=1，當電路輸出為“Xor”邏輯時，若B=1, P1, P4, P5均是關斷狀態，則前一級上拉電路無法形成通路，N2, N3, N4均是導通狀態，前一級下拉電路中形成如圖1紅線所示的信號通路。Y此時輸出為0，則后一級中P9導通，N7關斷；又因為此時P7, P8, P10是關斷狀態，N6,N7, N10是導通狀態，則此時電路相當于信號A的反相器，A的翻轉信號傳到F需要經過P6, P9或N10, N8, N6(紫色線路部分)。若B=0，同理分析可得，A的翻轉信號需要經過P5, N7到F，或者經過N5, N2, P9到F，即下降沿經過2個晶體管，上升沿經過3個晶體管。同理可得如表1所示為每個信號的翻轉時信號傳輸路徑。C的信號傳輸路徑最短，B,A的最差情況一樣長，但A的平均信號傳輸路徑比B短。

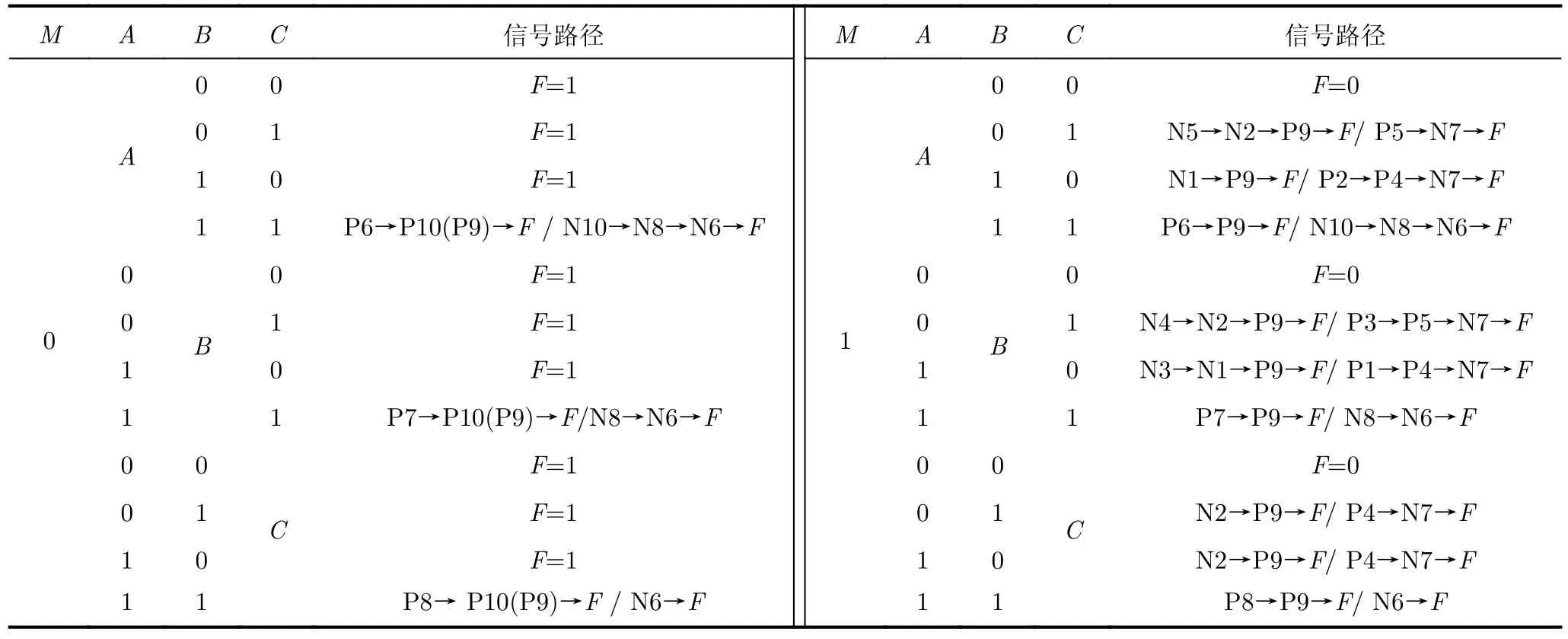
表1 RAXN電路信號傳輸路徑分析

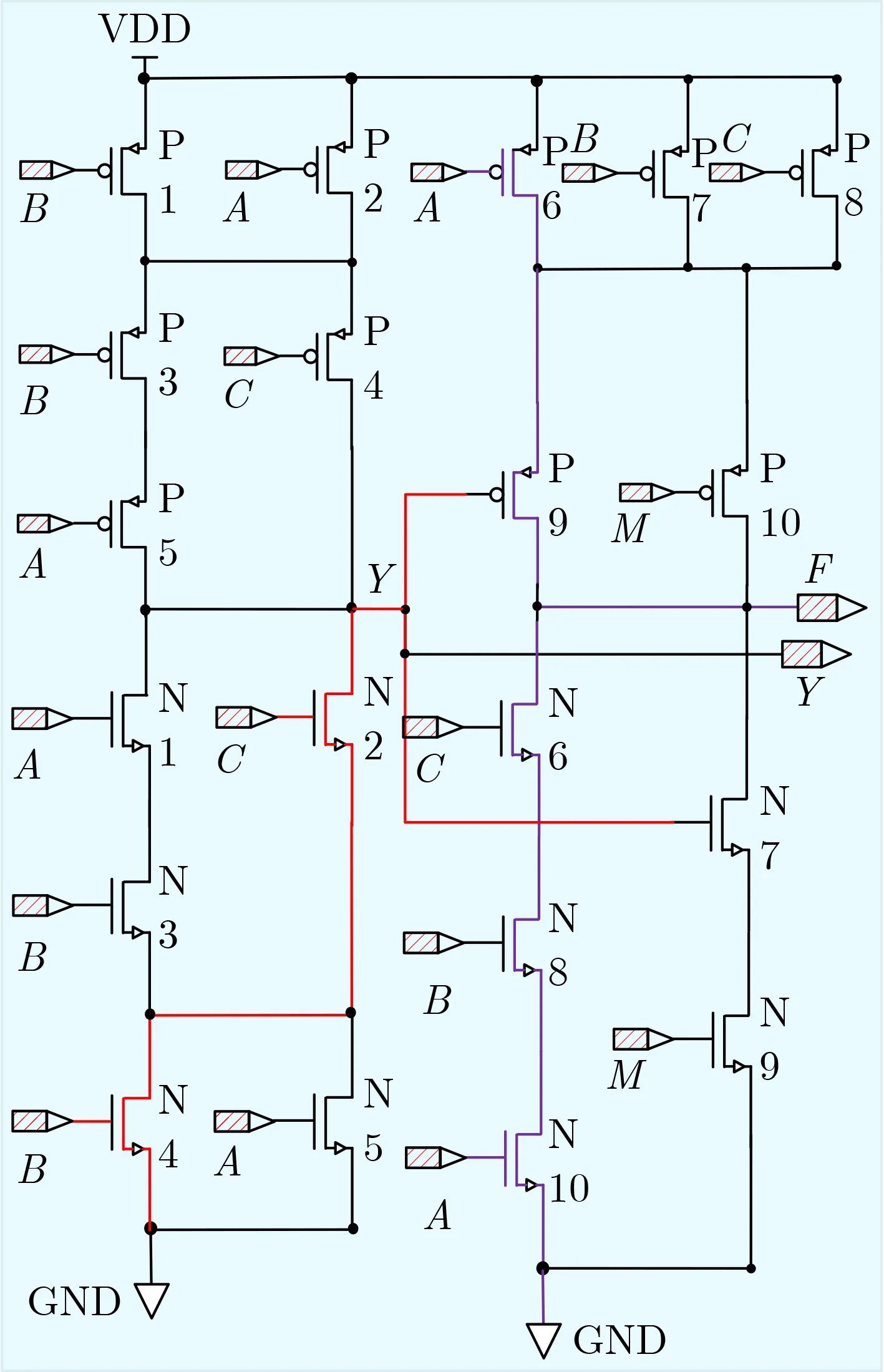
圖1 RAXN晶體管級實現

根據以上分析，關鍵路徑的信號從C端口輸入時可以減少電路延遲，同時調整關鍵路徑上的晶體管寬長比P5, P9, P10, N1, N2, N6, N7，減小單元的延遲。對于非關鍵路徑上的晶體管可以采用高閾值的晶體管，以降低功耗，圖2為其最小驅動能力下的版圖設計。

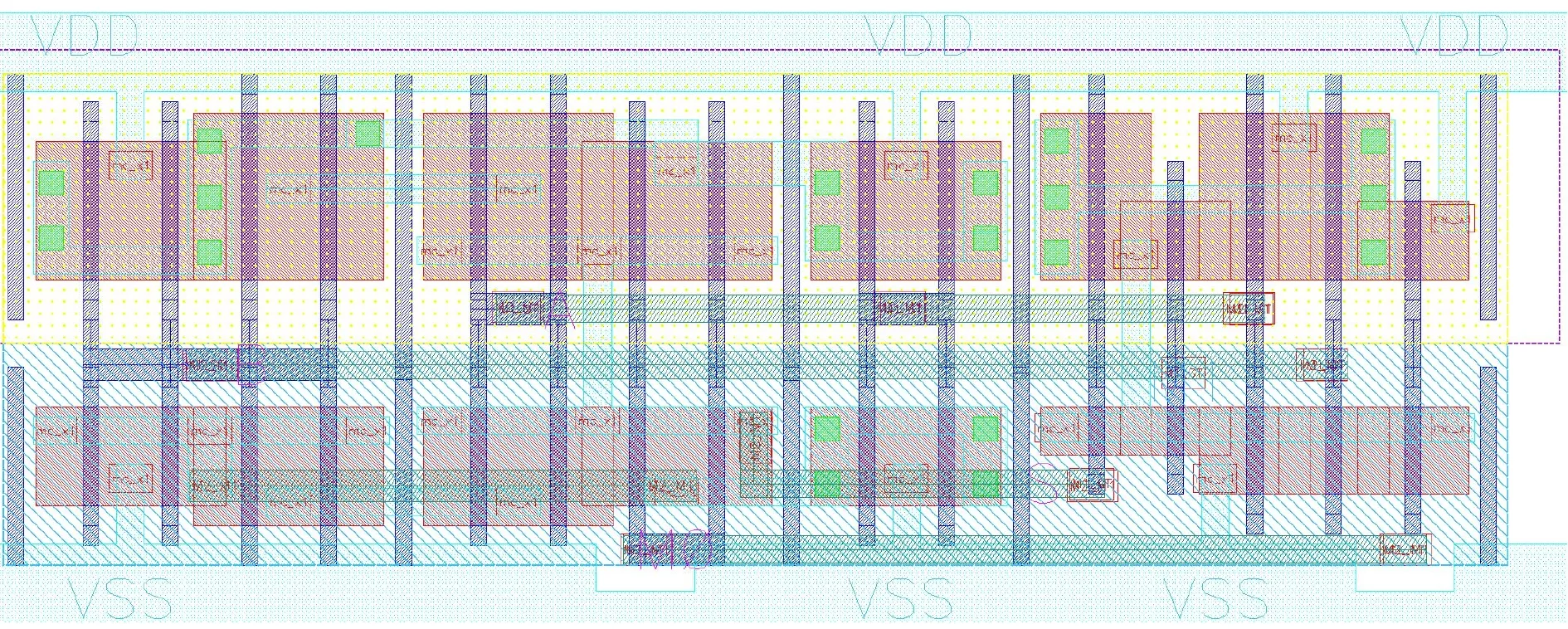
圖2 RAXN的版圖設計

3 基于RAXN的密碼運算單元分析

3.1 密碼算子特征分析

對稱密碼算法是基于特定的密碼學性質而設計的，因此不同的對稱密碼算法具有相同的基本操作成分，其中出現頻次出現最多的是：異或、移位、置換、非線性(線性)布爾函數、S盒、有限域乘法和算術運算。

從本質上講，所有的編碼環節都是布爾函數操作，布爾函數又各有特點，比如序列密碼中單比特為操作位寬的非線性(線性)布爾函數，特點是輸入變量多，形式復雜多樣；以字為操作位寬的序列密碼和分組密碼中S盒、置換、移位為多輸入多輸出，輸入多為8, 16, 32等字節的倍數，輸出有4, 8, 16等特定位數，有限域乘法主要集中CF(28)上，多以矩陣乘法形式出現，算術運算在密碼學中使用模加、模減、模乘，位寬主要為16 bit和32 bit。因此設計一種位寬為8的基本單元，利用CGRA中數據抽取和數據分配電路，擴展至16, 32等位寬，同時實現多類操作，可極大提高資源利用率和單元的靈活性。本文重點討論非線性布爾函數(S盒)、有限域乘法、算術運算這3類算子如何重構到同一單元中。

3.2 基于RAXN的3類密碼算子設計分析

目前，對非線性布爾函數和S盒的研究主要是利用LUT的級聯組合來實現，但LUT的靈活性過強，在特定領域中應用時會造成比較大的資源冗余[16]。2012年，瑞士聯邦理工學院提出一種基于“與非錐(And-Inv-Cones, AIC)”的布爾函數實現方式，在處理大位寬輸入的函數時有較為明顯的面積和延遲優勢[17]，但其“And-Nand”并不適合處理“異或”運算，針對密碼學中非線性布爾函數異或邏輯較多的特點，本文提出一種“與-異或-與非錐(And-Xor-Nand Cones)”的網絡(如圖3)，節點采用本文設計的可重構邏輯元件RAXN，其中上一級輸出接入下一級的A, B端口，C, M端口分別接配置信息di,di+1，輸出端口F輸出信號O，作為下一級的輸入和全局輸出。每個節點可以配置為“And,Nand, Xor, 1”4個邏輯，可以更好地支持“異或”運算；當第3級的一個輸入端口需要置1時，只需將第2級相應節點的配置信息di,di+1全部置0即可，這樣此節點的上一級節點仍然可以獨立執行功能，避免了一條完整分支全部置1造成的資源占用。

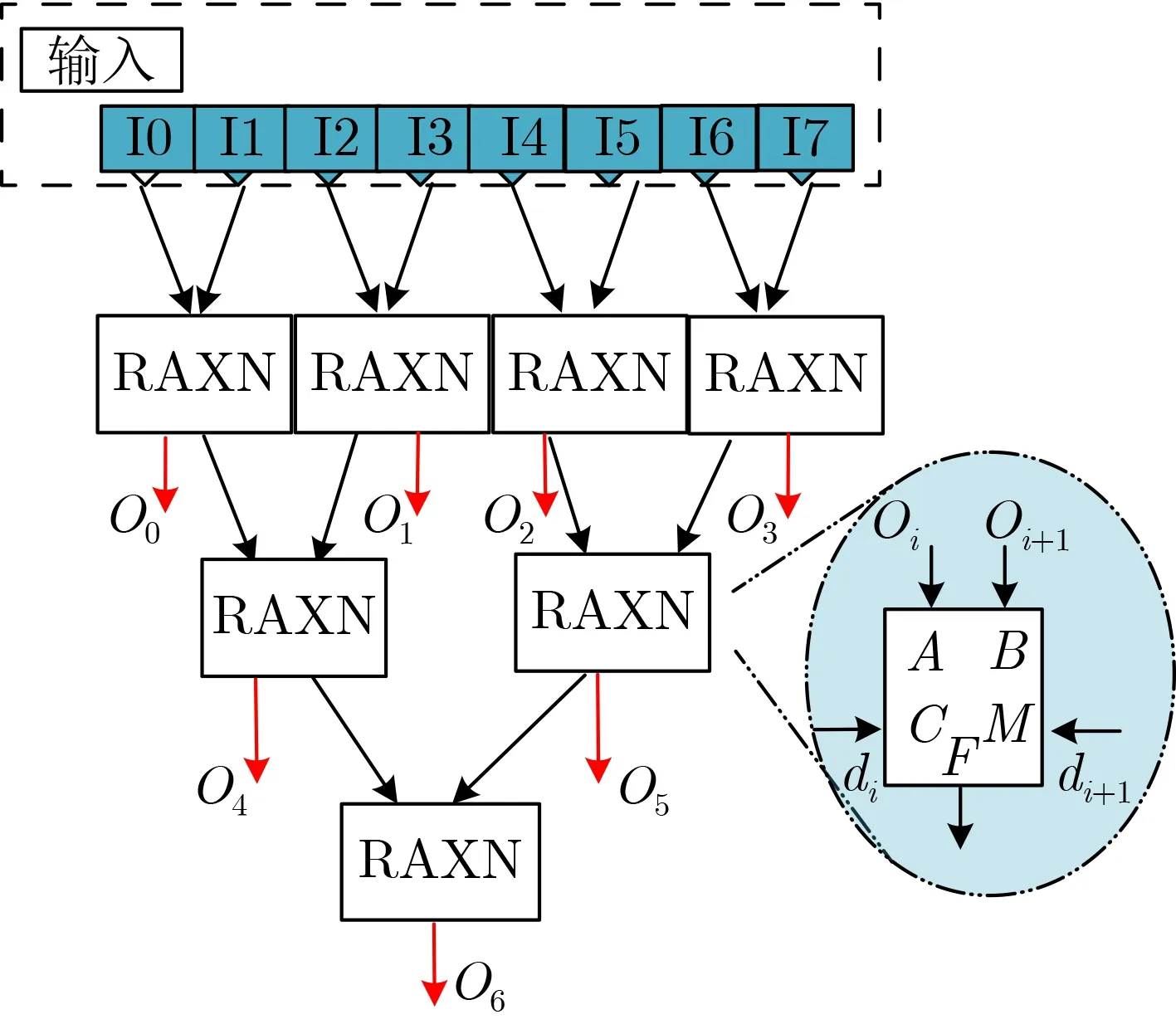
圖3 “與-異或-與非錐”3級深度的互聯結構

有限域乘法主要出現在分組密碼中多維尺度變換(Multi-Dimensional Scaling, MDS)矩陣乘法，序列密碼算法中Fibonacci LFSR并行更新、Galois LFSR并行更新，以及基于字的序列密碼中復合域乘法等編碼環節中。相關研究總結出CF(28)域上乘法的基本電路結構，由兩級運算電路，一級為冪乘(Xtime)電路，一級為“與-異或”的陣列[6]。“與-異或”的陣列可以用圖3結構實現，Xtime結構是由3輸入函數FX=hf ⊕a級聯組成。其中f[7:0]是不可約多項式的系數，a[7:0]和b[7:0]是CF(28)域上的兩個元素，若A=M=a,B=h,C=f，則根據式(5)可利用RAXN作為FX的實現電路

4 基于RAXN的可重構多功能密碼運算單元設計

4.1 運算單元的整體布局

根據3.2節的分析，乘法電路和Xtime電路都需要8列7行的RAXN單元級聯，而以8 bit行波進位加法器為基礎的32 bit選擇進位加法器，同樣需要8列7行的RAXN單元。本文提出一種可以同時實現無符號8 bit乘法、CF(28)域乘法、32 bit選擇進位加法、最大深度為8的“與-異或-與非錐”可重構混合粒度多功能密碼運算單元(RHMCA)。如圖4為單元整體布局，基本單元命名為RAXN_U，其中橫黑線為加法的進位信號，豎黑線為輸出信號，紅線配合上級最后1 bit進位，是無符號8 bit乘法信號傳輸，P0為部分積；紅線配合黃線是CF(28)域乘法的信號傳輸，藍色線為“與-異或-與非錐”的信號傳輸。第2～6行的左4列不同于右4列，左4列每個單元多出兩個外部數據端口。

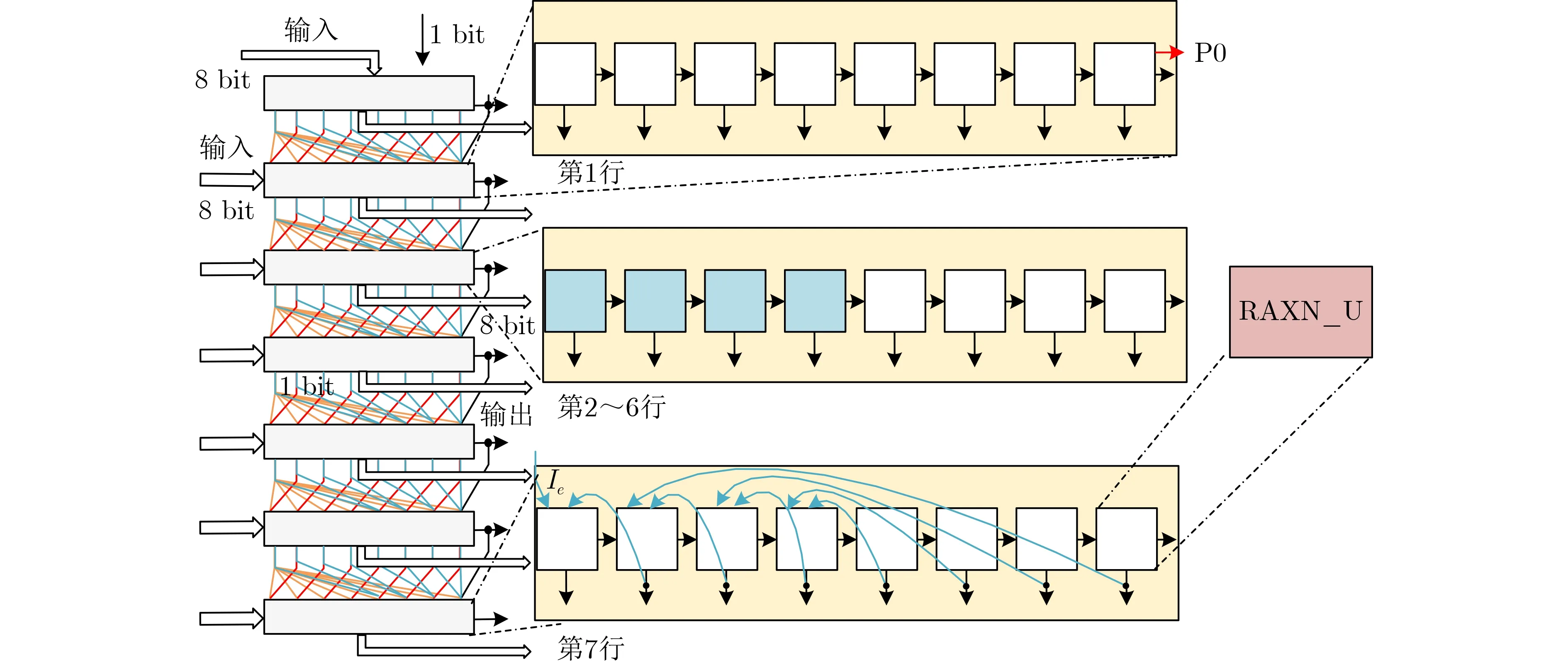
圖4 混合粒度多功能密碼運算單元

4.2 多功能實現與單元擴展

如圖5，在RAXN基礎上增加模式選擇電路、各模式下信號轉換電路。圖5(b)中F, G為模式選擇信號，ai,bi,di,di+1可為數據輸入信號，也可為配置信號，S信號為上一級輸出，C為加法進位信號。當F=1,G=0,di=0,di+1=1 ，ai,bi為數據輸入，此時執行加法，如圖5 中紅色線路；當F=1,G=1,di=0,ai為 乘數，di+1為被乘數中1 bit，同一行的di+1相同，bi為任意值，此時執行乘法運算；F=0,G=1,ai=1,di+1=1，di為不可約多項式系數，此時執行有限域乘法運算，如圖5中紫色線路；當F=0,G=0,ai=1,bi=1,di,di+1為配置信息或輸入數據，此時執行非線性布爾函數。

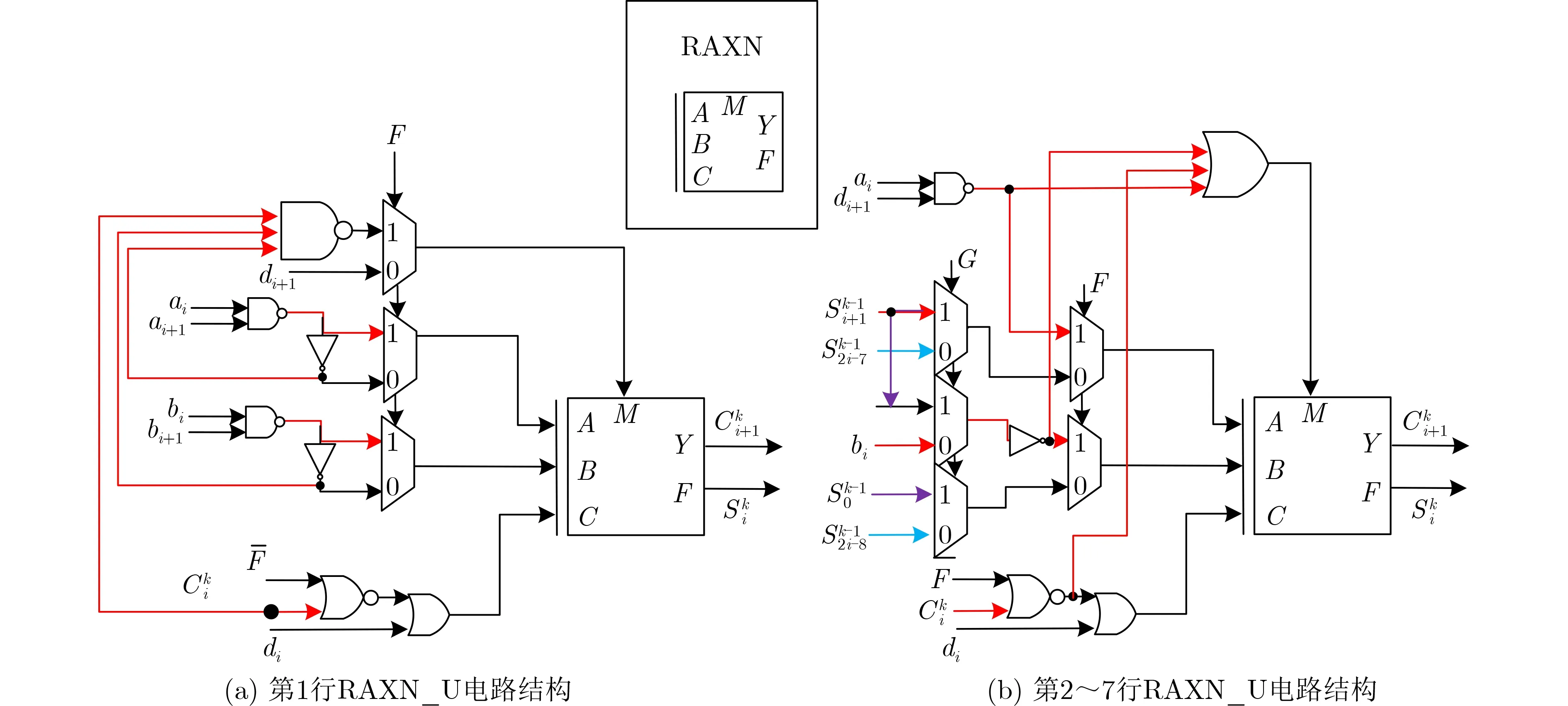
圖5 RAXN_U電路結構

本文設計單元可以直接得到7個8 bit行波進位加法器、1個無符號位的8 bit乘法、1個Xtime的功能實現。接下來重點分析復雜非線性布爾函數實現能力、擴展方式，以及高位寬擴展實現方式。

(1)靈活性。文獻[5]對CGRA在面向序列密碼時的互聯結構進行設計，利用其中的抽取電路，可以將所需的變量送入到相應位置。根據需求，送入的變量可以是反相，每個RAXN_U可以實現任意的二輸入布爾函數。除了“And,Xor,Nand,1”4種邏輯，在需要“Or”邏輯時，A,B輸入同時取反，節點邏輯配置為Nand，需要“Xnor”邏輯時，將輸入取反，節點邏輯配置為“Xor”。每一行左4個單元A,B端口不接上級輸出，可以接收外部輸入，那么本文所提出單元最高可實現72次的乘積項，或56變量的異或。第1行的輸入變量在第3行可以與第2行左4個電路輸入的變量進行運算，當第6級需要外部變量參與運算時，就可以將相關變量從第4級輸入，這樣避免了錐形結構中為實現直通功能造成的大量資源浪費。

(2)擴展能力。當1個單元無法實現復雜的函數功能，可以通過圖4中Ie的信號實現單元之間的擴展。如圖6所示，當不需要擴展時，紅色塊配置為邏輯“1”，那么每個單元可以獨立運算；但當Toyocrypt-hs1算法中的反饋函數，需要3個本文所提單元，紅色塊配置成所需的“異或”邏輯即可。相比1個單元模塊，每多擴展1個，延遲僅僅增加1個RAXN_U的延遲。

圖6 單元擴展與拆分示意圖

(3)單元拆分組合。利用外部互聯網絡中抽取電路有針對性地對所需的結果進行抽取，可以實現單元的拆分以及延遲可控及功能組合。如圖5(a)所示，第1行每個RAXN_U中可以實現2個2次乘積項，以及1個RAXN功能。因此可以利用第1行實現兩個Xtime的結果處理，則1個單元可以完成4個Xtime輸出的處理，如圖6綠色塊配置為邏輯“1”，實現了單元內部的拆分，紅線即為所需信號。在實現32 bit加法器時，第2行與第3行輸入相同的數據，但初始進位信號不同，4, 5行、6, 7行同理為一組，根據選擇進位加法器的原理，對輸出結果進行抽取。

(4)乘法位寬擴展。有限域乘法進行位寬擴展時，只有在執行LFSR并行更新功能時，需要最左邊輸出信號替換其他擴展單元的左邊第1個輸出信號，參與下一級運算，單元間每一行增加1個2:1復選器。模乘位寬只用擴展到32 bit，且整個模乘運算在密碼算法中僅有6.25%的使用率，不宜做特別改造。本文擬采用多周期實現位寬擴展。8 bit乘法結果為16 bit，區分為高8 bit (H)，低8 bit (L)，模乘運算一般只取低8 bit。在整個16 bit結果時，高8 bit的延遲約為整體延遲的1/3，因此將低8 bit全部生成的時間作為關鍵路徑延遲(時鐘周期)，可經過如圖7所示5個時鐘周期完成位寬的擴展。第1個周期，第2周期分別生成所有L,H，計算1對16 bit加得到sum0，1對24 bit加得到sum1，并輸出out0；第3個周期，計算1對16 bit加得到sum2，計算1對24 bit加得到sum3, sum3低8 bit輸出out1；第4,5個周期分別計算1對16 bit加得到sum3，1對8 bit加得到sum4，并分別輸出out2, out3。

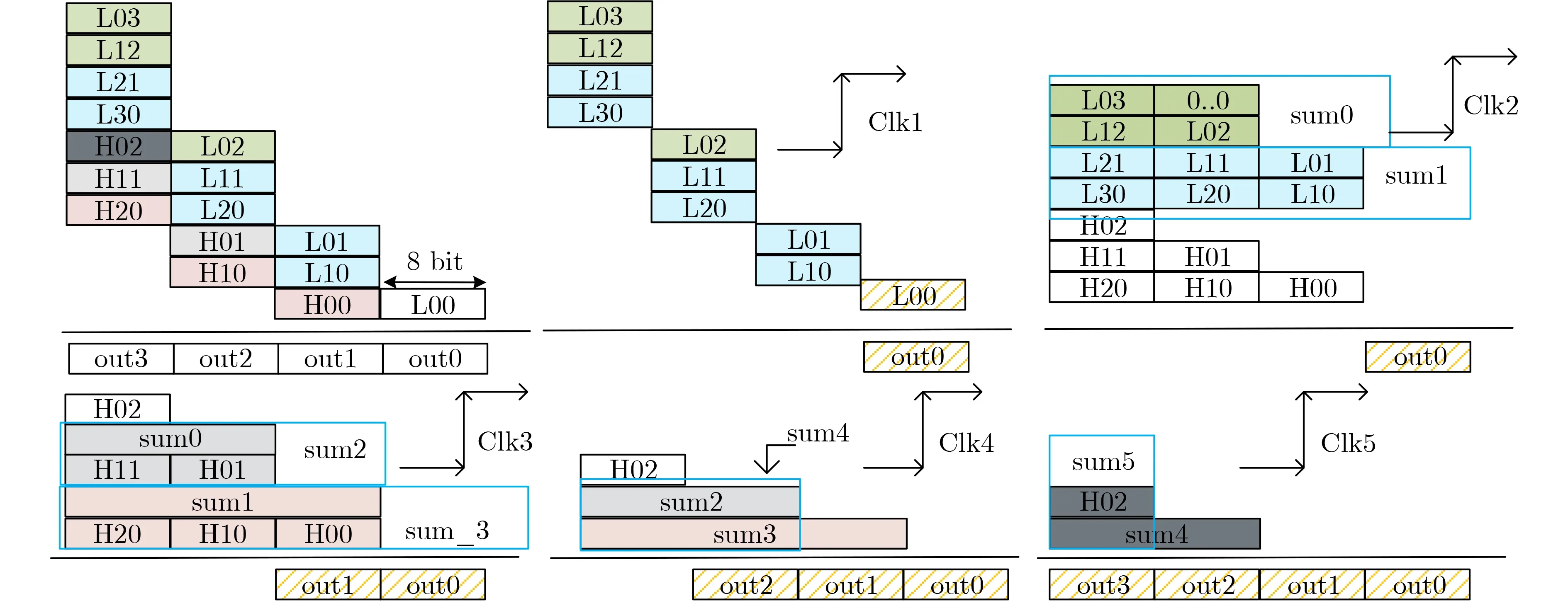
圖7 32 bit模乘計算過程

5 實驗及性能分析

在COMS 40 nm工藝，25°C, 1.1 V驅動電壓，TT工藝角環境中，為使RAXN_U信號輸出延遲最小，上升和下降沿盡量相同，調整晶體管的寬長比。對圖5(b)電路的進行版圖設計，經過布局布線和后端仿真，面積為26.9 μm2。根據連接關系，測得端口F的輸出電容為5.1 fF，端口Y的輸出電容為0.85 fF，遍歷各種功能下的輸入取值，得到如圖8各種功能模式下翻轉延遲分布。

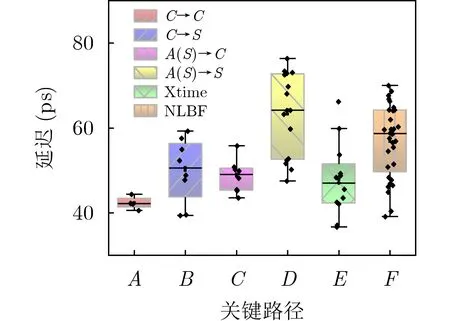
圖8 各功能模式下的延遲情況

實現加法功能時，關鍵路徑在“進位到進位(C→C)”的延遲，最大值為44.4 ps，最小值為40.6 ps；乘法陣列功能時，關鍵路徑在“加(和)位到進位(A(S)→C)”，“進位到和位(C→S)”與“進位到進位(C→C)”的延遲累加，其中“A(S)→C”的最大延遲為55.8 ps，最小值為43.5 ps，其差值為12.3 ps，“C→S”的最大延遲為59.3 ps，最小值為41.6 ps，其差值為17.7 ps。

實現Xtime功能時，關鍵路徑是上級輸出到此級輸出，最大延遲為66.2 ps，最小值為36.7 ps，差值達到30 ps，不同取值情況延遲差別過大，會導致電路中出現不必要的翻轉而增加延遲和功耗。從圖8中E可以看到延遲集中在40 ～50 ps，僅有一種翻轉延遲情況達到66.2 ps，遠大于其他值，此情況下的翻轉信號路徑最長。把冪乘中扇出為8的輸出信號-1，接入延遲信號較短的輸入端口，大扇出導致驅動能力變弱，使最小延遲增大，縮小最大延遲與最小延遲的差值，經過實驗仿真延遲差可以從30 ps降到14 ps。

實現非線性布爾函數功能時，最大延遲為70 ps，最小延遲為39.1 ps，延遲差為30.9 ps。延遲的中位數在58.7 ps，平均值在57.6 ps，說明整體延遲分布比較均勻。對于RAXN單元，從端口A,B,C進入的信號在功能函數中是等價的，因此將延遲差較為接近的兩個端口A和B作為級間傳遞信號的輸入端口，端口M和C的信號為外部輸入，延遲差可以降為15 ps。

利用EDA工具調用CMOS 40 nm工藝庫標準單元對本文所提出結構進行綜合驗證，和對本文多功能運算單元進行定制化設計后實驗仿真，如表2所示是其兩種實現方式下的不同功能延遲和總面積。

表2 兩種方式實現下延遲和面積

根據文獻[18]，對不同工藝下的延遲、面積進行歸一化處理，得到如圖9的對比結果。

圖9 不同功能模式下性能和資源占用對比

如圖9(a)是使用標準單元實現幾種專用8 bit加法器的面積、延遲以及面積延遲積(Area-Delay Product, ADP)[19]，本文所提單元實現加法功能與類似的行波進位加法器延遲降低24.6%，大約0.13 ns，相比其最快的加法器結構延遲增加40.6%，約0.11 ns；圖9(b)與傳統陣列乘法器LP，可變操作數乘法器[10]，以及定制優化的乘法器[11]的延遲進行比較，在實現8×8乘法功能時，延遲最多增加15%，約0.14 ns，與用標準單元庫實現幾種不同結構下的乘法器[20]，比較ADP值，最高得到44.8%的優化；圖9(c)為可重構NLBF運算單元比較，文獻[9]可實現幾乎所有序列密碼中以1 bit為操作位寬的NLBF，本文最多需要3個本文所提單元即可達到相同功能，在一個RHMCA基礎上延遲增加210 ps，面積增加2倍，與相關研究中最好結果RSCLU[9]比較，延遲降低1.27 ns, ADP值增加38.7%。結果表明，相比加法，乘法電路的專用電路，延遲最多增加0.14 ns，性能損失可接受；相比其他NLBF實現單元，延遲有大的提升，主要是由于AXIG在復雜布爾函數的優勢[14]；由于有限域乘法單元在對冪乘單元設計基本結構相同，若使用標準單元實現，延遲約為0.610 ns，面積為427.3 μm2，ADP為260.653 μm2·ns，本文所提單元延遲降低6.6%，約40 ps，面積增大2.54倍，ADP增加231%。綜上所述，本文由于是多功能可重構單元，與專用電路，延遲增加最大的是乘法功能時，增加0.14 ns，延遲優化最大是實現NLBF功能時，降低1.27 ns；單一功能下，實現乘法功能和NLBF功能占用面積相對較大，比較兩種功能模式下的ADP值，本文所提多功能單元在乘法功能時有0.7%～44.8%的提升，在NLBF功能時有–38.7%～82.2%的提升。

6 結束語

本文提出一種混合粒度的多功能可重構密碼運算單元，用于改善細粒度序列密碼的兼容性和避免功能單元競爭沖突。該單元利用陣列中數據抽取電路和數據分配電路，可以實現非線性布爾函數，也可以作為S盒、模乘、模加和有限域乘法的實現單元，可以有效降低電路延遲，實現密碼算子功能的可重構，系統級可重構的流水線設計和互聯網絡設計有更大的提升空間。針對本文所提單元，在算法映射、數據分配電路等方面還需要進一步研究。