面向格基后量子密碼算法的可重構多項式乘法架構

陳 韜 李慧琴 李 偉 南龍梅 杜怡然

(戰略支援部隊信息工程大學 鄭州 450000)

1 引言

量子破譯算法對RSA, EIGamal, ECC公鑰密碼產生了嚴重的威脅。Shor[1]在1994年發表了名為《Polynomial Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer》(《量子計算機上的質因數分解和離散對數的多項式時間算法》)的論文，認為在量子計算機上實現大整數因式分解僅需多項式時間，而在經典計算機上用現今最快的算法需要指數倍的時間。在此背景下，后量子公鑰密碼算法設計在網絡信息安全領域已成為新興的研究方向。

美國國家標準技術研究所(National Institute of Standards and Technology, NIST)從2012年開始啟動后量子密碼方向的研究。2018年，NIST進行了第1輪入圍算法的討論，截止到2020年10月27日，NIST公布了第3輪入圍候選者[2,3]，其中包括基于格的算法、基于編碼的算法、多變量的算法和Hash函數的簽名算法。加密算法包括Classic McEliece, CRYSTALS-Kyber, NTRU與Saber，簽名算法包括CRYSTALS-Dilithium, Falcon與Rainbow，其中CRYSTALS-Kyber, NTRU, Saber, CRYSTALS-Dilithium與Falcon都屬于基于格的密碼。2022年，第3輪標準化結果公布，屬于格基密碼的CRYSTALS-Kyber, CRYSTALS-Dilithium, Falcon確定入選。與其他幾種后量子公鑰密碼算法相比，基于格的密碼算法有以下優點：可證明安全性、公私鑰尺寸更小、計算速度更快以及在格理論密碼系統出現之前，沒有合適的問題可以用于構造同態加密系統。綜上所述，格基密碼方案被認為是最有前途的用于公鑰加密和數字簽名的后量子密碼算法。隨著格基后量子公鑰密碼的不斷發展與研究，國內也開始為量子計算機對傳統密碼算法帶來的沖擊做準備。2018年11月，由歐洲電信標準化協會主辦的第六屆量子安全國際會議在京開幕。中國科學院信息工程研究所副所長荊繼武在會上表示，中國或將于2022年左右開展后量子密碼算法標準化的工作，于2025年左右實現商業化應用落地。此表明未來常用格基公鑰密碼多樣，其中參數結構迥異需要可重構架構去實現。因此，設計一種可滿足不同算法中的多項式乘法架構具有重要意義。

針對不同參數，2019年，麻省理工學院的Banerjee等人[4]提出了一種采用Barrett取模算法可重構不同模數的多項式乘法實現方法。最終在不加流水線前提下，最大頻率可達100 MHz。2020年，來自慕尼黑工業大學的Fritzmann等人[5]將格基后量子密碼擴展到RISC-V架構上實現了3種不同的算法，其中就模數不同的架構和內存上的訪問方案進行了探究。此前大多數研究將NTT的旋轉因子進行了預計算，并將其存儲在單獨的內存中，但對于高次多項式會占用過大面積，考慮到動態計算延遲會增加，所以此設計結合預計算和動態微擾度計算的優勢，提出了一種混合使用方法。對于次數較大的多項式，例如在NewHope-512和NewHope-1 024中，使用動態計算的方式，否則使用預先計算的表，例如在Kyber算法中應用。針對不同項數和模數，2021年華中科技大學的劉冬生團隊[6]針對數論變換參數的多樣性，提出一種基于隨機存取存儲器(Random Access Memory, RAM)的可重構多通道數論變換單元。在數論變換單元設計中，按時間抽取的基礎上改進多通道架構，并提出一種優化地址分配方法。

針對不同格基后量子公鑰密碼算法，項數相同，且模數都在16 bit以內的Kyber與Saber算法經常作為可重構多項式乘法的研究對象。2020年，文獻[7]中的設計采用單路迭代的方式，迭代使用模乘單元實現Kyber, Saber與Newhope算法中的多項式乘法，此方法花費時間較長但占用較小面積。2022年，華中科技大學團隊基于此兩種算法采用Schoolbook和Toeplitz方法來實現[8]，針對每種算法進行了資源效率和性能權衡策略下可變參數和指令編程的靈活實現。此外，以同一團隊提出的Kyber與Dilithium算法為研究對象也是常見選擇[9]，針對不同模數進行模乘單元的可擴展重構設計。清華大學劉雷波團隊[10]提出的設計作為支持算法最多的硬件實現，可支持Kyber, Saber, NTRU, Dilithium, McEliece與Rainbow等6種格基后量子公鑰算法，采用陣列的形式最大限度地復用運算單元。因此，通過分析不同格基后量子公鑰密碼中多項式乘法運算特征，得到不同重構參數需求，提出統一運算網絡是目前關鍵方向之一。

針對上述分析，本文提出一種面向多種難題格基后量子公鑰密碼算法的可重構多項式乘法架構。通過分析不同參數多項式乘法的PtNTT實現算法，就其核心操作特征設計得到一個滿足實現不同基次的4×4串并行可轉換運算單元架構，并設計了其內部的可重構模乘單元。面向不同格基后量子密碼公鑰算法中的多項式乘法進行系數地址的分配需求分析，具體體現在系數地址生成邏輯、同個RAM中Bank劃分邏輯以及實際地址與虛擬地址對應邏輯。實際來看，是在前述運算單元最佳性能范圍內實現數據分配機制的優化，基于上述機制得到一種滿足基k-NTT的多Bank數據存儲結構。

2 多項式乘法運算特征分析

2.1 多項式乘法重構參數分析

面對未來對多種格基后量子密碼算法的需求，只是設計滿足一種參數或形式的多項式乘法具有局限性。本節希望采用同種形式算法，為多種參數形式的多項式乘法構造出一種可重構架構。在NIST第3輪候選標準算法范圍內，除了Falon算法需采用FFT來實現多項式乘法，其余算法都可采用NTT或變換后的算法實現。

依據不同算法中乘法的具體參數，將其總結為3種不同形式的差異——項數n、模數q以及模多項式f(x)。較多文獻針對的多項式乘法參數多為符合Kyber, Saber和Dilithium的2的冪次項數，關于NTRU中的素數項數涉及較少，通過文獻[11]的闡述，可通過擴展項數使得其實現可使用NTT算法。模數中，有滿足q=1modn素數參數的Kyber與Saber算法，也有符合Dilithium與NTRU算法的2的冪次模數，前者可采用PtNTT算法架構的實現方式達到高效的目標，同時由于模數位數差別較大，需要構造適應不同參數的模乘運算硬件結構，后者可通過擴大模數的NTT操作后直接取低位。此外，需要注意不同模多項式對于采用算法中參數的影響。

其中，ωn=1 modq，ωn/2=-1 modq。如圖1(b)所示。通過對比上述兩種不同的模多項式，可觀察到不同算法除了對應單位根不同，其運算結構具有相似性。

圖1 不同模多項式依據中國剩余定理映射示意圖

在NTRU算法中，當模多項式為(xn–1)/(x–1)=xn–1+xn–2+···+1時，可先使用NTT方法進行擴項數后的模xn–1的運算，再進行模xp–1的運算。由于xp–1+xp–2+···+1是xp–1的因式，所以可以先進行約簡高次多項式，再約簡因式低次多項式的方式。最后通過判斷比較系數得到模xp–1+xp–2+···+1的多項式。

上述重構參數分析后可總結為不同格基后量子公鑰密碼算法的多項式乘法架構特征：都可采用NTT算法的思想來實現，可采用相似的蝶形運算架構；其具體操作包括不同長度的模乘與模加減，位寬在32 bit以內；整體實現方式為多輪相同操作迭代完成，適合深度流水和高度并行操作處理。

2.2 可重構多項式乘法運算網絡分析

基于上述關于格基后量子公鑰密碼算法中多項式乘法運算特征的分析，本小節將通過整理具體算法中的運算流程，總結出可重構核心運算單元架構。可重構實現不同參數的多項式乘法時，將其分類為可直接用PtNTT算法實現、通過擴大模數間接采用PtNTT算法以及通過同時擴展模數和項數采用混合基PtNTT算法來實現。

第1種分類具體包括Kyber和Dilithium算法，項數256都為4的冪次，且模數和項數都滿足q≡1modn，不同的僅有模數大小，需通過可重構模乘單元的設計來解決不同模數位數大小的現狀。第2種分類只包括Saber算法，其模數為2的冪次，不能直接使用NTT算法來實現，可通過將模數擴展為NTT友好的數據量，且要求為最小友好數據。既保證了可采用NTT這一本身計算復雜度低的算法，又可盡量減少多余位數增加的面積消耗和時間損耗成本。最后一種分類則是以NTRU為主體的不同參數算法，其項數為素數，模數為2的冪次。此類項數已不滿足n為2的冪次這一條件，為了解決此問題，只能通過擴展項數使其可通過NTT算法來實現。在擴域過程中，由于此類算法模多項式有(xp-1)/(x-1)與xp-1，先采用NTT算法實現模xn-1， 再根據傳統模多項式的算法進行模xp-1操作。這就要求在擴域時，項數擴展必須大于原來的兩倍，且盡可能小。在選擇擴展后的項數時，需使用混合基NTT的算法，為實際減小項數帶來的面積和時間成本大幅度降低提供可行性。最終適于可重構架構的多項式乘法參數如表1所示。

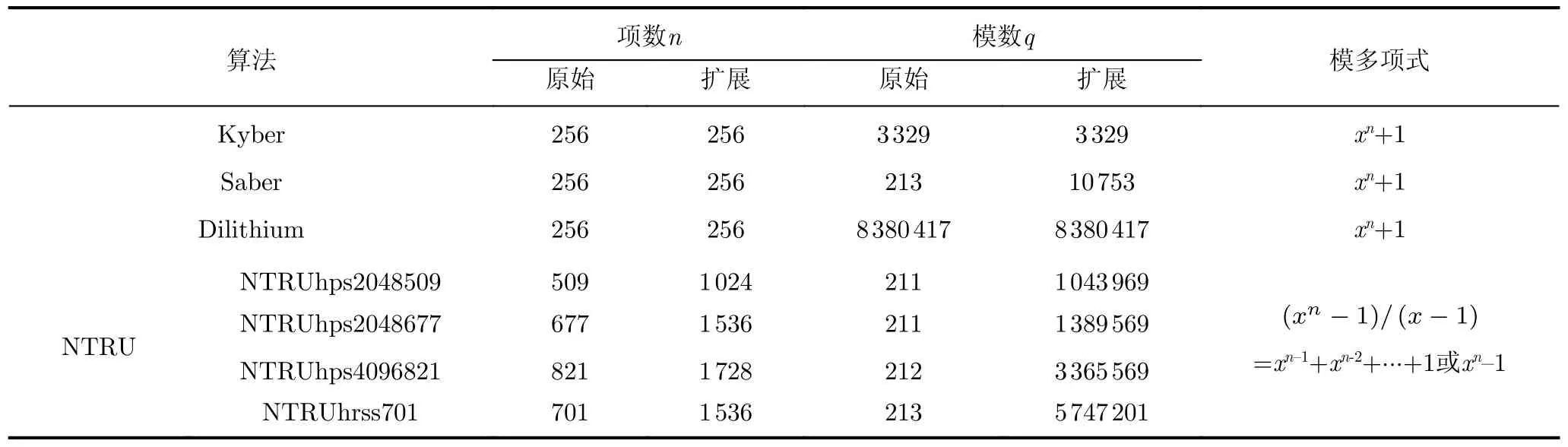
表1 適于可重構架構的多項式乘法參數

其中出現次數最多的項數為256，且為4的冪次，其余項數509, 677, 821與701可分別擴展為256×4, 512×3, 9×64×3與512×3。256, 512,9×64代表采用NTT算法的項數，其中包括2, 3與4的冪次，說明可重構架構需同時滿足基2, 基3與基4的基本運算操作；“×4”“×3”則說明需要分成3組和4組進行PtNTT算法的分組點乘計算。以NTRUhps4096821算法為例，其實際運算流程為如算法1所示。

根據上述流程需要確定可重構核心運算單元所支持的基k-NTT算法，最頻繁出現的為基4操作，且實質上是基2操作的兩層復合操作，所以需要盡可能通過并行或串行基2來實現基4；基3則是為支持盡可能減少較大項數出現的操作，其完整實現也是必不可少的。算法2—算法4詳細描述了不同基k-NTT算法的核心運算流程。

其中，i=0,1,2,...,n/3-1。

如表1所示，算法5中的T0, T1與算法6中的T2,T3進行的是相同的運算，算法5中的T2, T3與算法6中的T0, T1進行的是相同的運算，具有可重構的基礎。此外，已知需要一種架構同時實現基4、基3與基2的蝶形運算，且基4的基本操作需要4個乘法，可同時滿足4次基2的操作，基3的基本操作則是需要3個乘法，選擇基4或基2與基3重構需要明確。若選擇基2與基3蝶形運算進行重構，實現1次核心操作，基2運算會浪費1個乘法單元，基4運算會浪費2個乘法單元；若選擇基4與基3蝶形運算進行重構，僅基3運算浪費1個乘法單元。所以采用基4核心基本運算單元，在此基礎上，進行其他運算功能的增加。

則a(x)=a0(z)+x·a1(z)+x2·a2(z)， 同 理b(x)=b0(z)+x·b1(z)+x2·b2(z)。最終乘積結果多項式用c(x)表示。

算法1 NTRUhps4096821采用混合基PtNTT的多項式乘法

算法5 基4-NTT算法的核心運算操作拆解，其中μ=ωn/4

上述公式推導了3路采用PtNTT算法進行點乘運算的具體流程，4路點乘運算與之同理，下述表格中的算法具體列出了化簡后的流程。由于點乘操作是在多項式乘法中NTT與INTT之間進行的，故僅將點乘流程在下述表格中體現出來，如算法7、算法8所示。

算法7 4路PtNTT中的點乘算法

通過上述分析，不同格基后量子密碼算法中多項式乘法核心操作的實現都有共通之處，通過提煉相似操作，以最小的面積冗余實現不同參數的多項式乘法。

3 可重構多項式乘法運算架構設計

3.1 串并行可轉換型運算單元架構

依據第2節關于核心運算可重構過程的建立，需構建一個同時滿足基4、基3與基2操作的核心蝶形運算架構。根據算法5中針對基4-NTT核心運算操作拆解，具體結構如圖2所示。

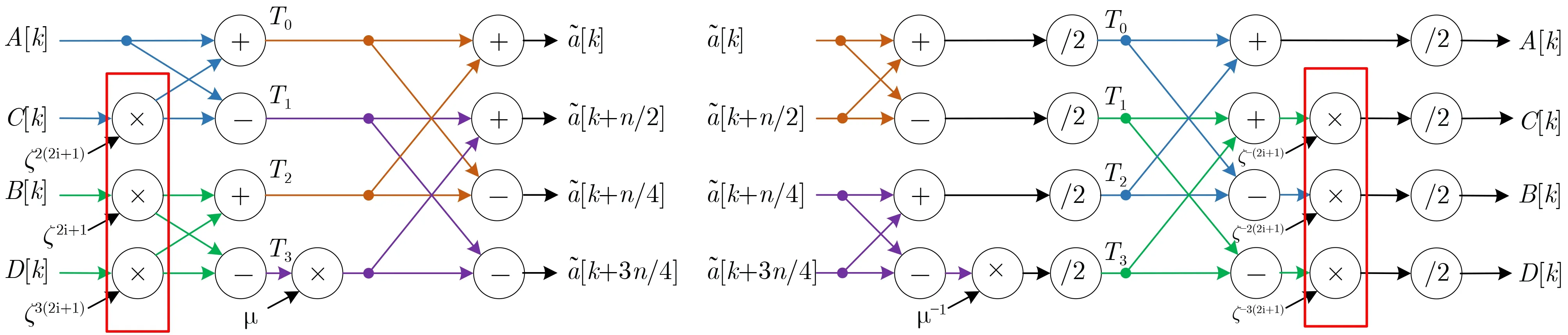
圖2 基4-NTT/INTT核心蝶形運算架構圖

若本設計以上述蝶形運算架構為基礎進行可重構單元的搭建，帶來的面積冗余過大。以紅框內的3個模乘單元為基準，前后需要各添加1個模乘單元，模加減單元數量并不會降低。觀察到其拆解運算具有高度重合性，將具有相同操作的連線用相同顏色標注出來，整體可重構運算單元與單個基4-NTT/INTT內包含的模乘單元數量相同，將操作分為4個部分，即PE0, PE1, PE2與PE3。同理，基3蝶形運算也可在4個PE內實現。

故實現基4數論變換算法結構至少為2×2、包含4種不同分操作的基本運算單元 (PE0, PE1,PE2與PE3)，其中的具體分操作是對基4與基3的可重構轉化。本設計面向算法的參數要求為0～32 bit，若僅將其中最大位寬固定到32 bit，對于小位寬的多項式乘法，將帶來3/4面積上的冗余，不滿足可重構中關于“有效利用硬件資源從而達到節約邏輯資源”的要求[12]。此擴展性設計被舍棄，故將最大位寬縮小到16 bit，滿足最小參數為3 329(12位)的要求。因此，2×2運算單元可實現1次16 bit的基4/3的核心操作。當實現16～32 bit參數的多項式乘法時，一個2×2運算單元僅能實現1次32 bit基4/3的核心操作中涉及乘法的1個步驟。考慮到對于最大工作頻率的限制，需要全流水實現。若通過復用此基本運算單元架構，浪費時間周期數較多，帶來的性能損耗較大，故設計為4×2×2(4×4)的整體運算單元架構，可完整實現1次32 bit的基4/3的核心操作。整體電路結構如圖3所示。

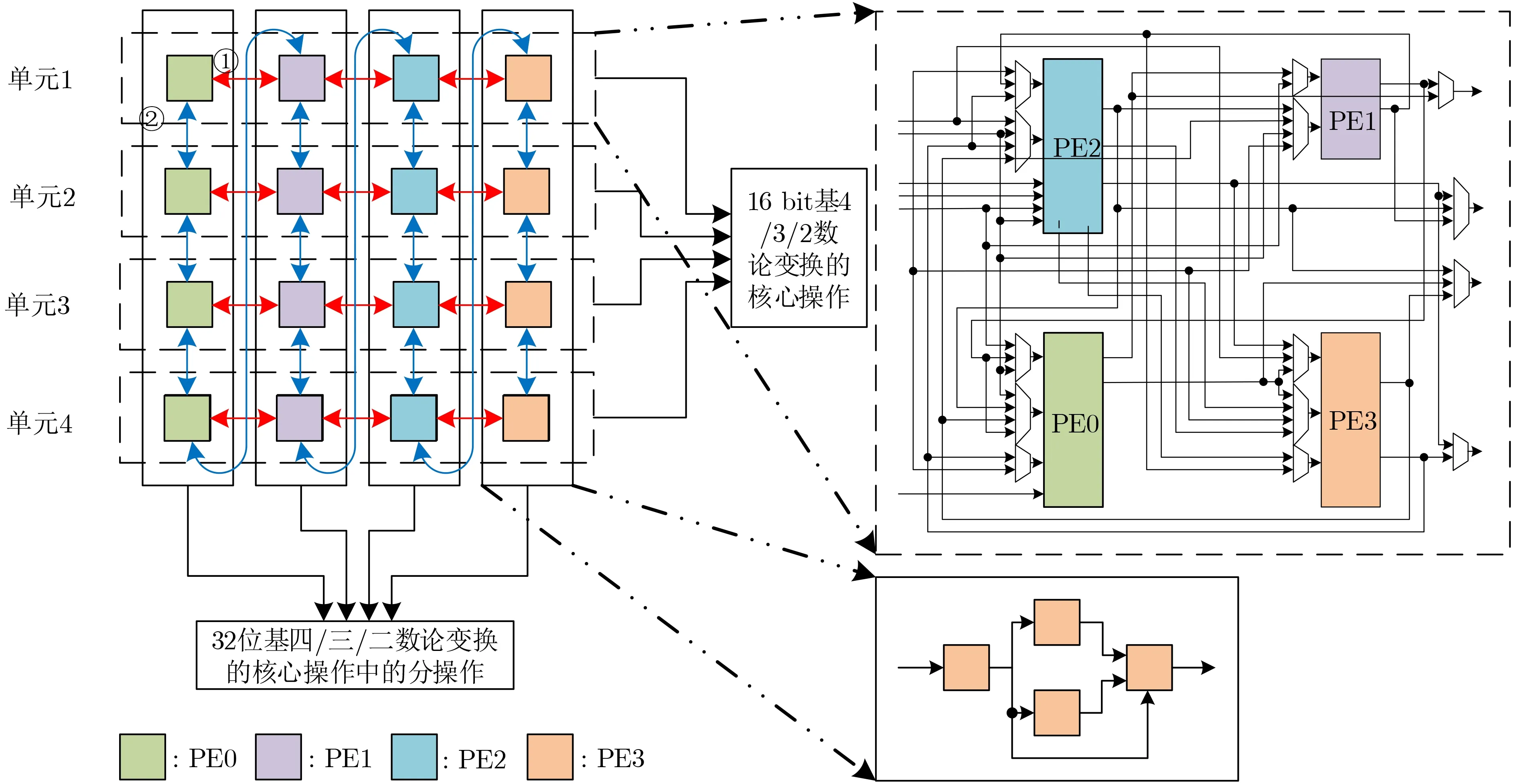
圖3 串并行可轉換型運算單元結構圖

上述結構圖對重構設計進行了描述，其中4個可重構核心運算單元(單元1—單元4)構成了整體運算架構，僅在并行計算點乘中的Ri,j時，其支持的運算略有不同。此外，在實現32 bit模乘時，各單元內的PEi共同實現圖4的功能，每個PEi完成其中的1個乘法和附加運算，實際上PEi內的單個乘法實現的是32 bit乘法(圖4單元中的選擇信號sel為0時)。

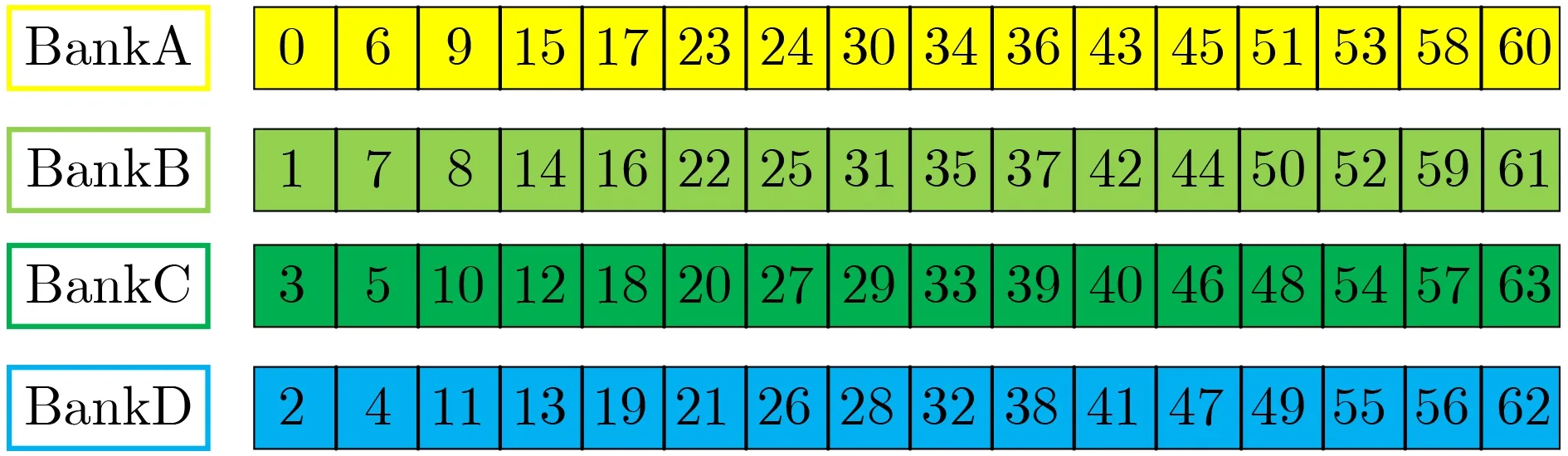
圖4 適于Kyber算法的4-Bank存儲系數情況

圖3將單元一的運算框圖進行了具體描繪，其復雜的連接和選擇關系代表可同時實現16 bit基4/3/2的NTT和INTT算法操作，紅藍箭頭代表虛線框內基于數據選擇器的互連關系。①代表單元內部PEi之間的互連，實現16 bit基4/3/2的NTT和INTT算法操作；②代表單元之間同種PE以及不同單元之間首末PEi的互連，實現32 bit基4/3/2的NTT和INTT算法操作。

3.2 可重構模乘單元設計

根據第2節針對模數的總結分析，模數支持位寬為0～16 bit與17～32 bit。直接設置大比特位寬是一種解決思路，然而相較于小比特位寬具有較大的面積冗余，且為了支持未來可能出現的其他位寬模數，本設計將通過串行16 bit的模乘來實現3 bit的模乘，同時通過運算單元的并置來實現4個16 bit的模乘。既解決了實現小比特位寬運算帶來的面積冗余，也避免了小比特位寬串行實現導致的時間成本的增加。

選擇具體模乘算法實現時，Montgomery算法與Barrett算法均具有較好的可重構功能，支持任意比特的模乘。32 bit Montgomery模乘算法具體需要3個32 bit乘法，但需要進行預處理與后處理，時間成本會成倍增加；32 bit Barrett模乘算法則具體需要4個32 bit乘法，32 bit乘法可通過4個16 bit乘法組合實現，16 bit Barrett模乘算法也可通過此4個16 bit乘法實現，如算法9所示。從而可獲得既可實現16 bit模乘又可實現32 bit乘法的可重構模乘單元結構。

4 多項式乘法存儲數據分配機制

4.1 滿足基k-NTT的數據分配機制

(1) Kyber與Saber算法

整體采取基4-2PtNTT方法來實現，即整體4×4單元其中每1×4單元實現n=64的基4 NTT操作。以裝載64個多項式系數的空間為1個RAM單元，需要同時讀寫4個數據。可得到具體的分組情況如圖4所示。

圖4所示的4-Bank存儲系數的劃分情況完全符合圖5所示Kyber算法中多項式乘法NTT/INTT要求的地址互斥關系。其次就地址生成規律與劃分規律進行討論分析。理論上需要3種計數器進行地址的生成，應將其進行精簡優化。根據算法要求，分配方案需要同一周期在一個RAM(N/4，也為下面論述中的n項)中讀出4個數據，其余3項數據可在基數據的基礎上進行改變。例如在第1子輪16項數據的基礎上加上0x010000, 0x100000與0x110000。最外部需要1個計數器Cnt0，總共運行log4n輪，內部循環Cnt1計數n/4次。內部循環每滿4log2n-1-Cnt0加上 4log2n-Cnt0，變化量實質上與Cnt0有關，所以無需新添計數器的數目。

圖5 Kyber算法中多項式乘法NTT/INTT地址互斥連通圖

故第1 子輪基數據為0 x 0 0 X X X X，其中XXXX代表Cnt1值，循環加1；第2子輪基數據為0xXX00XX；第3子輪基數據為0xXXXX00。其余3項數據在基數據基礎上，將其中00替換為01, 10和11。所以最終地址在Cnt0和Cnt1的控制下進行轉換。

整體劃分規律則是按照二進制“1”的奇偶個數進行劃分，偶數個“1”劃分為第0、第2個Bank，奇數個“1”劃分為第1、第3個Bank。然后按照a[0]^a[4], a[3]進行劃分，在第0、第2個Bank中，當a[3]為1且a[0]^a[4]為0或a[3]為0且a[0]^a[4]為1時，劃分為第2個Bank，反之分為第0個Bank。在第1、第3個Bank中，當a[3]為1且a[0]^a[4]為0或a[3]為0且a[0]^a[4]為1時，劃分為第1個Bank，反之分為第3個Bank。高log2n–2位代表其在Bank內的實際地址。Saber算法參數類型與之相同。

(2) Dilithium算法

與Kyber相似，Dilithium算法內多項式乘法項數同為256，但其模數以及適應NTT形式不同。此算法可完全按照傳統NTT算法來實現，本文為減少控制結構的復雜性，故同樣采用基4-2PtNTT算法來實現，由于模數長度為Kyber算法的兩倍，需要4×4個運算單元，每1×4個運算單元實現基4中1個階段的32 bit模乘運算，最終共同實現1次32 bit基4操作。一個裝載64個多項式系數的RAM單元，也需要同時讀寫4個數據。地址生成規律、Bank劃分規律與Kyber算法相同，只是將a[3]轉換為a[3]^a[7]。

算法9 16 bit模乘、32 bit乘法

(3) NTRUhps2048509算法

經過第2節針對NTRU算法進行NTT友好型參數轉換后，其項數為1 024，整體采用基4-2Pt-NTT方法。以裝載256個多項式系數的空間為一個RAM單元，需要同時讀寫4個數據。與前兩種分配方式相比，每個Bank內的存儲量增加，不同類算法可重構實現表明可共用存儲面積。且為了控制結構復雜度降低，分配方式需要同時滿足兩者的要求。所以前文所滿足的多種分配方式既需要滿足此算法的要求，也需要降低控制結構復雜度。

實際上，在對Kyber與Dilithium中小項數的劃分情況進行分析時，其具體分組情況具有多樣性，并不如圖4所示僅有1種劃分情況。為保證此算法中對應的大項數劃分可成功實現，減少由于地址生成邏輯復雜性的提高帶來整體單位面積性能的降低，將劃分情況更加偏向大項數劃分，在滿足此類情況的劃分前提下同時滿足Kyber, Dilithium中小項數的劃分情況，即Bank劃分規律上述算法是相一致的。

地址生成規律實質上也與第(1)節陳述類似，本質在于項數不同帶來的計數范圍的不同。Cnt0,Cnt1分別與log4n, n/4有關。其地址生成規律變為了第1 子輪基數據為0 x 0 0 X X X X X X，其中XXXXXX代表Cnt1值，循環加1；第2子輪基數據為0xXX00XXXX；第3子輪基數據為0xXXXX00XX；第4子輪基數據為0xXXXXXX00。其余3項數據在基數據基礎上，將其中00替換為01, 10和11。

(4) NTRUhps2048677與NTRUhrss701算法

第2節針對NTRU算法進行NTT友好型參數轉換后，其項數都為1 536(512×3)，整體采用基2數論變換與3路預處理相結合的方法。以裝載512個多項式系數的空間為一個RAM單元。作為分組數據較大的算法，且針對32 bit基2蝶形操作的4路并行實現方案，需要同時讀寫4個數據。

其地址生成規律與基二蝶形操作相關，與上述基4操作具有相通之處。Cnt0, Cnt1分別與log2n,n/2有關。其地址生成規律變為第1子輪基數據為0 x 0 X X X X X X X X，其中X X X X X X X X 代表Cnt1值，循環加1；第2子輪基數據為0xX0XXXXXXX；依此類推，最后1子輪基數據為0xXXXXXXXX0。其余一項數據在基數據基礎上，將其中0替換為1。

(5) NTRUhps4096821算法

作為NTT友好型參數轉換后項數最大的多項式乘法，其項數為1 728(9×64×3)，整體采用混合基數論變換與3路預處理相結合的方法。需要先進行基3數論變換運算，再進行基4數論變換運算，然后進行點乘，最后進行逆數論變換運算。

由于是混合基次數論變換，其地址生成邏輯與上述論述出入較大，同樣保證以簡單的布爾邏輯與循環計數來實現。基3數論變換以64為數量單位的地址塊為整體進行地址轉換，則簡化為n=9的蝶形操作，擴展到64×9可直接通過移位實現；基4數論變換則以9為數量單位的地址塊為整體進行地址轉換，與上述基4數論變換地址生成規律吻合，即與第(1)節論述完全相同。

在對Bank劃分規律進行分析前，需要注意的是，在混合基次過程中基數變換的這一階段，由于存在讀出的數據經過運算不再寫回到原來的地址上這一問題。若以增加存儲面積作為代價，多出1倍的存儲區，分別用來存儲3-Bank與4-Bank的數據。本身作為最大項數的多項式乘法，其存儲面積占用較大，使得其他算法的實際有效占用率較低。此問題主要出現在基3與基4混合基操作時，同一系數在不同分配操作中占據不同的Bank與實際內存地址。所以解決思路為不額外占用存儲面積的前提下完成虛擬地址與實際地址的相統一。

為使地址相統一，將RAM劃分為3與4的最小公倍數——12個Bank。同時以兩種劃分規律為抓手，分為0.BankA、1.BankB、···、2.BankC與2.BankD。但實際上，若是均勻分配(按照63×11+70)，最終并不能正確匹配實際運算過程中的地址，會出現讀寫數據有可能會存在于同一Bank中從而產生讀寫數據沖突。需通過整塊地址的調整最終得到可同時滿足基3與基4的多Bank數據存儲方案。

以適應基3的存儲量9的存儲單元為整體，稱為存儲塊。存儲塊內的系數地址是連續變化的，則存儲塊的塊號是以適應基4的存儲量64進行計數，可劃分為4個Bank；當以適應基4的存儲量64的存儲單元為整體，稱為存儲條。存儲條內的系數地址是連續變化的，則存儲塊的塊號是以適應基3的存儲量9進行計數，可劃分為3個Bank。最后綜合來看可分為12個Bank。為方便實際地址到內存地址的轉換，以存儲塊的形式進行保存。最終具體12Bank地址劃分如圖6所示。

圖6 12-Bank地址劃分標識圖

設計在應用于多種算法中的多項式乘法時，此RAM存儲方式中1 Bank中存儲數據量最大為54，第(1)(2)(3)節中每個Bank最大存儲量為64，與之相近，無需修正。但只占用4個Bank，在控制邏輯中，可將其余無用Bank不添加進可選擇范圍內。第(4)節中每個Bank最大存儲量為128，為最大限度增大存儲面積的有效占用率，可將此類算法存儲模式分為8個Bank，將每個Bank存儲量降為64，前提需將此Bank劃分滿足其地址的讀寫互斥關系。

4.2 滿足基k-NTT的存儲單元設計

數據分配機制確定后，需要根據具體算法的實際需求設計出具有精簡式控制結構的存儲單元，控制完成多項式系數的調度，計數使能信號的產生和轉換以及其他關鍵控制信號的產生。

在此基礎上精簡存儲單元的復雜度，并行度為16，RAM分組組數為12，每一輪運算地址的轉換需要計數器進行輔助設計。以最簡單的基4蝶形操作為例，l og4(n/4)輪運算之間需要1個計數器Cnt0進行輪數k的更新；每一輪運算內部需要1個計數器Cnt1進行4k次系數的調度；具體進行系數調度時，計數器Cnt2進制/與第1個輪數計數值Cnt0有關，每當加到(n/16)4k重新以全新的數字進行計數。若按照此設計方法至少需要3個計數器，最終4個讀地址由3個計數器的值加減組合得到。針對這一問題，需要通過布爾函數，移位等簡單邏輯運算將地址轉換進行優化，從而減少計數器的數目。

將計數器Cnt1(Cnt_Addr)進數值設置為基本的n/4，實際系數是在此基礎上通過移位或其他簡單運算產生；計數器Cnt0(Cnt_RAM)將Cnt1的進位信號作為計數使能信號；Cnt2則是計數器Cnt0值和Cnt1值共同決定，不需要再設置冗余的計數器。最終讀寫地址則是由計數器Cnt1值硬連線形成，根據Cnt_RAM值的不同，在讀數時，決定在不同的位置插入“00”, “01”, “10”或“11”。A ddr={2′bZ0,Cnt_Addr[log2n/4-1,0]}，填充的數據取決于不同的Bank選擇，填充位置則是由實現NTT的輪數Cnt0有關。根據地址漢明重量的奇偶性以及其中3位的不同將其分為4組。對于不同Bank地址的選擇生成邏輯具體為

對于單個Bank的地址生成邏輯Addr_Bank_wt=Addr_wt>>2， Addr_Bank_rd=Addr_rd>>2。對于圖7中的sel_x信號對應上述地址選擇生成公式括號內的判斷條件。

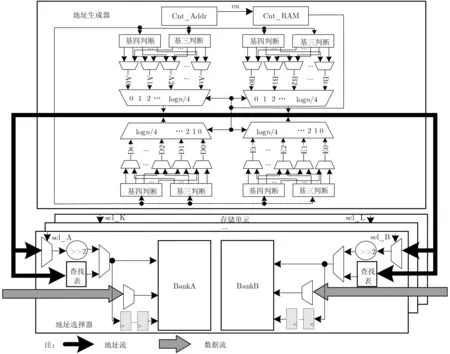
圖7 多端口RAM單元硬件設計框圖

若是較為復雜的混合基運算，由于在不同的基k蝶形操作中，存儲塊內的數據量是不同的。整體以塊號為地址生成邏輯的基礎，之前基地址的簡化生成方式實際上利用了二進制表示的優勢，所以基3操作中基地址的形成以及其余地址的衍生不能伴隨簡單的硬連線完成。只能通過算法中簡單的乘加實現，×3通過移位和加來實現，×9則是迭代實現兩次×3。其次針對混合基多Bank的劃分規律進行分析，實際上是基于數據量為9存儲塊的塊號進行劃分，則是先根據基3的Bank劃分規律——當(a[0]+a[1])mod3=0，劃分到第0個Bank；當(a[0]+a[1])mod3=1，劃分到第1個Bank；當(a[0]+a[1])mod3=2，劃分到第2個Bank。再根據上述基4蝶形操作中Bank劃分規律得到12Bank的具體劃分形式。最后將問題聚焦到系數對應虛擬地址至Bank內實際地址的轉換，混合基中多Bank中不再是上述可以直接通過簡單移位來實現地址轉換。且為了更容易兼容未來不同種情況的混合基地址轉換情況，設置4個查找表，將虛擬地址與實際地址進行對應，即4個6×576 bit大小的ROM存儲其對應關系。最終基于PtNTT算法中其中一個分組對應的存儲單元及對應控制結構如圖7所示。

存儲單元進行Bank分配不沖突的優化，實現了在不同的運算階段，讀出和輸入地址不沖突且Bank數量最小，從而保證了地址分配最優的多端口RAM設計。

5 結果與比較

本文通過Vivado 2 019.1軟件進行仿真綜合，芯片型號為Artix-7中的xc7a35tfgg484-3，最高工作頻率可達到152 MHz，共占用13 794個LUT硬件資源。

通過查閱并列舉近幾年相關文獻，發現與NTRU算法中的多項式乘法可重構架構相對較少，Kyber算法則是作為較易重構的架構，由于與Saber算法中項數相同易于重構，與Dilithium則是同一團隊研發，可采用相同的NTT算法架構。本文則是將上述4種格基后量子密碼算法中的多項式乘法進行重構。

從可重構功能和具體實現方式來說，文獻[7]中的設計支持NewHope, Kyber和Saber中16 bit以內的多項式乘法，且為低并行度實現，占用面積小但花費周期數較多。文獻[8]雖然同時支持Kyber, Saber中的多項式乘法，然而分別采用Schoolbook和Toeplitz方法來實現，實際上使用兩種不同的乘法器，并不是可復用的，起碼會占用36個Toeplitz乘法器與支持Kyber算法中NTT實現方法的模乘單元。

文獻[9]、文獻[10]都是支持Kyber與Dilithium中多項式乘法的重構。文獻[9]中兩種參數的花費時鐘周期數相同，說明其關鍵路徑限制在32 bit相乘，再加上32路蝶形運算單元，優點是時鐘周期數較少，但單位面積性能不高。文獻[10]支持算法眾多，主要分為兩類—采用NTT方法實現的Kyber與Dilithium算法，采用分層Karatsuba方法的Saber,NTRU算法，在25 nm工藝下工作頻率高達500 MHz。雖然其占用面積較大，然而實現功能較多，可支持基于不同難題算法對應的多項式乘法。文獻[13]中則是將Dilithium與Saber算法中的多項式乘法同時采用NTT架構來實現的，通過改變擴大Saber算法中的模數共用蝶形單元架構，與本文設計思想相近。要說明的是，文獻[10]與文獻[13]是基于ASIC條件下完成，故未在表2中體現。

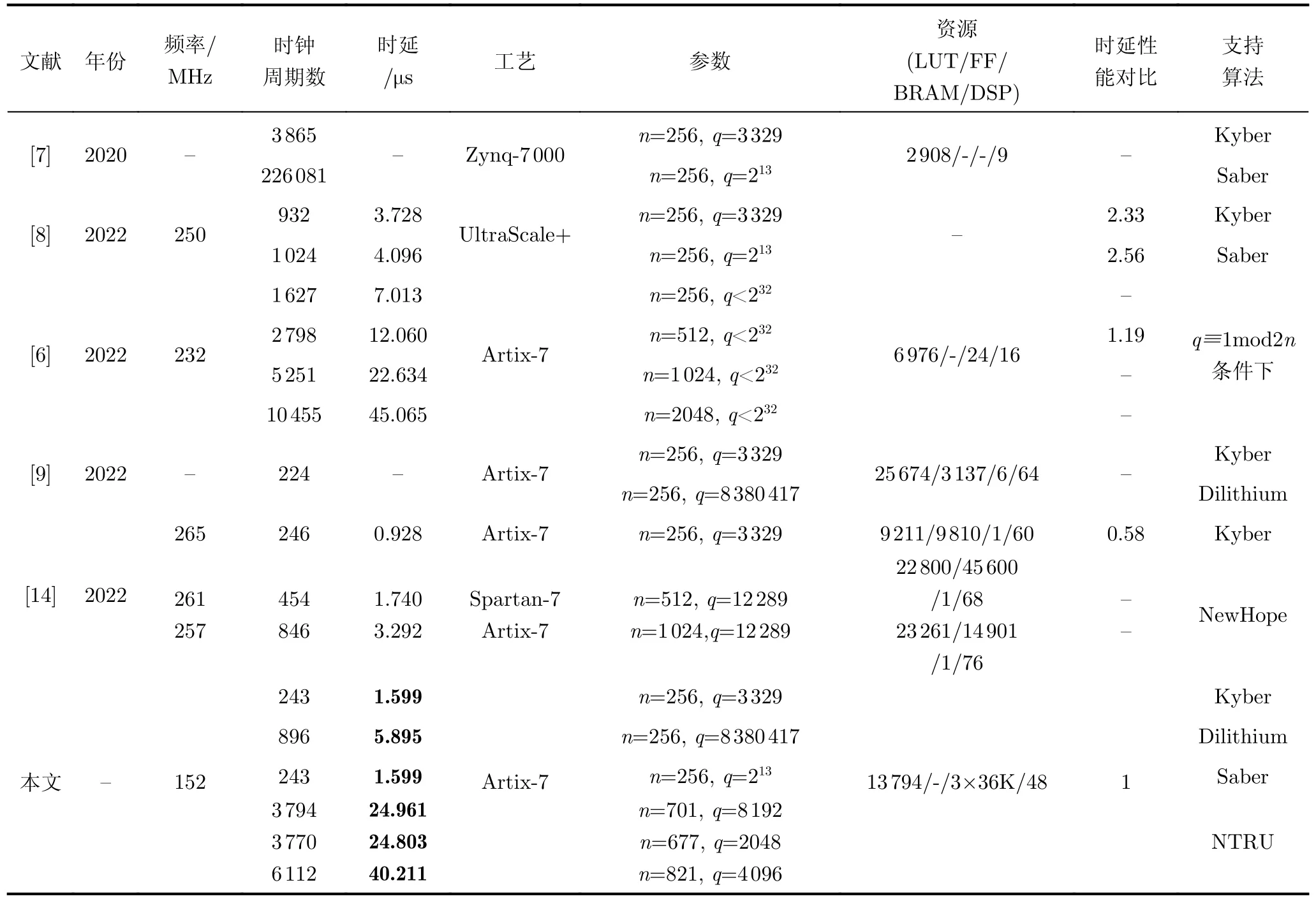
表2 基于FPGA不同多項式乘法架構性能對比

文獻[14]提出了一種高效的混合基數MDF NTT架構，適用于高性能大規模數據密碼處理器。靈活的設計使NTT架構適應各種參數集并且基數值的合理選擇有助于實現高性能。其支持Kyber以及與之參數要求相同的NewHope算法(現已落選)，靈活性范圍有限。文獻[6]則提出一種基于隨機存取存儲器(Random Access Memory, RAM)的可重構多通道數論變換單元支持實現項數256～2048，模數在32 bit范圍內。靈活性強的關鍵在于設計了基于RAM的可重構模乘單元，針對特定參數(滿足q≡1mod2n條件)優化的模乘器在資源消耗方面具有明顯的優勢，但不適用于多參數可重構設計。

通過上述分析，本文設計了實現Kyber, Saber,Dilithium和NTRU等4類算法中多項式乘法的可重構架構。在面向未來可能出現的格基后量子公鑰算法的形勢下，本文提出的架構具有高靈活性的優勢。經對比可得，采用PtNTT算法的多項式乘法單元架構其時延性能較多優于其他文獻中的數據。這是由于選用算法本身帶來的時間復雜度低，4×4并行結構和統一化運算單元保證在性能上的提升。

整體來看，本文所提基于PtNTT算法可重構多項式乘法架構，支持4種格基后量子公鑰密碼，為未來針對可重構目標的多項式乘法提供架構設計建議。

6 結束語

本文通過論述針對多項式重構參數的分析，為后續可重構網絡的建立提供理論基礎。具體來看，通過分析不同參數多項式乘法的PtNTT實現算法，就其核心操作特征設計得到一個滿足實現不同基次的4×4串并行可轉換運算單元架構，并設計了其內部的可重構模乘單元。面向不同格基后量子密碼公鑰算法中的多項式乘法進行系數地址的分配需求分析，具體體現在系數地址生成邏輯、同個RAM中Bank劃分邏輯以及實際地址與虛擬地址對應邏輯，基于上述機制得到一種滿足基k-NTT的多Bank數據存儲結構。為可重構多項式乘法提供架構設計建議。