壓力作用下KNbO3相變行為的分子動力學研究

張旭龍 曹玉瑩 周 龍 馬 治

（寧夏大學物理學院，寧夏 銀川 750021）

0 引言

鐵電材料由于具有優異的介電性、壓電性、熱釋電性、鐵電性且具有光電效應與聲光效應，受到了廣泛關注，并在鐵電存儲器、紅外探測器及光學傳感器等方面具有十分重要的應用。近年來，由于鐵電材料存在極化強度與溫度和電場的有效耦合，發現鐵電材料在相變溫度附近具有很大的電卡效應，鐵電材料被認為是下一代固態制冷器件的理想選擇。為了發展對環境友好且更加廉價高效的冷卻技術，大量的電卡制冷器件應用研究已經被報道［1-2］。由于極化強度與應變梯度之間的耦合作用，發現鐵電材料具有優良的撓曲電效應，并被廣泛地應用于撓曲電能量采集器、撓曲電致動器、撓曲電傳感器等電子器件上［3-5］。

鐵電材料具有的一個重要特征就是相變點。在溫度誘發極化相變中，將鐵電相向順電相轉變的相變點也稱為居里點。在居里點以下，材料為鐵電體，展現出優異的鐵電性，在居里點以上，材料為順電體，不具有鐵電性，極化強度為零。同時，由于鐵電體的許多物理性質，如比熱容［6］、極化強度［7］、介電常數［8］等，其在居里點附近會發生突變，在居里溫度點所測量的值較大，偏離在其他溫度下測量到的值。近年來，研究人員通過試驗測量與理論計算積極探索鐵電材料在高溫或者高壓下物理性質發生改變的規律，深入研究了許多鐵電材料在溫度或者壓力作用下的相變行為。在鐵電材料中，鈣鈦礦型鐵電體是研究范圍最廣、研究熱度最高的一類鐵電材料，研究表明在高溫或者高壓下，鈣鈦礦型鐵電體的對稱性升高，結構變得更加規則，引起鐵電體的自發極化減小，導致鐵電性能降低，鐵電材料最終變為順電材料。

KNbO3作為典型的鈣鈦礦型鐵電體，其在溫度作用下的相變行為受到了廣泛關注。Sepliarsky等［7］使用分子動力學模擬研究表明，其相變溫度依次為225 K、475 K 和675 K。Hashimoto 等［8］使用分子動力學模擬研究表明其相變溫度依次為325 K、525 K 和700 K。Golovina 等［9］通過試驗研究表明其相變溫度依次為263 K、498 K 和708 K。關于KNbO3在壓力作用下的相變行為研究較少。另外，試驗基本都是通過分析晶格參數來獲得KNbO3的相變壓力，很少通過分析其極化性能來獲得相變壓力。因此，本研究使用分子動力學方法對KNbO3鐵電體在壓力作用下的相變行為開展研究，通過分析鐵電材料極化強度與晶格參數隨壓力的演變行為獲得KNbO3鐵電體的相變壓力。同時，還研究了相變壓力的尺寸效應和電場對相變壓力的影響，這為鐵電材料相變壓力的調控起著較好的指導作用。

1 研究方法

分子動力學模擬被認為是研究許多離子系統結構和特性的有力工具，已經被廣泛用來開展材料性能的研究。本研究基于Mitchell 和Fincham 提出的絕熱核殼模型［10］，使用LAMMPS 軟件包對KNbO3開展分子動力學研究。在分子動力學研究中，絕熱核殼模型不僅可以考慮離子極化，也可以考慮電子極化，所以它被廣泛用于模擬BaTiO3、SrTiO3、PbTiO3、KNbO3、LiNbO3、KTaO3、Bi4Ti3O12等一系列鈣鈦礦型鐵電材料。在核殼模型中，每一個原子都由一個帶正電的核和一個帶負電的殼組成，核和殼都帶有部分電荷，核與殼的電荷之和就是每個原子的總離子電荷，核和殼的位置是以完全動態的方式確定的，其中核的質量占單個原子質量的90%，殼的質量占單個原子質量的10%［11］。

在KNbO3鐵電體的模擬過程中，使用的相互作用勢參數取自Sepliarsky 和Phillpot 等人開發的勢函數［7］，該勢函數主要由兩部分組成。第一部分是不同原子的殼與殼之間的相互作用，是通過Buckingham勢描述的，見式（1）。

式中：r表示兩個不同原子之間的距離；A、ρ和C是勢函數的參數。第二部分是同一原子的核與殼之間的相互作用，是通過core-shell 勢來描述的，見式（2）。

式中：r表示同一原子核殼之間的距離；k2和k4是勢函數的參數。KNbO3鐵電體使用的勢函數見表1。

表1 KNbO3鐵電體的勢函數參數[12]

2 結果與分析

2.1 壓力作用下的相變行為研究

為了研究KNbO3在壓力作用下的相變行為，模擬中使用了三斜相（R3m）結構，構建了尺寸為10×10×10 的超胞（4.09 nm×4.09 nm×4.09 nm），總原子數為10 000。模擬設定時間步長為0.4 fs，使用周期性邊界條件，在溫度為250 K 的條件下，600 000步內將壓力從0.000 1 GPa 升高到10 GPa。研究了KNbO3在三個方向上的極化強度及晶格參數隨壓力的演變行為，研究結果如圖1所示。

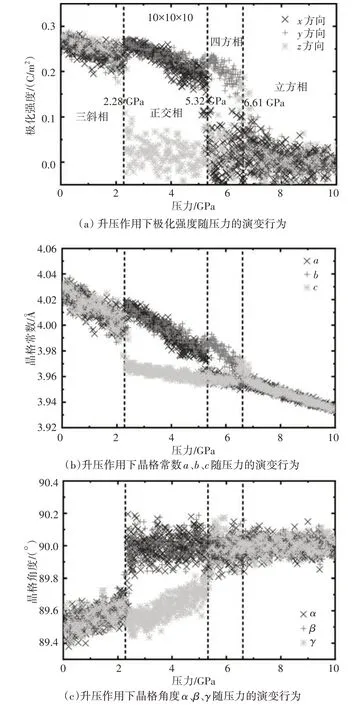
圖1 升壓作用下KNbO3的相變行為

如圖1（a）所示，在壓力作用下，KNbO3依次經歷了鐵電三斜相（R）→鐵電正交相（O）→鐵電四方相（T）→順電立方相（C）的相變過程。在低壓條件下，極化強度Px=Py=Pz≈0.28 C∕m2，KNbO3展現出的是鐵電三斜相（R）。當壓力升高到2.28 GPa 時，極化強度Px=Py≈0.28 C∕m2，Pz≈0 C∕m2，KNbO3表現出鐵電三斜相（R）向鐵電正交相（O）轉變的相變行為。當壓力升高到5.32 GPa 時，極化強度Py≈0.28 C∕m2，Px=Pz≈0 C∕m2，KNbO3表現出鐵電正交相（O）向鐵電四方相（T）轉變的相變行為。當壓力升高到6.61 GPa時，Px=Py=Pz≈0 C∕m2，KNbO3表現出鐵電四方相（T）向順電立方相（C）轉變的相變行為。KNbO3鐵電三斜相（R）的晶格常數a、b、c分別為4.09 ?、4.09 ?、4.09 ?，晶格角度α、β、γ分別為89.797°、89.797°、89.797°，順電立方相（T）的晶格常數a、b、c分別為4.057 ?、4.057 ?、4.057 ?，晶格角度α、β、γ分別為90°、90°、90°。晶格常數a、b、c和晶格角度α、β、γ隨壓力的演變行為如圖1（b）和圖1（c）所示，研究表明在壓力為0.000 1 GPa時，晶格常數和晶格角度的模擬結果與對應結構的參數比較吻合，在KNbO3晶格常數和晶格角度隨壓力的演變行為中仍然可以獲得KNbO3的相變壓力，依次為2.28 GPa、5.32 GPa和6.61 GPa。

另外，研究了KNbO3在壓力作用下發生相變行為展現出的滯后現象。仍然使用上述研究中構建的模型，模擬條件保持不變，在600 000步內將壓力從10 GPa降低到0.000 1 GPa，KNbO3在三個方向上的極化強度隨壓力的演變行為如圖2所示。

圖2 降壓作用下KNbO3的相變行為

如圖2所示，研究發現在降壓作用下，KNbO3依次經歷了順電立方相（C）→鐵電四方相（T）→鐵電正交相（O）的相變過程，其相變壓力依次為6.19 GPa、4.98 GPa，相較于升壓作用下獲得的相變壓力6.61 GPa、5.32 GPa 和2.28 GPa，在壓力作用下相變行為仍然表現出滯后現象。其中將4.98～5.32 GPa 之間的區域稱為鐵電正交相（O）和鐵電四方相（T）的兩相共存區，將6.19～6.61 GPa 之間的區域稱為鐵電四方相（T）和順電立方相（C）的兩相共存區。

其他研究人員通過試驗測量獲得的相變壓力見表2，將本研究模擬獲得的相變壓力與其他研究人員的試驗結果進行比較。Shen 等［13］通過拉曼散射測量得出KNbO3的三個相變壓力依次為2 GPa、6 GPa 和9 GPa。Chervin 等［14］在溫度為300 K 的條件下研究了KNbO3的相變行為，研究表明KNbO3從鐵電正交相（O）到鐵電四方相（T）的相變行為發生在4～5 GPa，鐵電四方相（T）到順電立方相（C）的相變行為發生在9 GPa。Shamim 和Ishidate［15］通過拉曼散射研究了KNbO3的相變行為，表明KNbO3從鐵電正交相（O）到鐵電四方相（T）及進一步到順電立方相（C）的相變行為依次發生在7 GPa、8 GPa。KNbO3相變壓力的模擬結果與其他研究人員的試驗結果之間存在一定的差異，產生這些差異的原因可能主要是測量條件及模擬過程中一些參數的設置不同，如溫度、升壓速率等。另外，尺寸效應也是影響相變壓力的一個主要因素［16-17］。

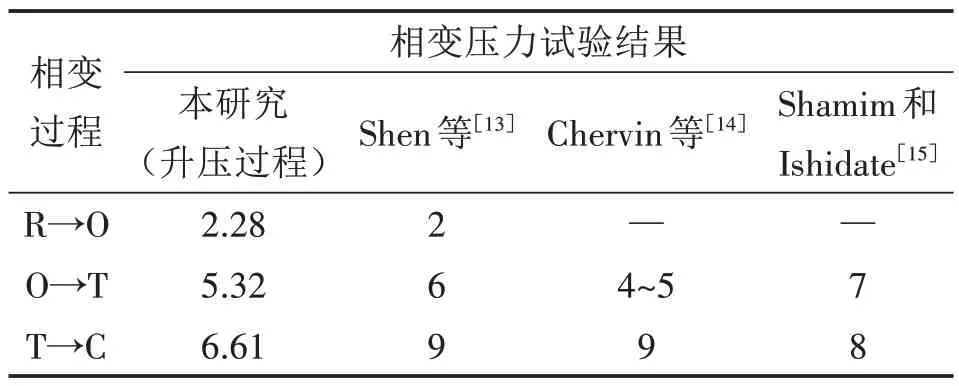
表2 KNbO3相變壓力比較單位：GPa

2.2 相變壓力的尺寸效應

為了進一步分析樣品尺寸大小對KNbO3相變壓力的影響，在模擬中仍然使用了三斜相（R3m）結構，構建了尺寸依次為8×8×8（3.272 nm×3.272 nm×3.272 nm）、10×10×10（4.09 nm×4.09 nm×4.09 nm）、12×12×12（4.908 nm×4.908 nm×4.908 nm）、14×14×14（5.726 nm×5.726 nm×5.726 nm）、16×16×16（6.544 nm×6.544 nm×6.544 nm）和18×18×18（7.362 nm × 7.362 nm × 7.362 nm）的超胞，總原子數依次為5 120、10 000、17 280、27 440、40 960 和58 320，分別研究了不同模型在壓力作用下的相變行為。模擬中仍然設定時間步長為0.4 fs，使用周期性邊界條件，溫度為250 K 的條件下，在600 000 步內將壓力從0.000 1 GPa 升高到10 GPa。所有尺寸下樣品的研究結果如圖3所示。

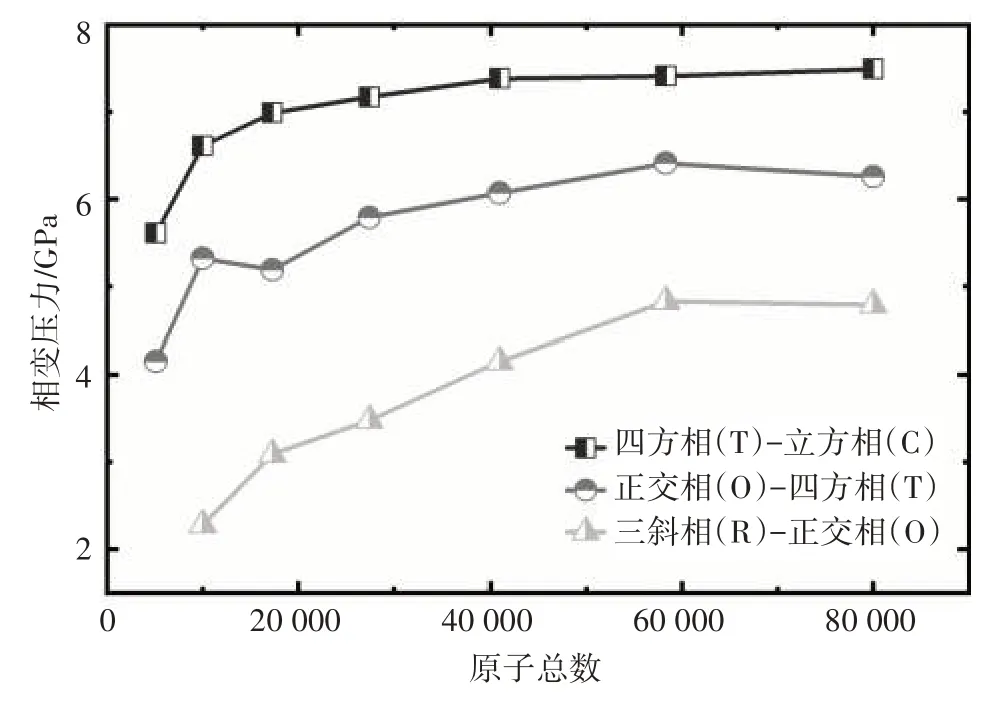
圖3 相變壓力的尺寸效應

不同尺寸KNbO3的相變壓力點如圖3 所示，研究表明KNbO3的相變壓力具有非常顯著的尺寸效應。當體系的原子總數小于30 000時，三個相變壓力點隨著原子數目的增多變化很大；當體系的原子總數超過30 000 時，鐵電正交相（O）向鐵電四方相（T）和鐵電四方相（T）向順電立方相（C）轉變的相變壓力保持穩定；而只有當體系的原子總數超過60 000 時，鐵電三斜相（R）向鐵電正交相（O）轉變的相變壓力才會保持穩定。因此，只有當KNbO3體系的原子總數超過60 000時，才能獲得穩定的相變壓力。另外，研究表明，當KNbO3的原子總數大于10 000 時，從鐵電三斜相（R）到鐵電正交相（O）的相變壓力在2.28～4.83 GPa之間，從鐵電正交相（O）到鐵電四方相（T）的相變壓力在5.32～6.41 GPa 之間，這與Shen等［13］的試驗結果比較接近。從鐵電四方相（T）到順電立方相（C）的相變壓力在6.61～7.41 GPa之間，這與Shamim 和Ishidate［15］的試驗結果比較接近。

2.3 電場對相變壓力的影響

進一步研究了電場的大小和方向對相變壓力的影響，在模擬中仍然使用了三斜相（R3m）結構，構建了尺寸為10×10×10（4.09 nm×4.09 nm×4.09 nm）的超胞，總原子數為10 000。模擬中設定時間步長為0.4 fs，使用周期性邊界條件，在溫度為250 K 的條件下，在600 000 步內將壓力從0.000 1 GPa 升高到10 GPa。同時分別在［001］、［110］和［111］方向上施加恒定電場，對應的電場分別設置為［0，0，E］、［E，E，0］和［E，E，E］的形式，研究了電場大小和方向對相變壓力的影響，研究結果如圖4所示。

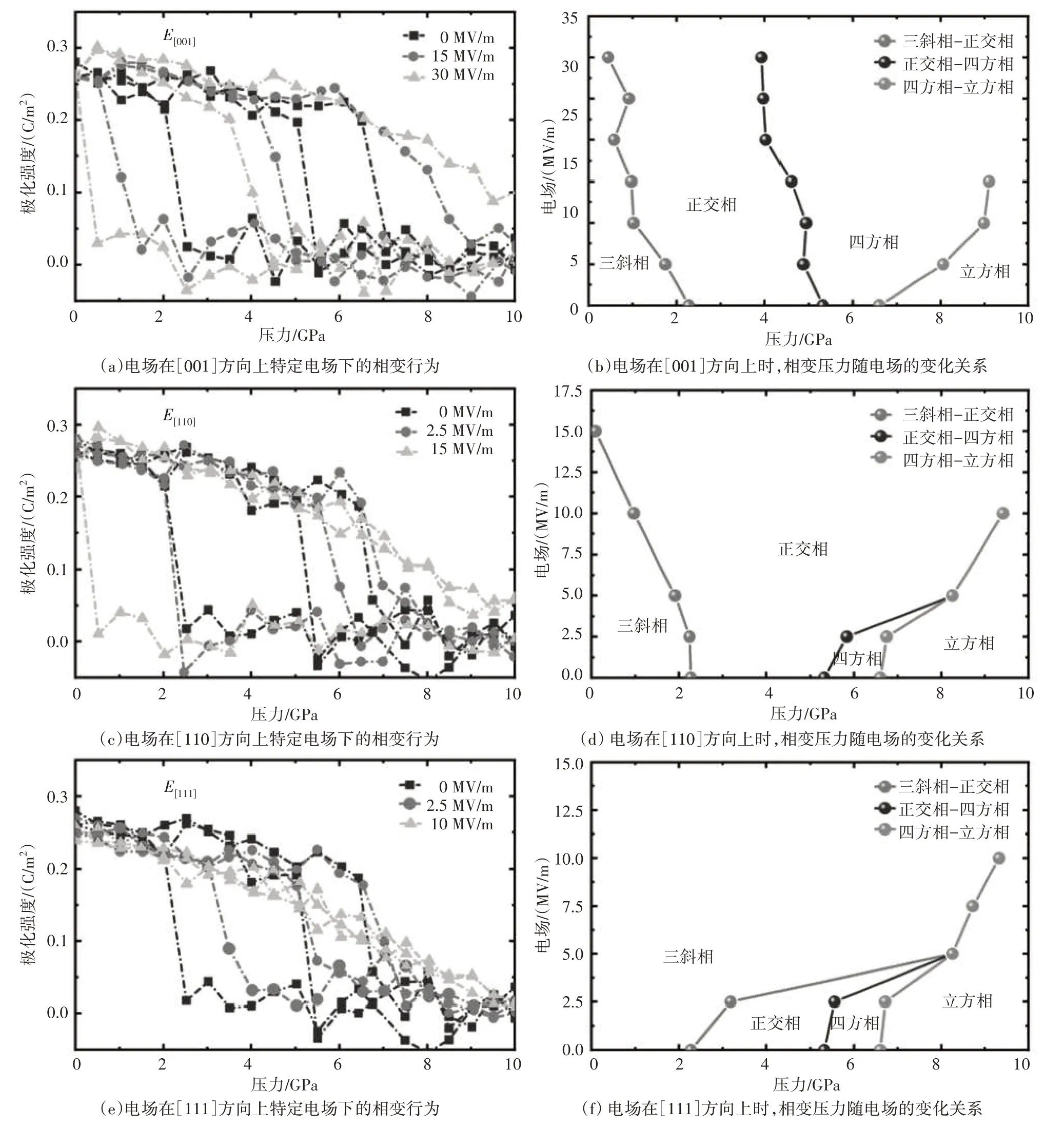
圖4 電場—壓力相圖

KNbO3在特定電場下的相變行為如圖4（a）、4（c）、4（e）所示，研究表明在不同電場下，相變壓力會向更高或更低的壓力偏移。為了清楚地描述相變壓力隨電場的變化情況，在［001］、［110］和［111］方向上施加電場時，相變壓力隨電場大小變化的關系如圖4（b）、4（d）、4（f）所示。如圖4（b）所示，當在［001］方向上施加電場，電場大小從0 MV∕m 升高到30 MV∕m時，鐵電三斜相（R）向鐵電正交相（O）轉變的相變壓力和鐵電正交相（O）向鐵電四方相（T）轉變的相變壓力都隨著電場的增大而減小，鐵電三斜相（R）和鐵電正交相（O）消失的最強電場遠高于在模擬過程中施加的最高電場，最后只有鐵電四方相（T）存在。如圖4（d）所示，當在［110］方向上施加電場，電場大小從0 MV∕m 升高到15 MV∕m 時，鐵電三斜相（R）向鐵電正交相（O）轉變的相變壓力隨著電場的增大而減小；當電場大小為15 MV∕m 時，鐵電三斜相（R）消失，鐵電正交相（O）到鐵電四方相（T）轉變的相變壓力隨著電場的增大而增大；當電場大小為5 MV∕m 時，鐵電四方相（T）消失，這個現象在電場—壓力相圖中可以被預測到，最后只有鐵電正交相（O）存在。如圖4（f）所示，當在［111］方向上施加電場，電場大小從0 MV∕m升高到10 MV∕m時，鐵電三斜相（R）向鐵電正交相（O）轉變的相變壓力和鐵電正交相（O）向鐵電四方相（T）轉變的相變壓力都隨著電場的增大而增大。當電場增加到5 MV∕m 時，鐵電正交相（O）與鐵電四方相（T）都消失，這個現象在電場—壓力相圖中也可以被預測到，最后只有鐵電三斜相（R）存在。

3 結語

本研究利用分子動力學模擬來研究KNbO3在壓力作用下的相變行為。通過分析極化強度和晶格參數隨壓力的演變行為獲得KNbO3的相變壓力依次為2.28 GPa、5.32 GPa、6.61 GPa；同時發現KNbO3在壓力作用下的相變行為也存在滯后現象。研究表明，鐵電正交相（O）和鐵電四方相（T）的兩相共存區的壓力區間為4.98～5.32 GPa，鐵電四方相（T）和順電立方相（C）的兩相共存區的壓力區間為6.19～6.61 GPa。研究了KNbO3相變壓力的尺寸效應，只有當原子數超過60 000 時，才能獲得宏觀上穩定的相變壓力。分析了電場對相變壓力的影響，電場的大小和方向對相變壓力都有顯著的影響，在電場的作用下，相變壓力會向更高或者更低的壓力點偏移，這為調控KNbO3的結構和性能提供了有意義的指導。