基于PCA-BP算法的機械鉆速預測研究*

湯 明 王漢昌 何世明 張光福 孔令豪

(西南石油大學油氣藏地質及開發工程國家重點實驗室)

0 引 言

機械鉆速(ROP)是反映鉆井效率的重要指標。為優化鉆井相關作業，降低鉆井成本，需要準確預測機械鉆速，到達實時優化的目的。精確建立機械鉆速與影響因素之間的模型，對預測機械鉆速、優化工程參數具有重大意義。

鉆速預測模型分為：①基于鉆速方程的預測模型。基于物理過程，針對不同參數與鉆速的關系，建立數學模型預測鉆速。例如F.S.YOUNG[1]建立鉆壓、可鉆性、轉速、鉆頭磨損系數以及進尺與機械鉆速之間的量化關系。M.K.MORAVEJI等[2]在傳統鉆速方程基礎上引入機械參數、水力參數和流變參數等6個量優化鉆速方程。LI W.Y.[3]基于分形理論修正鉆速方程，提高預測精度。U.J.F.AARSNES等[4]通過引入巖石力學參數、壓力和水力參數，修正鉆速預測模型。N.BILIM等[5]基于巖石可鉆性，建立巖石單軸抗壓強度、密度、硬度、孔隙度與機械鉆速的數學模型。G.HARELAND等[6]基于切削齒和巖石的相互作用，建立了機械鉆速與切削齒數量、切削面積和鉆頭直徑之間的關系，為鉆頭選型提供了參考思路。DENG Y.等[7]使用巖石動態抗壓強度代替靜態抗壓強度，提高牙輪鉆頭鉆速預測模型的精度。②基于機器學習的鉆速預測模型。基于現場大數據，M.C.SEIFABAD等[8]利用模糊類的機器學習算法，建立了Ahvaz油田不同層位的鉆速回歸模型，但該模型的普適性和泛化性較弱，僅僅適用于Ahvaz油田。為提高模型預測精度和泛化性，ZHOU Y.等[9-13]歸納了神經網絡(ANN)、支持向量機(SVM)、支持矢量回歸(SVR)、極端機器學習(ELM)和梯度增強決策樹(GBDT)等算法在鉆井工程中的適用性，提高了不同情況下對應模型的泛化能力和可靠性。

上述用于預測機械鉆速的鉆速方程模型存在建模困難、求解困難和對井場大數據利用率低下等問題。基于機器學習的鉆速預測模型存在模型輸入層參數過多，尋找隱藏層最優的節點數困難、計算成本高、預測結果穩定性差且無法實現實時反饋參數合理性等問題。為實現鉆速準確高效預測，本文提出一種基于主成分分析(Principal Component Analysis，PCA)[14]優化的BP(Back Propagation)神經網絡機械鉆速預測新模型。該模型以現場數據為基礎，首先采用小波濾波法對數據進行降噪處理，其次采用PCA提取數據集主成分，降低輸入層參數個數，縮小隱藏層節點數的尋找范圍，并將主成分作為模型輸入參數，預測機械鉆速。最后，基于預測結果實時反饋參數合理性并加以調整，以期為提高機械鉆速提供科學的指導意見。

1 基于主成分分析的BP神經網絡

基于主成分分析法，對BP神經網絡輸入層參數進行降維，有利于縮小隱藏層最優節點數的尋找范圍，降低計算成本，優化模型計算過程，提高模型預測結果的穩定性。

1.1 主成分分析法(PCA)

主成分分析屬于降維算法，目的是將多個變量指標類型轉化成少數幾個主成分，且這些主成分是原始變量的最大線性無關組合，因此能代表原始數據的絕大部分信息。主成分分析原理是將離散的數據點(信息)盡可能地集中在一個方向(本質為找出數據中心，旋轉坐標軸)，并以該方向的信息作為描述系統內離散數據點的主要特征。以二維情況為例，原始變量為x1、x2，由二維正態分布可知，樣本點分布在一個平面橢圓內。若長軸方向取F2，短軸方向取F1，效果相當于將原坐標軸按照一定角度進行旋轉，使更多的樣本點都分布在坐標軸方向，如圖1所示。

圖1 主成分幾何關系圖Fig.1 Geometric relationship of principal components

由圖1可以看出，坐標旋轉后有如下性質：①新坐標F1、F2非相關。②平面樣本點的波動可以歸結為F2軸上的波動，而F1軸上波動較小，稱F1、F2為x1、x2的主成分。若橢圓長徑遠大于短徑，則短徑上的綜合變量F1可忽略不計，可只考慮長徑(F2)方向的波動，因此二維平面可降維成一維線性，故F2即為x1、x2的主成分。③基于數學角度，找出主成分即為找出樣本數據集較大特征值對應的特征向量。

1.2 BP神經網絡

BP神經網絡的原理是通過修正實際值和預測值之間的誤差，通過反向調節機制改變神經網絡的權值和閾值，使預測值不斷接近實際值。如果誤差較大，則重新選擇連接權值進行計算，直到誤差滿足要求。該方法解決了隱藏層不易確定的問題，具有較強的實用價值。

1.3 PCA-BP模型

機械鉆速受到眾多因素綜合影響，利用PCA方法可有效降低多影響因子間的冗余程度，從而獲得機械鉆速與影響因子間的本質關系，然后將數據集主成分作為BP神經網絡的輸入參數，進行機械鉆速預測。

PCA優化BP神經網絡算法步驟如圖2所示。

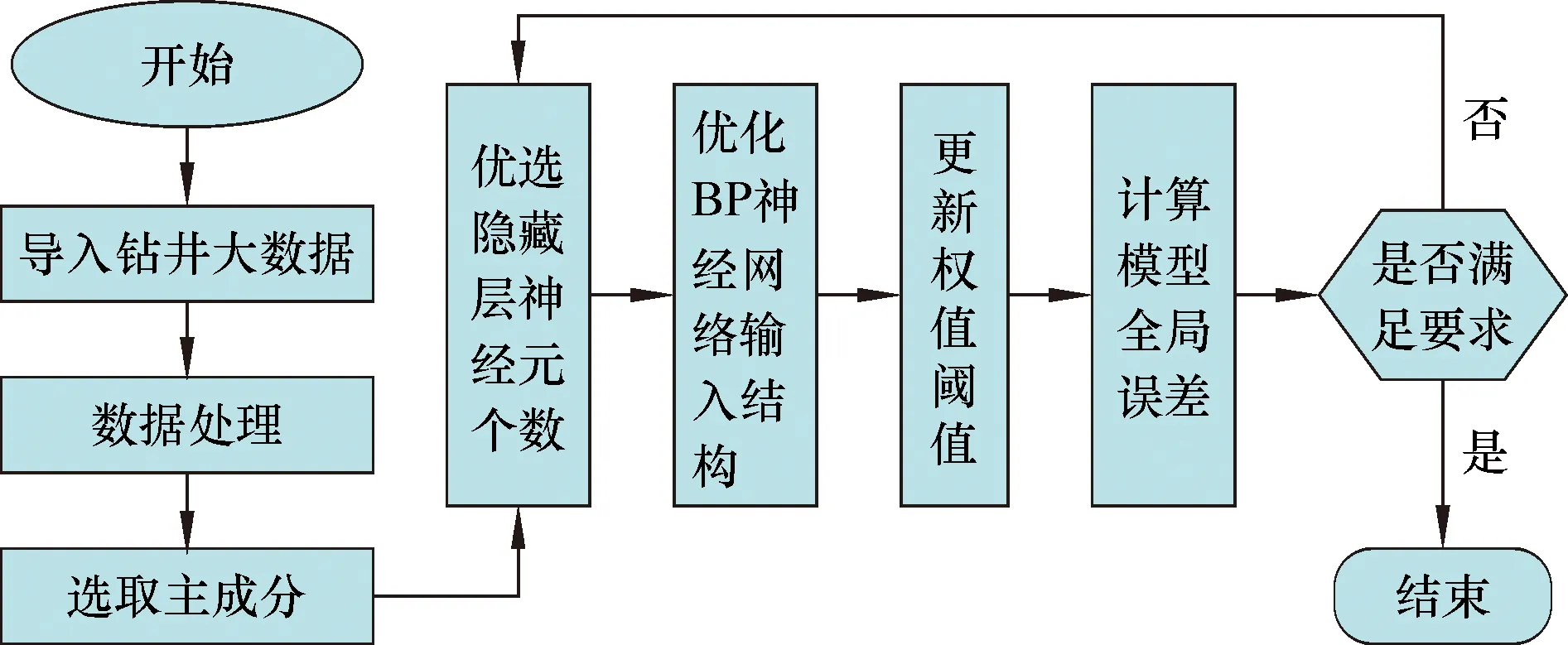
圖2 基于PCA優化的BP神經網絡機械鉆速預測模型流程圖Fig.2 Flow chart of ROP prediction model based on PCA-BP

2 基于PCA-BP的機械鉆速預測建模

基于PCA-BP的機械鉆速預測建模步驟具體為：首先對鉆井大數據進行預處理，清洗掉數據中的異常值、錯誤值等；其次對后處理數據進行主成分分析，降維輸入層參數，縮小隱藏層神經元最優節點數的尋找范圍；最后以數據集主成分作為BP神經網絡的輸入參數，機械鉆速作為輸出參數，進行機械鉆速的預測研究。

2.1 鉆井數據預處理

井場中通過數字電路傳輸錄、測井等數據。由于高頻數字電頻的影響，信號中會出現大量帶有尖峰或突變的異常“噪聲”，為提高原始數據中信息利用率，需除去噪聲干擾成分[15-18]。小波濾波法同時具備“局部化、窗口大小隨頻率變換”的優點，可對高頻部分“高時間分辨率、低頻率”影響產生的白噪聲進行有效去除。將分析信號X(t)作為小波變換，即有：

(1)

式中：Wf(τ，a)為經過小波變換后的去噪數據；a(a>0)為尺度因子，作用是實現基本小波φ(t)的伸縮變換；τ為平移因子，作用是實現基本小波在時間軸上的平移變換。

2.2 主成分分析

現場數據種類繁多冗雜，數據之間大多為非線性關系，為便于計算和現場簡化應用，采用主成分分析對數據降維，簡化計算。PCA方法的計算步驟如下。

步驟1：標準化處理。假設有n個樣本，p個指標，則可以構成大小為n×p的樣本矩陣x：

(2)

對式(1)按列計算均值再求標準差，得到數據集標準陣：

(3)

(4)

式中：Sj為變量j的標準差。

對數據進行標準化處理：

(5)

式中：Xij為變量j的標準化數據。

故原始樣本矩陣經標準化后變為：

(6)

步驟2：計算標準化樣本的協方差矩陣并求對應的特征值和特征向量。

(7)

(8)

式中：rij為變量標準化后的協方差；R為數據集的協方差矩陣。

計算特征向量：

(9)

式中：λi為協方差矩陣的特征值；ap為協方差矩陣的特征向量

步驟3：計算主成分貢獻率及累計貢獻率。

(10)

(11)

式中：contribution為主成分貢獻率；contribution_sum為主成分累計貢獻率。

步驟4：分析主成分代表意義。在實際應用中，主成分的選取原則為，選取累計貢獻率超過80%的特征值對應的第一、第二、……、第m(m≤p)個主成分[19-20]。

第i個主成分為：

Fi=a1iX1+a2iX2i+…+apiXp(i=1，2，…，m)

(12)

2.3 PCA-BP機械鉆速預測建模

PCA-BP機械鉆速預測模型框架結構如圖3所示。PCA-BP機械鉆速預測模型建模過程共分為4個部分：第一個部分為數據預處理部分，作用是收集整合現場實測數據并對數據進行降噪，提高數據可信度；第二部分為數據主成分分析部分，其目的是完成數據集的主成分分析，簡化數據結構；第三部分為BP神經網絡的結構確定與訓練部分，該部分的輸入變量為第二部分中計算所得數據集主成分，輸出變量為機械鉆速；第四部分為預測誤差分析和效果評價，若預測誤差精度達到精度要求，則輸出預測結果、保存訓練網絡，并將PCA-BP模型與傳統的BP模型進行橫向對比，反之則調整網絡結構，直到達到精度要求并進行模型的橫向對比。

3 實例分析

大多數機械鉆速類研究均以單井鉆速作為預測，泛化性差，因此為增強模型泛化性，需擴大訓練數據的范圍。本次建模預測選用某區塊6口井(J1～J6井)的二開一趟鉆數據作為訓練集數據，數據量為13 678組。

3.1 參數預處理

本次實例數據來自四川盆地川中地區J井區，對完鉆井中的錄井、測井數據加以分析，篩選出鉆壓、扭矩、轉速、排量、密度、切削深度、彈性模量、機械鉆速等8組數據。表1列舉了J1～J6井部分訓練數據。

鉆井現場環境復雜多變，使得數字電路中存在白噪聲的干擾，現利用濾波法對數據進行降噪處理，以J2井部分數據集處理結果為例，如圖4所示。

在圖4中，不同參數原始數據曲線包含許多尖峰狀的異常值，應用濾波法降噪后，數據曲線光滑且輪廓清晰，數據曲線中的尖峰狀異常值被有效消除。

3.2 J井區影響鉆速的主成分

將濾波后的數據進行主成分分析，其相關系數矩陣的特征值、對應的特征向量以及貢獻率和主成分如表2所示。

表2 相關系數矩陣特征向量Table 2 Correlation coefficient matrix eigenvector

從表2可以看出，前4個主成分的累計貢獻率達92.6%，因此可以考慮只取前面的4個主成分代表原始數據特征。數據集主成分如表3所示。

表3 數據集主成分Table 3 Principal components of data set

數據集主成分及其載荷為：

Fi=X·λi(i=1，2，3，4)

(13)

F1～4=[X1X2X3X4X5X6X7]

(14)

第一主成分F1在鉆壓、扭矩、轉速上有中等成分的正載荷，而在切削深度上有中等程度的負載荷，其余變量上載荷都較小，可稱第一主成分為機械參數成分。

第二主成分F2在彈性模量上有較大程度的正載荷，在密度上有較大程度的負載荷，其余變量上載荷都較小，可稱第二主成分為地層因素成分。

第三主成分F3在排量上有較大程度的正載荷，在彈性模量上有中等程度的負載荷，其余變量上載荷都較小，可稱第三主成分為水力參數成分。

第四主成分F4在密度上有中等程度的正載荷，在彈性模量上有較大程度的負載荷，在扭矩、排量、密度上有中等程度的負載荷，其余變量上載荷都較小，可稱第四主成分為密度因素成分。

3.3 機械鉆速預測及誤差分析

PCA-BP模型的數據集按照訓練集80%、驗證集20%的方式送入模型訓練，設置誤差精度為0.001，迭代次數為8 000，學習速率為0.01。測試集和訓練集精度如圖5所示。

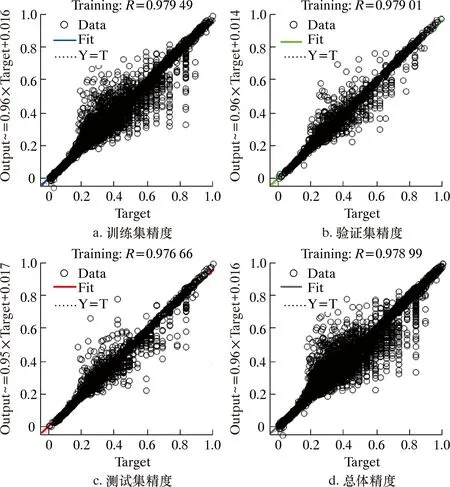
圖5 PCA-BP模型驗證圖集Fig.5 Collective drawings of PCA-BP model verification

BP神經網絡精度受隱藏層數和隱藏層節點數影響，故提高網絡預測精度方法有2種：①增加隱藏層數；②優選隱藏層節點數[21-26]。增加隱藏層可提高計算精度，但隨著隱藏層的增加，網絡訓練時間和過擬合概率將會大大增加。因此本文采用優選隱藏層節點數的方式提高網絡預測精度。隱藏層神經元個數受到輸入層參數的影響，以Kolmogorov和Gorman[27]分別作為隱藏節點數上、下限，做出不同輸入參數數量下的隱藏層神經元節點數和節點數對應的誤差曲線圖，如圖6、圖7所示。從圖6可知，輸入層參數范圍為[1，7]，隱藏層神經元范圍為[1，15]，可見隱藏層神經個數優選范圍較大。但是通過主成分降維后，不僅可保留大部分原始數據的有效信息，還可有效縮小最優節點數的尋找范圍。由圖6和圖7可知：隱藏層節點數為7，對應誤差最小僅為0.000 232；輸入參數個數為3，代表原始變量84.8%的信息，對應隱藏層神經元范圍為[3，7]；輸入參數個數為4，代表原始變量92.6%的信息，對應隱藏層神經元范圍為[3，9]。綜合考慮網絡誤差和原始變量信息反映程度，選擇輸入層參數個數為4，隱藏層節點數為7。

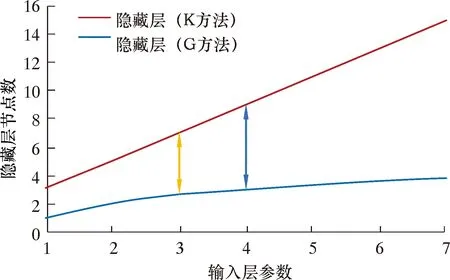
圖6 輸入參數個數與節點數關系Fig.6 Relation between input parameters and nodes

圖7 節點數與誤差關系圖Fig.7 Relation between node number and error

其中，Kolmogorov法為：

h=2m+1

(15)

Gorman法為：

h=log2(2m)

(16)

式中：h為隱藏層神經元個數；m為輸入層神經元個數，適用于單層網絡的隱藏層節點數確定。

圖8為機械鉆速預測結果橫向對比。圖9為不同模型誤差頻率分布。從圖8和圖9可以看出，PCA-BP模型的預測結果相較于BAS-BP、BP和RF的預測結果，真實值和預測值間的符合度更高，變化趨勢更接近，并且模型預測產生的誤差更小。其中PCA-BP模型誤差在10%以內的頻數占比為90.74%，由此可見該模型預測結果的誤差大多數都在10%以下。而BAS-BP、BP和RF在10%以內的誤差頻數占比為80.9%、77.2%和69.5%，表明計算精度相較于PCA-BP明顯降低；在10%～30%內的誤差頻數占比分別為14.1%、13.1%和20.4%，相較于PCA-BP其誤差頻數占比分別增大7.81%、6.81%和14.11%。由此可見，PCA-BP模型誤差范圍更小、預測精度更高、適用性更強。

圖9 不同模型誤差頻數占比分布圖Fig.9 Different models error frequency and prcentage layout

為驗證PCA-BP模型相較于BAS-BP、BP和RF模型的優越性，在預測結果和誤差統計的基礎上，選取擬合優度(R2)、均方根誤差、平均絕對百分比誤差和迭代次數作為評價模型的指標[28-29]，橫向對比各模型的優勢，結果如表4所示。

表4 不同模型評價指標Table 4 Evaluation indices of different models

在表4中，PCA-BP模型的迭代次數與BAS-BP相同，但其均方根差和平均絕對百分比誤差較BAS-BP模型分別降低23.88%和35.45%，擬合優度提高5.7%，表明在算力接近的情況下，PCA-BP的預測精度高于BAS-BP。相較于BP模型，PCA-BP的均方根差、平均絕對百分比誤差和迭代次數分別降低30.3%、56.7%和73.0%，擬合優度提高9.4%；相較于RF模型，分別降低43.6%、61.5%和88.7%，擬合優度提高18.7%。以上分析表明，本文提出的PCA-BP機械鉆速預測模型預測精度高，迭代速度快，便于應用。

3.4 影響機械鉆速的參數實時評價

基于機械鉆速預測結果，開展影響機械鉆速的參數實時評價，如表5中所示的A、B和C這3點位于水平段(2 550～3 340 m)，可以看出機械鉆速變化較大。A點到B點，機械參數成分加強，水力參數成分減弱，其他成分變動較小，機械鉆速降低；B點到C點，機械參數成分減弱，水力參數成分加強，其他成分變動較小，機械鉆速升高。由此可見，水平段中水力參數成分是導致機械鉆速變化的主要原因，增大水力參數有利于提高機械鉆速。

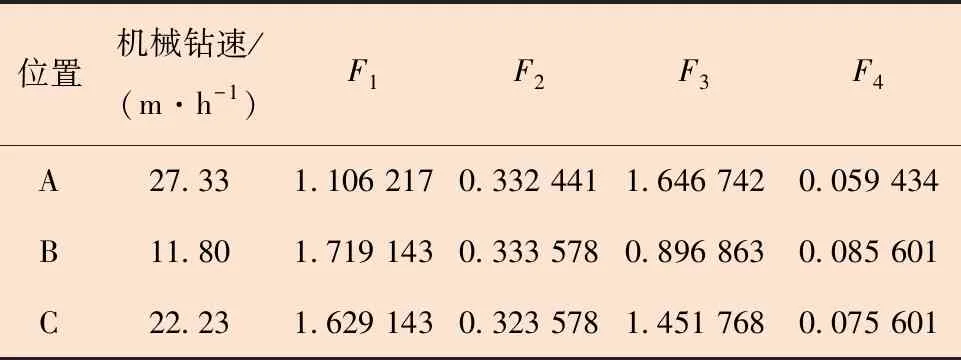
表5 不同鉆速下的主成分Table 5 Principal components at different ROPs

4 結 論

(1)以J井區為例，采用主成分分析法，選取4個主成分，可涵蓋92.6%的原始數據特征，能有效降低數據集的維度，節省大量的計算時間，提高數據集使用效率。

(2)基于PCA-BP神經網絡，建立機械鉆速預測模型，與BAS-BP、BP和RF等智能算法相比：均方根誤差分別降低23.88%、30.3%和43.6%；平均絕對百分比誤差分別降低35.45%、56.7%和61.5%；擬合優度分別提高5.7%、9.4%和18.7%，表明PCA-BP模型預測精度高、迭代速度快。

(3)在實際鉆井過程中，基于PCA-BP算法的預測結果，反演任意井深下主成分中的工程參數對機械鉆速的影響，并以此為依據調整工程參數，可有效提高機械鉆速，提升鉆井效率。