帶塢艙船舶尾艙消浪裝置消浪性能研究
孫雷,楊雨田,韓易健,馬玉祥
(大連理工大學 a.船舶工程學院 b.水利工程學院,遼寧 大連 116024)
尾部半開敞式塢艙的船舶不論是在軍事領域,還是在工程建設領域,都能夠發揮出重要的作用。在正常作業時,其尾部的半開敞塢艙處于半浸沒狀態,形成與外部連通的自由液面。在外部波浪的作用下,艙內的自由液面會形成波浪,形成有害的波浪砰擊,影響艙內裝備的正常作業。因此,有必要對塢艙內水體的波浪消減和控制方法開展深入研究,需要提出一套適用于帶塢艙船舶尾艙內波浪特性的消浪裝置方案。
目前對半開敞液艙數值模擬的研究成果還比較少,且大多都基于計算流體力學(CFD)方法。Bass等[1]采用Flow-3D 對4 級海況作用下具有半開口液艙的登陸平臺進行了模擬,并分析了平臺艙口的運動狀況和艙內的波高情況。Cartwright 等[2]采用SPH 方法對具有半開口液艙的登陸平臺進行了模擬。胡曉慶[3]對Wigley 船型進行了改造,增加了尾部船塢,之后用Fluent 對該船型進行了一系列的數值模擬,發現船體運動是否受到約束對船艙內的流場波浪波面起伏具有很大的影響,并指出對尾艙內進行合理的消浪裝置設計具有重要意義。物理模型試驗也是研究復雜水動力問題的必要手段[4]。目前關于半開敞式液艙的物理模型試驗還比較少,對于液艙問題的研究多為液艙晃蕩試驗[5]及月池試驗[6]。Hopman 等[7]以荷蘭海軍登陸艦為原型進行了4 級海況下艙內流體運動的物理模型試驗,發現艙內波面運動幅度與波浪周期有關。翁歡英[8]對不封閉艙容內部消波裝置的設計選型進行了試驗研究。Zheng 等[9]采用了變態比尺的方法(水平與垂直方向的比尺不同),在試驗水池的深度有限的情況下,對港灣共振問題進行了研究。在使用變態比尺進行模型試驗時,需要對原模型與變態比尺后的模型進行相似條件的驗證[10]。
國內外學者一直致力于消浪裝置的研究,對消浪裝置的研究通常從理論研究、物理模型試驗和數值模擬等3 個方面展開。理論研究方面,Ursell 等[11]在有限水深情況下,對直立擋板進行了研究,給出了透射系數的計算公式。Heins[12]研究了水平板在有限水深水域的水面處的透射系數。Stoker 等[13]對單塊水平板在長波作用下的消浪性能進行了研究。Siew 等[14]研究了下潛式水平板,用簡單形式的方程描述了其在長波作用下的反射系數和透射系數。物理實驗研究方面,Paterapanich 等[15]進行了物理模型試驗,對水平板的板寬和水深等參數進行了研究。Murakami 等[16]對斜板式消浪裝置進行了研究。Liu 等[17]研究了潛式雙層水平板消浪結構。王國玉等[18]利用物理模型試驗的方法研究了二維規則波作用下開孔斜板的消浪性能。數值模擬方面,Yu 等[19]基于勢流理論研究了帶孔水平板上的波浪運動,討論了不同因素對其能量損耗的影響。Carter 等[20]研究了波浪經過平板結構時平板下方的逆流現象。Guan 等[21]研究了不同型式擋板的制蕩消波作用。Cho[22]利用ALE 有限元方法對燃料儲罐結構內擋板的抑制作用進行了研究。Zang 等[23]得出了多孔擋板的長度、孔隙率等因素對波浪的影響。丁俊杰等[24]利用CFD 方法對透水式多層開孔板進行了數值模擬研究,研究了消浪裝置的反射系數和透射系數與入射波波長和波高的關系。任冰等[25]基于VOF 方法,模擬研究了海綿層結構在水池實驗中的消浪系數。
綜上所述,目前對于半開敞液艙的研究成果較少,主要方法為CFD 數值模擬和物理模型試驗。消浪裝置的研究已經非常豐富,有眾多學者在這一領域進行開拓性的研究。其中,數值模擬由于其低廉的成本、可靠的求解結果,在工程領域得到了廣泛的應用。本文針對荷蘭皇家海軍兩棲運輸船,使用多孔擋板為基礎,給出了開孔板消浪裝置的選用與布置方案,并使用CFD 方法模擬帶有消浪裝置方案的船舶響應,監測船舶的運動響應和艙內多個監測點的波高情況,評估給出的消浪裝置方案的消浪性能。
1 理論及數值方法
1.1 基礎理論
1.1.1 基本控制方程
本文數值模型的建立是基于不可壓縮黏性流體的基本假定。流體運動遵循質量守恒定律、動量守恒定律和能量守恒定律。
1)連續性方程(質量守恒方程)。連續性方程指出流體在流經某一控制體時,流入控制面與流出控制面的流體質量之差,必然等于該控制體的流體質量增量,見式(1)。
式中:V為流體微元控制體;A為流體微元控制體的表面(也稱控制面);t為時間;ρ為流體密度;v→為控制面上的流體速度矢量;n→為流體控制面上一點的法向單位矢量。表達式在直角坐標系下的微分方程見式(2)。
式中:x、y和z為流體位置坐標值;u、v和w為流體在x、y和z方向上的速度分量。可將式(2)進一步寫成張量形式:
對于不可壓縮流體,密度ρ為常數,式(3)可簡化為:
2)N-S 方程(動量方程)。動量方程表明單位體積控制體內流體動量的時間變化率等于作用其上的力,見式(5)。
式中:fx、fy和fz分別為體積力在x、y和z方向上的分量;p和τ為流體表面力的法向應力分量和切向應力分量。當引入平衡壓強即靜水壓強,并引入Stokes 假定(法向應力和切向應力與線應變率和角變形率呈線性關系)時,動量方程(5)轉化為N-S 方程,其表達式張量形式:
當忽略黏度時,表達式簡化為式(7)。
其分量形式:
3)能量守恒方程。能量守恒代表控制體中能量的增加等于外力對其做的功,見式(9)。
或寫成:
式中:T為溫度;Cp為流體的比熱容;k為傳熱系數;ST為黏性耗散項。
1.1.2 拓展型緩坡方程
當艙門開敞時,尾部塢艙為半封閉環境水域。對于尾部塢艙內的水體晃蕩,波浪于船底底部的透射可以看作一種能量損耗,只影響水體晃蕩的強度,而不改變艙室水體運動的固有頻率。此外,艙室水體是在不透水的底邊界和垂向艙壁邊界的約束下運動的,與港灣振蕩現象最為接近。因此,可采取廣泛應用于港灣振蕩研究的拓展型緩坡方程模型(EMSE)進行尾部塢艙內水體的固有頻率和波浪運動形態的計算。緩坡方程控制方程見式(11)。
式中:?為平面微分算子,?=(?/ ?x,?/?y);φ為速度勢;k、C和cg分別為波數、波浪相速度和群速度,它們由以下式(12)和(13)決定。
式中:h為水深。控制方程和邊界條件構成封閉的方程組后,才能對物理現象進行合理的描述。
在水體共振研究中,常用的邊界為混合元邊界,其表達式為:
1.2 數值模擬
本文采用荷蘭皇家海軍兩棲運輸船[7],其主尺度參數見表1。本文對船舶進行等比例建模,船舶實體及船體幾何模型如圖1、圖2 所示。其中,為了方便計算與后續分析,本文對該船舶的尾部艙室進行了簡化。由于船舶原艙室在艙內靠近首端部分有一個上升的斜坡,因此將船艙分成了2 個不同高度的部分。本文將艙室簡化為簡單的長方體,其中艙長為52 m,艙寬為15 m,艙內水深為1.2 m。

圖2 船舶模型Fig.2 Ship model

表1 船舶主尺度參數Tab.1 Main dimension parameters of ship

表2 半開敞狀態下艙內水體固有周期Tab.2 Natural period of water body in cabin under semi-open state
用EMSE 模型計算尾部塢艙內水體的固有頻率和波浪運動形態。艙室的響應曲線和固有模態的周期如圖3 所示,4 個固有周期的瞬時波面如圖4 所示。
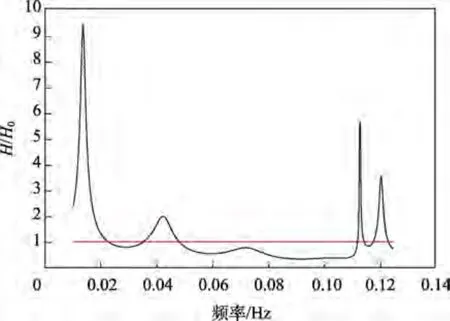
圖3 半開敞艙室響應曲線Fig.3 Response curve of semi-open cabin
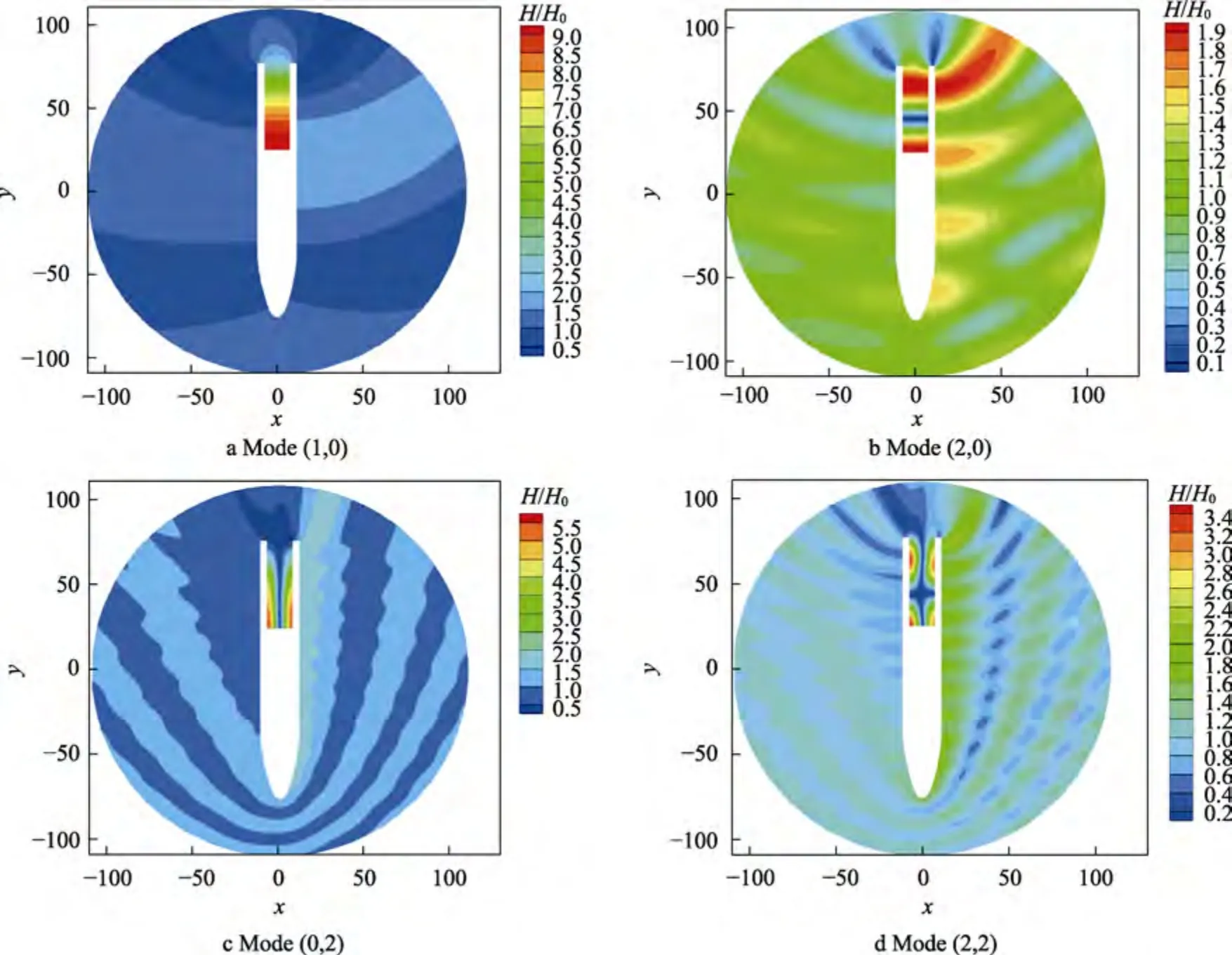
圖4 固有模態瞬時波面Fig.4 Natural modal instantaneous wave surface
本文對該船舶模型進行計算,得到其縱搖、垂蕩和液艙耦合共振周期為 11.393 4 s。該船舶的縱搖RAO 曲線如圖5 所示。
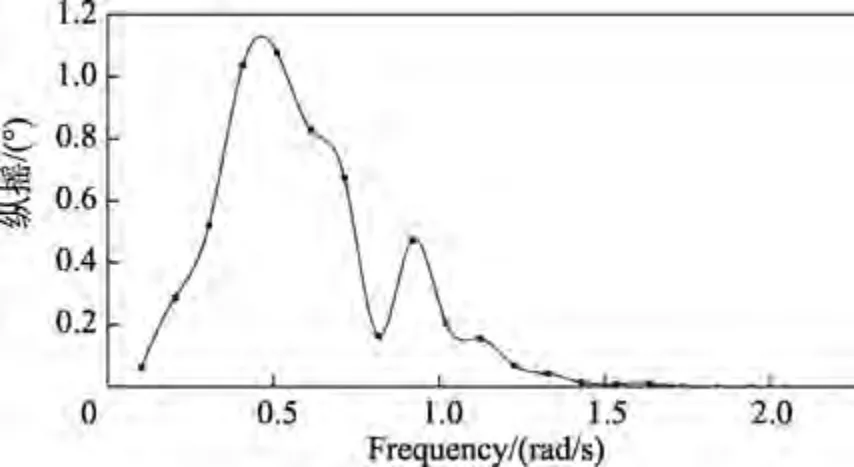
圖5 縱搖RAO 曲線Fig.5 Pitch RAO curve
本文在基于CFD 數值模擬軟件Star-CCM+中的網格劃分及網格收斂性驗證基礎上,分別采用網格基礎尺寸為15、25、35 m 等3 種不同的網格尺寸進行模擬(如圖6、圖7 所示),其中網格尺寸為25 m 的網格總量約為500 萬。輸出船舶的縱搖時程曲線(如圖7 所示),可以看出,網格基礎尺寸為25 m 時已經達到收斂,故采取基礎尺寸為25 m 的網格劃分方案。
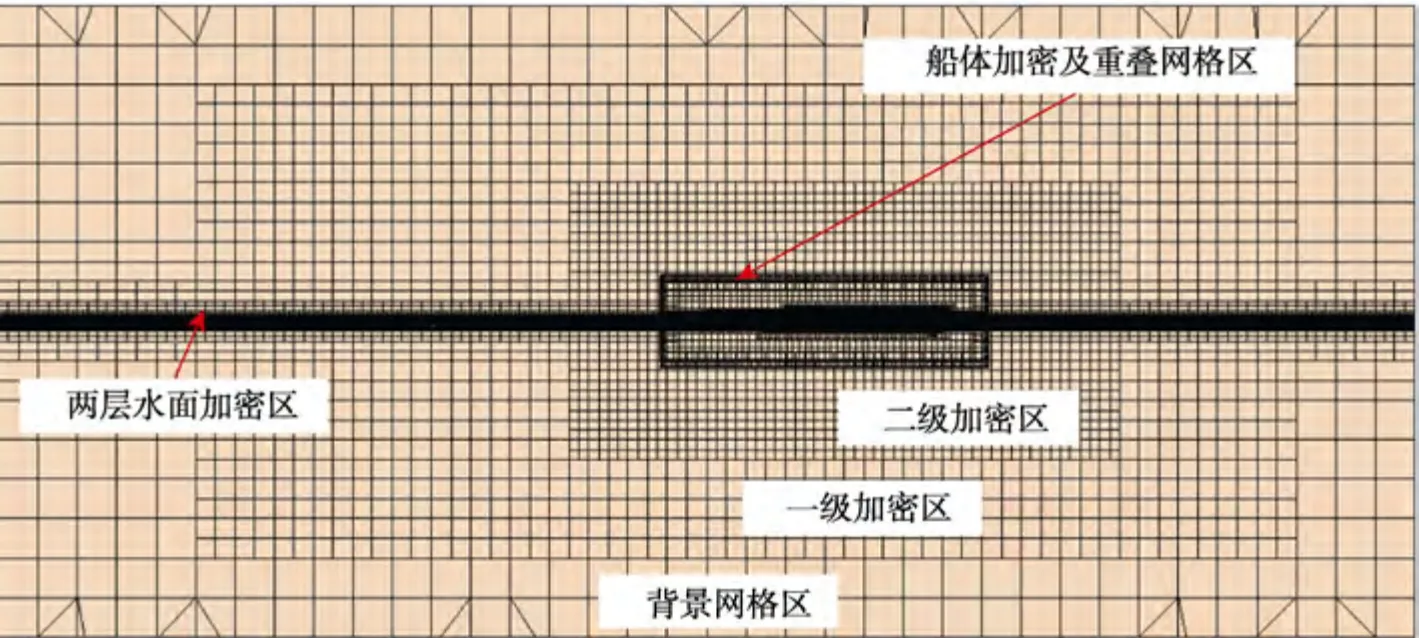
圖6 流域網格劃分Fig.6 Watershed grid division
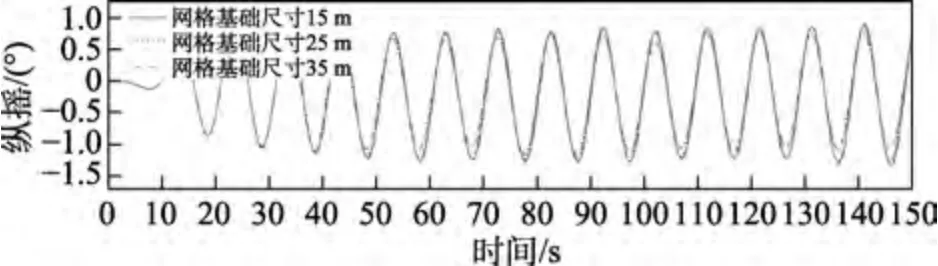
圖7 3 種不同尺寸網格結果對比Fig.7 Comparison of grid results of three different sizes
經過分析,本文在荷蘭皇家海軍兩棲運輸船的塢艙內分別設置了如下4 種方案。
方案一:不設置消浪裝置的空艙對照組,如圖8a 所示;
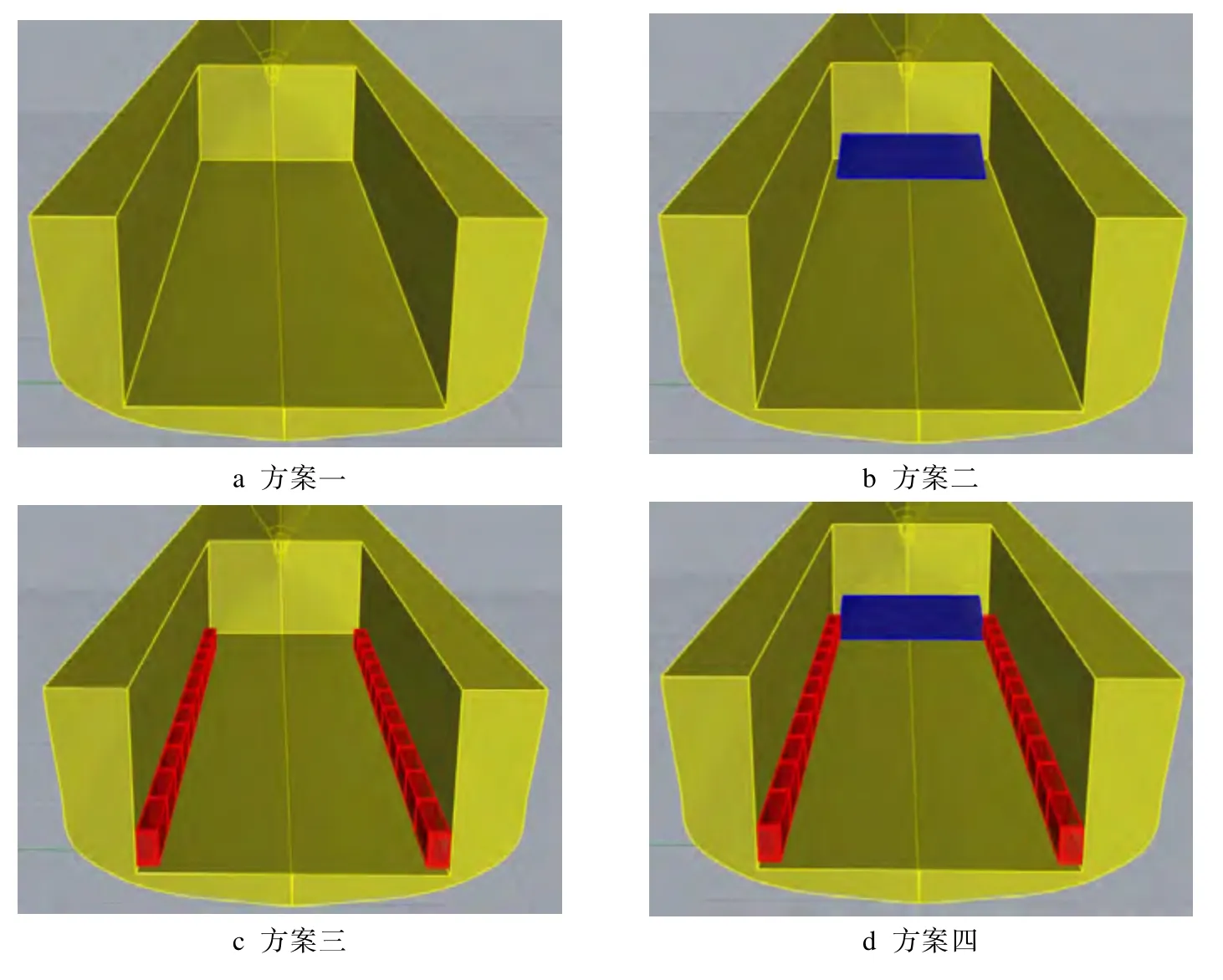
圖8 不同布置方案模型Fig.8 Models of different layout schemes:a) scheme 1;b) scheme 2;c) scheme 3;4) scheme 4
方案二:僅布置首端開孔板消浪裝置,孔隙率為7.4%,如圖8b 所示;
方案三:僅布置側壁開孔板消浪裝置,孔隙率為8%,如圖8c 所示;
方案四:同時布置首端和側壁開孔板消浪裝置,孔隙率分別為7.4%和8%,如圖8d 所示。
本文采用多孔介質區域模型對多孔板結構進行等效替代,對由多孔板結構組成的消浪裝置進行CFD數值模擬。這種處理方法的優點在于無須考慮多孔板的細小空洞,節省大量計算資源。由于消浪裝置設置在艙室四周,且本身由多孔介質模型組成,因此不會對塢艙內設備的正常出入及工作產生不利影響,而且塢艙內水體的固有頻率也不會產生明顯的變化。
在液體流過多孔介質區域時會經歷一個降壓過程。達西定律將流速與基于滲透率測量的壓力梯度聯系起來,見式(15)。
式中:μ表示流體的分子黏度;kp表示滲透率(被認為是多孔介質的一種內在性質);vs是通過介質的表面速度。隨著流速的增加,流體流速與壓力梯度的關系將會變得非線性,于是有了Forchheimer 方程:
在STAR-CCM+中,對于多孔介質區域的描述便使用了Forchheimer 方程,在單項流中,流體的壓降Δp被定義為:
式中:vn為物面的法向速度;a和b為阻力相關系數;ρ表示界面處的流體密度。
多孔介質在流動方向上的長度L,將壓降轉換為壓力梯度:
式中:α為慣性阻力相關系數;β即黏性阻力相關系數。
為了驗證數值實驗方法的正確性,采用相同的慣性和黏性阻力系數,分別對多孔板和多孔介質區域進行模擬。選取與本文消浪裝置具有相同板厚與孔排布的正方形多孔板(如圖9 所示),其邊長為11.7 cm,圓孔的孔徑為0.8 cm,孔隙率約為29.7%,板厚為1 cm。在相同流域與流速情況下,多孔板與多孔介質區域得到的數據曲線對比如圖10 所示。

圖9 多孔板結構Fig.9 Porous plate model
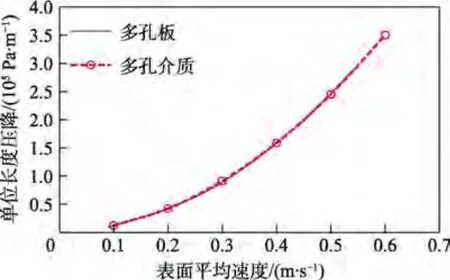
圖10 多孔斜板模型與多孔介質區域得到的數據曲線對比Fig.10 Comparison of data curves between porous inclined plate model and porous media region
為了定量地探究消浪裝置的消浪效果,在艙內x方向設置了24 個測點,y方向設置了7 個測點,共168 個測點。其中,x方向間隔 2 m,y方向間隔 2 m,原點在塢艙尾端開口與中縱平面交點處。每個監測點測得波面時程曲線,同時記錄艙內波面側視圖和三維視圖,用于后續分析,監測點示意圖如圖11 所示。波況設置見表3。

圖11 艙內監測點布置Fig.11 Layout of monitoring points in the cabin

表3 波況參數Tab.3 Parameters for different wave conditions
2 結果和討論
以波況1 為例,首先模擬對比了4 種方案的船舶運動響應,如圖12 所示。可以看出,消浪裝置的裝載對船舶的響應情況幾乎沒有影響。
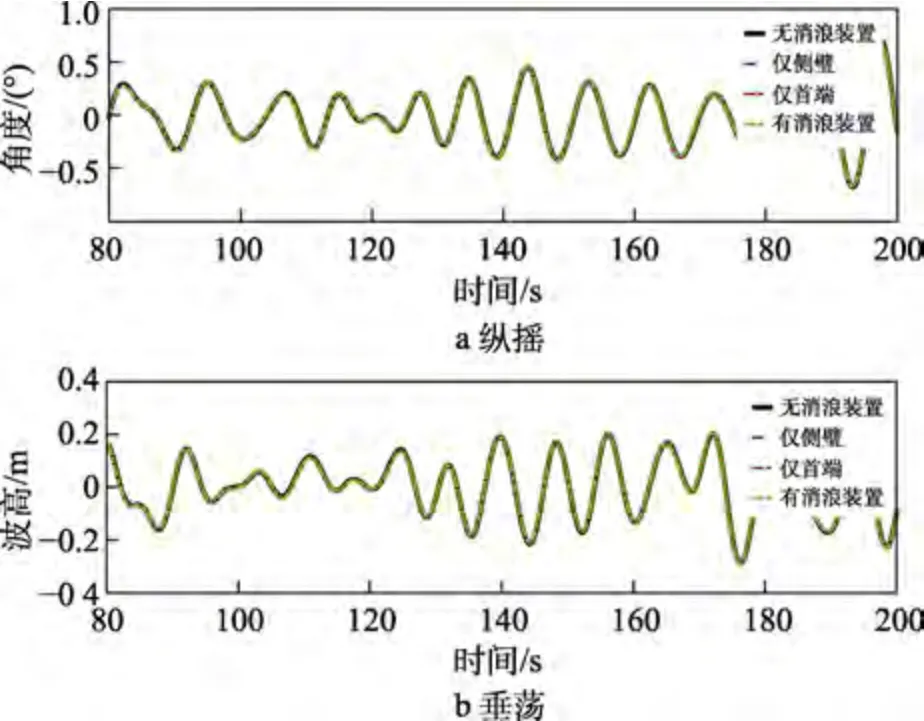
圖12 運動響應時程曲線對比Fig.12 Comparison of motion response time history curves:a) pitch;b) heave
第一個較為明顯的波浪在t=16.3 s 時到達船艙內部,如圖13 所示。可以看出,波浪從塢艙尾端開口傳至塢艙首端的過程中,在方案一、二中到達首端的波浪相較于方案三、四具有一個較為明顯的起伏。這說明側壁消浪裝置對于入射波具有一定的削弱作用,但這種減小作用是十分有限的,并不能將任意波高的波都完全消除。

圖13 t=16.3 s 艙內波面展示Fig.13 Wave surface in cabin when t=16.3 s:a) vertical view;b) partially enlarged view
從圖14 可以看出,在隨后的17.8 s,沒有首端斜坡板的方案一、三出現了較為明顯的反射波,而方案二、四則沒有反射波的出現。可以看出,僅具有一個斜板的消浪裝置便可以較好地消除反射波。之后,艙內便不斷有入射波和反射波生成,并且這些入射波和反射波相互作用會形成新的波,這導致艙內的波面變得十分復雜。方案二中,首端消浪結構可以減弱反射波,但并不能完全消除。方案三中,塢艙尾端開口形成的入射波在側壁裝置的作用下會逐漸減弱,但后面形成的波高較高的波并無法完全消除,依然會發生如反射波相匯的情況。方案四則很少看到有入射波與反射波相匯的情況,且波浪不斷衰減,如圖15 所示。

圖14 t=17.8 s 艙內波面展示Fig.14 Wave surface in cabin when t=17.8 s:a) vertical view;b) partially enlarged view

圖15 t=89.8 s 艙內波面展示Fig.15 Wave surface in cabin when t=89.8 s
波況1 在4 種方案下艙內監測點的波高時程曲線對比如圖16 所示。本文選取了幾個具有代表性的監測點進行展示,監測點具體位置在每個曲線圖的標題處標出,取波浪發展的80~200 s 時間段進行展示。從這些監測點中可以看出,相較于無消浪裝置的波面,3 個有消浪裝置的波面最大波高峰值明顯得到了削弱,并且同時具有首端和側壁消浪裝置的消浪效果要優于僅有首端消浪裝置和僅有側壁消浪裝置的情況。另外,不僅監測點的最大波高得到了削減,有消浪裝置相較無消浪裝置波面整體也明顯更加平緩,這使得艙內結構物受到的砰擊載荷更小,作業也更加安全。還可以看出,隨著監測點的x值向塢艙尾端開口處移動,消浪裝置的消浪效果也會漸漸減少,大約到x=30 m 處,消浪效果已經不太理想,說明本文給出的消浪裝置方案主要作用于尾艙內部區域。這是因為該消浪裝置的消浪機理為削弱入射波,并避免波浪與內壁的砰擊,而在塢艙尾端開口處,波浪由于船舶的響應和外域波浪的共同作用,入射波剛開始產生,此時波浪并未與消浪裝置發生作用,因此消浪裝置在塢艙尾端開口區域作用并不大。
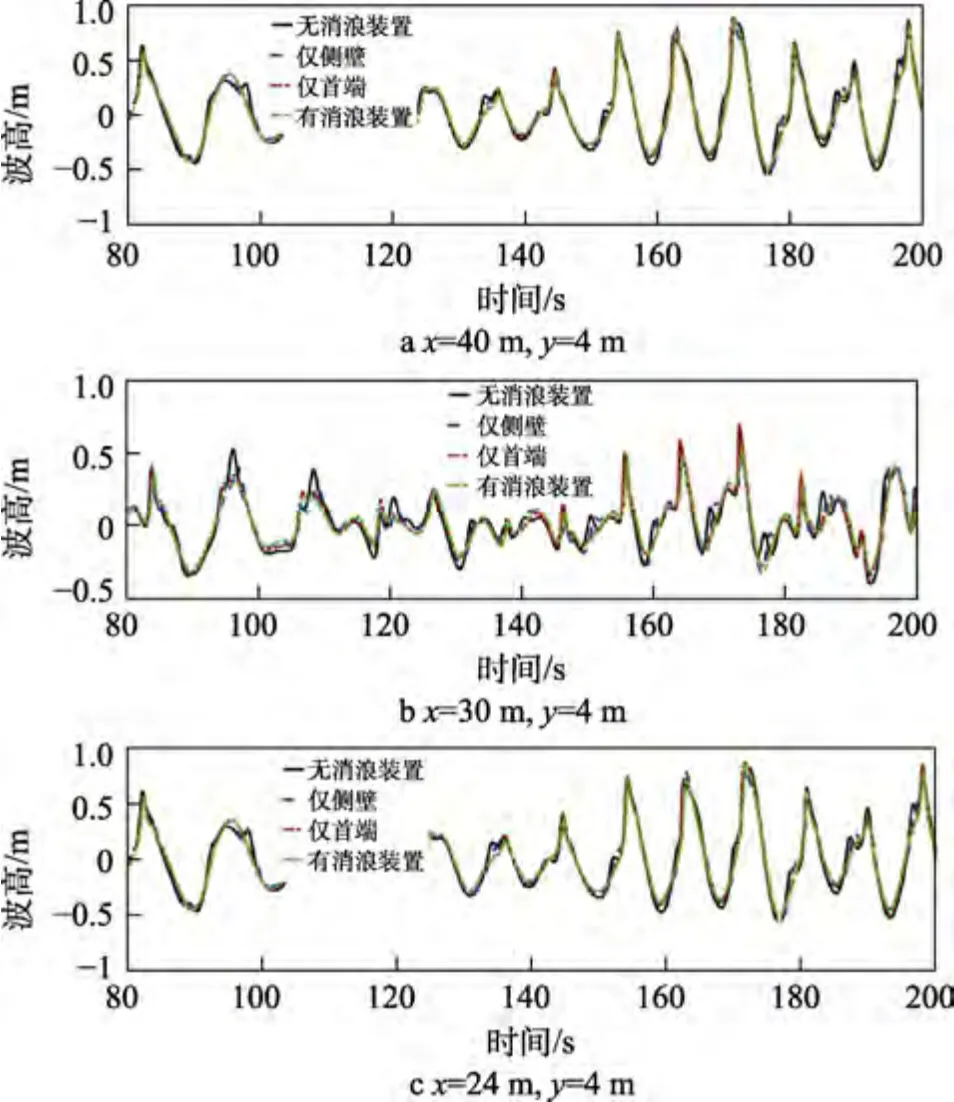
圖16 艙內波面時程曲線對比Fig.16 Comparison of wave surface time history curves in cabin
此外,本文還定量地對消浪裝置的消浪性能進行了分析。本文計算了每一個監測點的波浪曲線的能量,每種工況對所有監測點的能量求和,作為評定該工況下艙內波面能量的指標。之后,分別使用方案二、三、四的波面能量減去無消浪裝置的方案一的能量,并求出該差值對于方案一能量的比例,以此來定量地評定削減掉的能量,見表3。可以看出,首端與側壁消浪裝置對該波況下的波面具有不錯的消能作用,其中同時安裝了首端與側壁消浪裝置的方案消掉接近40%的波面能量,這將為艙內的設備物資安全工作提供重要保障。
從表4 可以看出,本文給出的具有首端和側壁消浪裝置的方案四相較于沒有消浪裝置的空艙情況在多種不同的波況中,全部都可以消掉40%左右的波面能量。這將使船舶尾艙內的波面更加平穩,作業更加安全。事實上,由于塢艙尾端開口處的波浪幾乎沒有受到消浪裝置的作用,消浪效果均發生在艙內的部分,因此如果只將艙中線內部的監測點的波面能量作為參考指標,消浪效果將會更好。基于此,本文選取艙內橫坐標x=26 m 到x=48 m 的部分進行能量求和,得到結果見表5。
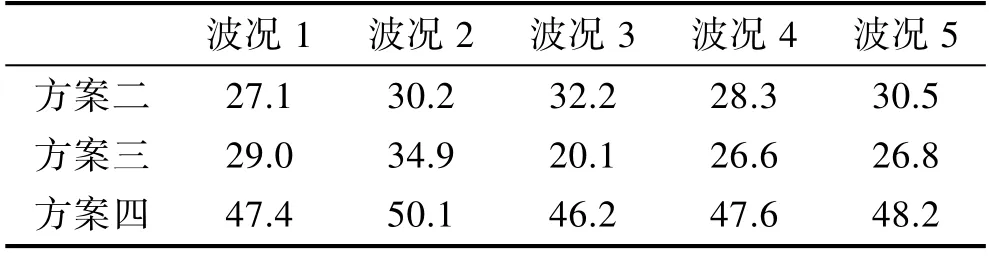
表5 艙中線以內不同波況下3 種方案相較于空艙削減掉的波浪能量Tab.5 Wave energy reduced by the three schemes under different wave conditions within ship centerline compared with that of the empty cabin%
從表5 可以看出,尾艙中線以內的部分消浪效果相較于整艙所有監測點的平均能量消浪性能得到了進一步的提升,能量削弱達到將近50%。這進一步說明了本文所給出的消浪裝置的主要作用發生在艙內部分,并且進一步證實了本文消浪裝置的有效性。
3 結論
1)不論是同時裝有首端和側壁消浪裝置,還是僅裝有一種消浪裝置,船舶的響應情況均與無消浪裝置的工況幾乎沒有差別,也即消浪裝置的裝載對船舶的響應情況幾乎沒有影響。
2)本文提出的帶有首端和側壁消浪裝置的消浪方案對不同情形的入射波引起的艙內波浪均具有不錯的消浪性能。其中,同時裝有首端和側壁消浪裝置的情況消浪性能要優于僅有1 種消浪裝置的情況,消浪效果達到40%~50%。
3)本文提出的消浪裝置方案對艙內波浪的消減主要在首端附近至艙中段的區域效果較為明顯,在遠離首端的塢艙尾端開口區域效果不明顯,并且對波高較高的波浪消浪效果要更加明顯。

