基于改進的動態多種群粒子群優化算法的配電網重構

袁 昕，劉明紅，王鵬朝，李 清

（國網新疆電力有限公司經濟技術研究院，新疆 烏魯木齊）

引言

配電網重構是確定配電網開關的狀態，使線路損耗在諸如饋線容量、電壓降和變壓器容量等條件的約束下得到最大優化。由于候選開關組合很多，并且每個開關狀態都是離散的，所以配電網絡重構被認為是一個離散的、非線性約束的組合優化問題。文獻[1]提出了一種具有鄰域搜索機制的免疫算法用于配電網重構；文獻[2]結合進化過程中的自適應參數變化，提出了具有個體老化機制的遺傳算法，從而避免了早熟收斂；文獻[3]采用循環編碼的遺傳優化與免疫方法相結合，以減少不可行解的產生。

粒子群優化（PSO）是由Kennedy 和Eberhart 于1995 年提出的一種簡單而有效的啟發式優化算法[4]。雖然粒子群算法在連續問題中得到了廣泛的應用，但它并沒有很好的解決離散組合問題，如配電網重構。考慮到電源的輸出，文獻[5]采用二進制PSO（BPSO）解決重構問題，粒子位置的每個維度表示開關的狀態，即，0 表示打開，1 表示關閉。

本文提出了一個基于更新策略，結合動態多種群的改進粒子群優化算法（DMS-PSO），相對于傳統粒子群算法有著更好的魯棒性能和收斂精度，更加適合于解決離散組合問題。

1 基于集合更新策略的動態多種群粒子群優化算法（DMS-PSO）

1.1 動態多種群粒子群算法

DMS-PSO 算法是一種全局優化算法，整個群體分成幾個亞組以相互協調，且在進化的大多數時間，進化信息不會在不同的子組之間交換。在幾次迭代之后，整個群體將被重組，相互交換進化信息，這樣就可以有效地擴展整個群體的搜索空間，提高收斂精度。算法的搜索過程如圖1 所示。

圖1 DMS-PSO 搜索過程

從圖1 中，我們可以看到粒子的搜索空間主要通過重組操作擴展，更新規則如下：

1.2 基于集合概念的速度和位置更新機制

重新定義速度和位置變量并更新機制解決離散化，具體內容表示如下：

（1） 速度變量定義為具有可能性的集合。

式中：vid為粒子在n 維度上的速度；Ed為表示第n 維中的所有元素的明確集合；ed是Ed中的某個元素；p（ed）為ed 的概率。

（2） 當初始化粒子速度時，選擇維度中的所有元素，并為每個元素分配隨機可能性，即p（ed）。

（3） 對于速度更新機制，原始公式沒有任何變化，而公式中的計算運算符不同。系數c 和速度集合vid之間的乘法運算符被定義為系數c 和速度元素中的可能性p（ed）之間的乘法。如果可能性大于1，它將被限制為1。

兩個清晰的集合之間的負算子被定義為元素的加法。速度集合A 中的元素（A 和B 都具有）將從集合A 中移除。這里A 和B 表示兩個速度集。

具有可能性的兩個集合V1，V2之間的加運算符被定義為元素加法。對于元素e 兩個集合，具有更大的可能性將被保持。

（4） 在更新粒子位置時，產生隨機可能性?，并且將選擇具有大于?的可能性的元素以形成候選集candi?。

隨機選擇候選集中的元素并參與位置更新以形成新的粒子位置。如果沒有可能大于隨機數?的元素，則候選集將為空，并且該維中的位置變量不會改變。

1.3 考慮鄰域搜索的動態多種群粒子群算法

為了進一步提高算法的利用能力，本文提出了一種鄰域搜索機制。這種機制給予粒子一定的可能性Pc以彼此交換信息，其可能性預先確定為指數函數分布。主要步驟如下所示：

（1） 首先，對于第i 個粒子的第d 維，生成隨機可能性rand。如果rand 大于第i 個粒子的預定可能性Pc（i），則ith的位置X（i，d）不改變，否則到達步驟（2）。

（2） 其次，在整個群體ps 中隨機選擇兩個粒子Rnd1、Rnd2，并且將具有更好最佳適應度Fit[pbest（Rnd）]的粒子以更新X（d）。

（3） 最后，如果d 大于最大尺寸數D，程序結束，否則d=d+1，繼續步驟（1）。

2 拓撲的簡化和編碼

由于分布網絡必須滿足網絡的徑向性質，當應用智能算法來解決分布網絡重新配置問題時，會產生大量不可行解，有必要簡化拓撲約束判斷的過程。本文采用等價分支的簡化方法。閉合所有開關，選擇度數大于2 的節點和互連開關的端點為關鍵節點。關鍵節點之間的分支是等價的分支，在拓撲約束的判斷中起到相同的作用。如上所述，PG＆E 69 節點分布系統可以簡化為圖2。

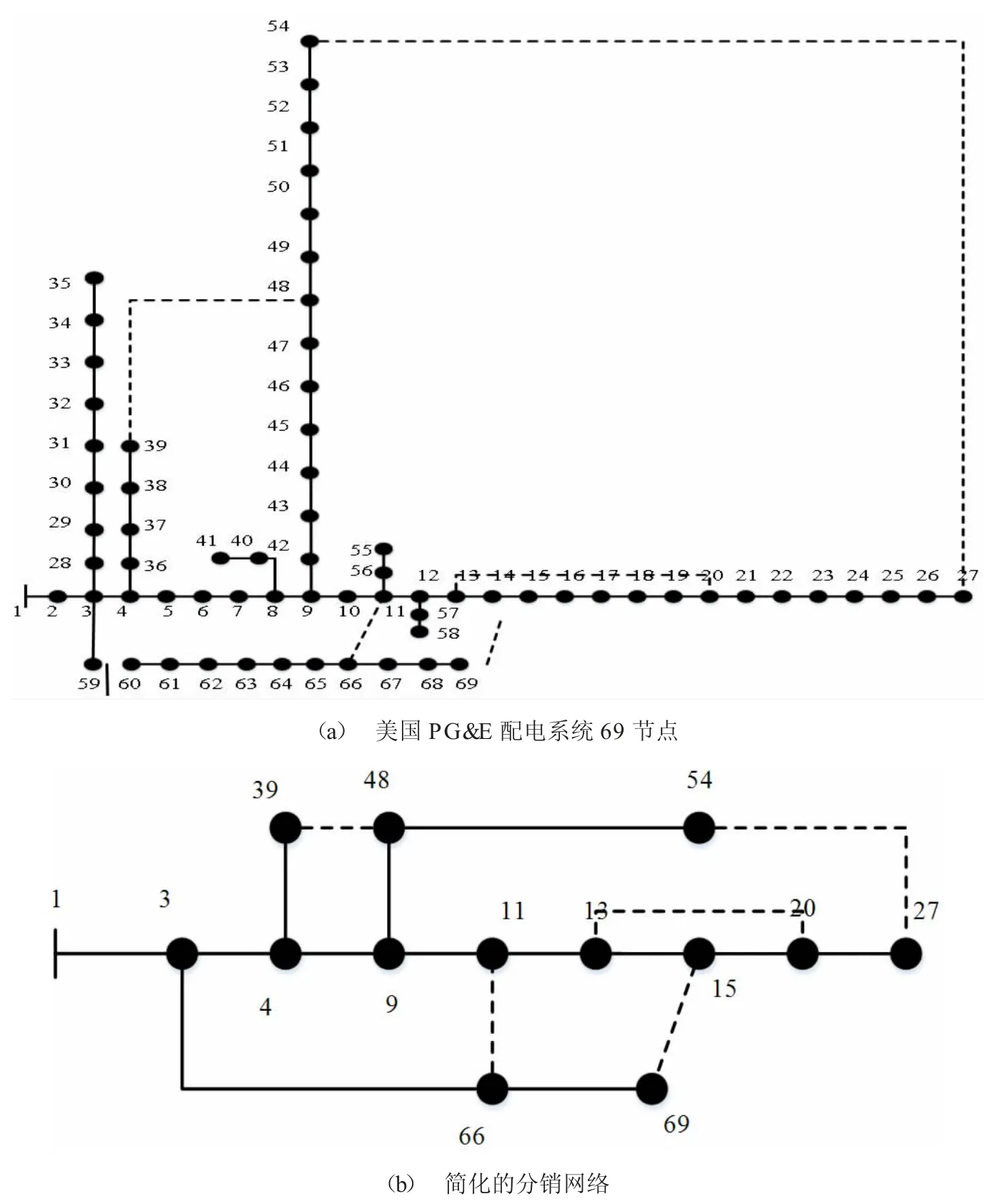
圖2 PG＆E 69 節點分布網絡簡化的過程

對于編碼方法，采用循環編碼方法，其中每個循環中只能選擇一個開關。對于圖論中的樹的概念，連接圖中的輻射樹需要打開和關閉相等數量的開關以轉換成另一輻射樹拓撲。循環編碼方法可以完美地滿足這些要求并有效地壓縮解空間。例如，69 節點系統原始解空間為273=1057，而循環編碼可以將解空間壓縮約為106。

3 不可行解的修復機制

對于不可行解，傳統的方法是重新求解，不僅低效而且更重要的是影響收斂精度。為了進一步提高算法的運行效率，提出了一種修復拓撲不可行解的方法。對于不同類型的不可行解，根據各自的特點進行判斷，并進行相應的修復。由于簡化和編碼方法，不可行解可以分為兩類：回路或者“孤島”。對于第一種情況下，回路的開關對應的可用于區分類型的解，關閉一個重復的開關將有效地解決這些解；于另一種情況下，關閉所有的在循環中的接觸開關可以有效地解決不可行解。

4 實驗結果與討論

為了驗證算法的有效性，基于PG&E 69 節點分布式系統，分布式發電機安裝在21,50,39 節點上，具體參數見表1。

表1 DG 的位置和能力

對于參數選擇，種群大小設置為81，最大迭代為50，子組大小為3，慣性常數為0.9 至0.4，較大的慣性權重保證迭代初期有較大的全局搜索能力，迭代后期較小的慣性權重有利于更精確的局部搜索。

在配電網的69 節點上對所提出的修復機制進行測試。系統的詳細參數如圖2 所示，結果如表2 所示。通過對比我們可以看出，本文所提出的方法具有更好的求解精度。

表2 使用DG 進行配置和優化的結果

本研究方法迭代15 次就收斂，文獻[5]的方法迭代24 次收斂，驗證了本文方法具有較高的計算效率，原因是修復機制可以更好地利用不可行解中的信息，從而加速收斂過程，提高了計算效率。

5 結論

提出了一種基于改進的動態多群粒子群優化（DMS-PSO）的配電網重構方法。針對粒子速度和位置提出了基于集的更新策略，提出了鄰域的學習策略來提高算法的局部搜索能力和一種修復機制，以提高算法的收斂速度和準確性，在69 節點配電網絡系統的測試結果表明所提出的方法具有良好的性能。