基于容積粒子濾波的配電網動態狀態估計

石倩,劉敏

(貴州大學 電氣工程學院,貴陽 550025)

0 引 言

為解決經濟發展與環境惡化間的矛盾,分布式電源(DG)逐漸接入配電網[1],導致配電網運行和控制方式復雜化。作為配電管理系統核心的狀態估計可以準確感知系統的運行狀態,為其他高級應用軟件提供數據。因此提高配電網動態狀態估計的精度對系統安全穩定運行至關重要。

容積卡爾曼濾波等基于卡爾曼框架的濾波算法雖被廣泛應用于配電網狀態估計,卻對強非線性非高斯系統濾波精度有限,而基于貝葉斯估計的PF本質是利用空間一組帶權值的粒子分布來近似概率密度函數,能夠表示任何一種概率分布,對任意非線性、非高斯系統都具有良好的濾波能力。鑒于傳統PF的重要性密度函數為狀態轉移概率函數[2],沒有考慮最新的量測信息,粒子易出現退化現象。因此學者們提出了改進算法,例如文獻[3]用擴展卡爾曼濾波[4](EKF)設計PF的重要性密度函數,形成擴展粒子濾波(EPF)算法。由于生成預測粒子的過程中融入了最新量測信息,濾波精度有所提高,但是EKF算法直接對非線性系統線性化,只保留泰勒展開式的第一項,引入了較大的截斷誤差,對于強非線性系統,濾波誤差會大幅提升。文獻[5]在EPF算法的基礎上進行改進提出了無跡粒子濾波(UPF)算法,使用無跡卡爾曼濾波[6](UKF)設計重要性密度函數。仿真結果表明:無論噪聲是高斯分布還是非高斯分布,UPF算法對電力系統的狀態估計誤差都較小。因為UKF算法采用無跡變換代替EKF算法的局部線性化,具有2階及以上的濾波精度,且文獻[7]證實了UPF算法濾波精度比EPF算法高。針對UPF算法需產生大量sigma采樣點,運行時間長,文獻[8]提出了CPF算法,仿真分析表明CPF比UPF算法濾波精度高,運行時間短。

為克服容積卡爾曼濾波算法對噪聲為高斯分布的限制和PF算法粒子易退化的問題,文中依據配電網三相不平衡的估計模型,提出了基于CPF算法的配電網動態狀態估計法,結合了CKF與PF算法的優點。利用融入了最新量測的CKF算法設計的重要性密度函數更接近真實后驗分布,提高了算法的濾波精度,且對強干擾的非線性系統具有較好的濾波能力。

1 動態狀態估計理論

狀態估計有靜態與動態兩種估計法,動態狀態估計利用冗余的量測量與系統模型(系統方程和量測方程)估計當前斷面的狀態并預測下一時刻的狀態在分布式電源高滲透率的配電網中有較好的應用前景。配電網的系統模型可以由式(1)表示:

(1)

式中xk、yk分別為系統狀態量與量測量;f(·)、h(·)分別為狀態轉移方程與量測方程,具體形式見第3節;vk表示量測噪聲;wk表示過程噪聲。

2 容積粒子濾波

2.1 粒子濾波原理

粒子濾波是一種基于蒙特卡洛(Monte Carlo)的貝葉斯(Bayes)濾波算法[9]。核心思想是在Bayes估計理論下,利用量測量對未知變量的先驗分布進行修正得到后驗分布,即:

(2)

式中p(y1:k|x0:k)表示系統量測量為y1:k的似然概率密度;p(x0:k)為系統先驗概率密度。

粒子濾波算法大致可概括為以下幾個步驟:

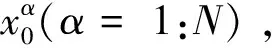
(2)權值更新。通過不斷更新的量測量來改變粒子的權值,針對Bayes重要性采樣存在計算量大和占用空間大的問題,在Bayes重要性采樣基礎上引入序貫重要性采樣,用遞歸的形式更新粒子權值:

(3)

由于傳統PF算法的重要性密度函數為狀態轉移函數:q(xk|x0:k-1,y1:k)=p(xk|xk-1),沒有計及最新量測信息的影響,所以需進一步研究更合適的重要性密度函數;

(3)重采樣。對粒子做進一步處理,復制大權值的粒子,淘汰小權值的粒子,重新得到一組等權值的粒子集,能更好地近似隨機變量的后驗分布;

(4)狀態估計。基于重采樣得到的隨機粒子集,依據蒙特卡洛原理,用樣本均值代替復雜的積分運算,得到變量的最優估計值。

2.2 容積粒子濾波基本原理

傳統PF算法的優點在于不限制噪聲的類型,對非線性非高斯系統有較強的濾波能力,缺點在于重要性密度函數沒有考慮最新量測信息的影響,過分依賴系統模型。在模型不準確的情況下,隨著算法的迭代,粒子逐漸退化,故粒子集與真實的后驗分布間的誤差逐步增大。

鑒于容積卡爾曼濾波算法精度高、數值穩定性佳等優點,文中在PF的基礎上引入CKF形成容積粒子濾波算法。CPF利用CKF算法計算的狀態量均值和方差作為建議分布函數,并用此函數來代替傳統PF的重要性密度函數生成預測粒子。故在每一次更新粒子時都使用了最新量測信息,采樣得到的粒子能準確描述真實的后驗分布。CPF既保留了CKF對非線性系統優良的濾波能力,又保留了PF算法的靈活性和強抗干擾性能力,所以不受系統類型的限制。理論上,濾波精度可以隨采樣粒子的增加而無限提高,靈活性強。且生成粒子階段還采用了重采樣技術,通過優勝劣汰的策略進一步提高估計精度。

2.3 CPF算法步驟

CPF與PF的區別在于:CPF利用CKF的估計結果替代PF的重要性密度函數。具體濾波過程如下:

(2)重要性采樣。利用CKF計算每個粒子的均值和方差(m=2n,n為狀態量維數,m為容積點數):

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

④計算采樣并更新粒子。由CKF算法為PF設計的重要性密度分布為:

(16)

(17)

(18)

(19)

(3)重采樣。隨著迭代次數增加,粒子退化現象逐漸加重,此時有效粒子數為:

(20)

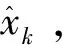
(21)

3 基于CPF的配電網動態狀態估計

配電網中分布式能源的高滲透率已經導致傳統配電網向多能供電的主動配電網發展,配電網結構已發生巨大的變化。文中提出了基于CPF的配電網狀態估計模型,利用CPF算法對配電網運行狀態進行實時感知。該算法既克服了容積卡爾曼濾波受限于噪聲為高斯分布的問題,又保留了PF算法較強的抗干擾能力。

鑒于配電網分支多,且三相不對稱的特點,故不能仿照輸電網任選其中一項進行分析,需要建立配電網的三相不對稱模型。選擇配電網的節點電壓幅值和相角作為狀態變量,故式(1)配電網系統模型中的狀態變量可表示為x=[Vφ,θφ],其中φ表示配電網的A、B、C三相。對于狀態轉移函數f(·),文中利用兩參數指數平滑法[10]來近似計算:

(22)

式中s與b為平滑參數,在0～1之間取值;xk|k為k時刻的狀態估計值;xk+1|k為k+1時刻的預測值。

量測量主要有支路功率和節點功率、支路電流與電壓幅值,因此配電網三相狀態變量(x)與量測函數(h(·))間的關系式[11]如式(23):

(23)

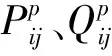
4 仿真結果分析

用IEEE 33節點系統[12]來測試算法的有效性,具體網絡參數詳見文獻[13],其中分布式電源(DG)由節點6、18接入系統中。文獻[14]通過兩種算法的組合預測法計算出分布式電源出力的預測誤差可達到5%以內。鑒于DG的接入加強了對系統的干擾,故文中把DG等效成PQ節點,把DG出力作為偽量測加入配電網狀態估計中。

為利于驗證文中所提算法的有效性,把配電網潮流計算得到的電壓幅值和相角作為本次實驗對比的真值。在真值基礎上疊加隨機誤差作為量測數據輸入文中所提狀態估計器中,CPF算法中配電網各節點狀態變量的初值設為系統初始時刻的真值。由于分布式電源的不斷滲透,導致配電網運行方式復雜化,傳統的量測裝置已不能滿足狀態估計對配電網運行狀態的準確跟蹤。故文中采用PMU與SCADA混合量測模式,在真值基礎上,SCADA系統疊加均值為0,標準差為0.02的隨機誤差,PMU系統疊加均值為0,標準差為0.001的隨機誤差。鑒于SCADA的采樣周期比PMU長,規定在SCADA采集數據時,PMU的量測數據才能使用。引入電壓幅值的相對誤差與電壓相角的絕對誤差作為濾波性能指標,直觀分析不同算法的濾波效果:

(24)

式中Nbus為配電網總節點數;θie(k)和Uie(k)分別為k時刻電壓幅值和相角的估計值;θit(k)和Uit(k) 分別為k時刻電壓幅值和相角的真實值。

4.1 基本測試結果分析

在含分布式電源的配電網中使用CPF算法進行狀態估計,進行50次模擬仿真,每次模擬CPF取100個粒子,任意取節點6進行仿真分析,節點6的C相電壓幅值和相角真值與CKF、CPF算法濾波結果間的對比如圖1所示。

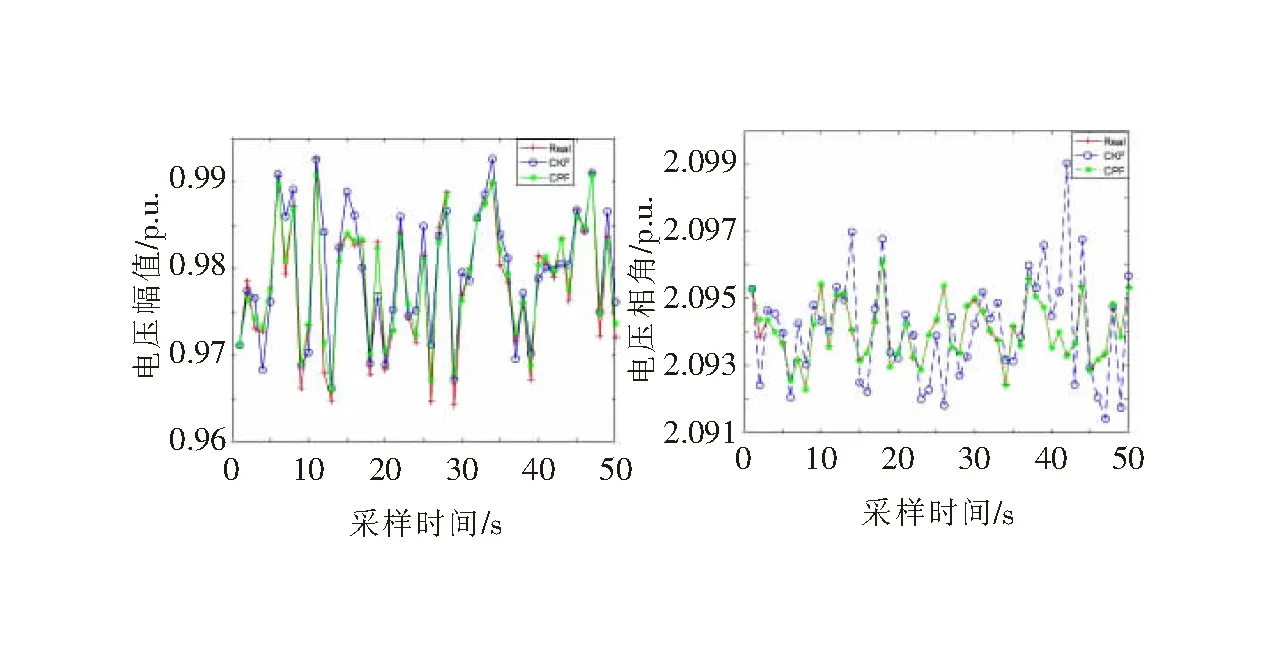
圖1 狀態估計結果對比

由圖1可知,DG的接入導致配電網節點電壓幅值和相角出現明顯波動。因為隨著DG的不斷接入,系統過程噪聲增大,干擾因素較無源系統增多。CPF結合了CKF算法對非線性系統良好的處理能力和PF算法的強抗干擾能力。故在狀態估計啟動后,CPF算法能準確跟蹤配電網的運行狀態,對電壓幅值和相角的濾波精度比CKF算法高。為了更直觀的分析不同算法的濾波效果,CKF和CPF算法的電壓幅值相對誤差與電壓相角絕對誤差的平均值和最大值如表1所示,兩種算法濾波性能指標對比結果如圖2所示。

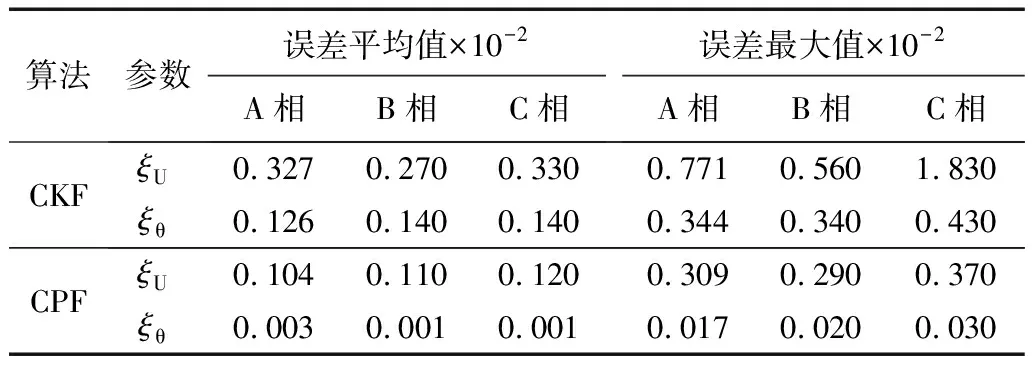
表1 不同算法的狀態估計指標

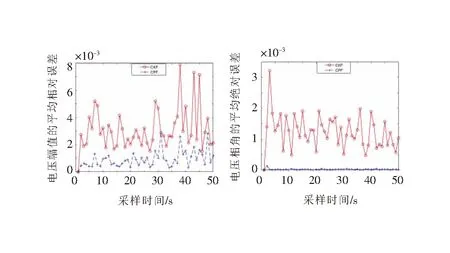
圖2 電壓幅值和相角的誤差

由圖2和表1可以直觀看出,在性能指標的平均值和最大值上CPF算法濾波效果優于CKF算法。CPF算法濾波結果誤差更小,在干擾噪聲下能夠準確估計系統運行狀態,確保系統安全穩定運行。

4.2 不同粒子數測試結果分析

為研究不同采樣粒子數對CPF算法濾波結果的影響,在IEEE33節點系統中進行測試。其他參數保持不變,僅改變采樣粒子數,利用文中算法對配電網各節點的運行狀態進行濾波。 A、B、C三相濾波性能指標的平均值與最大值的仿真結果如表2所示。

表2 不同粒子數下的性能指標

由表2可知,CPF濾波精度隨粒子數增加而提高,單步耗時卻基本不變,故可以通過選擇采樣粒子數來達到理想的濾波精度,表明CPF算法任保留著PF算法的靈活性。比較表2和表1可知,當CPF算法粒子數為30時濾波精度也比CKF算法(單步耗時為0.55 s)高。所以相較于CKF算法,CPF算法能夠在相同的單步耗時情況下達到更高的濾波精度。

4.3 非高斯噪聲下測試結果分析

對于配電網的動態狀態估計,基本都是假設量測噪聲服從高斯分布。而對于實際配電網,高滲透率的分布式能源加強了對系統的干擾,導致量測噪聲增大甚至為非高斯噪聲。

為了驗證文中所提算法在非高斯量測噪聲存在時有良好的濾波效果,在IEEE 33節點系統中進行測試,分布式電源的量測噪聲設置為服從分布參數為2.06和2.5的貝塔分布。利用CPF算法對配電網運行狀態進行濾波,每次模擬仿真CPF取100個粒子,任意取節點6進行仿真分析,節點6的C相電壓幅值和電壓相角真值與CKF、CPF算法濾波結果間的對比如圖3所示。

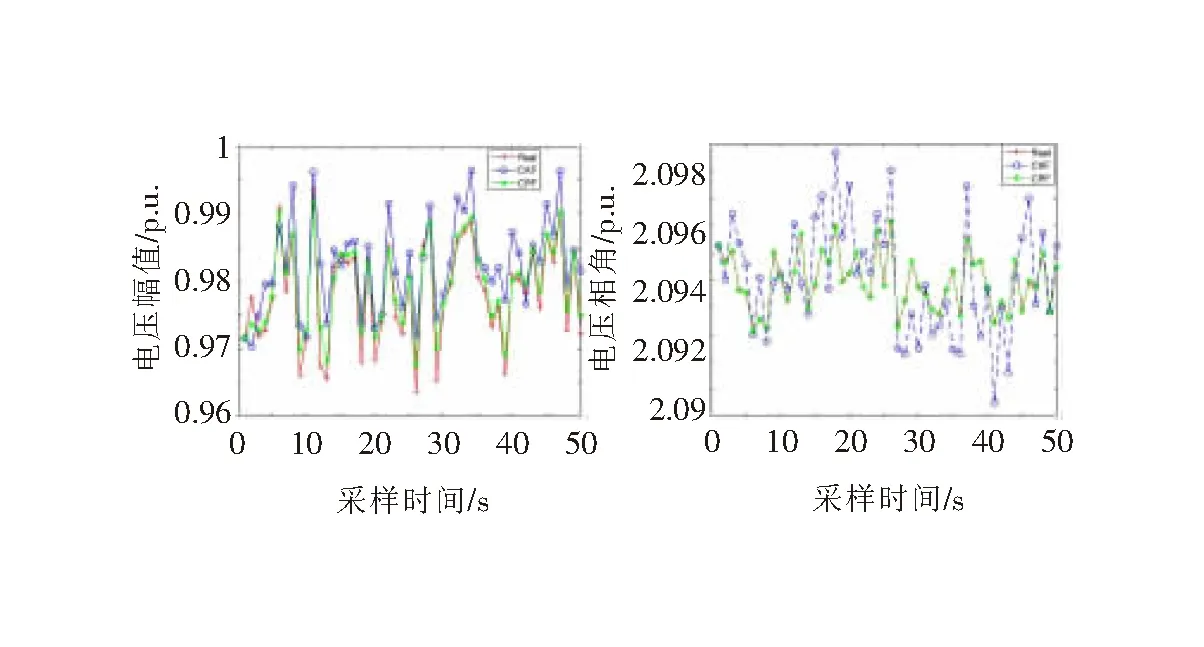
圖3 非高斯噪聲下狀態估計結果

由圖3可知,當存在非高斯的量測噪聲時,CPF算法任能準確跟蹤電壓幅值與相角的真值,CKF算法的濾波性能卻大大降低,因為基于卡爾曼框架的濾波算法對于非高斯系統的濾波能力有限。而基于PF框架的CPF保留了傳統PF對非高斯系統良好的濾波能力,同時利用CKF算法設計PF算法的重要性密度函數,克服了PF粒子易退化的缺點。為了量化兩種算法在非高斯量測噪聲下的濾波性能,表3給出了CPF與CKF算法電壓幅值相對誤差和電壓相角絕對誤差的平均值和最大值。

表3 非高斯噪聲下性能指標

由表3可知,存在非高斯的量測噪聲時,CPF比CKF算法的濾波誤差更小,比較表3和表1可知,與高斯分布相比,兩種算法對于電壓幅值的濾波誤差都有所增加;對于電壓相角來看,CPF算法濾波精度幾乎沒變,而CKF算法濾波精度卻大幅降低。總體來看,無論量測噪聲為高斯還是非高斯分布,CPF算法比CKF算法的濾波精度更高。

5 結束語

文中提出了基于CPF算法的配電網動態狀態估計模型。仿真結果表明,CPF算法既保留了CKF算法對非線性系統良好的處理能力又保留了PF算法的強抗干擾性能力,相比CKF算法能更好地處理DG并網帶來的干擾。且CPF算法可以通過調整采樣粒子數改變濾波精度,較CKF算法更靈活。最后,對于存在非高斯量測噪聲的情況,CPF算法比CKF算法具有更高的估計精度。