考慮圍巖孔隙特性的深部巷道注漿加固數(shù)值方法研究

文旭東 盧海峰,2 劉泉聲,2 劉 濱 吳月秀,2

(1.武漢大學(xué)土木建筑工程學(xué)院,湖北 武漢 430072;2.巖土與結(jié)構(gòu)工程安全湖北省重點實驗室,湖北 武漢 430072;3.中國科學(xué)院武漢巖土力學(xué)研究所,湖北 武漢 430071;4.巖石力學(xué)與工程國家重點實驗室,湖北 武漢 430071)

注漿技術(shù)是一項實用性強、應(yīng)用廣泛的工程技術(shù),是改善巖土體物理力學(xué)性質(zhì),封堵地下水的有效措施,是解決煤礦深部高應(yīng)力環(huán)境下泥巖巷道支護難題的必要措施[1-2]。淮南礦區(qū)是國家大型煤炭基地中的兩淮基地之一,埋藏深度2 000 m 以上的煤炭資源量約500×108t,該區(qū)域由于地質(zhì)構(gòu)造和沉積歷史,巷道圍巖中泥巖或泥質(zhì)膠結(jié)的巖石十分常見,整個礦區(qū)-800～-1 000 m 深度范圍內(nèi)約70%的巖石巷道圍巖為泥巖或泥質(zhì)膠結(jié)的巖石。一方面泥巖本身物理力學(xué)性質(zhì)特殊,遇水極易軟化,強度降低;另一方面,巷道圍巖處于深部高應(yīng)力環(huán)境,巖體結(jié)構(gòu)復(fù)雜,裂隙水發(fā)育,因而巷道在開挖掘進過程中很難保持穩(wěn)定,極易發(fā)生變形破壞,必須采取有效的支護加固措施,才能保證巷道圍巖穩(wěn)定和礦區(qū)安全開采。

有關(guān)注漿加固的研究,國內(nèi)外學(xué)者開展了許多卓有成效的工作。在漿液擴散規(guī)律和理論模型方面,GROPPO 等[3]進行了單裂隙中漿液流動過程模擬試驗,研究了漿液壓力、流速等對漿液擴散半徑的影響,劉嘉材[4]、石達明[5]推導(dǎo)出了擴散半徑與注漿時間的表達式,郝哲等[6]、阮文軍[7]推導(dǎo)了基于賓漢姆流體的漿液擴散方程,但大多數(shù)漿液在裂隙內(nèi)滲流的理論都會對圍巖裂隙進行簡化,難以反映漿液的真實擴散情況。近年來,不少學(xué)者從注漿試驗方面進行了探究,韓曉雷等[8]采用化學(xué)注漿方式對含泥粉細砂層進行注漿試驗,探究了各種因素對注漿效果的影響;楊坪等[9]建立了不同粒徑飽和砂礫石的注漿模型,研究了不同漿液及不同注漿壓力下的漿液擴散固化機制。在注漿固結(jié)體力學(xué)特性方面,張農(nóng)等[10]、劉泉聲等[11]研究了注漿固結(jié)后破裂巖塊殘余強度的變化情況;王漢鵬等[12]開展了峰后注漿加固試件的力學(xué)特性研究;李劍等[13]、饒梟宇等[14]研究了不同配比下注漿體的物理力學(xué)性能;何真等[15]在亞微觀尺度上描述了水泥石的微結(jié)構(gòu),歸納了水泥石微結(jié)構(gòu)與強度的關(guān)系;詹金武等[16]、王志等[17]通過循環(huán)沖擊試驗研究了注漿固結(jié)體的動態(tài)特性。隨著數(shù)值軟件的不斷更新,不少學(xué)者利用ANSYS、ABAQUS、COMSOL、FLAC 等軟件,模擬了注漿過程中漿液擴散規(guī)律及注漿加固效果。李慎剛等[18]應(yīng)用FLAC3D模擬了漿液在土體中的滲流過程,研究了注漿后隧道及圍巖體開挖時的應(yīng)力分布規(guī)律以及地表沉降情況;林元俊等[19]利用COMSOL 軟件建立了軟巖巷道注漿擴散瞬態(tài)計算模型和加固圈形成后的變形計算模型,對軟巖巷道滲流場和位移場進行了數(shù)值模擬研究;劉浩等[20]利用FLAC3D軟件模擬了注漿前后圍巖未開采和開采時頂?shù)装宓奈灰屏亢退苄云茐那闆r。

現(xiàn)有的研究大多數(shù)集中漿液的擴散規(guī)律及注漿前后巖體力學(xué)特性的變化,對整體注漿效果的評價方法相對較少。本研究以淮南礦區(qū)顧北煤礦泥巖巷道注漿加固工程為例,通過注漿固結(jié)體微觀結(jié)構(gòu)掃描電鏡試驗和力學(xué)特性試驗研究,對圍巖孔隙特性與注漿固結(jié)體力學(xué)特性的關(guān)系進行研究,在此基礎(chǔ)上對固結(jié)體的摩爾-庫倫本構(gòu)模型進行修正,并基于FLAC3D軟件,開發(fā)考慮圍巖孔隙特性的注漿加固評價的數(shù)值仿真分析方法,對礦區(qū)巷道群注漿加固效果進行分析計算。

1 注漿固結(jié)體力學(xué)特性試驗研究

1.1 試樣制備

試驗選取淮南礦區(qū)顧北煤礦-648 m 水平巷道泥巖,通過碎石機將其破碎成粒徑約1 cm 的碎塊,按照一定的漿液水灰比及碎石配合比澆入4 個30 cm×15 cm×15 cm(長×寬×高)的長方體模具,養(yǎng)護1 周后,通過鉆孔取芯制備成4 組不同孔隙率的圓柱形標準試樣(圖1),試樣參數(shù)取值見表1。

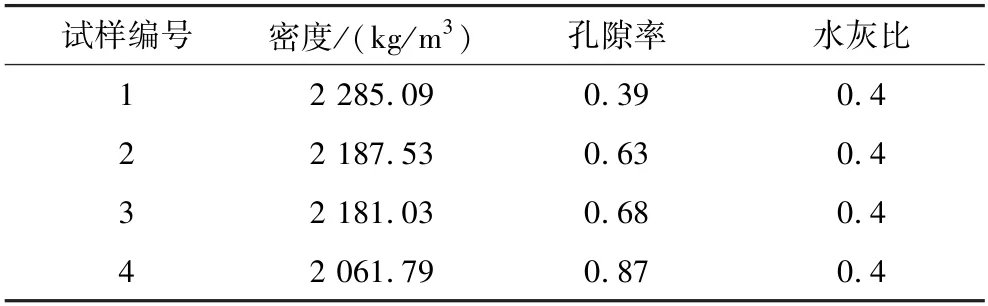
表1 試樣參數(shù)Table 1 Specimen parameters

圖1 試樣制備Fig.1 Specimen preparation

1.2 試驗過程

試驗在中國科學(xué)院武漢巖土力學(xué)研究所研制的RMT-150C 試驗機上進行(圖2),這是一種數(shù)字控制的電液伺服試驗機,是專為巖石和混凝土一類材料的力學(xué)性能試驗而設(shè)計的。

圖2 RMT-150C 試驗機Fig.2 RMT-150C test device

本研究采用RMT-150C 試驗機分別對4 組不同孔隙率的注漿固結(jié)體進行單軸壓縮試驗,所得應(yīng)力—應(yīng)變?nèi)^程曲線如圖3所示。

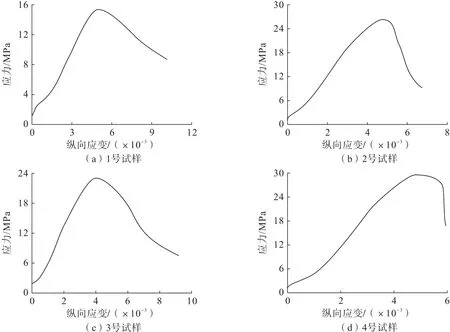
圖3 單軸壓縮應(yīng)力—應(yīng)變?nèi)^程曲線Fig.3 Complete stress-strain curves of uniaxial compression

由圖3 可知:注漿固結(jié)體與一般巖石破壞過程相似,經(jīng)歷壓密階段、彈性變形階段、塑性變形階段和破壞階段,隨著孔隙率增加,注漿固結(jié)體的彈性模量逐漸增大,單軸抗壓強度也呈增大趨勢。值得注意的是,1～3 號試樣在達到峰值應(yīng)力后還呈現(xiàn)出應(yīng)變軟化和殘余階段,孔隙率最大的4 號試樣則呈現(xiàn)出明顯的脆性破壞。

對4 組不同孔隙率試樣分別進行了不同圍壓等級下的三軸試驗,圍壓等級分別為0、2、5、10、20 MPa,試驗得到的應(yīng)力—應(yīng)變?nèi)^程曲線如圖4所示。

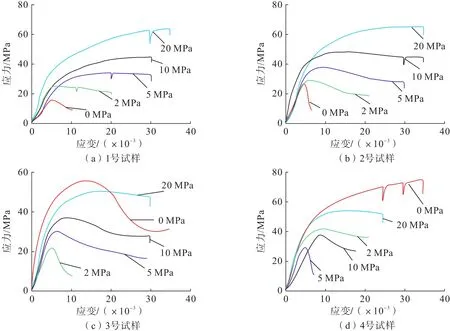
圖4 三軸壓縮應(yīng)力—應(yīng)變?nèi)^程曲線Fig.4 Complete stress-strain curves of triaxial compression

由圖4 可知:相同圍壓下,隨著孔隙率增加,注漿固結(jié)體峰值應(yīng)力逐漸增加;隨著圍壓增加,注漿固結(jié)體的殘余強度逐漸增加,且破壞模式逐漸向延性破壞轉(zhuǎn)變。

1.3 力學(xué)特性分析

1.3.1 強度特性分析

根據(jù)試驗數(shù)據(jù),分別繪制了4 組試樣的摩爾圓(圖5),得到不同孔隙率條件下注漿固結(jié)體的強度參數(shù),見表2。

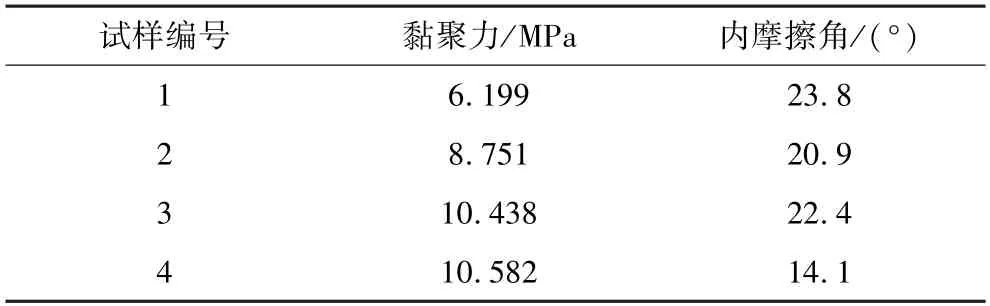
表2 注漿固結(jié)體強度參數(shù)Table 2 Strength parameters of grouting consolidation bodies

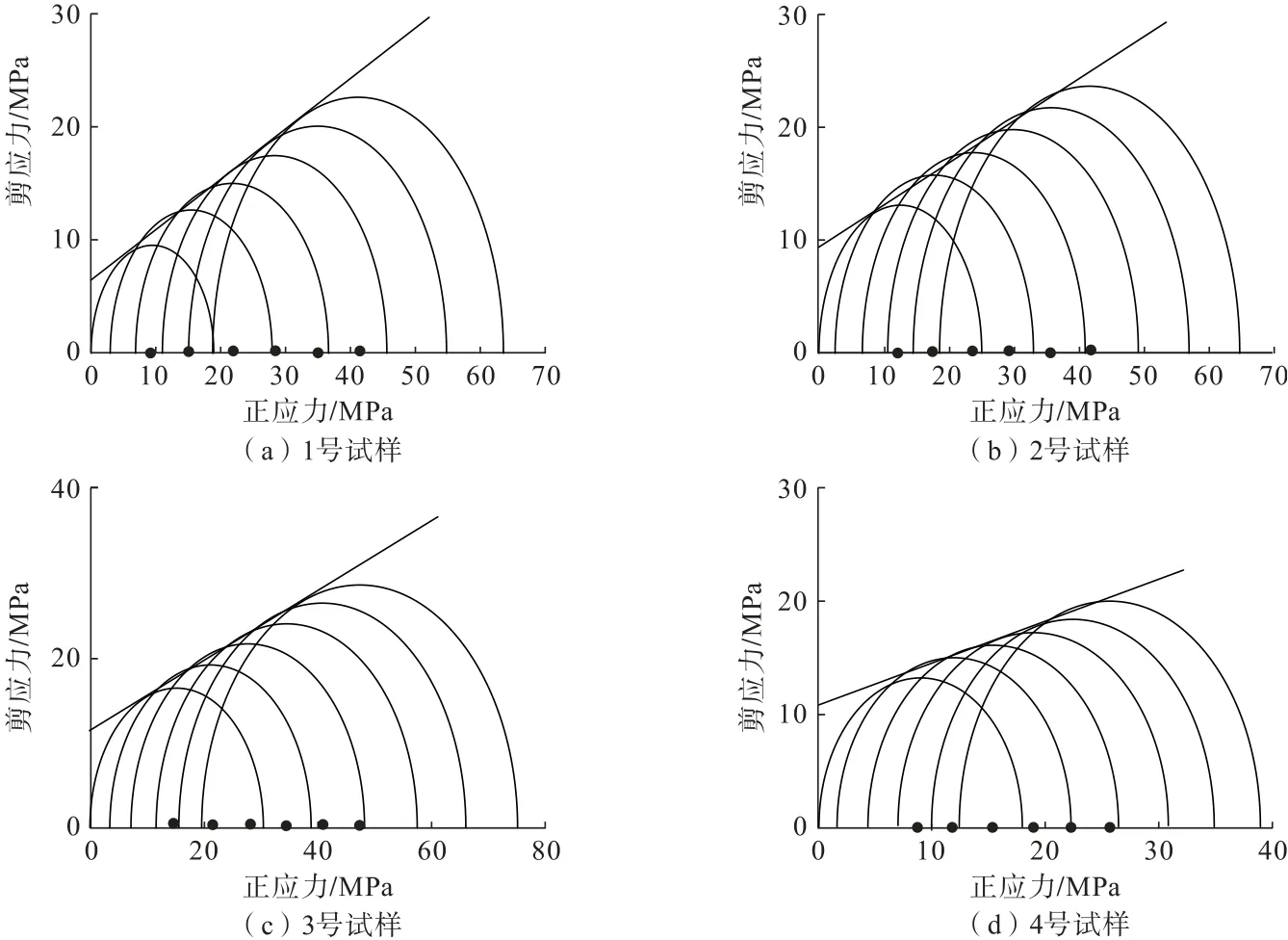
圖5 三軸試驗?zāi)枅AFig.5 Triaxial test molar circle

由表2 可知:注漿固結(jié)體的黏聚力隨著孔隙率增大呈增長趨勢,符合對數(shù)函數(shù)關(guān)系,內(nèi)摩擦角隨孔隙率增大而減小(圖6、圖7)。

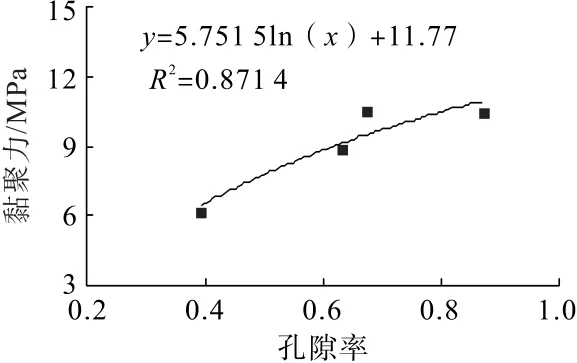
圖6 黏聚力與孔隙率的關(guān)系Fig.6 Relationship between cohesion and porosity

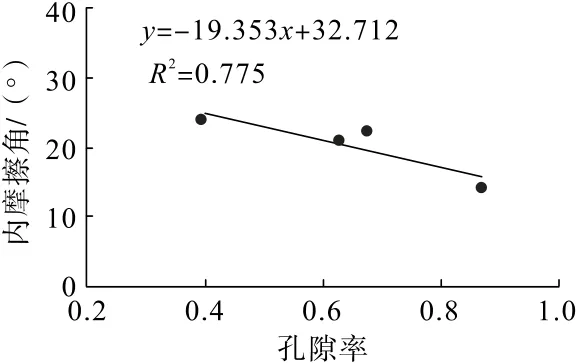
圖7 內(nèi)摩擦角與孔隙率的關(guān)系Fig.7 Relationship between internal friction angle and porosity

1.3.2 變形特性分析

孔隙率與注漿固結(jié)體彈性模量和泊松比的關(guān)系如圖8、圖9所示。由圖8、圖9 可知:彈性模量隨著孔隙率的增大呈對數(shù)函數(shù)增長,而泊松比變化規(guī)律不明顯,取值范圍為0.18～0.23。

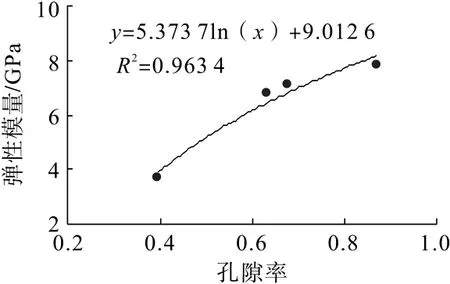
圖8 彈性模量與孔隙率的關(guān)系Fig.8 Relationship between elastic modulus and porosity

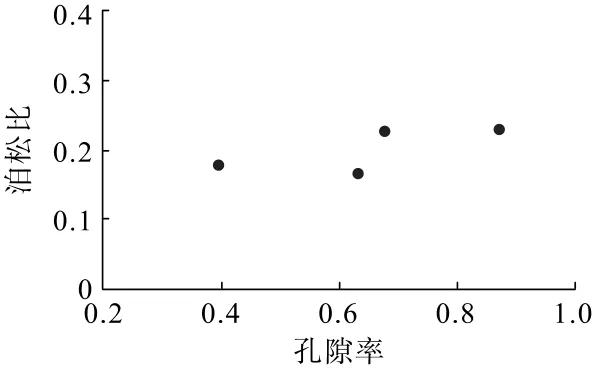
圖9 泊松比與孔隙率的關(guān)系Fig.9 Relationship between poisson′s ratio and porosity

1.4 注漿固結(jié)體膠結(jié)特性

注漿固結(jié)體的力學(xué)特性與其微觀結(jié)構(gòu)存在一定聯(lián)系,為了研究注漿固結(jié)體的微觀膠結(jié)特性,分別對4 種注漿固結(jié)體在Quanta 250 型環(huán)境電子掃描顯微鏡上進行觀察,得到了不同放大倍數(shù)下注漿固結(jié)體的微觀圖片,如圖10 至圖13所示。

圖10 1 號試樣掃描電鏡圖Fig.10 Scanning electron microscope chart of No.1 sample

圖11 2 號試樣掃描電鏡圖Fig.11 Scanning electron microscope chart of No.2 sample

圖12 3 號試樣掃描電鏡圖Fig.12 Scanning electron microscope chart of No.3 sample

圖13 4 號試樣掃描電鏡Fig.13 Scanning electron microscope chart of No.4 sample

由圖10 至圖13 可知:在較小放大倍數(shù)下,漿液與巖石接觸面接觸都很好,但隨著放大倍數(shù)增加,可以看出不同孔隙率試樣中漿液與巖石的接觸關(guān)系不同。1 號試樣孔隙率最小,通過其2 000 倍放大圖(圖10(d))可以看出,漿液與巖石之間并沒有完全解除,存在一定的微觀裂縫。隨著巖石孔隙率增加,巖塊被更多的漿液所包裹,漿液與巖石接觸面膠結(jié)越好,漿液與接觸面之間微裂隙越小,當孔隙率增大到一定程度時,漿液與接觸面互相融合,膠結(jié)效果最好(圖13)。

結(jié)合注漿固結(jié)體微觀結(jié)構(gòu)特征,可以將注漿固結(jié)體分為兩種膠結(jié)模式:一種為包裹模式,另一種為搭接模式(圖14)。包裹模式往往出現(xiàn)在巖體孔隙率較大時,漿液充填范圍較大,對巖石塊體形成包裹,這種模式下漿液與巖石塊體膠結(jié)緊密。搭接模式往往出現(xiàn)在巖體孔隙率較小時,此時漿液可充填范圍相對較小,漿液主要相鄰巖石塊體起到黏結(jié)作用,巖石塊體與漿液之間膠結(jié)相對較弱。

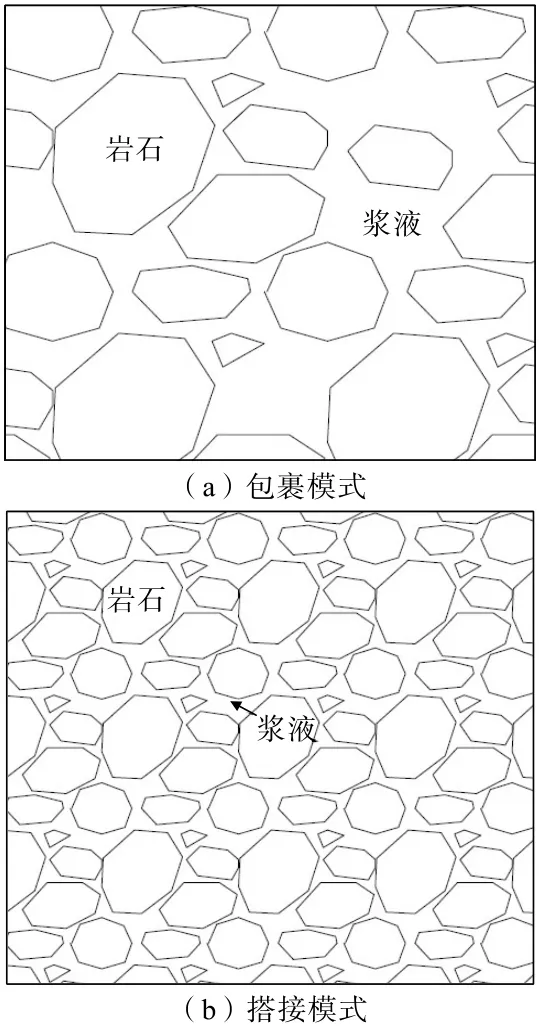
圖14 注漿固結(jié)體膠結(jié)模式Fig.14 Cementing modes of grouting consolidation body

注漿固結(jié)體的膠結(jié)模式與其力學(xué)特性有著密切聯(lián)系,包裹模式下的注漿固結(jié)體其力學(xué)特性接近水泥石的力學(xué)特性,由于漿液黏結(jié)作用強烈,使得巖體發(fā)生破壞所需的起始作用力較大,反映到力學(xué)參數(shù)上就是黏聚力較大,而搭接模式下的注漿固結(jié)體由于漿液充填相對較少,黏結(jié)作用相對較弱,所以黏聚力也相對較小。內(nèi)摩擦角大小反映了巖體發(fā)生破壞形成貫通破裂面的難易程度,在搭接模式下,由于巖石碎塊分布較多,而巖石塊體的強度相對較大,所以在破壞面形成過程中受到巖塊阻擋,形成貫通破壞面所需的力相對較大,從而使得注漿固結(jié)體內(nèi)摩擦角較大。在包裹模式下,巖塊含量相對較少,對破裂面形成路徑的阻擋影響較少,破裂面形成所需的力相對較小,使得注漿固結(jié)體的內(nèi)摩擦角相對較小。這些特性在上述固結(jié)體力學(xué)特性試驗中也很好地反映出來。

2 注漿固結(jié)體本構(gòu)模型研究

2.1 水泥石強度試驗

巖體注漿后,漿液充填裂隙或包裹碎裂塊體,一方面提高了巖體的彈性模量,影響巖體的應(yīng)力—應(yīng)變關(guān)系;另一方面對巖體強度參數(shù)產(chǎn)生影響,從而影響了巖體的屈服準則。這兩方面特性的改變使得注漿固結(jié)體的本構(gòu)模型發(fā)生改變。為了進一步研究注漿固結(jié)體與水泥石之間的強度和變形關(guān)系,依據(jù)上述注漿固結(jié)體試驗所用水灰比(表1),制備了不同齡期的圓柱形試樣,并分別進行了單軸壓縮試驗和三軸壓縮試驗,試驗結(jié)果見表3 和表4。

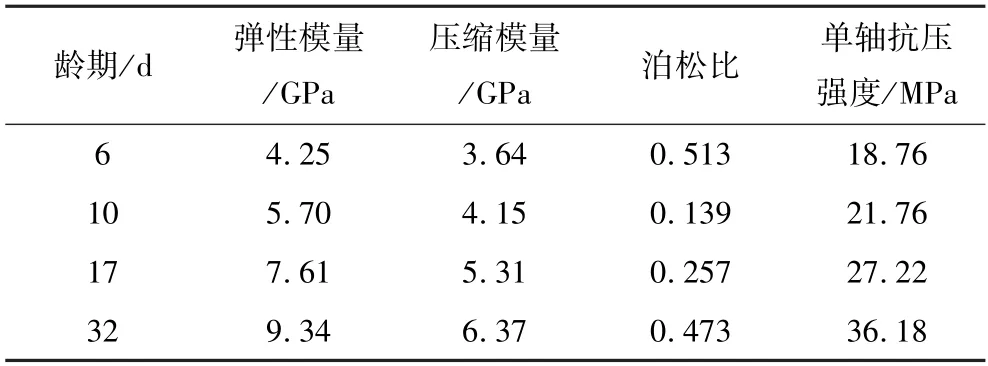
表3 單軸壓縮試驗結(jié)果Table 3 Uniaxial compression test results

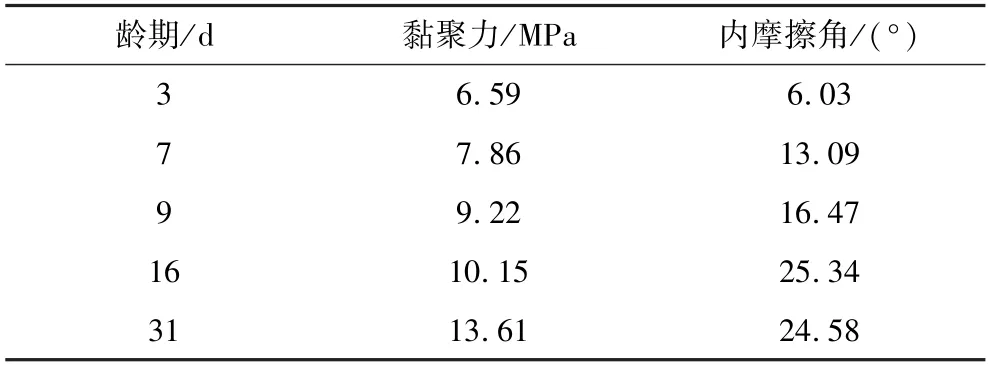
表4 三軸壓縮試驗結(jié)果Table 4 Triaxial compression test results

2.2 模量修正

式中,Eg為注漿固結(jié)體的彈性模量,GPa;β為巖體孔隙率或裂隙率;a和b為影響系數(shù)。

假定巖體裂隙或孔隙在被漿液充滿的理想狀態(tài)下,若孔隙率或裂隙率β=1 時,則式(1)中所得彈性模量實際為純漿液固結(jié)形成的水泥石的彈性模量。于是,式(1)可進一步表示為

式中,E0為水泥石的彈性模量,GPa。

由表3 可得到水泥石彈性模量和齡期之間存在以下關(guān)系:

式中,t為注漿固結(jié)時間,d;e和f為影響系數(shù)。

聯(lián)立式(2)、式(3)可以得到:

9、《關(guān)于進一步落實重點群體創(chuàng)業(yè)就業(yè)稅收政策的通知》。11月23日，為支持和促進重點群體創(chuàng)業(yè)就業(yè)，財政部、稅務(wù)總局、人力資源社會保障部財政部等三部門下發(fā)《關(guān)于進一步落實重點群體創(chuàng)業(yè)就業(yè)稅收政策的通知》（財稅〔2018〕136號），就政策落實提出具體要求。

式(4)即為修正后的注漿固結(jié)體彈性模量表達式,可見注漿固結(jié)體的彈性模量是與巖體裂隙率或孔隙率以及注漿固結(jié)時間相關(guān)的量,其影響系數(shù)a、e和f等參數(shù)取值取決于漿液性質(zhì)。

2.3 強度修正

由圖6 和圖7 得到注漿固結(jié)體的黏聚力和內(nèi)摩擦角與巖體孔隙率之間分別滿足以下關(guān)系:

式中,Cg為注漿固結(jié)體的黏聚力,MPa;φg為注漿固結(jié)體的內(nèi)摩擦角,(°);β為巖體的孔隙率或裂隙率;m、n、l和p為影響系數(shù)。

與上述模量修正類似,當孔隙率或裂隙率β=1時,所得強度參數(shù)為純漿液固結(jié)形成的水泥石強度參數(shù),即:

由表3 可知,水泥石的強度參數(shù)與齡期之間存在以下關(guān)系:

式中,t為齡期,d;h、n、k、j為影響系數(shù)。

聯(lián)立式(5)、式(6),并代入(7)可得:

式(8)即為修正后的注漿固結(jié)體強度參數(shù)表達式。

2.4 本構(gòu)模型修正

結(jié)合前文對注漿固結(jié)體模量和強度特征的研究,對巖石力學(xué)中最常用的摩爾-庫倫本構(gòu)模型進行修正,主要是對模型中模量參數(shù)和強度參數(shù)的修正。

2.4.1 修正的增量彈性定律

經(jīng)過模量修正,應(yīng)力-應(yīng)變本構(gòu)關(guān)系增量表達式可表示為

式中,參數(shù)α1、α2計算公式為

式中,β為巖石孔隙率;t為注漿固結(jié)時間,d;v為泊松比;a、e、f為影響系數(shù),由試驗確定。

2.4.2 修正的屈服函數(shù)

由Mohr-Coulomb 屈服函數(shù)破壞包絡(luò)線公式為

式中,β為內(nèi)摩擦角,(°);C為黏聚力,MPa;Nφ為材料參數(shù)。

將式(8)代入式(11)可得:

式中,m、h、n、k、p、j為影響系數(shù),可由室內(nèi)試驗獲取。

3 深部巷道群注漿加固數(shù)值仿真計算分析

通過FLAC3D軟件自定義本構(gòu)模型功能,將上述修正后的摩爾-庫倫本構(gòu)模型寫入程序,調(diào)試后以淮南礦區(qū)顧北煤礦為工程背景進行注漿固結(jié)體數(shù)值仿真計算分析。

3.1 工程概況及模型構(gòu)建

淮南礦區(qū)顧北煤礦南翼11-2 采區(qū)膠帶機巷、軌道巷和矸石膠帶機巷為3 條平行巷道(圖15),均穿越F104-1、FD104-1、F93-1 等多條斷層,受構(gòu)造帶影響,斷層附近區(qū)域圍巖破碎,裂隙發(fā)育。斷層帶寬度為25～30 m,斷層帶內(nèi)巖層破碎,巖性以泥巖為主,含少量砂質(zhì)泥巖,遇水軟化。巷道掘進先后順序為膠帶機巷、軌道巷和矸石膠帶機巷,以這3 條巷道為例,運用前面所建立的注漿固結(jié)體數(shù)值仿真分析模型,對巷道開挖過程的應(yīng)力和變形規(guī)律,以及注漿固結(jié)效果進行計算分析。

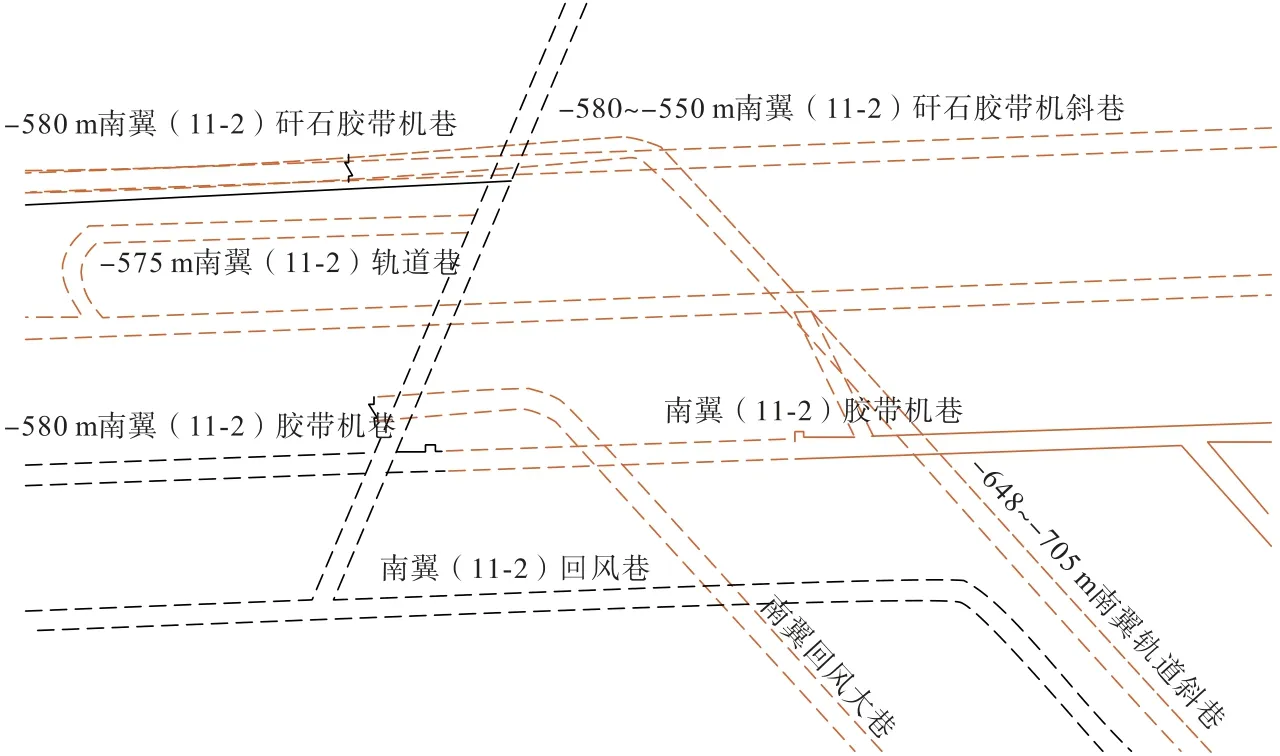
圖15 巷道平面Fig.15 Roadway plan

本研究構(gòu)建的模型長120 m、寬30 m、高60 m。模擬時采用全斷面開挖方式,開挖次序按照實際工程中巷道布置為從左到右,即膠帶機巷、軌道巷和矸石膠帶機巷。模型共有28 080 個單元,30 681 個節(jié)點,如圖16所示。

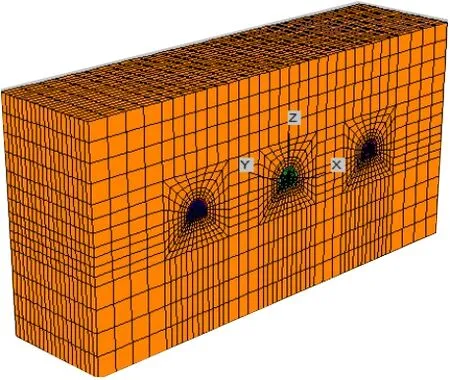
圖16 計算模型Fig.16 Calculation model

3.2 計算方案

選取本研究上述試驗中所使用的水灰比(0.4),分別進行巷道無注漿條件下的開挖過程分析以及巷道依次注漿過程分析。注漿區(qū)域劃分為3 個不同孔隙率區(qū)域,巷道外圍3 m 范圍內(nèi)巖體較破碎,采用較大孔隙率(0.5),外圍3～7 m 范圍采用0.3 的孔隙率,其他區(qū)域按原巖條件處理,注漿范圍分布如圖17所示。

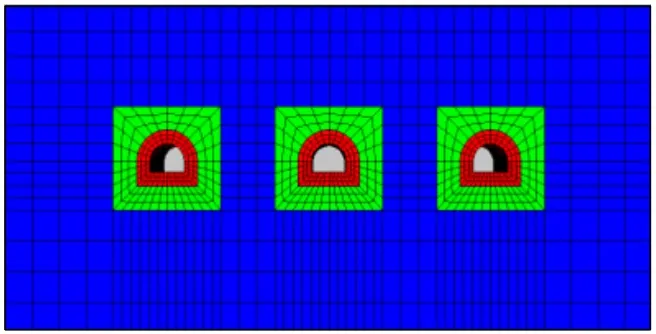
圖17 注漿加固范圍Fig.17 Scope of grouting reinforcement

3.3 無注漿條件下巷道開挖計算分析

3.3.1 應(yīng)力分布

3 條巷道應(yīng)力分布如圖18 至圖20所示。分析可知:膠帶機巷開挖后應(yīng)力調(diào)整,在巷道頂部、幫部以及底腳最大主應(yīng)力(σ1)最大,而最小主應(yīng)力(σ3)最小,兩者應(yīng)力差在頂部、幫部和底腳最大,使得巷道在頂部和兩幫易發(fā)生破壞,產(chǎn)生較大變形。巷道底部最大主應(yīng)力和最小主應(yīng)力均比其他部位小,出現(xiàn)應(yīng)力薄弱區(qū),這也是巷道易產(chǎn)生底鼓變形的主要原因;其他巷道開挖后也呈現(xiàn)出上述規(guī)律。

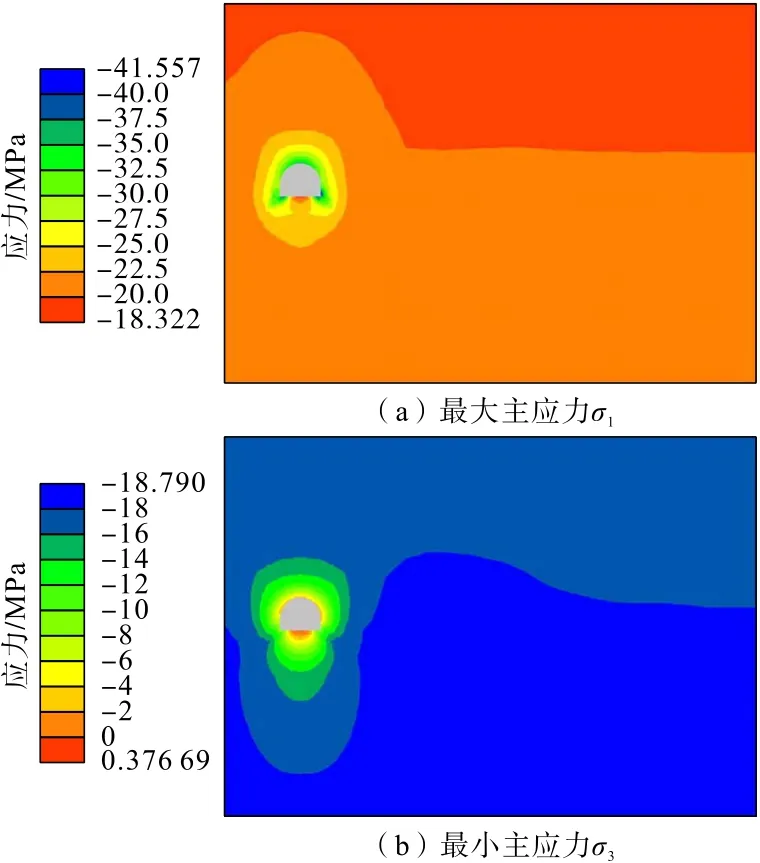
圖18 膠帶機巷開挖后應(yīng)力分布Fig.18 Stress distribution of belt conveyor roadway after excavation

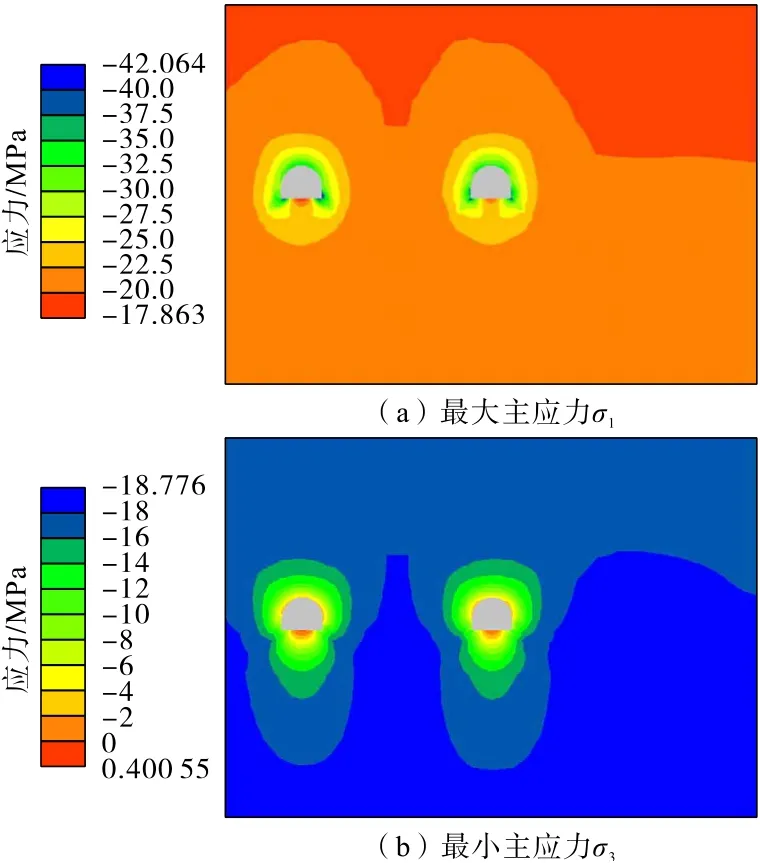
圖19 軌道巷開挖后應(yīng)力分布Fig.19 Stress distribution of track roadway after excavation

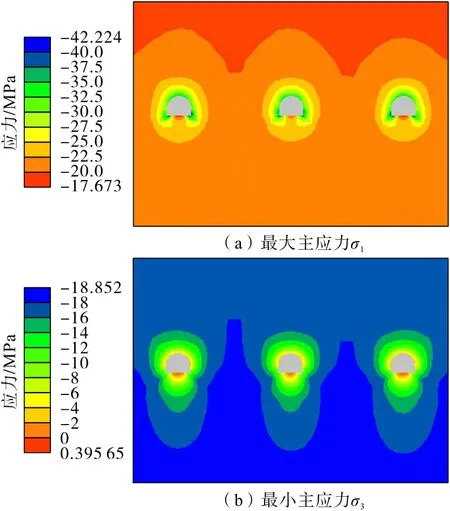
圖20 矸石膠帶機巷開挖后應(yīng)力分布Fig.20 Stress distribution of gangue belt conveyor roadway after excavation

3.3.2 位移分布

3 條巷道開挖后的位移分布如圖21所示。分析可知:膠帶機巷開挖后,巷道表面位移最大,其中拱頂下沉位移、兩幫收斂位移以及底鼓位移最為明顯,這與前述應(yīng)力分布規(guī)律分析結(jié)果相適應(yīng);鄰近軌道巷和矸石膠帶機巷開挖后也呈現(xiàn)出相同的變形規(guī)律,且相鄰巷道應(yīng)力疊加區(qū)域的位移分布發(fā)生變化。

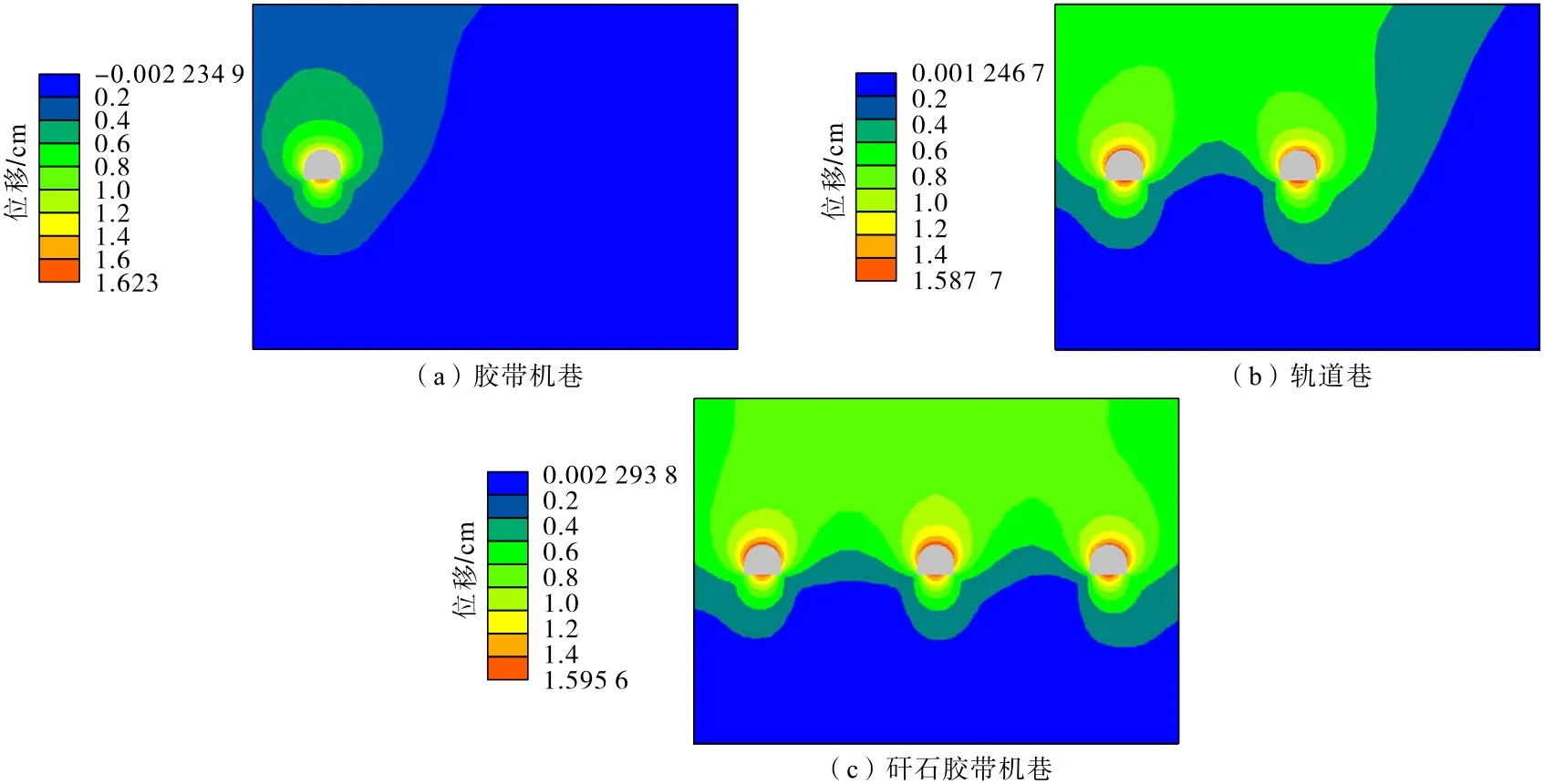
圖21 3 條巷道開挖后位移分布Fig.21 Displacement distribution the three roadways after excavation

3.4 注漿條件下巷道開挖計算分析

煤礦深部巷道開挖后圍巖發(fā)生變形,頂板下沉、兩幫收斂和底鼓是巷道變形最主要的表現(xiàn)形式,分步聯(lián)合支護方法和底板錨索治理是控制巷道變形的有效措施,然而這些方法和措施能夠有效發(fā)揮作用的關(guān)鍵在于注漿加固對圍巖的修復(fù)作用。為了研究注漿過程中巷道圍巖應(yīng)力及變形規(guī)律,在不施加其他支護措施情況下,本研究對單純注漿條件下的巷道圍巖應(yīng)力和位移進行計算分析。按照巷道施工工序,依次對膠帶機巷、軌道巷和矸石膠帶機巷開挖注漿后7、14、30 d 的巷道圍巖應(yīng)力和位移進行了計算,以注漿后7 d 和30 d 效果為例進行對比分析。

3.4.1 膠帶機巷注漿過程計算結(jié)果

膠帶機巷開挖注漿7 d 和30 d 后的應(yīng)力分布如圖22 和圖23所示。分析可知:膠帶機巷開挖注漿初期,最大主應(yīng)力在巷道外圍形成環(huán)形應(yīng)力集中,隨著注漿時間增加,最大主應(yīng)力逐漸向內(nèi)外兩側(cè)轉(zhuǎn)移,最終形成與未注漿條件下相似的應(yīng)力分布。巷道周圍最小主應(yīng)力范圍也隨著注漿時間增加而減小。應(yīng)力分布的這一變化過程較為真實地反映了圍巖隨時間的應(yīng)力轉(zhuǎn)移過程,開挖初期,巷道周圍巖體破碎,承載能力較低,其應(yīng)力通過圍巖變形來釋放,四周圍巖傳遞過來的應(yīng)力主要靠更深部的巖體承擔。隨著漿液固結(jié)時間增加,洞周圍巖體強度增加,抗變形能力也增大,能夠承受四周圍巖體傳遞過來的應(yīng)力,且變形也能夠得到有效控制。

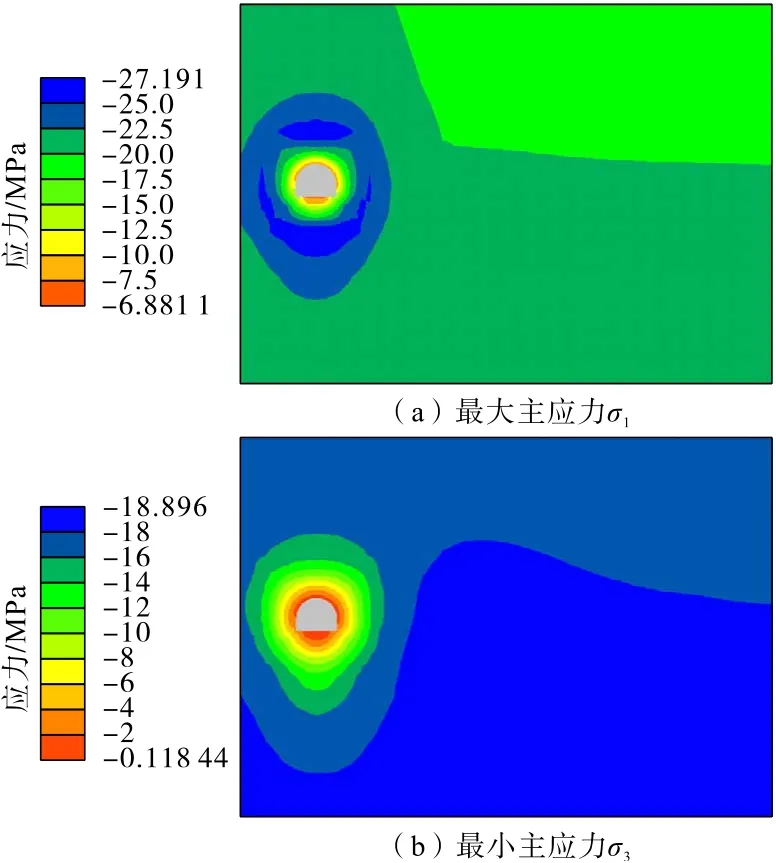
圖22 膠帶機巷開挖注漿(7 d)應(yīng)力分布Fig.22 Stress distribution of belt conveyor roadway after excavation grouting(7 days)

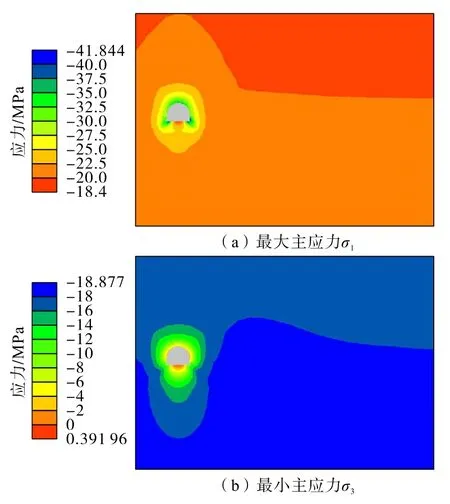
圖23 膠帶機巷開挖注漿(30d)應(yīng)力分布Fig.23 Stress distribution of belt conveyor roadway after excavation grouting(30 days)

膠帶機巷開挖注漿后的總位移分布如圖24所示。該圖顯示的位移分布與前述應(yīng)力分布相適應(yīng),膠帶機巷開挖注漿初期巷道圍巖最大變形主要在洞壁,主要為拱頂下沉、兩幫收斂和底鼓,隨著注漿固結(jié)時間增加,圍巖變形逐漸減小。

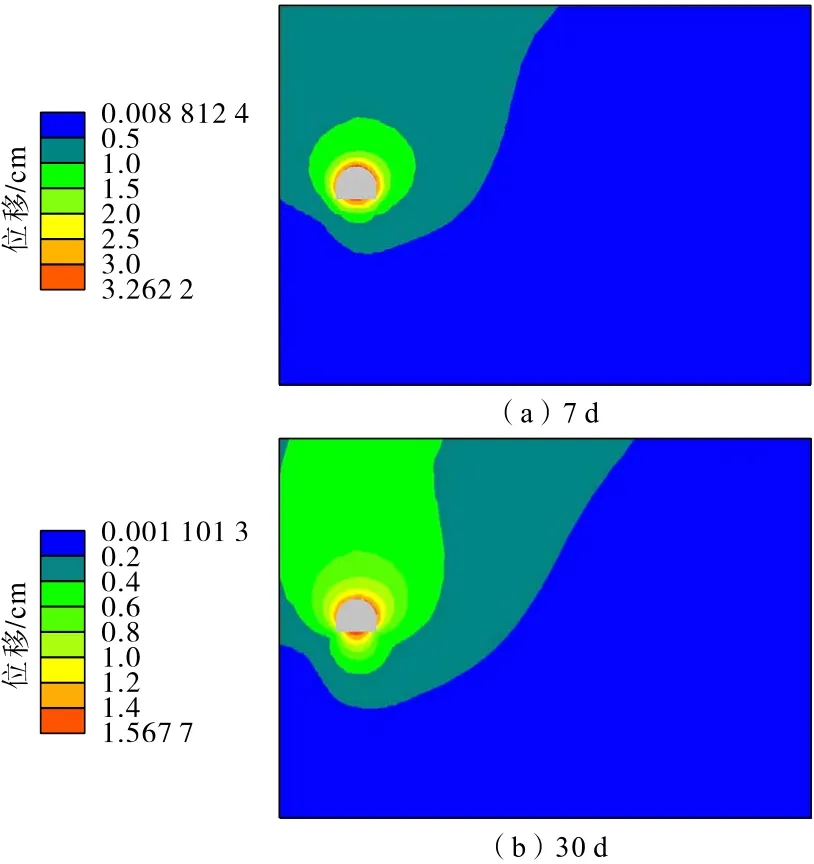
圖24 膠帶機巷開挖注漿后總位移分布Fig.24 Total displacement distribution of belt conveyor roadway after excavation and grouting

3.4.2 軌道巷注漿過程計算結(jié)果

軌道巷開挖注漿7 d 和30 d 后的應(yīng)力分布如圖25 和圖26所示。分析可知:軌道巷開挖注漿初期,巷道圍巖最大主應(yīng)力主要集中在左側(cè)已開挖注漿的膠帶機巷周圍,軌道巷周圍最大主應(yīng)力相對較小,隨著注漿時間增加,軌道巷周圍注漿固結(jié)體強度增大,所承擔的最大主應(yīng)力也逐漸增加,最終在兩條巷道周圍達到平衡。

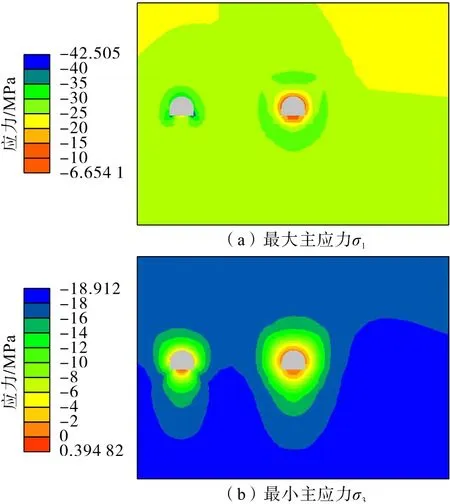
圖25 軌道巷開挖注漿(7 d)應(yīng)力分布Fig.25 Stress distribution of track roadway after excavation grouting(7 days)

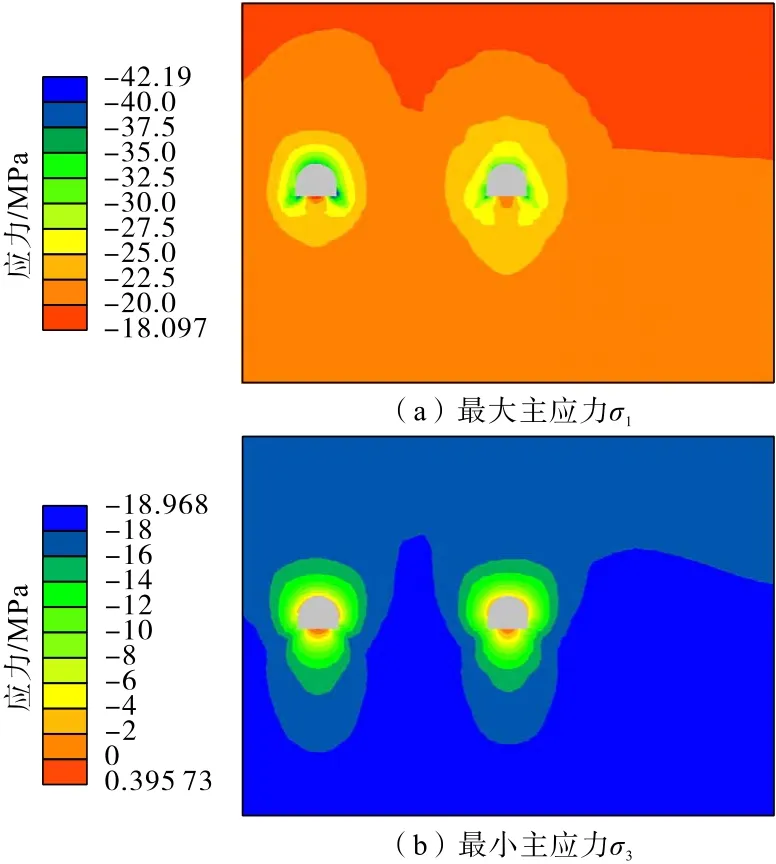
圖26 軌道巷開挖注漿(30 d)應(yīng)力分布Fig.26 Stress distribution of track roadway after excavation grouting(30 days)

軌道巷開挖注漿初期,巷道周邊巖體位移較大,隨著注漿固結(jié)時間增加,應(yīng)力在巷道之間調(diào)整,位移也逐漸向已經(jīng)注漿加固完成的膠帶機巷轉(zhuǎn)移,最后在膠帶機巷周圍巖體位移達到最大值,但位置總是比無注漿條件下巷道位移要小很多(圖27)。

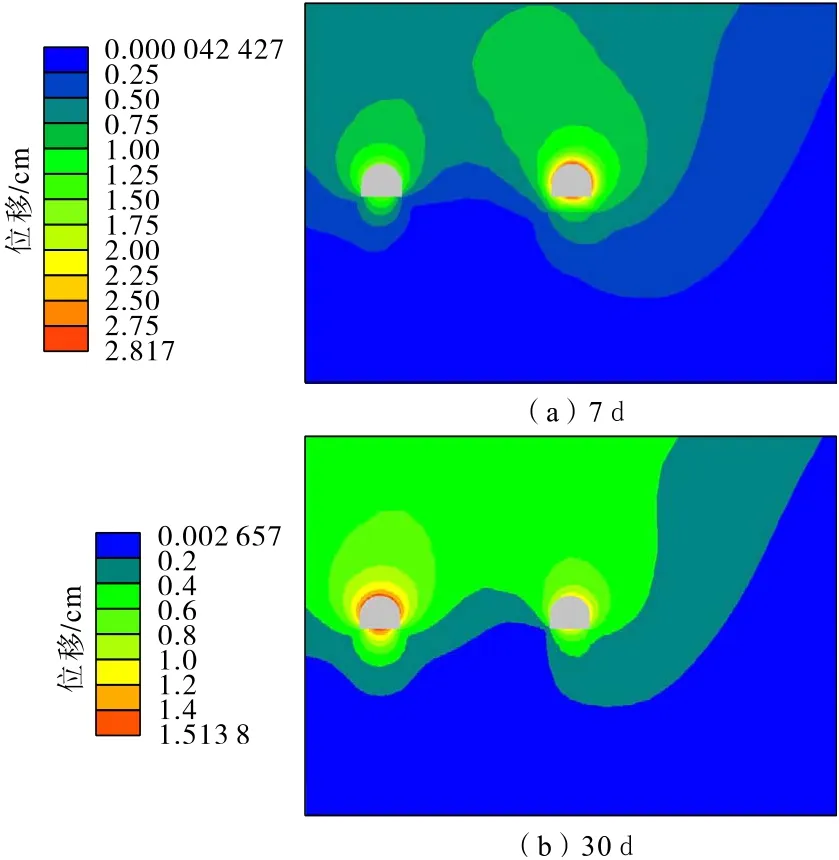
圖27 軌道巷開挖注漿后總位移分布Fig.27 Total displacement distribution of track roadway after excavation grouting

3.4.3 矸石膠帶機巷注漿過程計算結(jié)果

矸石膠帶機巷開挖注漿7 d 和30 d 后的應(yīng)力分布如圖28 和圖29所示。分析可知:矸石膠帶機巷開挖過程應(yīng)力分布規(guī)律與軌道巷相似,在開挖注漿初期,巷道圍巖最大主應(yīng)力主要集中在左側(cè)已開挖注漿的軌道巷和膠帶機巷周圍,矸石膠帶機巷周圍最大主應(yīng)力相對較小,隨著注漿時間增加,矸石膠帶機巷周圍注漿固結(jié)體強度增大,所承擔的最大主應(yīng)力也逐漸增加,最終3 條平行巷道周圍應(yīng)力達到動態(tài)平衡。

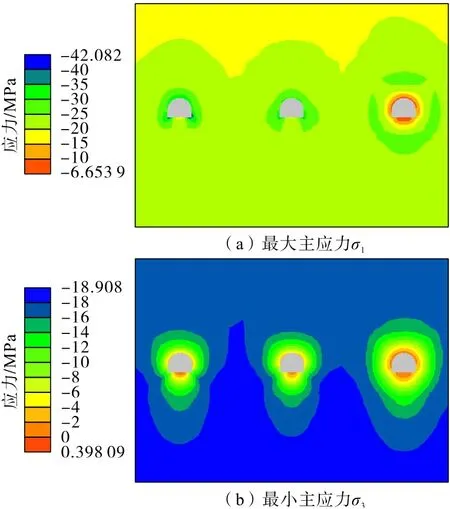
圖28 矸石膠帶機巷開挖注漿(7 d)應(yīng)力分布Fig.28 Stress distribution of gangue belt conveyor roadway after excavation grouting(7 days)

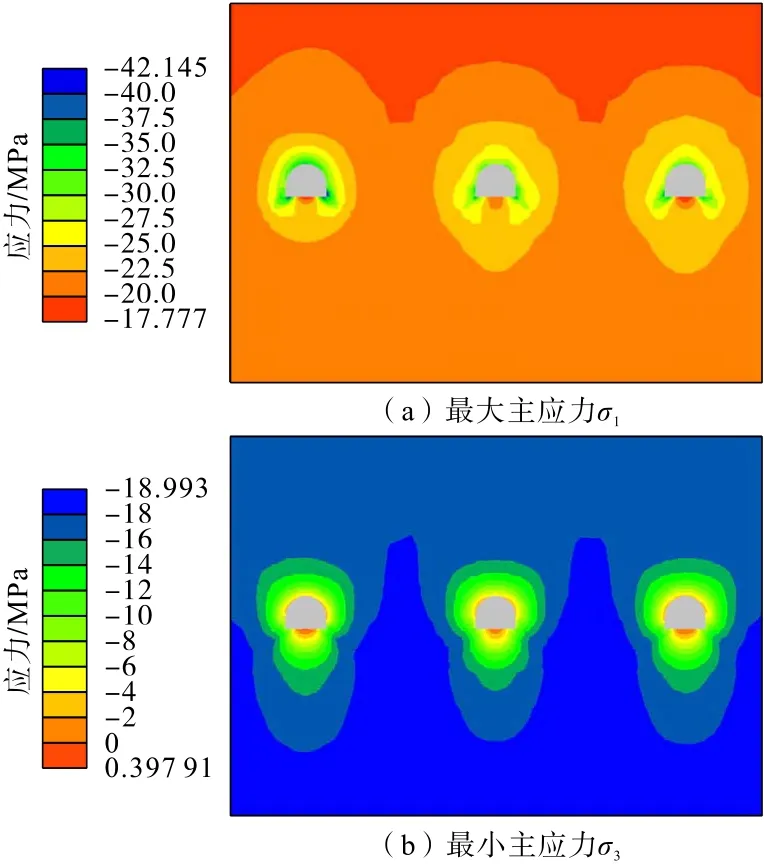
圖29 矸石膠帶機巷開挖注漿(30 d)應(yīng)力分布Fig.29 Stress distribution of gangue belt conveyor roadway after excavation grouting(30 days)

巷道開挖注漿初期,巷道周邊巖體位移較大,隨著注漿固結(jié)時間增加,應(yīng)力在巷道之間調(diào)整,位移也逐漸向已經(jīng)注漿加固完成的膠帶機巷和軌道巷轉(zhuǎn)移,最后在膠帶機巷周圍巖體位移達到最大值,軌道巷周邊位移次之,矸石膠帶機巷周邊位移最小(圖30)。與無注漿條件下巷道開挖后位移相比,3 條巷道位移值均大大減小,可見注漿加固對巷道圍巖變形控制起到了顯著作用。可見,本研究所提出的考慮圍巖孔隙特性的注漿加固評價的數(shù)值仿真分析方法能夠有效模擬巷道圍巖注漿加固效果。

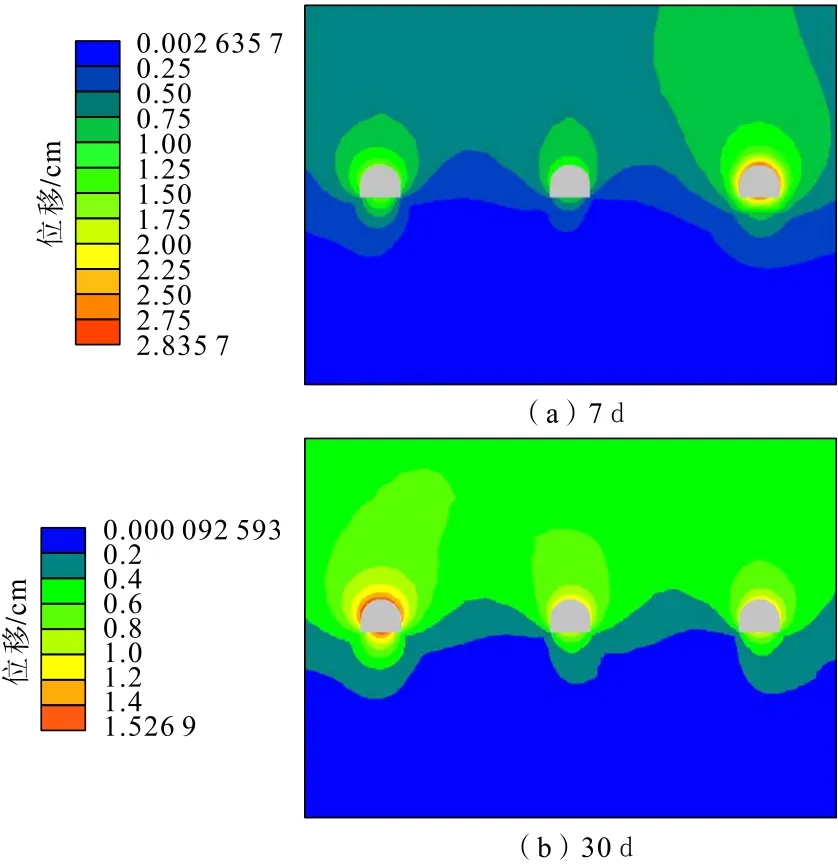
圖30 矸石膠帶機巷開挖注漿總位移分布Fig.30 Total displacement distribution of gangue belt conveyor roadway after excavation grouting

4 結(jié)論

以淮南礦區(qū)顧北煤礦深部巷道圍巖注漿加固工程為例,對煤礦深井巷道注漿固結(jié)體的力學(xué)特性進行了分析研究,在此基礎(chǔ)上對摩爾-庫倫本構(gòu)模型進行修正,開發(fā)了適合進行注漿加固評價的數(shù)值分析方法。所得到結(jié)論如下:

(1)孔隙率對注漿固結(jié)體的強度和變形特性影響較大。隨著孔隙率增加,注漿固結(jié)體的彈性模量逐漸增大,單軸抗壓強度也呈增大趨勢;相同圍壓下,隨著孔隙率增加,注漿固結(jié)體峰值應(yīng)力逐漸增加;隨著圍壓增加,注漿固結(jié)體的殘余強度逐漸增加,且破壞模式逐漸向延性破壞轉(zhuǎn)變。注漿固結(jié)體的黏聚力隨著孔隙率的增大呈增長趨勢,符合對數(shù)函數(shù)關(guān)系;而內(nèi)摩擦角隨孔隙率增大而減小。

(2)注漿固結(jié)體主要包括包裹和搭接兩種膠結(jié)模式。注漿固結(jié)體的力學(xué)特性與其膠結(jié)模式之間存在密切聯(lián)系。

(3)以摩爾-庫倫模型為基礎(chǔ),通過模量修正和強度修正,建立了適合注漿固結(jié)體的修正的摩爾-庫倫本構(gòu)模型,并通過FLAC3D軟件自定義本構(gòu)模型功能,建立了煤礦深部巷道注漿加固數(shù)值分析方法。該方法能有效反映煤礦深部巷道注漿加固過程中的應(yīng)力和位移變化特征,可為煤礦深部巷道注漿加固設(shè)計和施工提供分析評價方法。