基于三角函數(shù)擬合的改進型S 型加減速算法設計
孟寶星,王成勤
(徐州工業(yè)職業(yè)技術學院,江蘇 徐州 221140)
0 引言
步進電機的轉動是通過電機驅動器產(chǎn)生控制脈沖信號實現(xiàn)的。電機驅動器會產(chǎn)生不同頻率和數(shù)量的脈沖來控制步進電機的速度和位移[1]。目前國內外常用的電機控制器的加減速曲線有:梯形加減速曲線、分段線性加速曲線、指數(shù)加減速曲線以及S 型加減速曲線,其中梯形加減速曲線原理簡單,速度為時間的一階導數(shù),實現(xiàn)容易,能滿足絕大應用場景,具有較高的性價比,應用廣泛。但是由于梯形加減速的加速度為常量,即加加速度為沖擊函數(shù),會對電機造成不必要的柔性沖擊,影響電機的使用壽命。一些高性能的電機控制器會采用S 型加減速來解決梯形加減速存在的問題。S 型加減速模式雖然優(yōu)于梯形加減速模式,但其仍然存在加加速度突變,會對系統(tǒng)造成一定程度的振動,更重要的是S 型加減速模式在求解過程中存在多階函數(shù),其運算量較高且復雜,而傳統(tǒng)的步進電機控制需要高達上千赫茲的脈沖發(fā)生速度,這會消耗較大的運算資源,這使得采用S 型加減速的驅動器成本相對偏高[2]。
蔡娜等[3]設計了一種新的可實時實現(xiàn)的拋物線型速度給定算法。這種算法響應速度更快,控制精度更高,減少了失步、過沖現(xiàn)象的發(fā)生率,避免了機械柔性沖擊,但對系統(tǒng)要求仍然較高。周黎等[4]提出了一種“正矢型”加減速曲線,實現(xiàn)了對步進電機的精準控制,減少了失步過沖現(xiàn)象的發(fā)生率,但動態(tài)響應速度較慢。
1 步進電機控制系統(tǒng)概述
步進電機常用于各種運動控制系統(tǒng)當中,是一種常用的控制執(zhí)行部件,主要有反應式、永磁式和混合式三種類型。從繞組數(shù)目分類來看主要有兩相、三相和五相步進電機。目前市面上最常見的步進電機為兩相混合式步進電機,大約占有97%以上的市場份額。主要針對兩相混合式步進電機系統(tǒng)進行討論。
步進電機驅動器,是一種將電脈沖信號轉換為電機角位移的驅動執(zhí)行器。如圖1 所示。由于步進電機本身是運動部件,在運動過程中會產(chǎn)生慣性。在步進電機控制的過程中,速度不能發(fā)生突變,否則會對其機械結構產(chǎn)生較大的沖擊,一般稱其為剛性沖擊。如果加加速度產(chǎn)生突變,也會造成電機磨損。最理想的情況是:電機運動的速度、加速度及加加速度皆連續(xù)且可導,可以最大程度的避免電機運行過程中造成電機的磨損。這也是在步進電機驅動過程中需要引入電機加減速的原因。
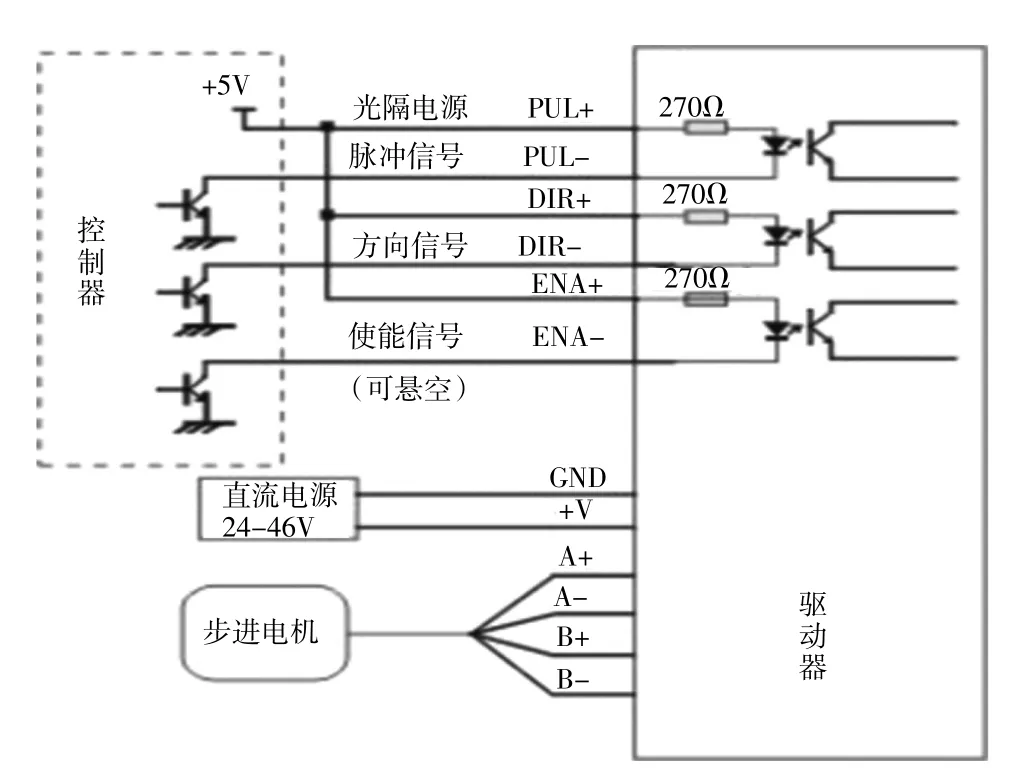
圖1 步進電機驅動器結構框圖
分析了傳統(tǒng)S 型加減速的基本原理,并分析了它存在的局限性。為了解決上述問題,引入了改進型的S 型加減速算法,利用三角函數(shù)擬合S 型加減速的變加速階段,將三角函數(shù)的導數(shù)轉換為移位運算,從而顯著降低算法的計算量,具有較高的適用性。
2 傳統(tǒng)S 型加減速算法解析
S 型加減速曲線名稱是由系統(tǒng)在加減速階段的速度曲線形狀呈S 形而得來的,采用降速與升速對稱的曲線來實現(xiàn)升降速控制。正常情況下的S 曲線運行過程可分為加加速段、勻加速段、減加速段、勻速段、加減速段、勻減速段和減減速段7 段。在變加減速區(qū),加速度的導數(shù)為恒值;恒加減速區(qū),加速度為恒值;勻速段的速度為恒值,加速度為零。S 形加減速在任何一點的加速度都是連續(xù)變化的,從而避免了柔性沖擊,速度的平滑性很好,運動精度高[2]。
根據(jù)加減速階段的7 段模型,設S為行駛位移,J為加加速度,A為加速時加速度,DA為減速時加速度,Vmax為電機的最大速度,Vs為電機的起始速度,Ve為電機的終止速度,fa為加速度函數(shù),fj為加加速度,fv為速度函數(shù),fs為位移函數(shù)。在S 型加減速模型中A不是固定值,所以可以設置Amax為加速時最大加速度,Dmax為減速時最大加速度,同樣在設定Amax=Dmax,Vs=Ve的情況下進行討論,其他方向上同理。
標準的S 型加減速是以加加速度為恒定值來進行建模,所以fj的函數(shù)表示如下:
由此可以得到fa的函數(shù)表達為:
定義一組數(shù)值代入公式可以得到相應的函數(shù)曲線,假設J= 200,Amax= 100,Vmax= 200,Vs= 30,S=0,便可以畫出fj和fa,以及fv和fs的函數(shù)圖形,如圖2、3 所示。
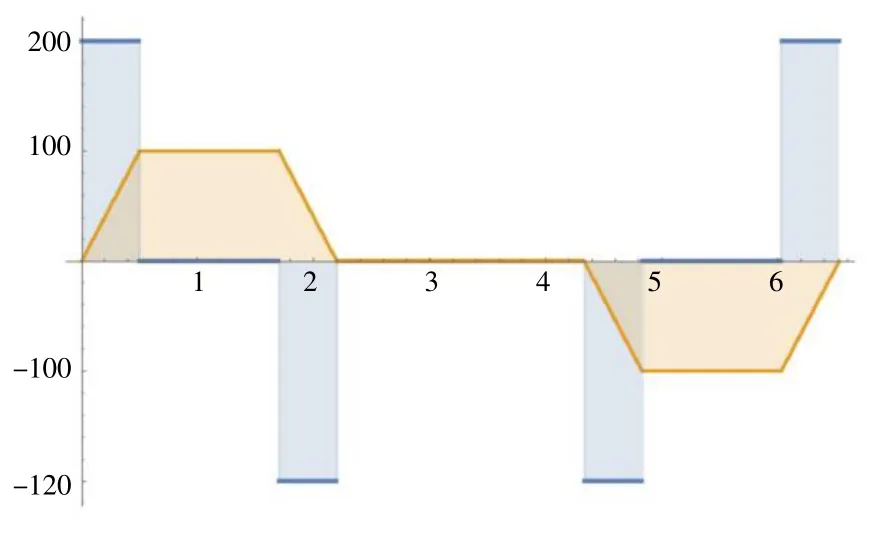
圖2 S 型加減速fj 和fa 函數(shù)圖形
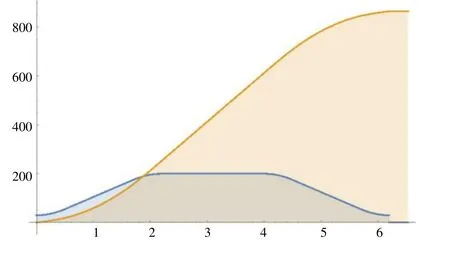
圖3 S 型加減速fv 和fs 函數(shù)圖形
通過仿真得到了S 加減速的模型,但是同時也發(fā)現(xiàn)在計算fv的公式中出現(xiàn)了大量的4 次方的運算,在執(zhí)行S 型加減速的計算過程中需要頻繁的進行開四次根的計算,由于在實際應用過程中電機控制的脈沖頻率一般可以達到200 K 左右,這需要強大的算力保障,且S 型加減速依然存在加加速度的突變,在一定程度上也會造成設備的振動。故此一般傳統(tǒng)的低端步進電機控制產(chǎn)品普遍采用梯形加減速算法,而沒有采用S 型加減速算法,這樣的確降低了控制器成本和研發(fā)難度,但是也導致了電機的性能和壽命的降低,穩(wěn)定性也受到了不小的影響[5]。
3 改進型S 形加減速算法設計與實現(xiàn)
通過上文的分析,可以看到S 型加減速的基本原理及其存在局限性,S 型加減速的局限性主要在于其加加速度依然存在突變,這樣依然會在一定程度上導致設備的振動和磨損,且S 型加減速算法的運算過程中存在4 階函數(shù),其在工程應用中對控制器的性能提出了較高的要求,這樣大大提高系統(tǒng)的復雜度和成本。
S 型加減速存在的問題主要存在于7 段控制模型中的加加速模式和減加速模式,在S 型加減速算法中,引入了加加速度J的概念,且在加加速和減加速狀態(tài)下J為常量。如果把J從常量狀態(tài)定制為多階可導的三角函數(shù)模型,便從數(shù)學建模的角度解決了加加速度突變的問題。
所以在改進型的算法中,引入Jmax為最大加加速度,并在加加速度階段設定加加速度的曲線定義為:
其中定義:
上文中t3時間段為電機在保持Vmax勻速運動的階段,所以可以通過積分計算出加速和減速時間段的位移,假設加速階段的位移為Sa,減速階段的位移為Sd,則可以得到:
通過上述算式可以發(fā)現(xiàn),當t = t1時,J= 0。這樣便確保了加加速度的連續(xù)性,依次代入t=t1+ t2,t= 2t1+ t2,t=t1+ t2,t= 2t1+ t2+ t3,t=3t1+ t2+ t3,t= 3t1+2t2+ t3幾個時間點,均可以得到J= 0。這樣確保了加加速度的連續(xù)性,根據(jù)fj的函數(shù)表達,可以得出fa的函數(shù)表達為:
代入t在各個時刻的值,可以發(fā)現(xiàn)加速度A依然連續(xù)且可導,然后根據(jù)加速度函數(shù)便可以得到速度的函數(shù)表示如下:
得到速度函數(shù)帶入求速度對時間的積分,得到位移。
定義一組數(shù)據(jù)Jmax= 200,Amax= 100,Vmax= 200,Vs=Ve= 30,S= 800,便可以畫出fj和fa,以及fv和fs的函數(shù)圖形,如圖4、5 所示。

圖5 改進型S 型加減速fv 和fs 函數(shù)圖形
在實際的求解過程中可以發(fā)現(xiàn)整個函數(shù)本身還是遵循梯形加減速的加速、勻速及減速三個階段,S型加減速是指把加速階段又分為加加速階段,勻加速階段和減加速階段,減速階段為加速階段相反。且在三角函數(shù)擬合的S 型加減速中,是根據(jù)加速階段和減速階段的位移,得到勻速階段的位移情況,最終計算出勻速階段的時間。所以在求解的時,可以把加速階段,勻速階段和減速階段分別求解。舉例說明如下:
例如在2t1+t2+t3開始的減速階段,定義其實時間為2t1+t2+t3,定義該時間變量為tt,便可以得到:
該函數(shù)與加速階段的函數(shù)基本一致,支持改為負值。這樣便可以把整個三角函數(shù)分為3 段進行分析的話,可以大大減小運算量,如果在硬件計算中引入并行計算,便可以大大提升系統(tǒng)的運行效率,滿足實時性、精度和資源占用等方面的要求[6]。
4 改進型S 形加減速中的三角函數(shù)求解問題
改進型S 型加減速算法,其需要的計算均為三角函數(shù)計算,可以通過查表法將三角函數(shù)求導轉換為移位運算。其思路如下:要計算一個角度θ的三角函數(shù)值。首先,選擇一個初始的量(x0,y0),通常設為(x0,0),表示初始角度為0 的向量,x0的值一般根據(jù)經(jīng)驗選擇,特定的值可以在保證一定精度的前提下減少迭代的次數(shù);然后,將目標角度θ分解成一系列旋轉操作,每次旋轉一個小的角度。在每次旋轉之后,通過縮放操作來逼近目標角度的三角函數(shù)值。
因為數(shù)據(jù)的右移n位相當于乘以2(-n),于是可以將初始縮放因子設置為1,0,每次迭代減半,假設縮放因子為gain,便可以得到
其中,d表示旋轉方向(或者),矢量(x0,y0)逆時針旋轉角度得到的值的表達式為:
因把cosθ去掉不影響求值的結果,得到:
以tanθ作為縮放因子,建立一個縮放因子表格,建立從2(0),2(-1),2(-1)的表格,然后通過迭代查表,便可以計算出θ的角度值。
表1 為設置最高17 次迭代的縮放因子表格。
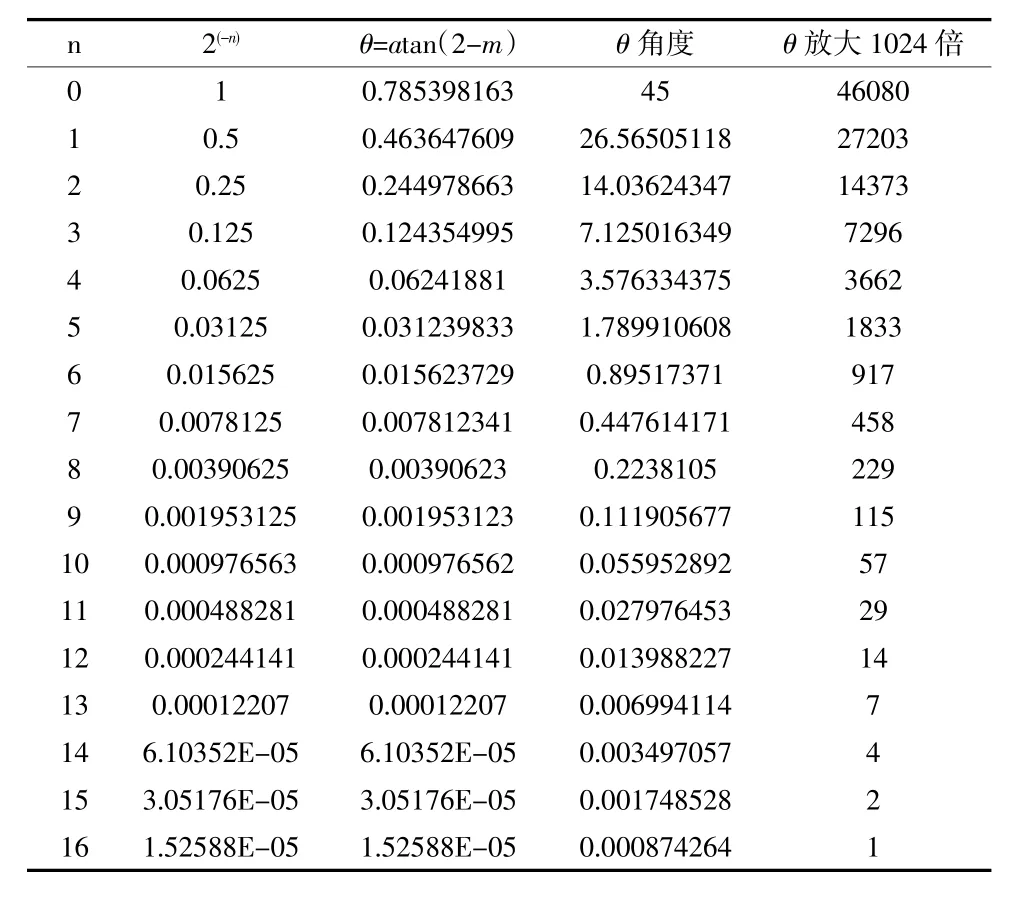
表1 縮放因子表格
表1 除了計算縮放因子對應的值,還把求取角度之后放大1024 倍的取整值也給出,目的是考慮到在嵌入式環(huán)境中,對浮點數(shù)的運算比較耗費時間,且1024 也剛好是數(shù)據(jù)左移10 位的值。如便可以簡單實現(xiàn)三角函數(shù)的快速實現(xiàn),
下面是該算法的核心部分C 語言代碼:
include #include #define M_PI 3.14159265358979f #define TABLE_SIZE 17 // 迭代次數(shù) //按照角度擴大1024 倍運算 static const int atanTable [TABLE_SIZE] = {46080,27203, 14373,7296,//83662,1833,917,458,//128229,115,57,29,//204814,7,4,2,//327681 }; // Cordic 算法計算正弦和余弦 //最小值:0.001,小于這個值為0 度,不需要判斷 void cordic(double angle,double*sinVal,double*cosVal) { int x = 35628; int y = 0; int z = 0; int nextX,nextY,nextZ; angle = angle*180 / M_PI; int unit =((int)angle))/ 90; angle =((int)angle))% 90; z =(int)round(angle*1024); for(int i = 0; i < TABLE_SIZE; i++) { if((abs(z)<= 1) { break; } else if(z >0) { nextX = x -(y >>i); nextY = y +(x >>i); nextZ = z - atanTable[i]; } else { nextX = x +(y >>i); nextY = y -(x >>i); nextZ = z + atanTable[i]; } x = nextX; y = nextY; z = nextZ; } double val = sqrt((double)x*x +(double)y*y); switch(unit) { case 0: *sinVal =((double)y)/ val; *cosVal =((double)x)/ val; break; case 1: *sinVal =((double)x)/ val; *cosVal = -((double)y)/ val; break; case 2: *sinVal = -((double)y)/ val; *cosVal = -((double)x)/ val; break; case 3: *sinVal = -((double)x)/ val; *cosVal =((double)y)/ val; break; } } int main(){ double angle = -20.0*M_PI/180; // 待計算的角度,以弧度為單位 double sinValue,cosValue; cordic(angle,&sinValue,&cosValue); // 使用Cordic 算法計算正弦和余弦 printf("Angle:%.2f
",angle); printf("Sin:%.4f
",sinValue); printf("Cos:%.4f
",cosValue); return 0; } 以下是一段基于cortex-M3 內核的控制器執(zhí)行效率對比代碼,以0.01 弧度作為單位,對0-6.28 進行正弦和余弦計算,如下: angle = 0; runtime_start(); for(i = 0; i < 628; i++) { angle += 0.01; cordic(angle,&sinValue,&cosValue); } runtime_stop(); printf("cordic time:%d.
",(time_cnt<<16)|runtime); angle = 0; runtime_start(); for(i = 0; i < 628; i++) { angle += 0.01; sinValue = sin(angle); cosValue = cos(angle); } runtime_stop(); printf("math time:%d.
",(time_cnt<<16)|runtime); 測試的結果如下: 三角函數(shù)轉化位移時間為:11971 個機器時間周期; 普通三角函數(shù)運算時間為:58413 個機器時間周期。 可見在傳統(tǒng)的嵌入式系統(tǒng)當中,采用三角函數(shù)轉換為移位運算的執(zhí)行效率,為普通三角函數(shù)運算性能的4.8 倍。 在步進電機控制系統(tǒng)中為了解決電機在運行過程中會產(chǎn)生剛性沖擊、柔性沖擊以及加加速度突變產(chǎn)生的設備振動問題,對傳統(tǒng)的加減速模型進行改進,根據(jù)三角函數(shù)多階連續(xù)可導的性質,引入三角函數(shù)曲線擬合,提高系統(tǒng)的穩(wěn)定型,且在運算性能有限的場景中,也可以快速的利用查表法進行三角函數(shù)的求解,把三角函數(shù)運算轉化加減和移位運算。避免了不必要的快速浮點和求階運算,大大提升了系統(tǒng)的運行效率,降低系統(tǒng)的成本。5 結語

