基于譜圖小波閾值的機床主軸振動數(shù)字信號降噪研究＊

張新文 周苗苗 李金輝

（①河南交通職業(yè)技術學院汽車學院，河南 鄭州 450005；②鄭州旅游職業(yè)學院機電工程學院，河南 鄭州451464；③河南科技大學車輛與交通學院，河南 洛陽 471003）

數(shù)字信號已經(jīng)成為工業(yè)領域智能化應用的關鍵因素之一，可以通過數(shù)控機床運行過程中數(shù)據(jù)特征采集來監(jiān)測其加工控制性能、部件磨損程度、故障特征分析和誤差測定等指標[1-3]。但在采集與傳輸數(shù)字信號期間，實際測試數(shù)據(jù)會受到儀器、環(huán)境條件與人為操作的綜合作用，導致采集獲得的實際信號存在噪聲成分，無法根據(jù)信號特征判斷機床實際運行狀況[4-5]。這就要求進行特征參數(shù)提取并對信號實施降噪分析。

進行數(shù)字信號處理時，需要將數(shù)據(jù)由初始域映射至其余域，目前已經(jīng)形成了離散傅里葉轉換（DFT）、變分模態(tài)分解（VMD）、希爾伯特轉換（HT）、小波轉換（WT）等多種方法[6-8]。隨著研究的深入，還有學者對譜圖小波轉換（SGWT）開展了深入探討，與加權圖信號傅里葉轉換過程相近，利用譜圖理論以及經(jīng)典小波轉換的方法，再結合頻譜特征進行分解得到特定頻率范圍子帶，從而保證在譜圖域內(nèi)完成圖信號分析的功能[9-12]。Deutsch S等[13]在譜圖小波轉換基礎上設計了一種光滑流形降噪技術，可以保留總積累能量比閾值更高的低頻尺度與譜圖小波系數(shù)，再將剩余高頻譜圖小波系數(shù)去除后，達到二維圖像降噪效果。王林等[14]開發(fā)了一種通過譜圖小波轉換方法實現(xiàn)的圖像壓縮編碼算法，能夠在高壓縮比條件下形成精細重構圖像。進行三維實體應用時，Masoumi M 等[15]以譜圖小波轉換方法構建得到評價三維模型特征的框架，可以分別完成三維模型局部與全局特征的捕捉控制，由此完成三維實體外形的準確檢索。胡玲等[16]在構建模型過程中加入譜圖小波轉換方法，建立了模型分辨系統(tǒng)，完成多種外形的精確分辨并獲得優(yōu)異魯棒性。

根據(jù)以上分析可知，譜圖小波轉換對于平面圖像數(shù)據(jù)處理領域都發(fā)揮了重要作用。本文根據(jù)譜圖小波轉換理論與實際應用過程，構建了一種可以對一維數(shù)字信號進行分析的譜圖小波閾值降噪（SWTD）算法，再通過仿真信號與機床主軸振動信號降噪的方式驗證了譜圖小波閾值降噪可靠性。

1 譜圖小波閾值降噪方法

1.1 基于譜圖理論

完成一維數(shù)字信號的定義后得到路圖信號，將一維數(shù)字信號時序性與路圖序列進行匹配后，確保信號時間序列與路圖節(jié)點相匹配。

采用Gauss 權值函數(shù)確定路圖信號節(jié)點權值，再利用譜圖理論建立對角矩陣D、鄰接矩陣W、拉普拉斯矩陣L，使一維數(shù)字信號信息存儲至路圖信號矩陣內(nèi)。路圖信號具備簡單結構，鄰接矩陣W與拉普拉斯矩陣L屬于一種簡單形式，在鄰接矩陣W中數(shù)值只存在于次對角部位，其余元素取值都是0；拉普拉斯矩陣L只有主對角與次對角元素有值，剩余各元素都是0。

小波核g屬于接近原點區(qū)域的一元冪，當x增大后會引起冪律減小的結果，存在g(0) = 0。本次采用三次樣條譜圖小波核進行譜圖小波轉換，建立下述表達式：

式中：尺度t取決于拉普拉斯特征值上限、譜圖小波轉換參數(shù)K與分解層數(shù)J。設定拉普拉斯特征下限λmin=λmax/K，可以確定最大尺度t1= 2/λmin，最小尺度tm=1/λmax，符合對數(shù)等差分布規(guī)律。

1.2 閾值及閾值函數(shù)選取

選擇合理閾值可以實現(xiàn)有效降噪，但有用信號也會被判斷成噪聲而去除；對含有較少高頻信息的信號實現(xiàn)良好降噪性能，能夠提取微弱信號。在分析特定信號的過程中應先對信號分布頻率進行理論分析，由此確定合適閾值。本研究中機床主軸振動信號基本都屬于低頻段，閾值κ計算以下表達式：

式中：N代表尺度tj子帶譜圖小波系數(shù)的數(shù)量；σj代表第j子帶中的噪聲標準差，根據(jù)式（4）進行估計。

式中：dj(k)代表第j子帶第k個譜圖小波系數(shù)；0.65 代表數(shù)據(jù)分布參數(shù)。

利用特定閾值函數(shù)來實現(xiàn)譜圖小波系數(shù)處理的功能，包含硬閾值與軟閾值兩種函數(shù)表達式，建立式（5）和式（6）。

式（5）和式（6）中，wjk表示最初確定的譜圖小波系數(shù)，wˉjk表示采用閾值函數(shù)進行處理得到的譜圖小波系數(shù)。

軟閾值函數(shù)屬于一種連續(xù)函數(shù)，未出現(xiàn)跳躍點，處理得到了更加連續(xù)的譜圖小波系數(shù)，重構信號也沒有出現(xiàn)附加振蕩，可以實現(xiàn)良好平滑性。本研究以軟閾值函數(shù)進行處理。

1.3 譜圖小波閾值降噪流程

圖1 所示為譜圖小波閾值降噪流程[10]。

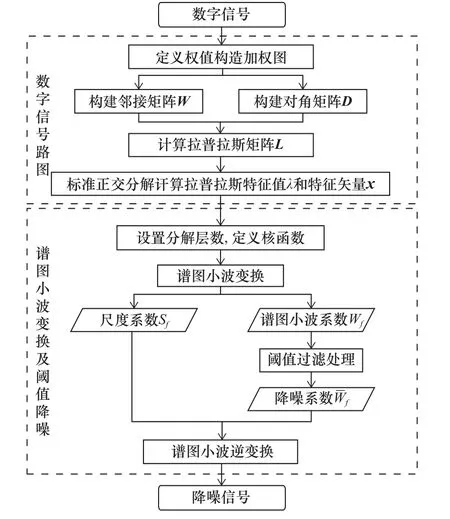
圖1 譜圖小波閾值降噪算法流程圖

（1）在路圖上定義一維數(shù)字信號，之后建立加權圖G，再以權值函數(shù)構建鄰接矩陣W與對角矩陣D，設置拉普拉斯矩陣L=D-W，之后計算其特征值λ與特征矢量x。

（2）確定分解層數(shù)后，綜合運用譜圖小波核與尺度函數(shù)核，并通過SGWT 完成譜圖信號的小波轉換，從而計算出尺度系數(shù)Sf與譜圖小波系數(shù)Wf。

（3）獲得低通頻率尺度系數(shù)后，再對譜圖小波系數(shù)子帶閾值σj進行計算，之后通過閾值函數(shù)實現(xiàn)譜圖小波系數(shù)的過濾。||wjk≥σj情況下，則通過閾值函數(shù)實施處理；反之將其取值設定為0。

（4）對步驟（3）確定的尺度系數(shù)與譜圖小波系數(shù)開展譜圖小波逆轉換獲得降噪信號。

綜合考慮可以發(fā)現(xiàn)，本文先通過尺度函數(shù)獲取低頻信息再將其保存至尺度參數(shù)中，接著以閾值對存在少量低頻信息與大量高頻數(shù)據(jù)的譜圖小波系數(shù)實施過濾。譜圖小波系數(shù)中只存在較低比例的低頻參數(shù)，大部分都是由噪聲構成，進行估計可以獲得很高的噪聲標準差準確率，確保得到精確閾值計算結果，達到充分去除噪聲的效果。但在經(jīng)典小波轉換過程中，有用信息與噪聲在小波系數(shù)中呈現(xiàn)混合狀態(tài)，對閾值過濾的標準差估計值產(chǎn)生共同作用。在高頻小波系數(shù)子帶中，噪聲處于主導地位，可以完成噪聲標準差的精確估計；而在低頻小波系數(shù)子帶中，有用信息占據(jù)主導地位，不能對噪聲標準差進行準確估計。如果噪聲標準差過大，則會導致其中有用信息也被大量去除；否則，會造成降噪程度偏低的情況。與常規(guī)小波閾值降噪方法相比，采用本文方法在理論層面具備更大優(yōu)勢。而且還可以發(fā)現(xiàn)，采用本文方法可見處理時是針對譜圖域中譜圖小波系數(shù)直接完成一次性數(shù)據(jù)過濾，不用進行迭代計算，可以實現(xiàn)更高的處理效率。

2 工程應用

2.1 機床主軸振動信號采集

為驗證采用本文方法可以滿足有效降噪的目標，選擇某Y38A 型汽車傳動件用滾齒機加工機床主軸振動信號進行測試。得到表1 與表2 的滾齒機加工信息，圖2 所示為振動信號采集系統(tǒng)的儀器分布情況。將PCB 加速度測試儀安裝于機床主軸支座處，以10 000 Hz 的頻率采集獲得z向振動頻率。振動信號通過加速度傳感器與信號調(diào)節(jié)儀傳輸?shù)接涗泝x內(nèi)，由此確定振動信號的時域波形。滾齒加工屬于一種斷續(xù)切削的狀態(tài)，由此得到具有周期性特征的非線性機床主軸振動信號，具體如圖3 所示。

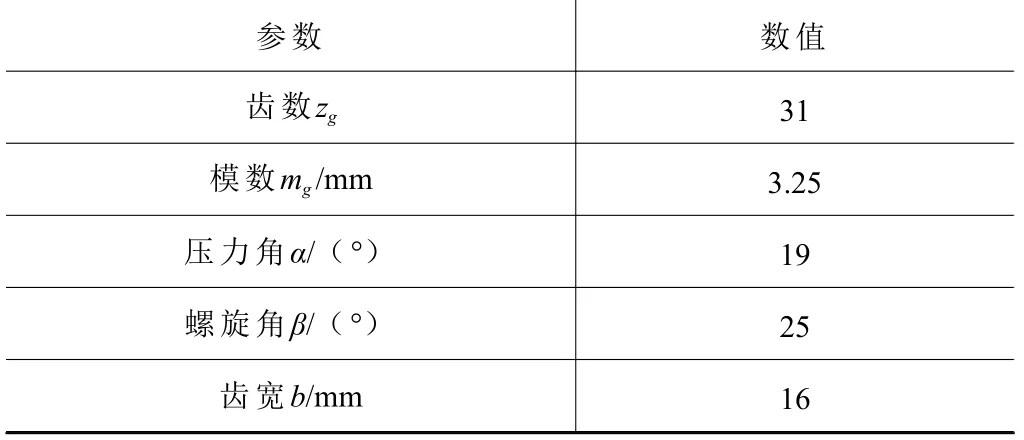
表1 工件基本參數(shù)

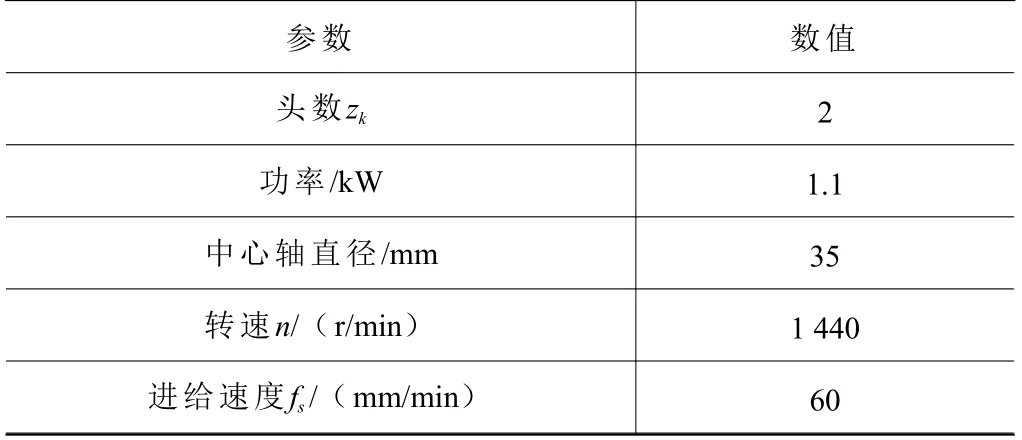
表2 機床基本參數(shù)

圖2 振動信號采集系統(tǒng)儀器布置

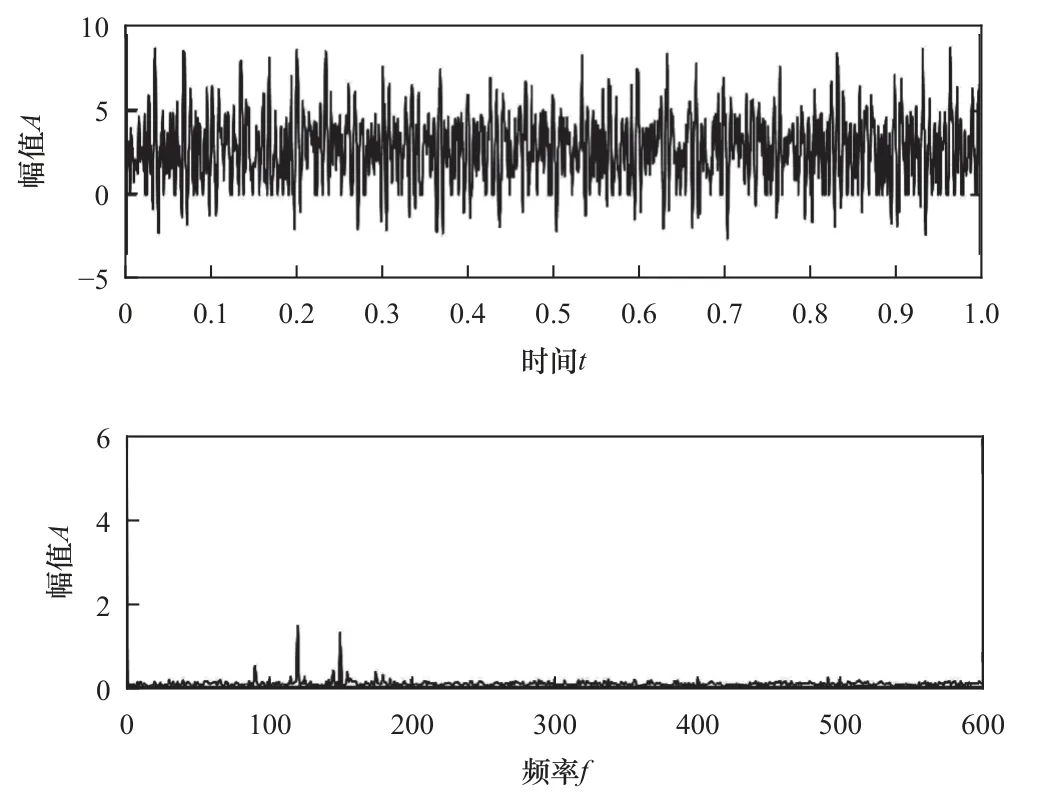
圖3 機床主軸振動信號

2.2 信號包絡譜分析

包絡譜算法是先完成信號的Hilbert 轉換處理再對其實施FFT 轉換，由此確定包絡譜，可以非常高效將復雜信號內(nèi)獲取有用數(shù)據(jù)。主軸包絡譜內(nèi)包含的主要有用頻率為自轉頻率與滾切頻率。表3 給出了主軸的自轉頻率與倍頻數(shù)據(jù)。表4 為滾切頻率與倍頻參數(shù)。

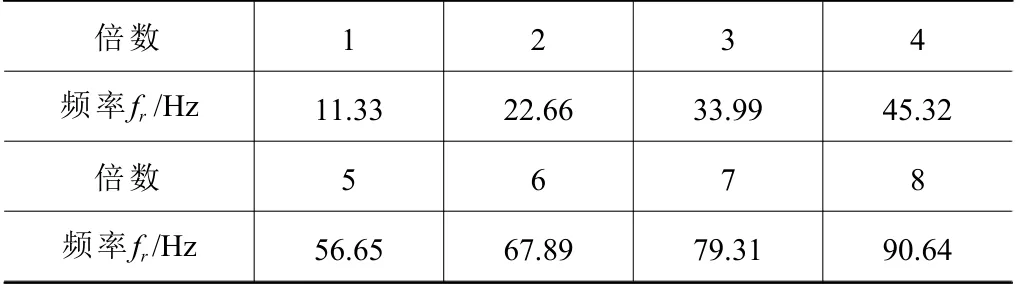
表3 主軸自轉頻率及其倍頻

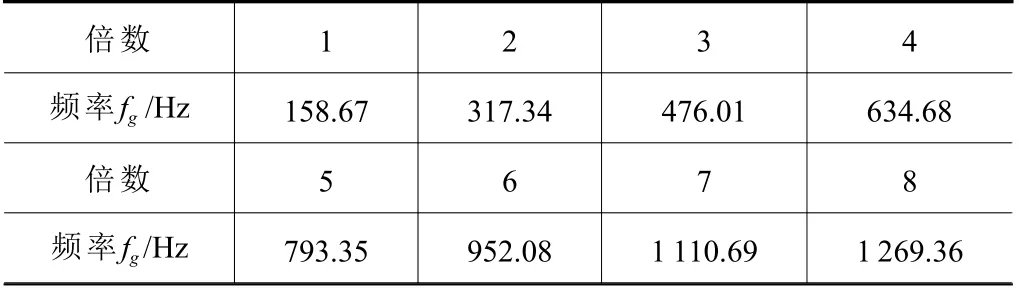
表4 滾切頻率及其倍頻

根據(jù)表3 與表4 的理論分析可知，機床主軸振動信號包含的有用頻率基本都處于400 Hz 范圍內(nèi)的低頻區(qū)。接著對實測機床主軸振動信號開展包絡譜處理，得到圖4 中的包絡譜信息以及圖5 中的分解圖。綜合分析圖4 和圖5 可以發(fā)現(xiàn)，實際測定的機床主軸振動信號頻率和理論計算結果相符，可以推斷超過400 Hz 的高頻段信號以噪聲為主，基本都是分布于400～1 000 Hz 頻率區(qū)內(nèi)。可以將降噪過程理解為去除400 Hz 以上頻率段的信號。

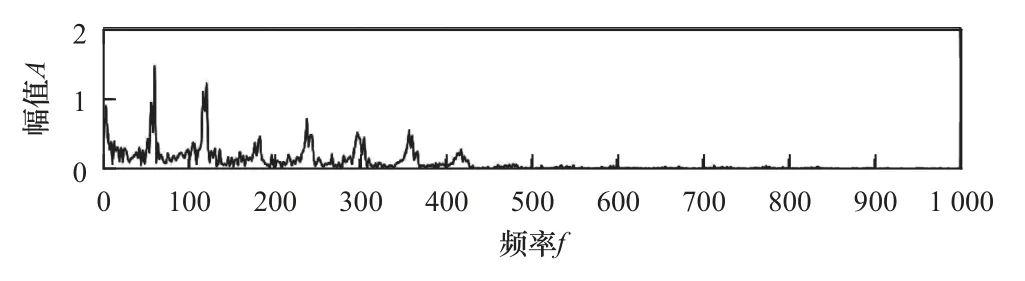
圖4 機床主軸振動信號過濾包絡譜

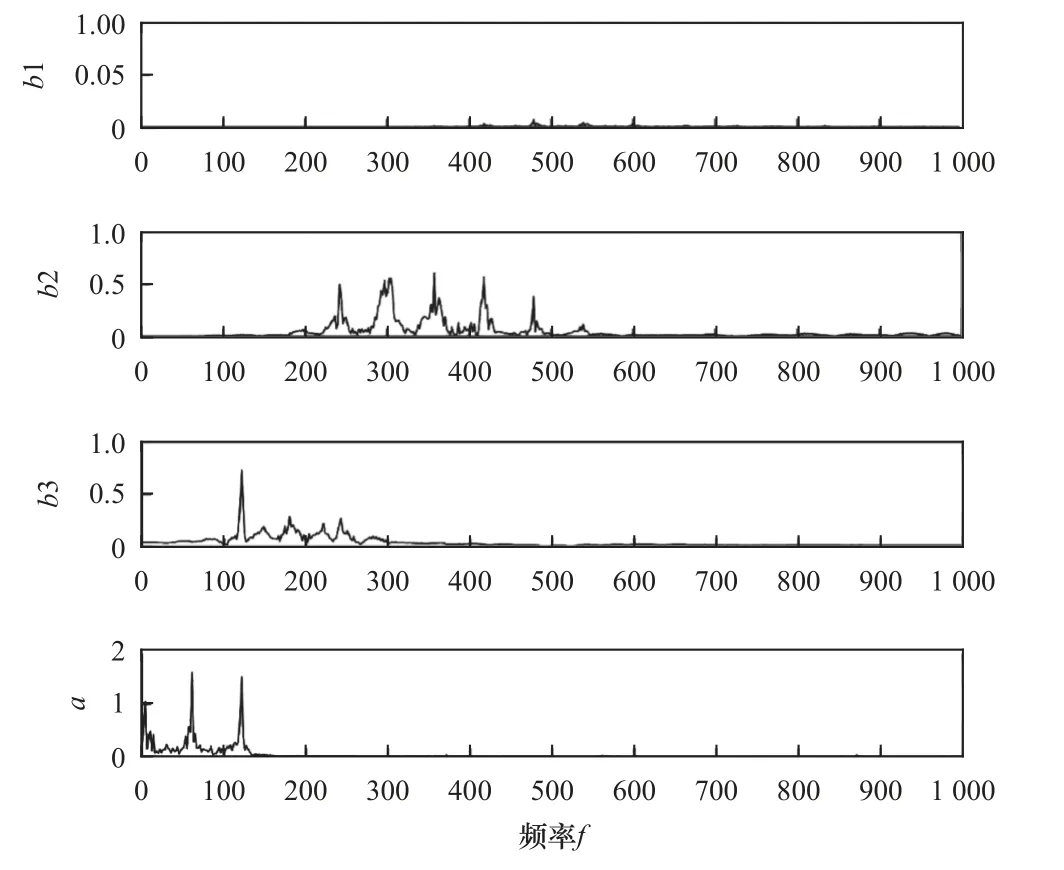
圖5 機床主軸振動信號分解圖

2.3 信號降噪結果分析

利用3 層譜圖小波方法實現(xiàn)機床主軸信號的轉換處理后，再以閾值數(shù)據(jù)過濾譜圖小波系數(shù)。由于滾齒加工過程具有斷續(xù)切削的特點，位于機床主軸振動信號間的信號以噪聲為主。與經(jīng)典小波閾值降噪方法進行比較，其中小波閾值降噪（wavelet threshold denoising，WTD），小波閾值收縮降噪（wavelet threshold shrinkage denoising， WTSD），小波包軟閾值降噪（wavelet packet soft-threshold denoising, WPSD）。圖6 給出了以本文方法和經(jīng)典時形成的時域圖。對比圖6a 和圖6b～圖6d 可以發(fā)現(xiàn)，位于SWTD 降噪周期中的過渡信號發(fā)生了顯著減弱，與初始信號發(fā)生周期性持續(xù)增強相比，更突出滾齒加工過程的斷續(xù)切削特征。在加工階段保持恒定的切削參數(shù)，機床對齒輪進行切削時周期性交變沖擊載荷也處于恒定狀態(tài)，由此形成穩(wěn)定的振動響應，也可以根據(jù)圖3 初始主軸振動信號進行判斷。完成降噪后，SWTD 降噪信號形成了穩(wěn)定幅值，已經(jīng)接近初始信號；WTD、WTSD 與WPSD 降噪信號則發(fā)生了幅值的大幅波動，造成時域數(shù)據(jù)丟失的結果，將其標注于圖6b～圖6d 的橢圓區(qū)域內(nèi)。SWTD 降噪信號可以獲得4.03 dB 的信噪比，相對WTD、WTSD 與WPSD 具備更高信噪比。根據(jù)以上分析可知，采用本文方法有效去除機床主軸振動信號噪聲，相對圖6b～圖6d 中的經(jīng)典小波閾值具備更優(yōu)降噪性能。

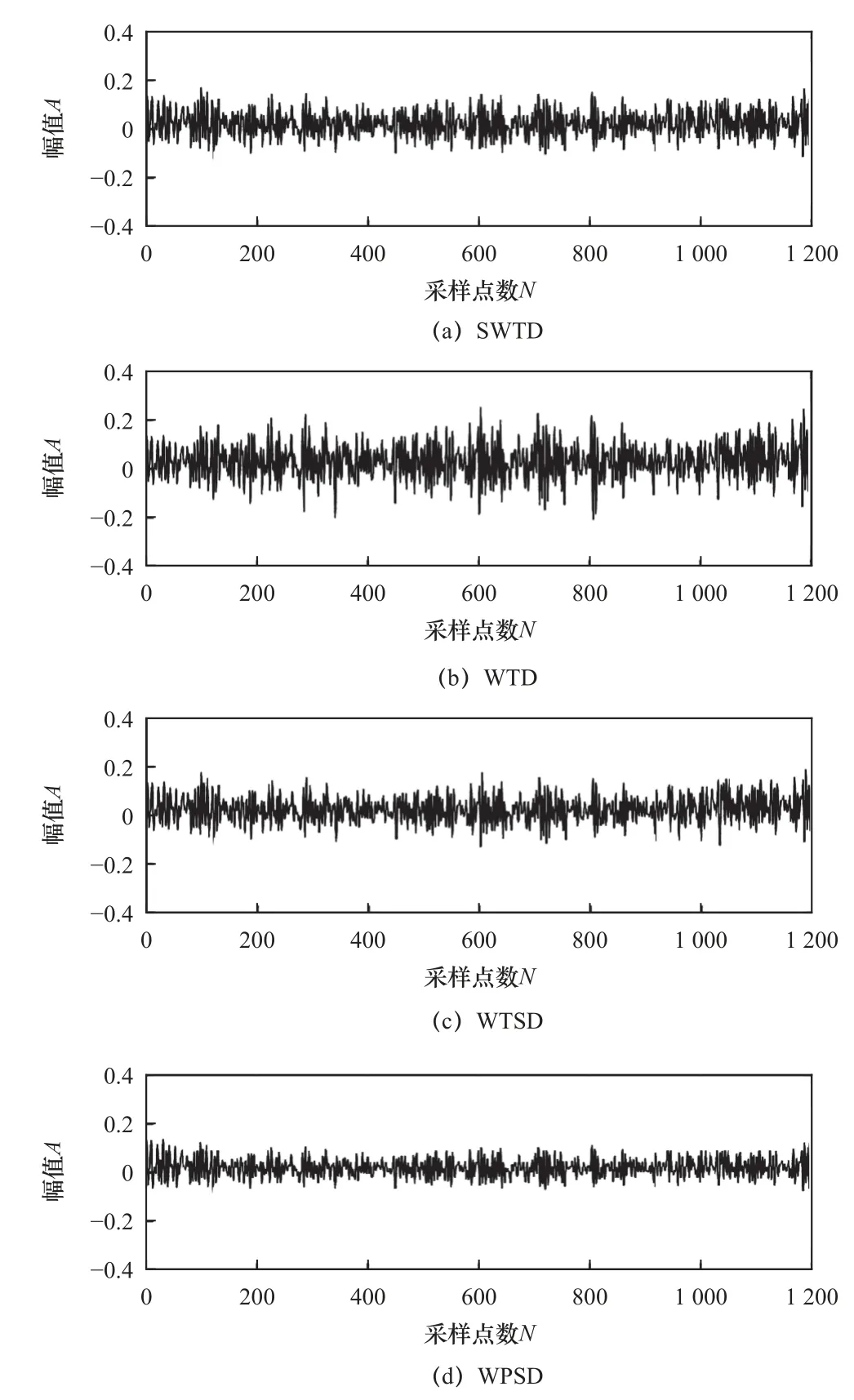
圖6 4 種SWTD、WTD、WTSD 與WPSD 方法降噪信號

對圖6 降噪信號開展包絡譜處理，結果如圖7a～圖7d 所示。結果顯示，圖7a 內(nèi)SWTD 包絡譜內(nèi)超過400 Hz 的高頻段已被消除，形成了由主軸自轉頻率與滾切頻率構成的主體成分，同時觀察到明顯的主軸自轉頻率特征，在滾切頻率中也形成了顯著的中心頻率，只形成了少量周邊干擾信號。對圖7b～圖7d 進行分析可以發(fā)現(xiàn)，WTD、WTSD 與WPSD降噪信號的包絡譜內(nèi)含有400 Hz 以上的噪聲頻率，基本分布于400～1 000 Hz 頻率段中，并未產(chǎn)生顯著的主軸自轉頻率特征，位于滾切頻率特征附近區(qū)域的干擾成分也較多。通過綜合分析可知，進行實際信號降噪處理時，本文方法相較于小波閾值降噪結果具備更優(yōu)性能。

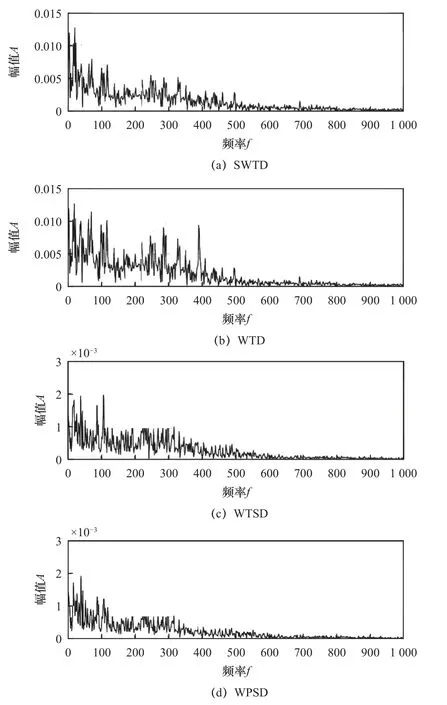
圖7 4 種SWTD、WTD、WTSD 與WPSD 方法降噪信號包絡譜圖

3 結語

本文開展基于譜圖小波閾值的機床主軸振動數(shù)字信號降噪研究，得到如下有益結果：

（1）機床主軸振動信號包含的有用頻率基本都處于400 Hz 范圍內(nèi)的低頻區(qū)，基本都是分布于400～1 000 Hz 頻率區(qū)內(nèi)。

（2）完成降噪后，SWTD 降噪信號形成了穩(wěn)定幅值，已經(jīng)接近初始信號，包絡譜內(nèi)超過400 Hz的高頻段已被消除，形成了由主軸自轉頻率與滾切頻率構成的主體成分，觀察到明顯主軸自轉頻率特征，表明本文方法相對小波閾值降噪結果具備更優(yōu)性能。