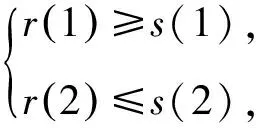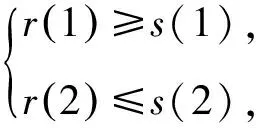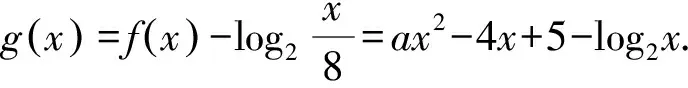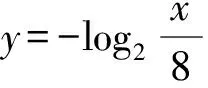對一道高三質量檢測題錯解的剖析與思考

鄭 良

(安徽省合肥市第四中學,安徽 合肥 230000)

皮亞杰說過:“錯誤是有意義的學習所必不可少的.”當代科學家、哲學家波普爾認為:“錯誤中往往孕育著比正確更豐富的發現和創造因素.”教學活動中學生的錯解展現了學生的思維活動過程,是教師了解學情的重要途徑.教師命題中也可能會出現“正題錯解”(正確的試題和錯誤的解析),洞悉“不露痕跡”的錯解需要解題者具有良好的數學素養,如對相關概念、關系、結構有明確的認識和理解,對解答過程中各步驟有清晰的邏輯分析等.

1 試題呈現

例1 (2021-2022學年度福州市高三期末質量檢測數學試題第19題)記ΔABC的內角A,B,C的對邊分別為a,b,c．已知c=acosB+ccosA．

(1)試判斷ΔABC的形狀,并說明理由;

2 解答呈現

對于第(1)小題,參考答案分別從正弦定理、余弦定理入手,得出結論:ΔABC為(A為頂角的)等腰三角形或(A為直角的)直角三角形,此處略.對于第(2)小題,參考答案給出兩種解法:

又因為sin∠ADB=sin∠ABC,

所以sin(π-∠ADB)=sin∠C.

即sin∠BDC=sin∠C.故∠BDC=∠C.

所以∠A=∠DBC.

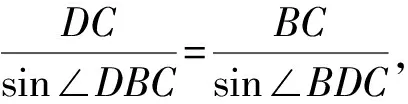
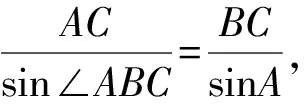
兩式相乘,得AC·DC=BC2(也可通過△ABC∽△BDC得到AC·DC=BC2).

又CD=AC-AD=AC-BC,

所以b(b-a)=a2,

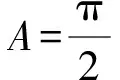
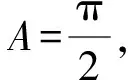
又因為sin∠ADB=sin∠ABC,

所以sin(π-∠ADB)=sin∠C.

即sin∠BDC=sin∠C.故∠BDC=∠C

所以∠A=∠DBC.

又因為AD=BD,所以∠A=∠DBA.

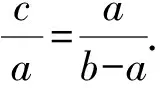
3 問題剖析

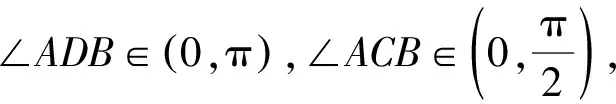
通過對特殊情況的補充,完善了解法1與解法2.為什么會出現漏解呢?命題人借助形的直觀,默認畫出的圖形(圖形的一般情形)為全部狀態,遺漏了特殊情形,出現了形的誤導.通過數的精準凸顯理性思維,將sin∠ADB=sin∠ABC等量代換得sin∠ADB=sin∠ACB,將目標由遠及近(由B?AC到D∈AC),結合∠ADB,∠ACB的范圍及條件“點D在邊AC上”對點D的位置進行確認.若命題者強化對“三角形的邊”概念的推敲,也能避免上述錯解.因此,在數學學習中一定要加強數學語言敘述的嚴謹性;在數學解題中一定要深化對條件的理解,確保所求結論的等價性.

4 其它解法

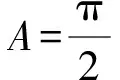
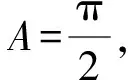
又因為sin∠ADB=sin∠ABC,

所以sin∠ADB=sin∠ACB.

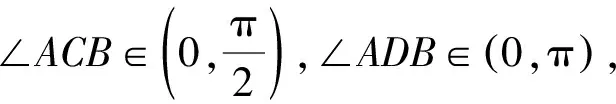
所以∠ADB=∠ACB或π-∠ADB=∠C.

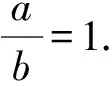
當點D與點C不重合時,由AD=BD=BC=a,記∠BAC=α,則∠ABD=α.

所以∠BDC=∠BCD=2α.

由b=c,可知∠ABC=∠BCD=2α.

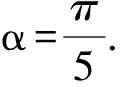
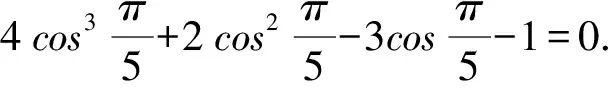
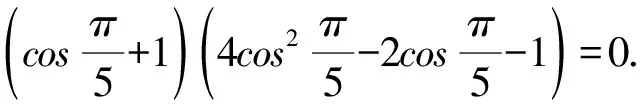
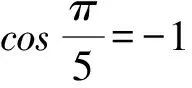
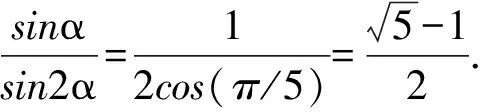
故由(1)可得B=C.

由sin∠ADB=sin∠ABC=sin∠ACB,得

∠ADB=∠ACB或∠ADB=π-∠ACB.

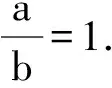
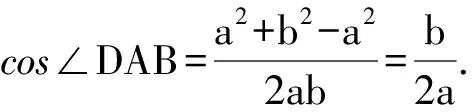
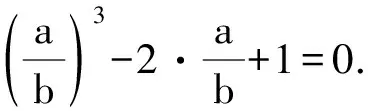
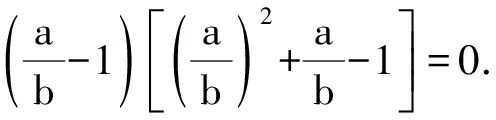
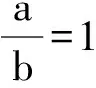
5 類似問題鏈接

例2已知平面向量a,b滿足a·b=0,|a-b|=2,則3|a|+2|b|的值可能是( ).

解析由已知可得|a-b|2=|a|2+|b|2=4.

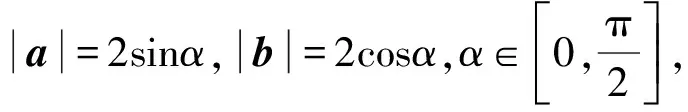
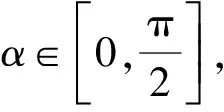
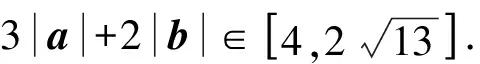
故選BC.

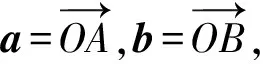
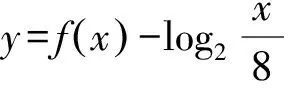
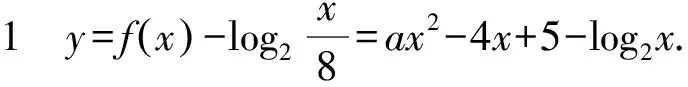
當a=0時,r(x)=-4x+5在[1,2]內單調遞減,s(x)=log2x在[1,2]內單調遞增,且r(1)=1>s(1)=0,r(2)=-3

所以-1≤a<0.

所以0

綜上所述,實數a的取值范圍為[-1,1].

綜上所述,當a≤1時,g(x)在[1,2]內單調遞減.

解得-1≤a≤1.

所以實數a的取值范圍為[-1,1].

類似的問題還有很多,如集合中的空集,區間的開閉對參數取值范圍的影響,“非零向量a與b的夾角為銳角”等價于“a·b>0且a與b不同向”等,請讀者自行整理.學生只有在平時的學習中弄清楚各個定理、性質的內容、條件和適用范圍,遇到相關問題時才不會望文生義,通過審題敏銳地發現題目中關鍵詞、情境等變化.存在錯解的數學問題往往觸及學生的知識盲區或能力不足之處,此類問題是學情的“晴雨表”,是教師珍貴的教學資料和備課素材. 對于此類問題,教師應當抓住教學契機,引領學生深刻剖析錯誤根源,引導學生有邏輯地思考問題,把握事物之間的關聯,形成重論據、有條理、合乎邏輯的思維品質和理性精神[1].面對錯解,教與學時不能簡單地采取直接糾正的方式,還要弄清楚錯解產生的深層次原因,努力扭轉學生解題“對號入座”的現象,深化對問題的理解,切實提高學生分析問題和解決問題的能力,遇到問題時才能以不變應萬變.