考慮有界場的幾何不確定性非概率可靠性拓撲優(yōu)化1)

戰(zhàn)俊杰 彭秀林 白仲航,?,2)

* (河北省健康人居環(huán)境重點實驗室,天津 300132)

? (河北工業(yè)大學國家技術(shù)創(chuàng)新方法與實施工具工程技術(shù)研究中心,天津 300401)

引言

拓撲優(yōu)化作為一種有效的自動化設(shè)計工具,已廣泛應(yīng)用于各種結(jié)構(gòu)的設(shè)計問題.常用的拓撲優(yōu)化方法主要包括SIMP (solid isotropic material with penalization)法[1-2]、ESO (evolutionary structural optimization)法[3]、水平集法[4-5]、智能拓撲優(yōu)化方法[6-7]等.此外,Guo 等[8-12]提出了一種基于移動可變形組件/孔洞的拓撲方法,以可移動可變形組件為基本元件進行結(jié)構(gòu)拓撲優(yōu)化設(shè)計.近期,Luo 等[13-16]提出了一種基于材料場級數(shù)展開 (material-field series-expansion,MFSE)的拓撲優(yōu)化方法,該方法能夠有效避免結(jié)構(gòu)中的棋盤格現(xiàn)象及網(wǎng)格依賴性問題,并且能夠大幅減少設(shè)計變量個數(shù),提高計算效率.

在結(jié)構(gòu)的加工制造及使用過程中,不可避免會存在各種不確定性,比如加工誤差導(dǎo)致的幾何不確定性,工作時的載荷不確定性等.這些不確定性會使結(jié)構(gòu)產(chǎn)生性能波動和關(guān)鍵指標降低,嚴重影響結(jié)構(gòu)的安全性.現(xiàn)有處理不確定性的方法主要是基于概率框架進行的.隨著概率可靠性優(yōu)化方法的發(fā)展,一些實用的求解策略如功能度量法[17-18],序列優(yōu)化方法[19]及概率神經(jīng)網(wǎng)絡(luò)[20]等都極大地促進了概率可靠性方法在實際工程中的應(yīng)用.此外,實際工程中的許多不確定性,如分布荷載、幾何尺寸、材料屬性等,其在空間不同位置上的實現(xiàn)是隨空間位置的變化而變化的,這屬于“不確定場”問題.目前,常用來描述不確定場的模型為隨機場模型[21-23].將制造誤差引起的幾何缺陷描述為隨機閾值場模型,Kang 等[22]提出了一種考慮幾何空間不確定性的概率可靠性拓撲優(yōu)化方法.通過將非侵入式PCE (the polynomial chaos expansion) 方法與設(shè)計靈敏度分析相結(jié)合,Keshavarzzadeh 等[23]提出了一種隨機場幾何不確定性下的可靠性拓撲優(yōu)化的系統(tǒng)方法.

針對工程實際中廣泛存在的未知但有界不確定性,由于缺少大量樣本數(shù)據(jù)信息,難以獲得不確定性準確地概率分布特征,因此概率不確定性理論不再適用.作為概率可靠性理論的有效補充,研究人員提出了許多描述參數(shù)不確定性的非概率模型,比如模糊模型[24-25]、證據(jù)理論[26-27]、區(qū)間模型及凸模型[28-34]等.Sofi 等[30]通過結(jié)合區(qū)間運算和安全系數(shù)方法,將非概率可靠性指標描述為一個區(qū)間變量.Pantelides等[33]提出了一種反優(yōu)化技術(shù)進行考慮載荷不確定性的非概率可靠性的優(yōu)化設(shè)計.將結(jié)構(gòu)邊界長度變化描述為凸模型,Luo 等[34]完成了考慮結(jié)構(gòu)幾何不確定性的非概率可靠性優(yōu)化設(shè)計,優(yōu)化后的結(jié)構(gòu)具有更高的可靠性.

至于少樣本的場不確定性問題,由于樣本數(shù)量有限,因此隨機場模型也不再適用.通過引入EUI(external unit interval)變量,Muscolino 等[35-36]提出了一種區(qū)間場方法來量化未知但有界的不確定場.基于空間相關(guān)性的數(shù)學定義和非概率級數(shù)展開方法,Luo 等[37]提出了一種處理有限樣本下不確定場問題的有界場模型.基于有界場模型,Zhan 等[38]提出了一種非概率可靠性指標進行結(jié)構(gòu)場不確定性下的非概率可靠性評估,并進一步完成了不確定載荷場作用下的結(jié)構(gòu)非概率可靠性優(yōu)化設(shè)計研究[39].

文獻調(diào)研顯示,盡管基于參數(shù)的非概率可靠性優(yōu)化方法已應(yīng)用于結(jié)構(gòu)幾何不確定性分析,但針對工程實際中考慮少樣本及空間變化特性的幾何不確定性,仍缺乏合理的可靠性優(yōu)化模型.因此,本文將采用閾值技術(shù)[40]進行具有空間變化特性的幾何不確定性表征,并將Heaviside 過濾函數(shù)中的閾值 η 假定為有界不確定閾值場,建立非概率有界場模型,進而完成考慮結(jié)構(gòu)幾何不確定性的非概率可靠性拓撲優(yōu)化設(shè)計.

本文的具體安排如下: 首先進行不確定場的非概率描述,即將不確定場描述為非概率有界場模型;第2 節(jié)進行結(jié)構(gòu)幾何不確定性的描述,即通過不確定閾值場來表示,進而描述為有界場模型;第3 節(jié)為建立結(jié)構(gòu)的非概率可靠性優(yōu)化模型;在第4 節(jié)推導(dǎo)了模型的靈敏度信息,并采用移動漸近線法 (method of moving asymptotes)[41]求解優(yōu)化問題;最后通過2 個數(shù)值算例驗證了模型的有效性.

1 不確定場的非概率描述

其中Z0(x) 為標準化的不確定場,且滿足-1 ≤Z0(x)≤1.

考慮到在實際工程中結(jié)構(gòu)的不確定邊界是連續(xù)變化的,因此假定有界不確定場Z(x) 的空間波動具有一定相關(guān)性.在本文中,設(shè)計域 Ωdom內(nèi)任意兩個觀察點xa和xb對應(yīng)的不確定場的相關(guān)性通過相關(guān)函數(shù)R(xa,xb) 來描述,R(xa,xb) 的表達式為

其中,符號 ‖·‖表示2 范數(shù).L是不確定場Z(x) 的相關(guān)長度,它用來控制不確定場的空間波動程度.當相關(guān)長度L較小時,不確定場的空間波動較為劇烈,L=0表示所有觀察點處的變量都是不相關(guān)的;當相關(guān)長度L較大時,波動較為平緩,L→+∞ 表示不確定場完全相關(guān),即所有觀察點處的不確定場值Z(xi) 均相等.

設(shè)計域內(nèi)各觀察點之間的相關(guān)性構(gòu)成了相關(guān)矩陣R,因此R表示為

基于非概率級數(shù)擴展,標準化的不確定場Z0(x)可表示為

在式(4)中,特征值 λj為降序排列,特征值越小的項對不確定場的貢獻值越小.因此,為提高模型的計算效率,可對式(4)進行截斷,僅保留前M項,即通過M個不確定系數(shù)(ξj(j=1,2,···,M))來描述不確定場.截斷公式可表示為

其中,α 是一個很小的值.在本文中,α=1.0×10-6.

對式(4)進行截斷后并代入式(1)中,可得到不確定場的表達式為

已知標準化的不確定場Z0(x) 的變化范圍為Z0(x)∈[-1,1],得

對式(7) 兩邊平方,并寫成向量的形式,可以得到

2 幾何不確定性的描述

在現(xiàn)有的拓撲優(yōu)化設(shè)計中,Heaviside 過濾技術(shù)已得到了廣泛的應(yīng)用.與敏度法和密度法過濾相比,優(yōu)化的結(jié)構(gòu)經(jīng)Heaviside 過濾可獲得清晰的結(jié)構(gòu)邊界.本文用到的Heaviside 過濾函數(shù)定義為

其中,不確定系數(shù) ξj的變化范圍如式(9)所示.

為了進一步說明不確定閾值場 η (x) 對結(jié)構(gòu)不確定性的影響,圖2 以MBB 梁為例分別給出了不確定閾值場 η (x) 和確定閾值 η (x)≡0.5 對結(jié)構(gòu)邊界的影響.從圖2 中可以看出,與閾值為恒定值(η (x)≡0.5)相比,當閾值描述為不確定場時,結(jié)構(gòu)的邊界會存在一定的擾動(認為是幾何不確定性).

3 考慮幾何不確定的結(jié)構(gòu)非概率可靠性拓撲優(yōu)化模型

3.1 考慮不確定閾值場的結(jié)構(gòu)非概率可靠性指標

正如第2 節(jié)描述的那樣,不確定閾值場 η (x) 會對結(jié)構(gòu)的邊界產(chǎn)生影響,進而影響結(jié)構(gòu)的性能.因此,結(jié)構(gòu)性能可表示為不確定閾值場 η (x) 的函數(shù).在本文中,結(jié)構(gòu)的性能函數(shù)可表示為C(η)≤C*,其中C為結(jié)構(gòu)的柔順性,C*為給定的柔順性約束.令g(η)=C*-C(η),則g(η) 稱為極限狀態(tài)函數(shù).

由式(6)可知,不確定閾值場 η (x) 是關(guān)于不確定系數(shù) ξ 的函數(shù).因此,在不確定系數(shù) ξ 的空間中,極限狀態(tài)函數(shù)g(η) 可進一步表示為G(ξ)=g(η(ξ,x)).

依據(jù)有界不確定場的非概率可靠性指標的定義[39],極限狀態(tài)函數(shù)G(ξ) 可將不確定系數(shù) ξ 空間劃分為可靠區(qū)和失效區(qū),如圖3 所示(為便于表示,示意圖中只考慮了2 個不確定性系數(shù) ξ1和 ξ2).因此,考慮幾何不確定性的結(jié)構(gòu)非概率可靠性指標定義為

即表示在可靠區(qū)域內(nèi)所允許的最大不確定性.其中,式(11)的最優(yōu)解 β*為非概率可靠性指標.jud(G(0))用來判斷可靠性指標 β*的正負,具體的表達式為

3.2 基于MFSE 模型的拓撲優(yōu)化方法

為避免傳統(tǒng)密度法拓撲優(yōu)化中的棋盤格現(xiàn)象及網(wǎng)格依賴性問題,本文將采用基于MFSE 的拓撲優(yōu)化方法[13].在本方法中,結(jié)構(gòu)拓撲通過一個具有一定空間相關(guān)性的有界材料場函數(shù)φ(y)∈[-1,1],y∈Ωdom來描述.經(jīng)材料場級數(shù)展開,并進行截斷保留前Me(Me≤N)項,則場函數(shù) φ (y) 可表示為

其中,κk和 ψk為相關(guān)矩陣 Γ 的特征值和特征向量.相關(guān)矩陣 Γ 的表達式為

類似于前面不確定場的處理方式,依據(jù)有界不確定場函數(shù) φ (y)∈[-1,1] 的界限并引入符號Hm=κ-1/2ΨTΓD(ym)ΓD(ym)TΨκ-1/2,則式(13) 可轉(zhuǎn)化為如下形式

在本方法中,假定結(jié)構(gòu)的單元中心與不確定場函數(shù) φ (y) 的觀察點ym一一對應(yīng).單元的插值函數(shù)可表示為

基于MFSE 的結(jié)構(gòu)柔順性拓撲優(yōu)化問題可表示為

3.3 結(jié)構(gòu)非概率可靠性優(yōu)化模型

在本文中,結(jié)合MFSE 優(yōu)化模型(式(17))及考慮不確定場的可靠性指標(式(11)),考慮結(jié)構(gòu)幾何不確定性的非概率可靠性拓撲優(yōu)化問題可表示為:在結(jié)構(gòu)體積一定的情況下使結(jié)構(gòu)的可靠性指標最大化,進而來提高結(jié)構(gòu)的可靠性,優(yōu)化列式如下所示

需要注意的是,在式(18)的外層優(yōu)化中,很難準確地獲得可靠性指標 β*對設(shè)計變量χ的靈敏度信息.因此,可采用關(guān)心性能法[34,39]對式(18)進行等效變換.基于關(guān)心性能法(詳見文獻[34,39]),式(18)的非概率可靠性拓撲優(yōu)化問題可以轉(zhuǎn)化為

其中,內(nèi)層優(yōu)化為獲得在外層設(shè)計變量為χ時的關(guān)心性能值 σ (χ,ξ*),ξ*稱為關(guān)心點.確定了關(guān)心點 ξ*后便可得到此時對應(yīng)的不確定閾值場 η (x) (依據(jù)式(11))分布情況.極限狀態(tài)函數(shù)G(χ,ξ) 是結(jié)構(gòu)柔順性的函數(shù),表示為G(χ,ξ)=C*-C(χ,ξ).由于C*為一給定常數(shù),因此式(19)中外層優(yōu)化的目標函數(shù)maxG(χ,ξ*)可等效表示為 m inC(χ,ξ*);內(nèi)層優(yōu)化等效為 maxC(χ,ξ).為給定的非概率可靠性指標下限值.

本文采用移動漸近線方法(MMA)[41]求解該非概率可靠性優(yōu)化問題.優(yōu)化模型的收斂準則定義為變量(內(nèi)層為變量 ξ,外層為變量χ)在相鄰兩步迭代中的最大變化值小于0.01.

4 靈敏度分析

4.1 極限狀態(tài)函數(shù)對不確定系數(shù)的靈敏度分析

本文考慮幾何不確定性的非概率可靠性優(yōu)化問題是基于梯度算法求解的,因此靈敏度分析是必不可少的過程.該優(yōu)化模型(式(19))為嵌套優(yōu)化,首先求解內(nèi)層優(yōu)化的靈敏度信息,即極限狀態(tài)函數(shù)G(χ,ξ) 對不確定系數(shù) ξj的靈敏度分析.具體求解過程如下所示

平衡方程Ku=F兩邊對不確定閾值場 η (xi) 求導(dǎo),并等式變換,得

4.2 關(guān)心性能值對設(shè)計變量的靈敏度分析

優(yōu)化模型中外層優(yōu)化主要涉及的靈敏度為關(guān)心性能值 σ 對設(shè)計變量χk的靈敏度分析,為實現(xiàn)優(yōu)化模型的解耦,假設(shè)關(guān)心性能點 ξ 對設(shè)計變量的靈敏度為0.因此,其表達式為

其中,關(guān)心性能點 ξ*為優(yōu)化模型內(nèi)層的最優(yōu)解.

依據(jù)鏈式法則,式(24)表示為

引入伴隨向量 γ,式(27)表示為

依據(jù)式(16)的插值函數(shù),可得到

在單元層面上,關(guān)心性能值 σ 對設(shè)計變量χk的靈敏度可表示為

4.3 非概率可靠性拓撲優(yōu)化流程圖

為便于理解式(19)的非概率可靠性拓撲優(yōu)化模型,圖4 給出了優(yōu)化過程的流程圖.優(yōu)化過程為嵌套優(yōu)化,其中右側(cè)為內(nèi)層優(yōu)化,目的是得到在幾何不確定性下的關(guān)心性能值,求解過程涉及極限狀態(tài)函數(shù)G(χ,ξ) 對不確定系數(shù) ξj的靈敏度分析(第4.1 節(jié)內(nèi)容);左側(cè)為外層優(yōu)化,即在給定體積約束下獲得結(jié)構(gòu)的最優(yōu)拓撲,求解過程涉及關(guān)心性能值G(χ,ξ*) 對設(shè)計變量χk的靈敏度分析(第4.2 節(jié)內(nèi)容).

5 數(shù)值算例

本節(jié)給出了2 個數(shù)值算例來驗證本文提出的考慮幾何不確定性的非概率可靠性優(yōu)化模型的有效性.對于這2 個算例,結(jié)構(gòu)的彈性模量和泊松比分別為E0=2.0×105MPa 和υ=0.3.在整個優(yōu)化過程中,結(jié)構(gòu)始終處于線彈性階段.這2 個算例都是Windows 10 操作系統(tǒng)性下基于MATLAB 軟件計算的,電腦的配置為AMD Ryzen Threadripper PRO 5965 WX 24-Cores 3.80 GHz,128 GB RAM.

5.1 MBB 梁結(jié)構(gòu)的非概率可靠性優(yōu)化

如圖5 所示為半個MBB 梁結(jié)構(gòu),結(jié)構(gòu)的尺寸為140 mm×70 mm,整個設(shè)計域離散為140×70(9800)個平面應(yīng)力單元.結(jié)構(gòu)右下角約束了Y方向的位移,左邊約束了X方向的位移.集中載荷F=100 N 垂直作用于結(jié)構(gòu)的左上角,方向為-Y方向.不確定閾值場的范圍為 η (x)∈[0.25,0.75],在本算例中考慮了不確定閾值場2 種不同的相關(guān)長度,即L=80 mm 和L=30 mm.此外,還討論了2 種不同的可靠性指標約束(=1.0 和=1.5)對拓撲結(jié)構(gòu)的影響.本算例給定的結(jié)構(gòu)體積分數(shù)為f=50%.

作為對比,首先給出了本算例的確定性優(yōu)化結(jié)果,即不確定閾值場 η (x)≡0.5 的情況(等價于相關(guān)長度L→+∞ 時的閾值場),優(yōu)化結(jié)果如圖6 所示.考慮不確定閾值場的結(jié)構(gòu)非概率可靠性拓撲優(yōu)化結(jié)果如圖7 所示.通過對比非概率可靠性優(yōu)化結(jié)果(圖7 左列)與確定性優(yōu)化結(jié)果(圖6),可以看出非概率可靠性優(yōu)化的最優(yōu)拓撲構(gòu)型與確定性優(yōu)化的不同,并且非概率可靠性優(yōu)化的最優(yōu)解是通過增加更多的肋來保證結(jié)構(gòu)在不確定閾值場下的可靠性.

此外,圖7(a)和圖7(b)為考慮了不確定閾值場η(x)相 同的相關(guān)長度(L=80 mm),但優(yōu)化模型(式(19))的可靠性指標約束值不同(=1.0 和=1.5).對比這兩個工況,可以看出非概率可靠性拓撲優(yōu)化結(jié)果存在一定差異(如圖7(a)和圖7(b)左列),即結(jié)構(gòu)中的“桿件”數(shù)量和位置存在明顯不同.另外,當 β 不同時,盡管關(guān)心點處的不確定閾值場空間分布波動情況類似,但不確定場 η (x) 的空間波動范圍會隨著可靠性指標約束值的增大而增大: (1)=1.0 時,波動范圍是 [ 0.34,0.75] (如圖7(a)右列);(2)=1.5 時,波動范圍是 [ 0.19,0.87] (如圖7(b)右列).優(yōu)化結(jié)果存在差異的原因在于,隨著可靠性指標約束值的增加,進行結(jié)構(gòu)的可靠性設(shè)計時考慮的幾何不確定性范圍更大,關(guān)心點處不確定閾值場的波動范圍也會更大(如圖7(a)和圖7(b)右列).同時,由于考慮了更多的不確定性,那么設(shè)計的結(jié)構(gòu)可靠性會更高,最優(yōu)的拓撲構(gòu)型也會相應(yīng)地發(fā)生變化(如圖7(a)和圖7(b)左列).此外,不確定閾值場 η (x) 的分布特點基本滿足在結(jié)構(gòu)左側(cè)區(qū)域數(shù)值較大,右側(cè)區(qū)域數(shù)值較小的特點.

不同情況下的考慮幾何不確定性的非概率可靠性優(yōu)化模型計算時間如表1 所示.其中,內(nèi)層優(yōu)化和外層優(yōu)化的計算時間均為迭代一次的平均時間,內(nèi)層優(yōu)化的迭代步數(shù)為30 步左右,外層優(yōu)化迭代為150 步左右.從表1 中可以看出,當不確定閾值場的相關(guān)長度較小(L=30 mm)時,內(nèi)層優(yōu)化需要的時間更長(23.360 4 s).這是因為當相關(guān)長度較小時,則需要更多的截斷項才能保證要求的不確定場截斷精度(式(5)),那么式(19)中內(nèi)層優(yōu)化中的變量數(shù)(ξj)會更多,計算時間也會相應(yīng)地增加.

表1 不同情況下非概率可靠性優(yōu)化模型計算時間Table 1 The computing time of non-probability reliabilitybased topology for different cases

為了說明優(yōu)化結(jié)果的正確性,我們將通過差分靈敏度分析法來驗證第4 節(jié)的解析靈敏度分析的正確性,差分法采用的差分步長為0.001.以L=80 mm,=1.0的工況為例,內(nèi)層優(yōu)化共包含25 個不確定系數(shù) ξj(j=1,2,···,25),隨機選取4 個不確定系數(shù)(ξ2,ξ5,ξ10,ξ15) 進行靈敏度對比,對比結(jié)果如表2 所示.外層優(yōu)化同樣隨機選取4 個設(shè)計變量(χ2,χ10,χ30,χ70),對比結(jié)果如表3 所示.

表2 內(nèi)層優(yōu)化中不確定系數(shù)的靈敏度Table 2 Sensitivity of uncertainty coefficients in inner-loop optimization

表3 外層優(yōu)化中設(shè)計變量的靈敏度Table 3 Sensitivity of design variables in outer-loop optimization

從表2 和表3 的對比結(jié)果中可以看出,第4 節(jié)的解析靈敏度和差分法的靈敏度計算結(jié)果非常相近,其相對誤差均在 1%以內(nèi).這證明了本文優(yōu)化模型及解析靈敏度推導(dǎo)的正確性.

基于本文提出的考慮結(jié)構(gòu)幾何不確定性的非概率可靠性拓撲優(yōu)化模型,本算例中不同工況下的內(nèi)層優(yōu)化和外層的優(yōu)化迭代歷史分別如圖8,圖9 所示.其中,圖8 表示第一次的內(nèi)層優(yōu)化.從圖8 中可以看出,在整個內(nèi)層優(yōu)化的過程中,目標函數(shù)都能夠快速收斂到某一特定值(圖8 實線所示),并且結(jié)構(gòu)能夠始終滿足指定的可靠性指標約束(圖8 虛線所示).此外,圖9 的外層優(yōu)化迭代歷史也體現(xiàn)了優(yōu)化模型穩(wěn)定的收斂性.因此,這也進一步證明了采用梯度優(yōu)化算法來求解本文提出的非概率可靠性優(yōu)化模型是合理有效的.

為了進一步驗證非概率可靠性拓撲優(yōu)化結(jié)果的合理性,我們將非概率可靠性拓撲優(yōu)化關(guān)心點ξ*(式19)處的幾何不確定性(即表示為圖7 右列的不確定閾值場)施加到確定性拓撲優(yōu)化結(jié)構(gòu)(圖6 所示)和可靠性拓撲優(yōu)化結(jié)構(gòu)(圖7 左列)上,來進行結(jié)構(gòu)的柔順性對比,對比結(jié)果如表4 所示.以L=80 mm;=1.0的非概率可靠性拓撲優(yōu)化結(jié)構(gòu)為例(如表4第2,3 列所示),當確定性優(yōu)化結(jié)構(gòu)中存在幾何不確定性時(即關(guān)心點 ξ*處的不確定閾值場),結(jié)構(gòu)柔順性值為C=34.95 N·mm,大于可靠性拓撲優(yōu)化結(jié)構(gòu)在該關(guān)心點 ξ*處的柔順性值C=33.66 N·mm.此外,其他條件下的非概率可靠性拓撲優(yōu)化結(jié)構(gòu)同樣滿足這種情況: (1)L=80 mm,=1.5 時,如表4 第4,5 列所示,C=35.57 N·mm 和C=34.94 N·mm;(2)L=30 mm,=1.0 時,如表4 第6,7 列所示,C=38.78 N·mm 和C=34.87 N·mm.因此,通過上述對比可以看出,當存在幾何不確定性時,考慮幾何不確定性的非概率可靠性優(yōu)化結(jié)構(gòu)具有更好的抵抗幾何不確定性的能力,即有更小的結(jié)構(gòu)柔順性.

表4 可靠性拓撲優(yōu)化結(jié)構(gòu)和確定性優(yōu)化結(jié)構(gòu)在關(guān)心點 ξ* 處的柔順性對比Table 4 Comparison of compliance between reliability-based and deterministic topology optimization structures at concerned point ξ*

5.2 懸臂梁結(jié)構(gòu)的非概率可靠性優(yōu)化

在本算例中,以懸臂梁結(jié)構(gòu)為例,如圖10 所示,懸臂梁結(jié)構(gòu)設(shè)計域的尺寸為 1 12 mm×70 mm,離散為 7 840 (112×70) 個單元.懸臂梁結(jié)構(gòu)的左側(cè)完全約束,集中力F=100 N 作用于結(jié)構(gòu)的右下角,方向為-Y方向.不確定閾值場的變化范圍為 η(x)∈[0.25,0.75].結(jié)構(gòu)的體積分數(shù)約束同樣設(shè)定為f=50%.本算例考慮了一種不確定閾值場的相關(guān)長度L=30 mm 和一種可靠性指標約束值=1.0 來進行考慮幾何不確定性的結(jié)構(gòu)非概率可靠性優(yōu)化設(shè)計.

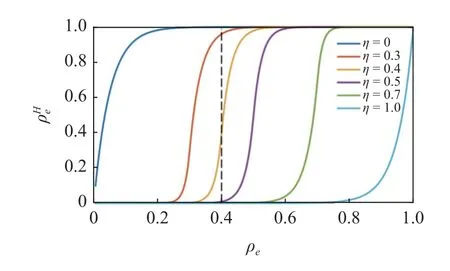
圖1 光滑系數(shù) δ=20 時,不同閾值 η 下Heaviside 函數(shù)Fig.1 The Heaviside function under different thresholds η when smoothing parameterδ=20

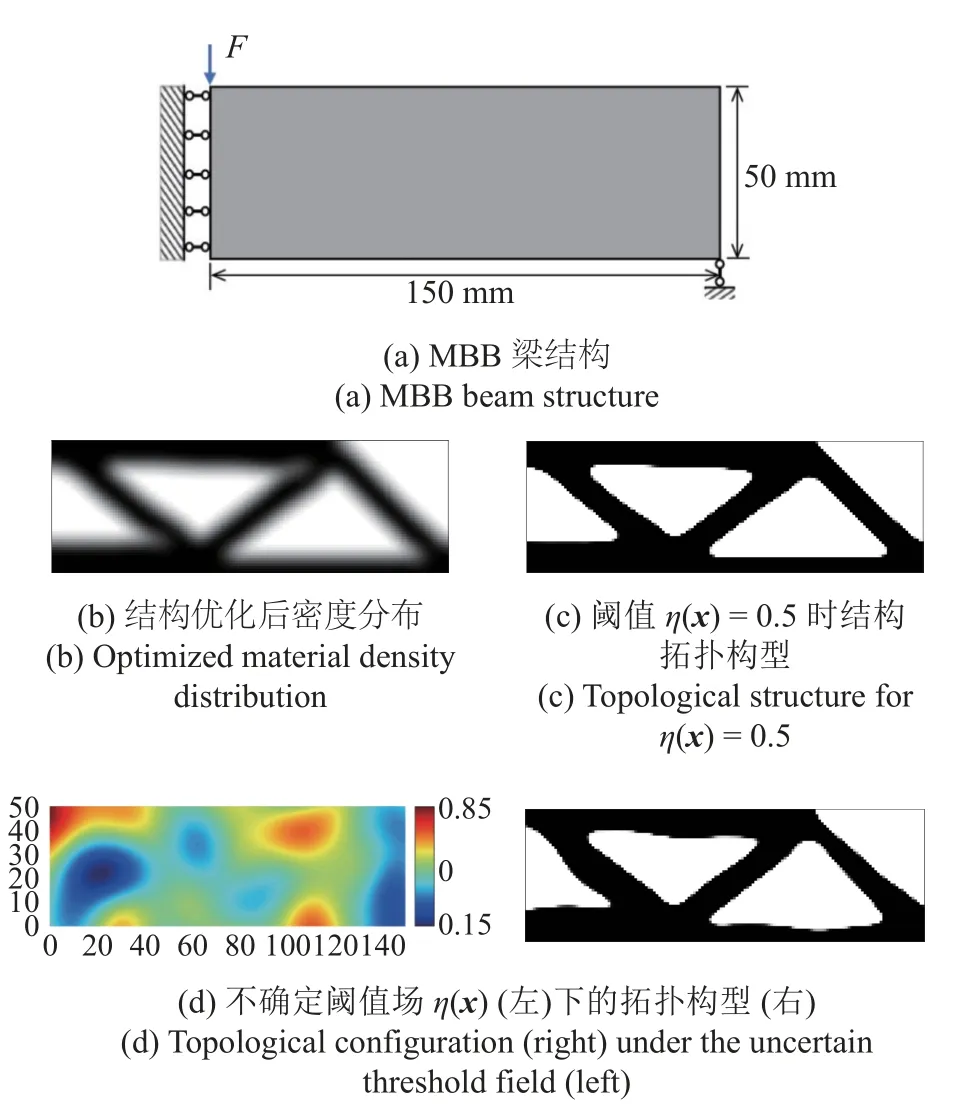
圖2 閾值為定值(η (x)≡0.5)及不確定閾值場 η (x) 下的MBB 梁拓撲構(gòu)型Fig.2 Topological structure of MBB beam considering the constant threshold η (x)≡0.5 and uncertain threshold field

圖3 有界場模型非概率可靠性指標示意圖Fig.3 Schematic diagram of non-probabilistic reliability index for the bounded field model

圖4 非概率可靠性拓撲優(yōu)化流程圖Fig.4 The flowchart of non-probabilistic reliability-based topology optimization

圖5 MBB 梁結(jié)構(gòu)設(shè)計域Fig.5 Design domain for the MBB beam structure

圖6 MBB 梁結(jié)構(gòu)確定性拓撲優(yōu)化結(jié)果(不確定閾值場 η (x)≡0.5),目標函數(shù)值C=34.22 N·mmFig.6 Deterministic topology optimization solution for the MBB beam structure (uncertain threshold field η (x)≡0.5) and the objective function valueC=34.22 N·mm

圖7 不同相關(guān)長度 L 及不同可靠性指標 約束下的非概率可靠性拓撲優(yōu)化結(jié)果(左列)和關(guān)心點處的不確定閾值場 η (x) 分布情況(右列)Fig.7 Non-probabilistic reliability-based topology optimization solution (left column) and the distribution of uncertain threshold fields at the concerned point (right column) with different correlation lengthL and non-probability reliability index

圖8 內(nèi)層優(yōu)化迭代歷史(實線表示目標函數(shù),虛線表示可靠性指標約束)Fig.8 Iteration history of inner-loop optimization (solid lines represent the objective function and dashed lines represent reliability index constraints)

圖9 確定性和非概率可靠性拓撲優(yōu)化的迭代歷史Fig.9 Iteration histories of the deterministic and non-probability reliability-based topology optimization

圖10 懸臂梁結(jié)構(gòu)設(shè)計域Fig.10 Design domain for the cantilever structure

作為對比,本算例中同樣進行了懸臂梁結(jié)構(gòu)的確定性拓撲優(yōu)化設(shè)計,在整個優(yōu)化過程中閾值場在設(shè)計域內(nèi)各點處的閾值均為恒定值,即 η (x)≡0.5,懸臂梁結(jié)構(gòu)的確定性拓撲優(yōu)化結(jié)果如圖11 所示.考慮不確定閾值場的結(jié)構(gòu)非概率可靠性拓撲優(yōu)化結(jié)果及關(guān)心點對應(yīng)的不確定閾值場分布情況如圖12 所示(L=40 mm,=1.0).對比2 個優(yōu)化結(jié)果可以看出,在材料體積一定的情況下,可靠性優(yōu)化設(shè)計的結(jié)構(gòu)產(chǎn)生了更多的肋來抵抗結(jié)構(gòu)中的幾何不確定性,以提高結(jié)構(gòu)的可靠性.本算例進一步證明了本文提出的考慮幾何不確定性的非概率可靠性優(yōu)化模型的有效性.

圖11 懸臂梁結(jié)構(gòu)確定性拓撲優(yōu)化結(jié)果(不確定閾值場 η (x)≡0.5),目標函數(shù)值C=19.62 N·mmFig.11 Deterministic topology optimization solution for the cantilever structure (uncertain threshold field η (x)≡0.5) and the objective function valueC=19.62 N·mm

圖12 相關(guān)長度 L=40 mm 及可靠性指標約束值 β=1.0 時的懸臂梁結(jié)構(gòu)非概率可靠性拓撲優(yōu)化結(jié)果和關(guān)心點處的閾值場分布,目標函數(shù)值C=19.79 N·mmFig.12 Non-probabilistic reliability-based topology optimization solution and the distribution of uncertain threshold fields at the concerned point with correlation length L=40 mm and non-probability reliability index β=1.0 and the objective function valueC=19.79 N·mm

6 結(jié)論

本文提出了一種考慮結(jié)構(gòu)幾何不確定性的非概率可靠性優(yōu)化模型,其中結(jié)構(gòu)的幾何不確定性通過有界不確定閾值場函數(shù)來表示.基于材料場級數(shù)展開,不確定閾值場可通過一組不確定系數(shù)來描述.優(yōu)化模型為嵌套優(yōu)化問題,內(nèi)層是進行結(jié)構(gòu)的可靠性評估,外層為確定結(jié)構(gòu)的最優(yōu)布局.本文采用了基于梯度的優(yōu)化算法來求解該非概率可靠性優(yōu)化模型.數(shù)值算例表明,采用本文提出的非概率可靠性優(yōu)化方法,可以得到分布更為合理的拓撲構(gòu)型來提高結(jié)構(gòu)在考慮幾何不確定性下的可靠性.