基于場路結合的微波加熱系統等效電路模型

楊彪，蘇森濤，馬亦驥，倪瑞璞，曾德明，肖青云，王銀雙

(1.昆明理工大學 信息工程與自動化學院，云南 昆明，650500；2.昆明理工大學 云南省人工智能重點實驗室，云南 昆明，650500；3.昆明理工大學 非常規冶金教育部重點實驗室，云南 昆明，650093)

微波加熱是一種新型的綠色冶金方法，媒質內部的介電損耗直接將微波能量選擇性地傳遞給被加熱媒質的分子或原子，宏觀上表現出加熱可選擇性、加熱均勻、熱效率高、清潔無污染等特點[1-3]。微波加熱過程是高頻電磁波與媒質相互作用的動態響應過程。電磁場分布在微波應用器腔體內部，隨著電磁波的傳播微波能，媒質熱量積累、溫度上升、載流子運動，而溫度變化和載流子運動又使得媒質的介電常數和電導率等物理參數發生改變，反過來影響電磁場分布，最終這些變化會造成加熱媒質狀態發生變化、應用器加熱效能降低，甚至造成應用器加熱失效[4-5]。

了解高頻電磁波與媒質相互作用的響應過程是優化控制加熱過程與提高應用器效能的關鍵，但由于該復雜響應過程涉及電磁場、熱傳導和載流子運動多種物理過程，必須聯立電磁場方程、熱傳導方程和載流子方程，構建多物理場方程組，從而進行計算，但是計算難度大。因此，找到分析高頻電磁波與媒質相互作用的響應過程的方法十分必要[6-7]。

微波應用器內高頻電磁波的場分布問題一般歸結為求解邊值問題。求解電磁分布邊值問題通常用全波場分析方法，主要有解析法和數值計算方法[8-9]。全波場分析方法計算的結果精確度較高，受到諸多學者的青睞，TANG等[10]基于積分方程理論研究了微小變化的微波頻率對的加熱均勻性的影響。JING 等[11]用有限差分法計算了微波加熱聚烯烴吸收劑混合物時腔體內的問題，得到了腔體內的溫度場分布。劉小明等[12]通過有限元方法分析了電磁場、材料介電常數以及導熱結構對瀝青混凝土傳熱性能的影響。但是全波場分析方法也存在以下問題：解析法對數學技巧的要求高，求解條件限制多，一般難以直接求解復雜場域和多物理場耦合問題[13]。數值計算方法建模復雜，完成一次仿真計算需要耗費大量時間，缺乏工程實用性[14]。

計算微波加熱系統電磁場分布還可以根據傳輸線理論建立微波加熱腔體的等效電路模型，通過等效電路的方法分析微波加熱腔體中電磁場的分布。等效電路模型計算簡單、計算速度快。WU等[14]研究微波加熱熱失控溫度與電場強度之間的“S 曲線”關系時，基于單模波導理論建立了微波加熱諧振腔等效電路模型。但是通過等效電路模型直接計算微波加熱問題，腔體內電磁波吸收和反射的情況被忽略，計算精度不高。亟需一種既保持等效電路模型計算速度又提高等效電路模型計算精度的計算方法。場路結合方法通過三維的全波場分析仿真，獲得相對精確的二維電路分析模型的參數，并將這些參數代入二維電路模型中用于計算，從而在保持電路分析快速性的前提下提高電路分析精確性[15]。場路結合方法在很多領域都有應用，王大朋等[16]通過場路結合的方法分析了磁軸承的懸浮力，利用磁路法推導了磁軸承懸浮力的線性化模型。毛煜茹等[17]分析微波通信系統非線性金屬結的無源互調干擾時，運用場路結合的方法精確地計算了由于金屬接觸非線性引起的無源互調及其作為二次輻射源所激發的電磁場。

綜上所述，在分析微波加熱動態響應過程時，全波場分析方法精度高，等效電路方法的計算速度快。本文提出運用場路結合的方法，分析微波應用器腔體中高頻電磁波與媒質之間相互作用的動態響應過程。首先，分析微波加熱系統各部分的阻抗特性建立等效電路模型；其次，用全波場分析的方法對應用器腔體各部分進行散射場分析，得到散射參數；然后，將分析得到的散射參數轉化為用于等效電路分析的阻抗參數，阻抗參數表征能量的轉換；最后，通過等效電路分析計算饋入腔體的微波與媒質之間的能量交換的問題，進而計算出媒質加熱溫度。

1 微波加熱系統相關基礎模型

1.1 微波傳輸等效電路模型

傳輸線理論在微波系統的分析中有著至關重要的地位，它將對電場和磁場的分析轉化為對電壓和電流的分析，從而可以將電路理論和網絡分析的方法運用到微波系統中[18]。通過傳輸線理論和傳輸線方程，可以建立電磁波在含媒質的雙端口波導中傳播時的等效電壓和等效電流關系[19]。

圖1所示為一段含任意媒質的波導的二維示意圖，設z=0 處媒質兩側區域1 和區域2 無限遠處分別有TE10模式的微波沿著波導傳向被加熱，腔內除被加熱介質和空氣外無其他媒質。

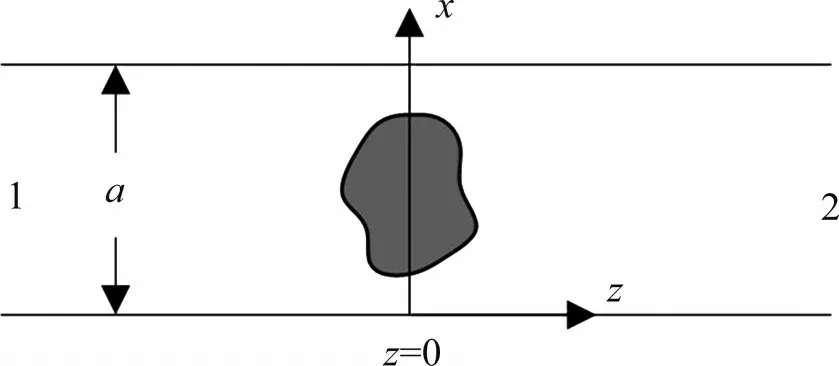
圖1 含任意媒質的波導二維示意圖Fig.1 Two-dimension diagram of waveguide with arbitrary medium

用U1和I1分別表示媒質左側從遠場到媒質的等效電壓和等效電流，U2和I2分別表示媒質右側從遠場到媒質的等效電壓和等效電流。由于媒質的存在，媒質兩側U1≠U2，I1≠I2。媒質處的電壓和電流的關系可以表示為

即U=ZI，其中：Z為阻抗矩陣，表征微波通過媒質時的損耗，是等效電路分析微波加熱時的重要參數。

1.2 微波加熱數學模型

微波加熱涉及電磁場和傳熱計算，是Helmholtz方程和Fourier熱傳導方程的雙向耦合。

變化的電場和變化的磁場相互聯系、相互激發，組成一個統一的電磁場。電磁場隨時間和空間的變化規律可以由麥克斯韋方程表示為：

式中：H為磁場強度，A/m；E為電場強度，V/m；B為磁感應強度，Wb/m2；D為電位移矢量，C/m2；Je、Jm、ρe和ρm分別為電流密度、磁流密度、電荷密度和磁荷密度；σ和σm分別為媒質的電導率和磁導率。

在微波加熱諧振腔內的電磁場分布可由式(2)推導的Helmholtz方程表示[3]：

式中：μ0和μr分別為真空磁導率和媒質的相對磁導率；ε0和εr分別為真空介電常數和媒質的相對介電常數；ω為入射微波角頻率；k0為自由空間波數；j為虛數單位。

在微波加熱過程中，媒質熱能來自吸收轉化的微波能。通過計算單位體積媒質內的微波耗散功率可以得到熱能的熱源項，微波的耗散功率可表示為

式中：Q為熱源項，表示微波耗散功率；ε″和μ″分別為介電損耗和磁滯損耗。若被加熱媒質可忽略磁滯損耗，則可令Qm=0，式(4)可表示為

計算出熱源項后，通過以下Fourier 熱傳導方程計算媒質中熱量的產生和傳遞：

式中：ρ為加熱媒質的密度；Cp為加熱媒質的比熱容；kt為加熱媒質的導熱系數；T(z，t)為加熱媒質的溫度。

初始溫度條件如下[20]：

溫度滿足表面熱平衡，邊界條件可設為[20]：

式中：h為對流換熱系數；Tair為媒質周圍環境溫度；L為媒質厚度。

以式(2)為理論基礎，通過式(1)計算得到媒質內部電磁場電場強度，代入式(5)和式(6)可得到加熱后媒質的溫度。因此，采用全波場分析結合電路的分析方法可以求解微波加熱多物理場耦合的問題。

2 場路結合方法的實現

2.1 參數轉換

在實際工程應用中，通常使用微波場散射參數S表征微波系統端口的匹配性能和傳輸損耗。S是反映端口入射波與反射波之間關系的網絡參數，在1個二端口網絡中，S矩陣包括2個反射系數(S11和S22)與2個傳輸系數(S12和S21)。其中，S11為端口1 的反射系數，表示端口1 反射波能量與入射波能量的比，S11越小，表示微波能量被反射回源端的能量越少。S21為端口1到端口2的傳輸系數，表示端口1入射波能量與端口2出射波能量的比，S21越小，表示微波在端口1到端口2傳輸過程中被吸收的能量越大。

三維全波場仿真獲得的S矩陣可以反映媒質對微波的吸收和反射，通過轉化為等效電路中阻抗參數矩陣，可以提高等效電路分析微波加熱問題的準確度。

根據微波網絡原理，波導中媒質部分可以單獨看成1個二端口網絡，網絡兩側等效電壓的關系可以表示為

即U-=SU+。其中S為散射矩陣，表示媒質的散射特性，反映了波導中媒質兩側入射波和反射波的振幅的關系[21]。

式中：Ei和Ej分別為波導i和j端口上的激勵電場；Ec為相應端口上的總電場。

在第2節中，波導中存在的媒質的阻抗特性由Z表示，反映微波通過媒質時的損耗。阻抗矩陣Z和散射矩陣S從不同的角度反映了波導中媒質對微波傳播的影響，2 種特性參數可以通過下式互相轉換[22]：

式中：ΔS=(1-S11)(1-S22)-S212。

場路結合構建微波加熱等效電路模型如圖2所示[22]。

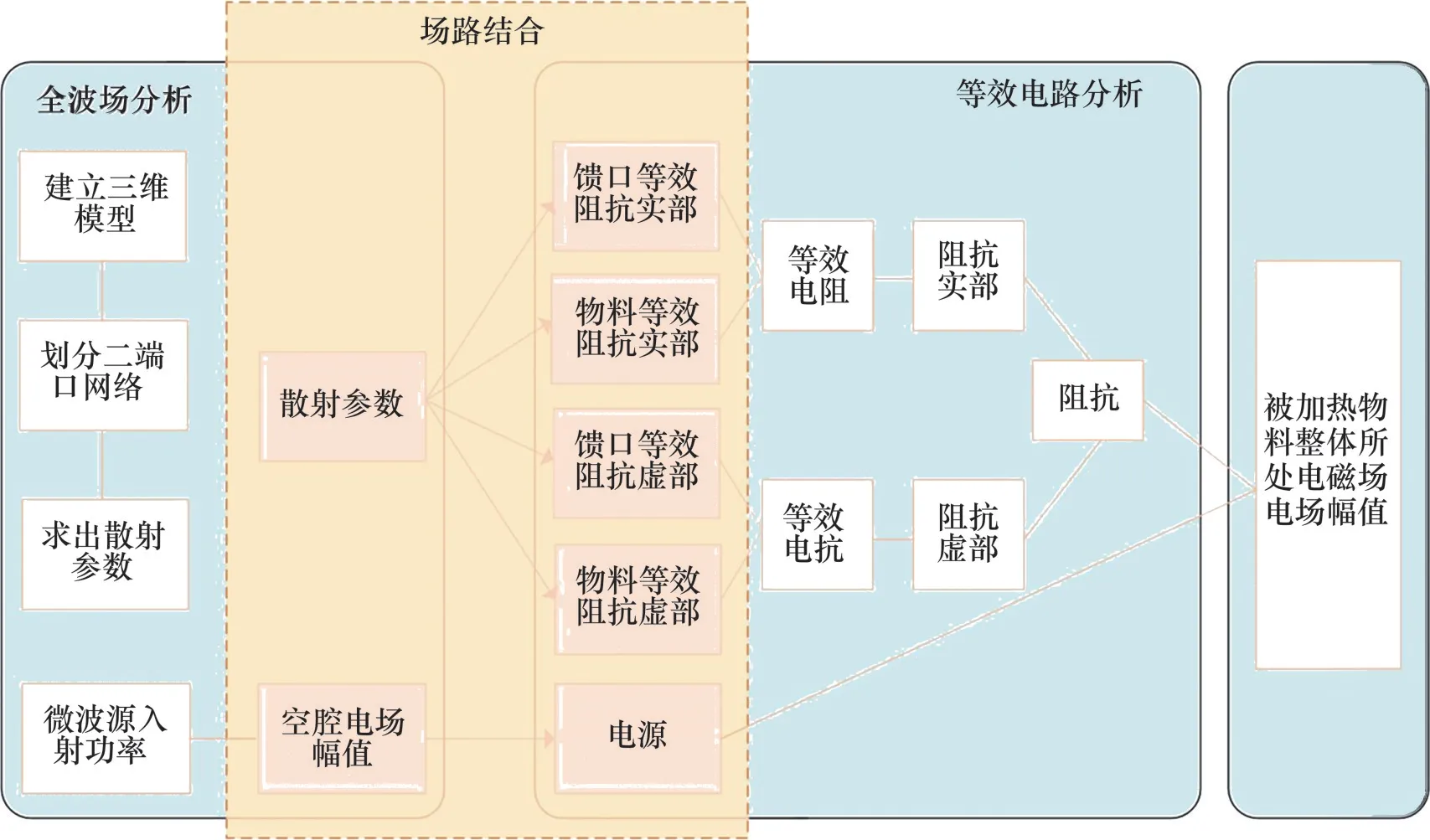
圖2 場路結合構建微波加熱等效電路模型Fig.2 Microwave heating equivalent circuit model diagram by combining field and circuit

2.2 微波加熱系統等效電路模型

微波加熱應用器系統一般是由微波發生器、傳輸波導、控制系統和微波應用器部件組成。為了便于分析微波加熱效果，忽略微波發生、傳輸、控制部分，微波加熱系統如圖3所示。

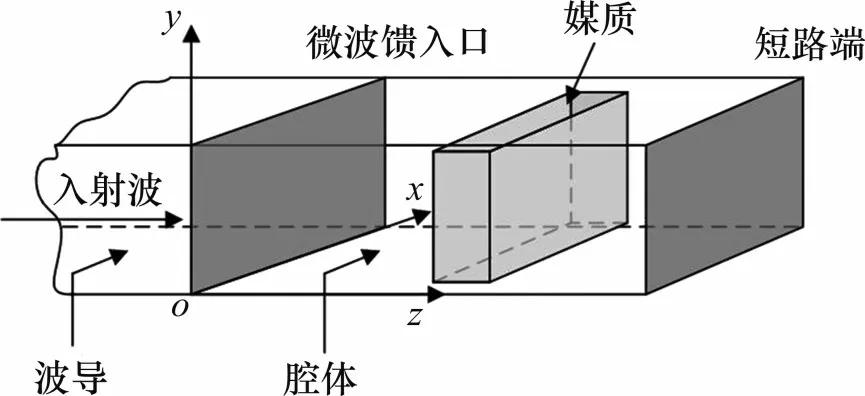
圖3 微波加熱系統示意圖Fig.3 Schematic diagram of microwave heating system

假設腔體的腔壁為理想邊界，在波傳播過程中可以把微波饋入口、媒質、短路端視為波導中的障礙物，計算障礙物的等效阻抗參數，對微波加熱系統建立等效阻抗模型，對等效阻抗進行電路變換以及等效可得到如圖4所示的電路。圖4中I為圖3 微波加熱系統中的微波源項，Ga為微波源饋入口膜片的損耗和微波源損耗，Gx+jB0為被加熱媒質的介電常數和損耗因子，Zd為微波腔體中的傳輸阻抗，表征回波損耗和傳輸損耗。

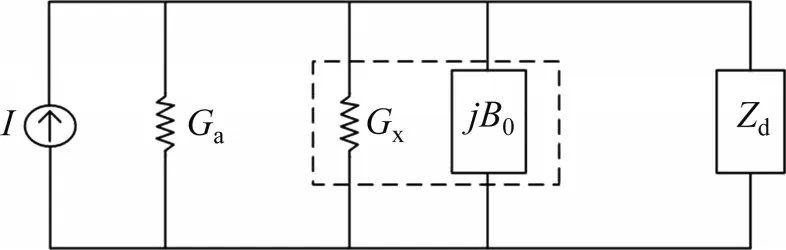
圖4 微波加熱系統等效電路Fig.4 Equivalent circuit of microwave heating system

媒質的電場與電壓呈正比例關系，可將其表示為[14]

式中：k是比例常數。

Gx+jB0可以由阻抗參數表示為[22]

Zd與微波模式、波導波數、腔體尺寸和媒質位置相關，可以表示為

式中：k10為TE10波的波導波數；L1和L2分別表示媒質兩側腔體的長度，與媒質在腔體中的位置以及腔體的長度有關。

對式(13)中的所有量，使用Ga歸一化后得到式(16)。

式中：E0為空腔電場幅值；在體積為V的空腔中E0與輸入功率P的關系可表示為[23]

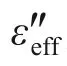
結合式(16)和式(17)，媒質部分電壓可表示為

式(18)中，變量θ直接影響場路結合算法計算的準確度。運用遺傳算法尋優，求出等效電路電源電壓與激勵電場幅值的誤差最小時變量θ的值。遺傳算法適應度函數設置為

式中：|Ei|為激勵電場幅值。

2.3 場路結合方法算法流程

基于場路結合求解微波加熱動態過程算法流程如下：

1)確定微波加熱系統模型構成，給定初始條件和邊界條件，根據腔體幾何模型和加熱媒質，劃分二端口網絡，建立微波加熱系統的等效電路模型。

2)應用式(10)～(11)，分析二端口網絡的散射場，研究二端口網絡各端口的入射波與反射波和出射波的關系，得到二端口網絡的散射參數矩陣。

3)應用式(12)將散射參數矩陣轉換為用于等效電路分析的阻抗參數矩陣；將步驟1)中設置的微波饋入功率轉換為等效電路中電源電壓。

4)通過相量法處理步驟3)所得阻抗參數與電源電壓之間的相位關系，并把等效后的電源和阻抗參數整合到等效電路模型中。

5)應用式(18)求解電路中媒質部分的電壓，并通過遺傳算法尋優，以提高所得電壓的精度。

6)應用式(13)計算媒質內的電場幅值，并將電場幅值代入式(5)，求出單位體積媒質吸收的微波功率，將吸收功率代入式(6)，求出媒質的溫度。

步驟5)中遺傳算法尋優的具體步驟如下：

首先，定義遺傳算法參數，確定種群大小、最大遺傳代數、個體長度、代溝、變異概率、交叉概率、滿足條件的適應度范圍，初始化種群。

其次，應用式(19)，計算種群中每一個個體的適應度，記錄適應度最優的個體。

再次，根據計算的適應度對種群進行隨機遍歷采樣、兩點交叉、離散變異操作，產生新的種群，遺傳代數增加。

最后，檢驗適應度是否達到適應度范圍條件或者遺傳代數是否達到最大遺傳代數，如不滿足則返回遺傳算法尋優步的第二步，如滿足則輸出最優適應度和對應個體。

3 仿真實驗及結果

3.1 微波加熱系統模型

微波加熱系統模型加熱腔體使用長×寬×高為100.0 mm×86.4 mm×43.2 mm 的長方體，波導使用WR340 標準波導。腔體內饋送頻率2.45 GHz 的TE10模式波。系統內初始溫度設置為20 ℃，微波反應腔壁和波導壁的材料為銅，腔體與波導內介質為空氣，被加熱媒質為土豆。對需要散射分析的部分用假想參考面進行劃分，模型如圖5所示[24]。建立模型中應用的初始輸入參數設置如表1所示[25]。

表1 模型初始參數設置Table 1 Initial parameter setting of model

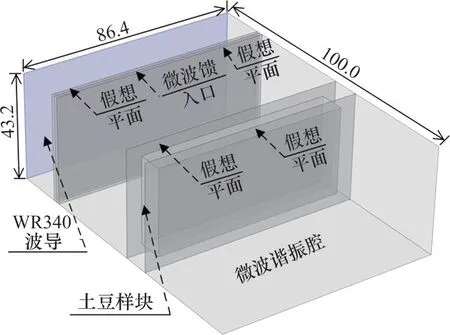
圖5 微波加熱系統模型Fig.5 Model of microwave heating system

邊界條件設定的合理性影響仿真結果的準確性。本文的仿真實驗中模型的邊界條件分為電磁邊界條件和熱傳導邊界條件。模型中，腔體壁以及波導壁的材料為銅，其電磁邊界條件控制方程為

式中：n為腔壁表面的單位法向量。

熱傳導邊界條件設置為對流熱通量，用于計算媒質與周圍環境之間的熱量交換，定義為如下方程：

式中：?T/?n為垂直于溫度域表面的溫度梯度；h為媒質周圍環境的傳熱系數；T為媒質溫度；Tair為媒質周圍環境溫度；λ為導熱系數。

3.2 散射分析模型

為得到加熱媒質部分的阻抗參數，需要對微波加熱系統模型中包含媒質的二端口網絡建立散射參數分析模型，分析模型包括一段含媒質的二端口波導，波導兩側分別設置長×寬×高為61.22 mm×86.40 mm×43.20 mm 的假想區域，其中頻率為2.45 GHz 的電磁波在真空中波長的1/2 為61.22 mm。假想區域內介質為空氣，用來模擬電磁波從無限遠處入射進二端口波導后再出射到無限遠處[24]，模型及其右視圖如圖6所示。

圖6 散射分析模型及其右視圖Fig.6 Scattering analysis model and its right view

分析二端口波導散射參數時，為保證仿真結果準確性，二端口波導2個端口外假想區域設置散射邊界條件，其控制方程為

在微波加熱系統中，為了阻止微波加熱過程中諧振腔內產生的水氣或其他氣體、雜質進入波導與磁控管接觸，需在微波饋入口位置安裝有耐高溫、抗腐蝕、良好的透波特性和低損耗特性的介質片，常用的材料有云母、高硼硅玻璃、特氟龍等[26]，分析不同材料在微波饋入口的匹配情況后，選擇匹配性能較好的材料作為微波饋入口的介質材料，3 種材料透波性能如圖7所示。從圖7可見：在電磁波頻率為2.45 GHz、介質片厚度為1 mm 的情況下，特氟龍片的透射率最高，可達99.72%，使用1 mm特氟龍片作為微波饋入口介質片微波幾乎全功率入射進加熱腔體，此時可以忽略微波饋入口反射和吸收的電磁波，即在等效電路中可忽略微波饋入口的阻抗作用。

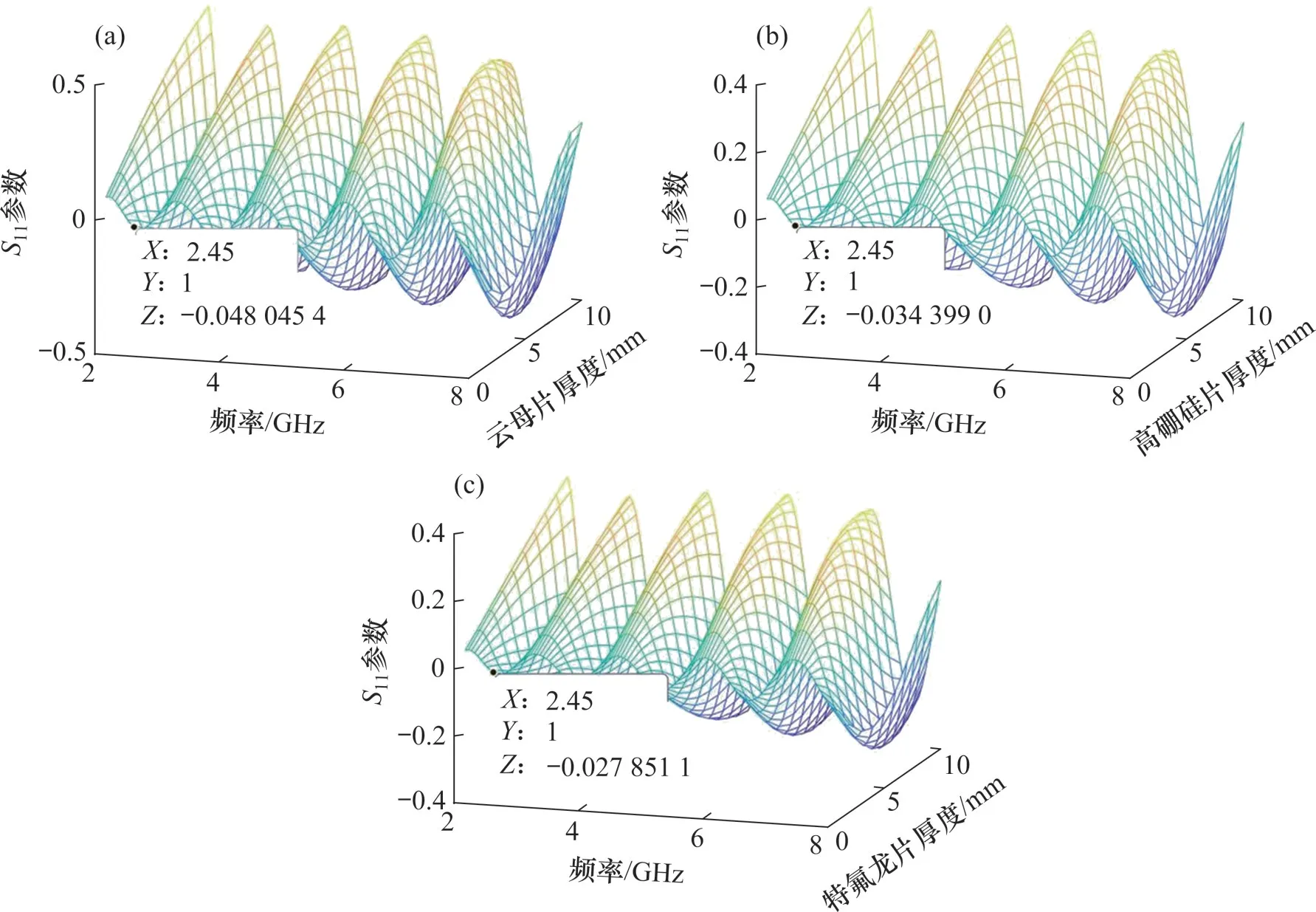
圖7 3種材料透波性能Fig.7 Wave transmission properties of three materials

圖8所示為對包含長方體媒質的二端口波導進行散射分析時，媒質周圍和媒質內部的電場強度分布。由圖8可以看出：二端口波導的散射場分析綜合考慮了媒質周圍電場和媒質內部電場的分布，反映了媒質對微波的吸收和反射作用。本文分析的不同形狀不同體積的媒質參數如表2所示。

表2 不同形狀媒質尺寸Table 2 Medium size of different shapesmm

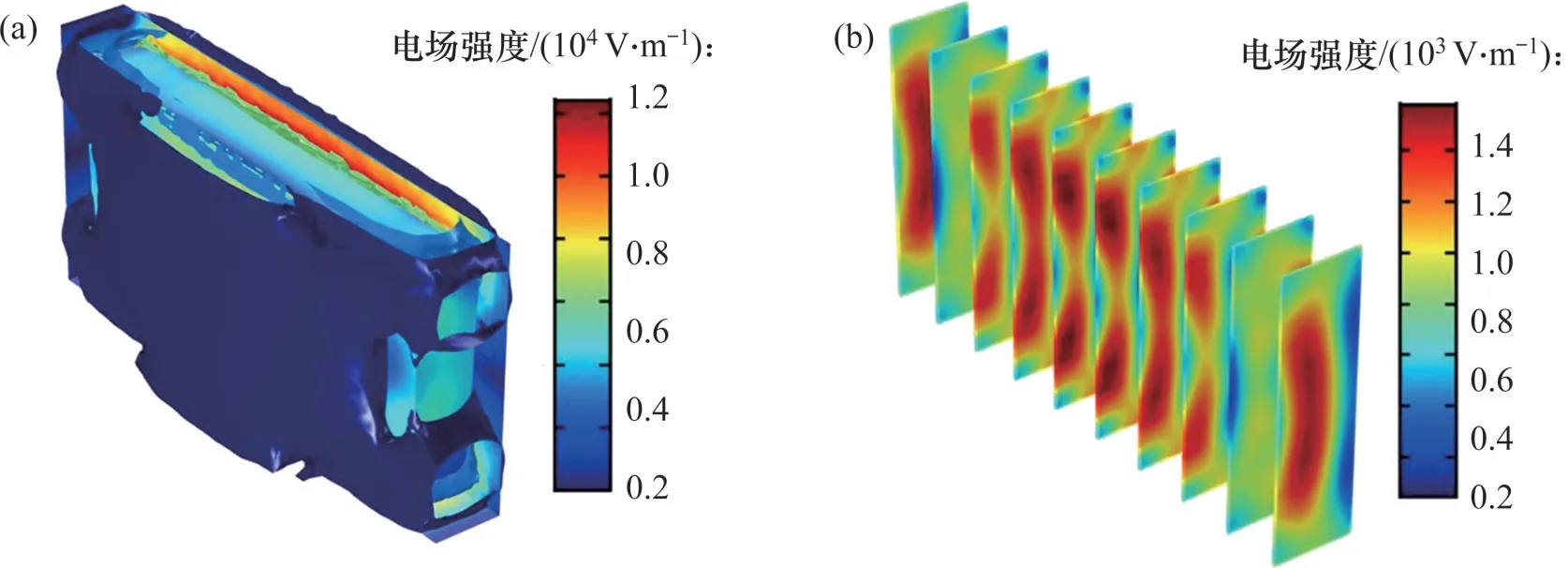
圖8 含媒質二端口波導散射場分析Fig.8 Scattering field analysis of two port waveguide with medium

對上述對不同形狀體積媒質進行散射分析，得到散射參數，并把求得的散射參數轉換為阻抗參數，所得結果如表3所示。

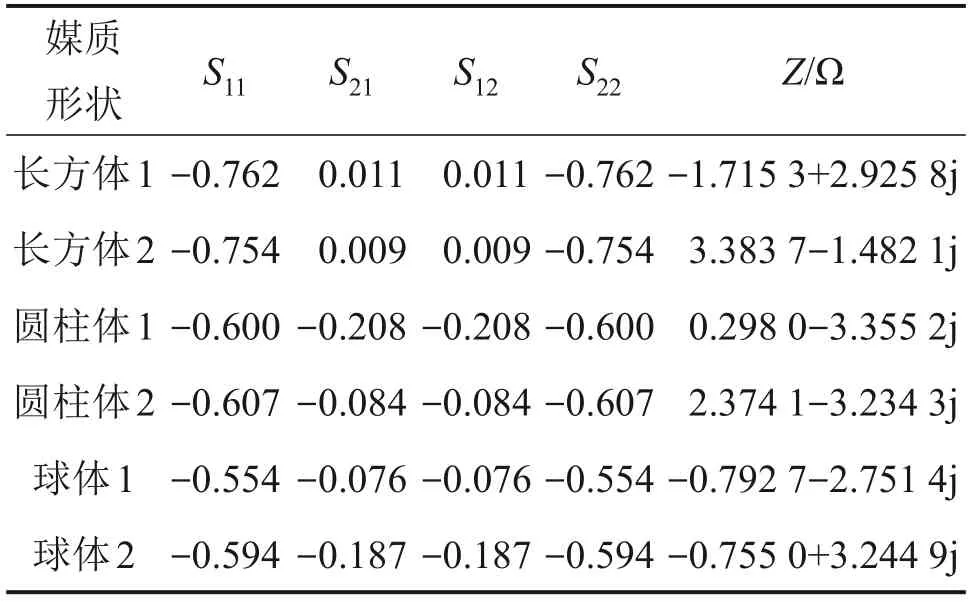
表3 不同形狀和體積的媒質S參數及等效阻抗ZTable 3 S-parameters and equivalent impedance Z of media with different shapes and volumes

以加熱媒質為長方體1為例，饋入不同功率微波時，分別通過場路結合方法和有限元方法計算加熱時媒質內平均電場強度，結果如圖9所示。由圖9可以看出：在饋入不同功率時，場路結合方法計算得到的媒質內的平均電場強度與有限元方法所得到的媒質內平均電場強度相對誤差很小。

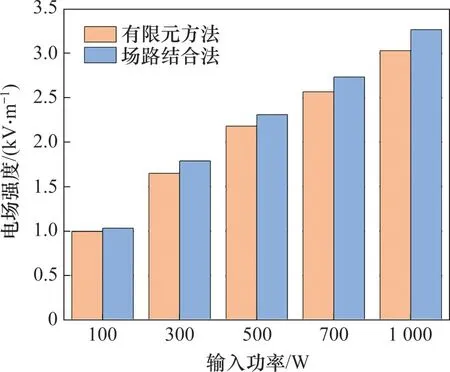
圖9 加熱時媒質內平均電場強度Fig.9 Average electric field strength in medium during heating

以加熱媒質為長方體媒質1為例，在不同輸入功率下，加熱媒質10 s，分別通過場路結合方法和有限元方法計算媒質加熱溫度所用時間，結果如圖10所示。由圖10可以看出，計算微波加熱相關問題時，場路結合方法耗時約為有限元方法的一半，體現了場路結合方法在計算速度上的優越性。

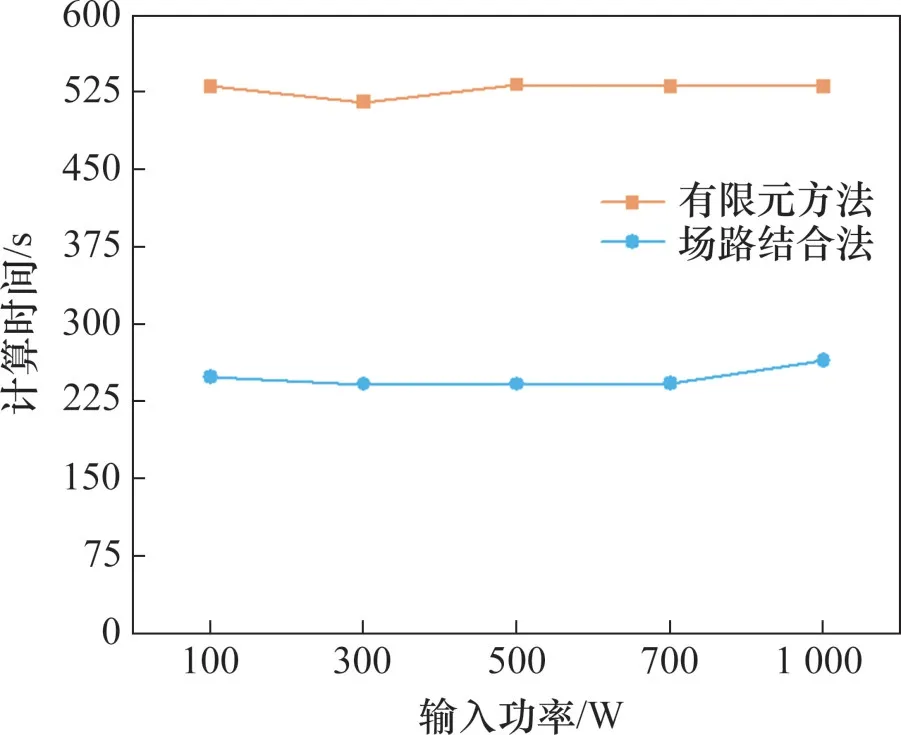
圖10 2種方法耗用時間對比Fig.10 Comparison of time consumption between two methods

結合2.2節算法流程，通過計算媒質內的電場強度，可以計算出媒質加熱的溫度。

3.3 可行性驗證

利用COMSOL Multiphysics多物理場耦合仿真實驗環境，搭建相同的微波加熱系統實驗環境，對微波加熱系統進行有限元分析。改變媒質體積、形狀、輸入功率和加熱時間等實驗變量，對比場路結合方法與傳統的有限元方法在媒質加熱效果方面的計算結果，結果如圖11所示。

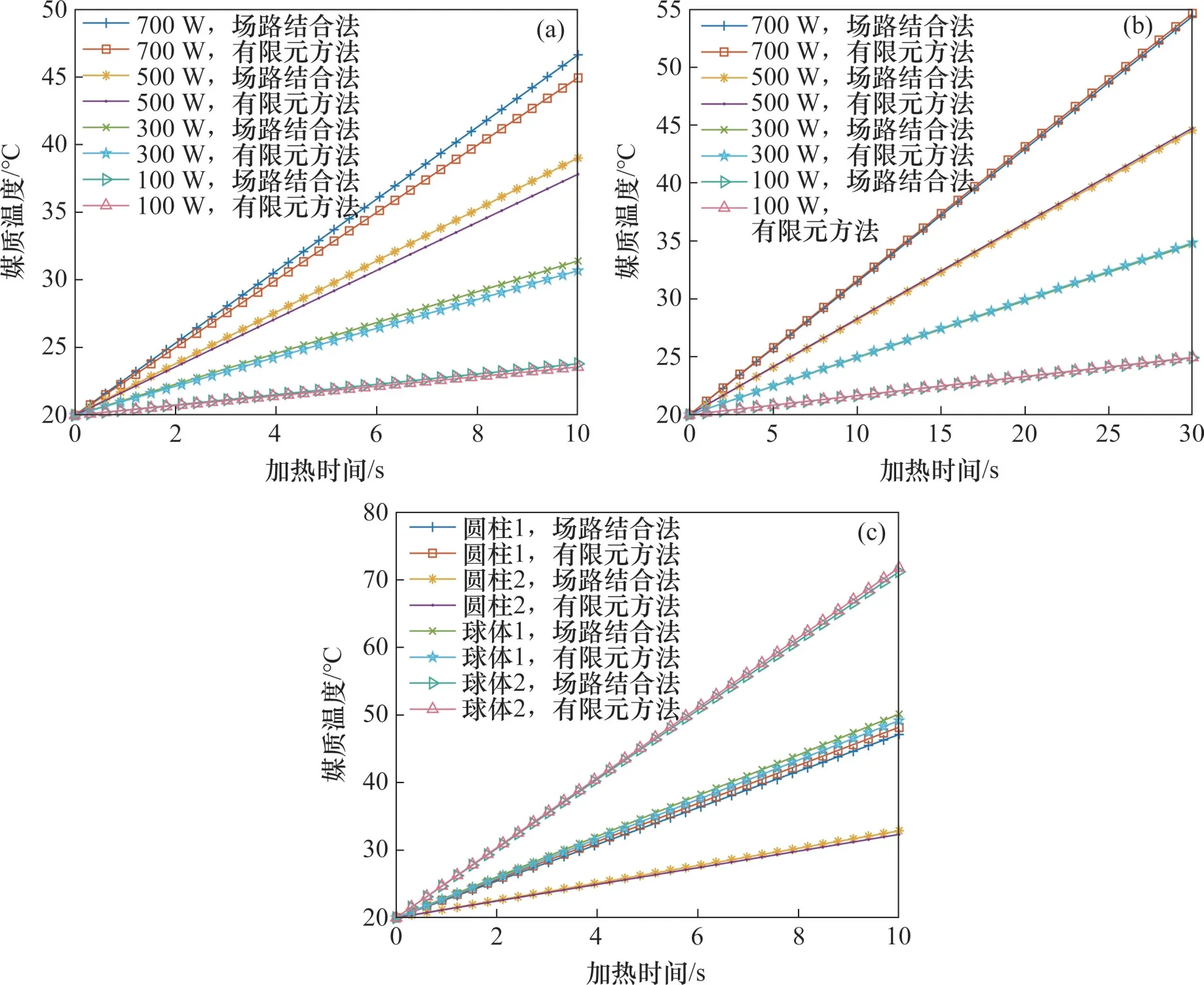
圖11 不同媒質形狀下加熱溫度計算結果對比Fig.11 Comparison of calculation results heating temperature for different shapes and volumes

1)改變輸入功率，在700、500、300和100 W這4 種輸入功率下，加熱長方體1，時間為10 s。對比2種方法得到的媒質域的平均溫度，其結果如圖11(a)所示。

2)改變長方體媒質體積和加熱時間，在700、500、300 和100 W 這4 種輸入功率下，加熱長方體2，時間為30 s。對比2 種方法得到的媒質域的平均溫度，其結果如圖11(b)所示。

3)改變媒質形狀和體積，在1 000 W輸入功率下，加熱圓柱體1、圓柱體2、球體1和球體2，時間為10 s。對比2 種方法得到的媒質域的平均溫度，其結果如圖11(c)所示。

通過3組實驗，分析不同條件下場路結合方法相對于有限元方法的計算相對誤差δ可知，場路結合方法的計算誤差在0.14%～3.77%之間，如表4所示。因此，場路結合方法能夠有效求解不同條件下的微波加熱問題。

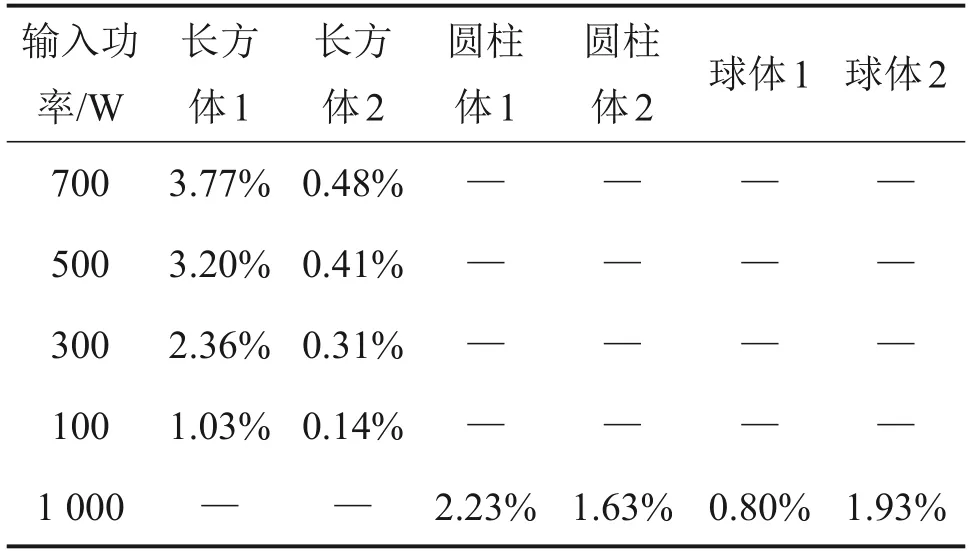
表4 場路結合方法相對于有限元方法的加熱溫度相對誤差δTable 4 Heating temperature relative error δof fieldroad combination method relative to finite element method

4 結論

1)提出一種結合全波場方法和等效電路方法的場路結合等效電路模型分析方法，求解電磁熱多物理場耦合方程組，從而求得微波加熱媒質過程中媒質的整體溫度。

2)從微波網絡理論出發，建立微波加熱系統的等效電路模型，通過全波場方法分析微波應用器腔體中電磁散射場，獲取加熱媒質、腔壁、微波饋口對微波傳輸的阻抗特性。考慮了微波反射和吸收的問題，同時采用遺傳算法提高了場路結合方法計算加熱媒質內部電場幅值的準確度。

3)與傳統有限元計算方法相比，場路結合方法求解微波加熱媒質時的計算時間大幅減少，并保持了較高的準確率。2種計算方法求得的微波加熱媒質結果的相對誤差為0.14%～3.77%，驗證了本文提出的場路結合方法的可行性和有效性。