有關教育增值分析模型的應用研究*

穆明

淄博市基礎教育研究院 山東淄博 255030

0 引言

“改進結果評價、強化過程評價、探索增值評價、健全綜合評價”是《深化新時代教育評價改革總體方案》提出的一項重要的任務，在落實這項任務時，一線教育評價工作者遇到不少挑戰，其中的難題之一就是如何實施增值評價測量。筆者在工作實踐中，通過對眾多教育增值評價案例的對比分析，在掌握統計學理論的基礎上，對教育增值分析模型進行了研究，并借助HLM 軟件對教育增值進行了精準測量。故此，本文對基于縱向數據的教育增值測量常用模型進行分析，拋磚引玉，以期為一線從事教育測量與評價的同仁深入理解應用增值評價模型提供參考。

1 教育增值的概念與測量方法

教育增值的概念是建構于學校為其學生成績增加“價值”的假設之上的，其基本思想是測量學生經過一段時間后的進步，需要在一段特定時間的開始和結束時刻測量基線和結果，測量學生學業進步的最關鍵證據是一段特定時間內的基線和最終成績數據，當然也可以需要學生個人和學校的其他背景和環境信息。由于學生的自身成長，按正常預期學生都會有進步或改進，平均成績隨之會提高，鑒于此，學校增值界定為在學生可預期的正常成長之外，由教育所帶來的額外價值，由此增值評價要考查學校的學生在一段特定時間內是否比其他學校的學生取得相對更大或更小的進步，即為超過預期的學校效能。基于對增值概念的正確理解，學校效能增值并非為學生個體增值，非起始時刻的基線成績也不必作為協變量引入增值分析模型中。

遵循統計學理論能夠分離學校經歷和學生原有特征作用于學生個體成績的統計方法，根據基于的統計技術不同帶來的分析靈敏度和復雜度的不同，對教育增值的測量主要歸納為三種主要的方法。

1.1 概要統計

概要統計用來從學生水平數據中計算學校總體水平，通過估計樣本中每所學校學生成績的原始水平，提供學校表現的簡單情況。此方法的缺點是不能估算學生的進步，因為是以學校為分析單元，在分析中會損失學生個體的詳細信息。

1.2 多元回歸分析

多元回歸分析是計算觀察分數與預期分數殘差的標準統計技術，在測量學生進步時，觀察分數是一個學生的實際成績水平，預期分數是其先前基線成績基礎上預測的水平，殘差分數用來解釋一個學生的表現是高于還是低于預期。這種方法的缺點是分析單元只能是學生水平（即計算學生殘差分數的位置）或學校水平（即計算學校殘差分數的位置）之一，前一種情況損失了特定學校中學生群體的重要信息（忽視了學校的匯聚作用），后一種情況損失了學生個體的詳細信息。

1.3 分層線性模型

分層線性模型是線性回歸的拓展和延伸，其計算殘差增值分數的原理與多元回歸相同，但是，此技術兼顧了嵌套在學校中的學生群體，允許分析單元同時包括學生和學校水平，充分考慮了上層組織的匯聚作用，在分離學校效能時，多水平模型是一種比概要統計和標準多元回歸更成熟的方法，應用此方法可以無偏估算學生群體的學校殘差，更重要的是檢驗單個學校結果的統計顯著性。

在學業評價增值分析中常用到組織模型和發展模型，兩種模型均能體現上層單位如學校的匯聚作用，以此進行上層單位的增值效能分離。針對單一學生年齡群體在收集、記錄基線和結果評估的數據時，需要保證個體學生的記錄能在以后都能準確匹配，以此為樣本建立的模型為組織模型；針對考查跨時間的趨勢或在增值表現中的改進，需要收集至少三個連續時間點學生群體的相同結果和基線數據，以此為樣本建立的模型為發展模型。在計算學校表現的增值測量時，一般不需考慮教育和學校的過程信息，因此，在進行教育增值測量時，不必引入教育和學校發展過程中的變量因素來實現擬合學校增值的主效應。

2 分層線性模型理論

分層線性模型的建模基本思想為：一是將分層結構數據在因變量上的變異分為組內變異與組間變異兩個層次（隨機誤差方差與參數方差）；二是分別在不同層次上引入自變量對二者進行解釋（也可只在其中一層引入協變量）。

如以區域內學校學生的學業成績建立的二層線性模型為例：組內（層1）模型對同一所學校學生的學習成績進行線性回歸，取得不同學校線性回歸方程的模型參數（截距與斜率）估計值；組間（層2）模型分別以層1 模型的線性回歸模型參數（截距與斜率）作為因變量進行回歸。

分層線性模型可理解為對組內（層1）模型的回歸截距與斜率系數的再回歸，根據模型方程的表達形式（矩陣或標量）通常應用迭代廣義最小二乘法或迭代加權最小二乘法進行模型參數優化，采用HLM 分層線性模型統計軟件進行參數估算及顯著性檢驗[1]。

分層線性模型不是一個單一模型，其包括了從最簡單到最復雜的多個子模型。與教育增值分析研究相關的基礎模型有：零模型、隨機截距模型（協方差分析模型）、隨機系數回歸模型。其中隨機截距模型可視為隨機系數回歸模型的特例。零模型和隨機系數回歸模型的建模原理闡釋如下。

2.1 零模型

零模型也稱為空模型，是最簡化的分層線性模型，雖然不能直接用來進行分層數據分析，但它是構建分層線性模型分析的起始點。零模型的層1（組內）模型與層2（組間）模型都不包含解釋變量。其數學模型為：

層1 模型：yij=β0j+εij

層2 模型：β0j=γ00+μ0j

其中，γ00是樣本總體中因變量的平均值，μ0j是與第j個層2 單位相關聯的隨機效應。

將層2 模型代入層1 模型可得組合模型：

yij=γ00+μ0j+εij

在零模型中結果變量的方差由組間方差與組內方差兩個部分組成，根據零模型估算的隨機系數方差和隨機誤差方差，可進行組內相關系數的計算：

ρ=τ00/(τ00+σ2)

其中，σ2為組內隨機方差，τ00為組間參數方差。

ρ值表示層2 單位之間的差異在層1 結果變量的總方差中所占的比例。如果ρ值很小（通常小于0.059），說明層2 單位之間的差異不大，不需要采用分層線性模型，采用常規的一元或多元線性回歸方程進行統計建模就可以進行統計分析，如硬性采用分層線性模型可導致統計數據的不精確；反之，則需要采用分層線性模型。通常在應用帶有協變量的分層線性模型進行統計分析之前，一般都需要建立零模型來進行判斷是否需要采用分層線性模型。

2.2 隨機系數回歸模型

隨機系數回歸模型是完整分層線性模型的最簡形式，它在零模型的基礎上，將層1 模型的截距和斜率系數設定為在層2 單位之間是隨機變化的，但層2 模型不引入協變量對層1 模型的截距與斜率系數中存在的變異進行解釋。與隨機系數模型密切相關的一項統計技術是協變量的測量定位，一般采用對中方式,對中在分層線性模型中具有非常重要的作用。在經典的協方差模型中通常選擇基于總均值對中,即采用標準測量方法。其數學模型為：

層1 模型：yij=β0j+β1j(xij-)+εij

層2 模型：

β0j=γ00+μ0j

β1j=γ10+μ1j

其中，γ00是層2 模型所有層2 單位的回歸截距的均值，γ10是層2 模型所有層2 單位的回歸斜率的均值。μ0j、μ1j分別是層2 模型在回歸截距和回歸斜率上與第j個層2 單位有關的特性增量。

將層2 模型代入層1 模型，可得組合模型：

τ00表示層1 所有截距假定服從先驗正態分布的無條件方差，τ11表示層1 所有斜率假定服從先驗正態分布的無條件方差，τ01表示層1 所有截距與斜率的無條件協方差。在對回歸截距均值γ00和回歸斜率均值γ10的估計值進行統計檢驗（t檢驗）為顯著時，說明研究總體中的固定效應不為0；同樣對隨機效應參數μ0j與μ1j進行統計檢驗（卡方檢驗），如果無法拒絕二者都等于0 的原假設，就意味著研究總體中的各單位的層1 系數大致相等，即為固定值不存在隨機變化，可取消層2 單位中的隨機項μ0j與μ1j。

隨機系數回歸模型的誤差項包括三部分：

εij為層1 誤差；

μ0j為層2 截距模型的誤差；

μ1j(xij-)為層2 斜率模型的誤差μ1j與層1 協變量的乘積。

層2 單位的平均效能（用μj表示）為組合模型的總殘差減去層1 的平均隨機誤差的剩余部分，因層1 隨機誤差的不可測性，根據經典測量真分數理論的數學模型，故定義層2 效能方差（層1 真值方差）與總殘差方差（樣本均值總方差）的比率為可靠性系數（λj）即信度，用可靠性系數（信度）與總殘差的乘積作為層2 單位的效能，從而分離提取層2 單位的增值量。

3 模型案例分析

分層線性模型的一項重要的應用就是檢測單個組織效應，其常見的應用大致分為在組織研究中的應用和個體變化研究中的應用，有關組織如何影響個人的問題可采用組織模型實現，有關多個時點上個體變化現象的問題可采用發展模型實現。

3.1 組織模型

對學校增值的測量是以該校學生的背景和基線能力而預測的平均成績為回歸數據值，如果實測學校平均成績分值高于此預測值，這樣的學校被認為是好學校。每個學校的效能增值指標可以從其實測平均成績與其預測的平均成績的差中分離提取。考慮到殘差效應估計值的穩定性，出于追求統計有效和計算穩定性的目的，通常采用經驗貝葉斯估計方法，能夠提供判定測量學校增值的穩定指標，借鑒國內外增值評價成功案例的增值效能算法，優選采用隨機截距模型進行學校增值分析。另外，在計算學校表現的增值量時，一般不用教育和過程信息，常用的學校業績增值分析模型為隨機截距模型，它是完全模型的一個特例。其數學模型為：

層1 模型：yij=β0j+β1j(xij-)+εij

層2 模型：β0j=γ00+μ0j

將層2 模型代入層1 模型，可得組合模型：

yij=γ00+β1j(xij-x)+μ0j+εij

類似“水漲船高”的原理，因學校j的所有學生都在該學校上學，所以都有一個增值效應μ0j疊加到他們的預期回歸分值上，j個學校在單因素隨機效應協方差分析中構成為獨立的組，模型的實現目的是提取每個層2 單位效應的估計值。每個學校的OLS（最小二乘法）估計效應為：μ_j是協方差分析中的校平均殘差，對于樣本少的學校產生的μ_j估計值不穩定。為此，采用分層線性模型的經驗貝葉斯殘差作為學校效應估計值（用μj表示），用前文提到的可靠性系數（λj）作為提取因子，計算公式為：

μj=λjμ-j

其中：

λj=τ00/[τ00+σ2/nj]

根據貝葉斯推斷理論，在給定學校的平均成績后每個學校的隨機效能μ0j的后驗分布都服從均值為μj，方差為Vj的正態分布[2]。

其中：

Vj=1/[1/τ00+nj/σ2]

據此可以估計μ0j的95%置信區間（可能值域）：

μj±1.96Vj1/2

通常只有置信區間的最大值在0 值以下的，表明學校效能低于平均水平，通常只有置信區間的最小值在0 值以上的，表明學校效能高于平均水平，置信區間包含0 值的表明學校效能并無統計學意義上的差異。因此，可以借助置信區間來實現增值結果的呈現，根據置信區間的端點值進行學校效能分類，達到學校對數據的所有權和保證結果的保密性要求。

作為組織模型應用研究實證案例，以淄博市2022年高三數學模考（入口成績）和一模（出口成績）成績進行分析建模，將兩次成績進行線性等值處理后，以學生為層1、學校為層2 建立兩層線性模型，先建立空模型進行可行性分析。空模型檢驗結果如表1所示。

表1 空模型檢驗結果

由零模型估算的跨級相關系數（ICC）達到47.59%，說明47.59%以上的總變異是由層2 學校之間的差異引起，也即學校的差異是影響成績的主要原因，因此，必須建立分層線性模型進行統計分析，所建立的隨機截距模型檢驗結果如表2所示。

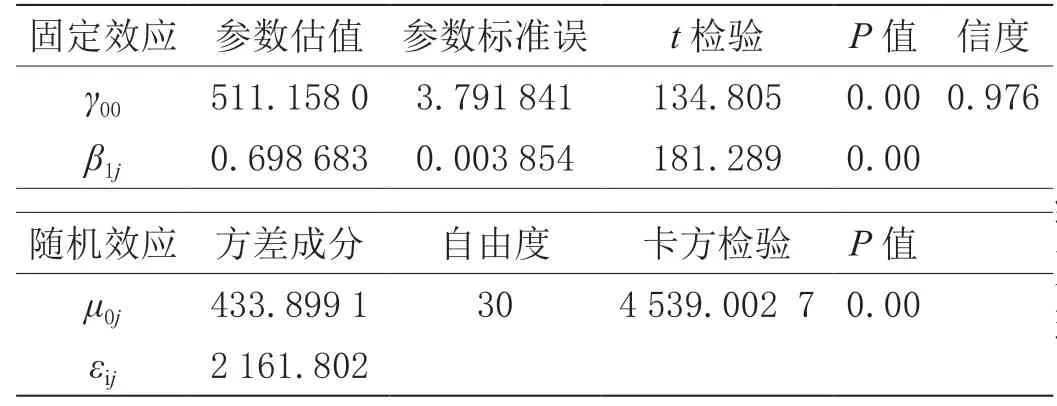
表2 隨機截距模型檢驗結果

3.2 發展模型

為了考查跨時間的趨勢（效能）或在增值表現中的改進，需要建立把多次觀察結果作為時間的某種數學函數的模型，即發展模型。本模型的輸入為學校的平均成績，過程是時間變量，結果輸出學校的平均成績增值效應。通過對連續幾個年度（至少3 個年度）的學校平均成績建模，實現測量每個學校在年度變化中的進步程度。基于所采集到的數據，建立包含時間和學校變量的分層線性模型。作為發展模型應用研究實證案例，以淄博市連續3年中考平均總分建立隨機系數回歸為例，兩層數據分別是第一層的時間水平和第二層的學校水平。模型為：

層1 模型：Yti=π0i+π1i*yearti+εti

層2 模型：π0i=β00+γ0i

π1i=β10+γ1i

組合模型：

Yti=β00+β10*yearti+γ0i+γ1i*yearti+εti

其中，Yti代表學校i的第t 時刻考試平均分，對時間變量2019年、2020年、2021年的編碼可以為0,1,2。εti為學校i的第t 時刻與線性回歸的離差（隨機誤差）。

t 時刻殘差、方差為：

eti=γ0i+γ1i*yearti+εti

Var(eti)=τ00+2yearti*τ01+yearti2*τ11+σ2

由學校引起的差異效能計算：鑒于要比較學校不同年度之間的增值這一目的要求，基于發展變量的線性模型，學校的某年度總殘差由學校給定年度線性回歸當年度（層1）的隨機誤差εti與學校（層2）之間因教育發展引起的差異γ0i+γti*yearti兩部分組成。由學校發展引起的殘差即學校效能可靠性系數（信度）為：

λ t i=τ00+ 2 y e a rti τ01+ y e a rti2*τ11/τ00+2yearti*τ01+yearti2*τ11+σ2

i學校某年度的凈效能提取公式為：μti=λtieti

i學校t 時刻相對零時刻的效能增值=μti-μ0i

作為發展模型應用研究實證案例，以淄博市連續3年（2019—2021年）中考平均成績進行分析建模，將3 個年度的中考平均成績進行線性等值處理，如表3所示。

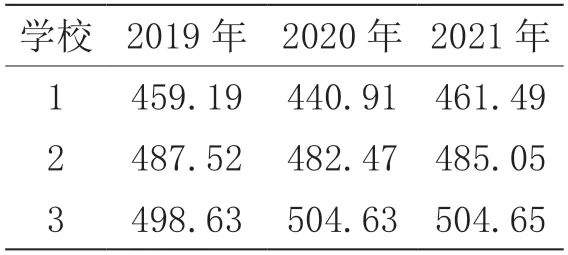
表3 淄博市中考成績等值分

先建立空模型進行可行性分析。空模型檢驗結果如表4所示。

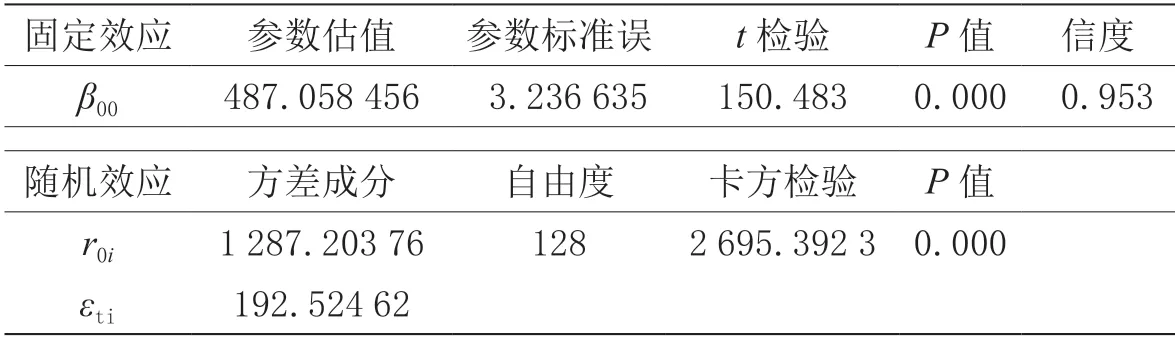
表4 空模型檢驗結果

由零模型估算的跨級相關系數（ICC）達到86.99%，說明86.99%以上的總變異是由層2 學校之間的差異引起，也即學校的差異是影響中考成績的主要原因。因此，必須建立分層線性模型進行統計分析，所建立的隨機系數回歸模型檢驗結果如表5所示。

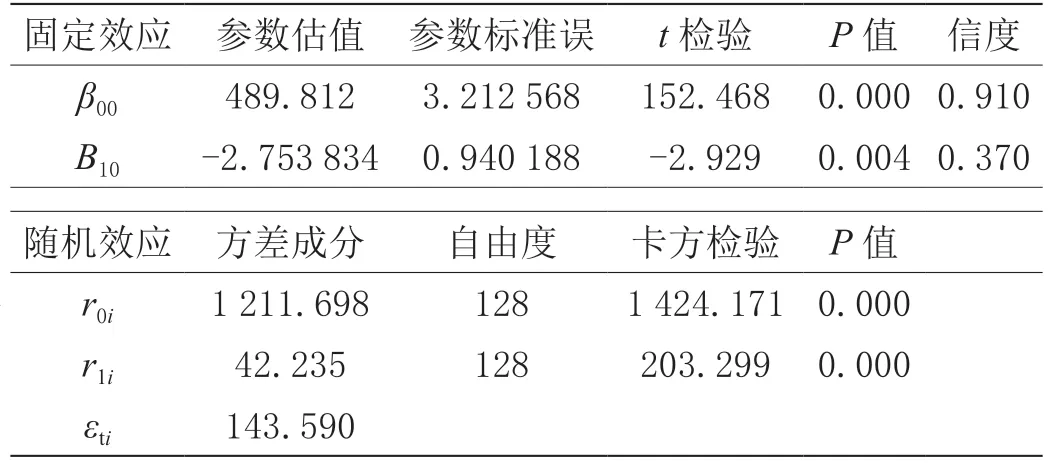
表5 隨機系數回歸模型檢驗結果

從固定效應看出，初始時刻（2019年）的學校平均分（截距）回歸值為489.812，斜率系數為-2.753 834，檢驗結果達到顯著性水平（P＜0.05），層1 的誤差變異為143.590，說明學校在每年中考成績之間的變異程度較大。

從隨機效應看出，截距和斜率在不同學校之間的變異非常顯著（χ2值分別為1 424.171 和203.299），說明學校之間在初始年度平均分和不同考試年度間變異比較明顯，并且從方差成分的大小可以看出，變異主要發生在截距上，即學校在初始年度平均分的變異遠大于不同考次之間的變異。從層1 系數的信度估計結果來看，截距項估計的信度比較高（0.910）。一般來講，如層1 方程某系數的信度較小，在進一步的分析中可以把它設為沒有隨機成分的固定參數。最后進行歷年中考學校增值比較分析：隨機抽取某區縣的3 所學校作為分析樣本對2019—2021年學校中考平均成績的增值情況進行評估，增值評估數據結構如表6所示。

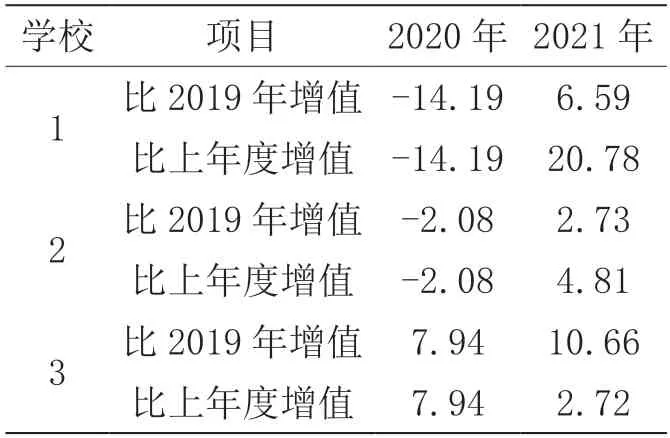
表6 區縣學校的增值評估數據表

4 結束語

總之，分層線性模型是當前教育測量處理增值評價問題的最新技術，隨著教育評價和教育督導關于學校增值評價政策措施的進一步出臺及落地實施，學校增值指標必將作為學校評價與自我評價的有效工具，參照本文提供的增值分析測量模型，可以為教育增值評價的有效實施提供可借鑒的思路。