節理幾何特征對爆破裂紋擴展的數值模擬研究

費鴻祿,山 杰,包士杰,蔣安俊

(遼寧工程技術大學爆破技術研究院,遼寧 阜新 123000)

鉆爆法破碎巖體過程中,炸藥爆炸后,爆炸沖擊波作用于炮孔近區巖體,隨著沖擊波擴散距離的增加,沖擊波逐漸減弱為應力波,應力波對巖體的破壞和裂紋的擴展起著非常重要的作用。在天然巖體中存在著大量的裂隙、層理、節理等結構面,結構面的存在導致巖體有明顯的不均勻性和各項異性,當爆炸應力波遇到節理面時,不同節理幾何特征產生的反射、透射、繞射應力波的區域與大小不一樣,從而改變爆炸應力波對巖體的作用效果、破壞模式以及爆破裂紋擴展范圍,最終改變巖體爆破效果。國內外學者對節理巖體爆破以及裂紋擴展規律進行了一些研究,劉婷婷等[1]通過數值模擬方法研究含充填節理巖體中應力波的傳播規律,發現充填厚度的遞增會降低透射系數,節理數量對透射系數的影響與節理間距有關;潘長春等[2]基于模型試驗研究了含裂隙巖體爆破時,爆破振動波的傳播規律,結果表明裂隙的存在顯著降低了爆破振動效應;丁晨曦等[3]基于模型試驗研究了張開節理對切縫藥包爆生裂紋擴展的影響,指出定向裂紋擴展不會穿過張開節理,而是在節理端部產生翼裂紋;魏晨慧等[4]指出初始應力場的作用不利于裂紋的擴展,節理對裂紋沿節理面方向的擴展具有導向和促進作用;楊仁樹等[5]通過模型試驗,研究不同炮孔與節理間距下節理處起裂形式,指出節理處起裂有爆生裂紋擴展至節理之前或之后節理處起裂2種形式;趙安平等[6]探討了節理強度、剛度、間距、傾角對爆破效果的影響,認為在節理巖體中爆破時,爆區內的節理發育程度與爆破效果呈負相關;Wang Y等[7]基于數字激光動態焦散線實驗系統,進行了爆炸載荷下垂直開縫PMMA介質中的裂紋擴展實驗,指出翼裂紋擴展初始階段,剪切波起主導作用,膨脹波起次要作用,節理傾角為45°時,翼裂紋擴展長度最長;Yang X等[8]基于爆炸加載實驗和AUTODYN軟件模擬實驗試件的動態裂紋擴展過程,指出充填物類型、角度和距離與反射和吸收的應力波能量存在相互制約的關系。

從上述研究現狀來看,國內外學者在巖體中節理的不同幾何特征對爆破裂紋擴展影響的研究較少,因此,基于前人的研究,首先探討和選擇爆破破壞理論及數值驗證的RHT本構模型,其次利用有限元仿真軟件,建立3組不同節理幾何特征的巖體準二維模型,對巖體耦合爆破裂紋擴展進行數值模擬。最后研究分析了不同節理寬度、節理長度、節理彎度(彎曲程度)對爆破作用下裂紋擴展的影響規律。

1 巖體爆破破壞理論及數值驗證

1.1 巖體爆破破壞理論

根據應力波與爆生氣體綜合作用破壞理論,結合藥包的內部作用可知:炸藥在巖體中爆炸后,炮孔周圍巖體沿著炸藥中心產生不同程度的徑向損傷,按照損傷程度依次為粉碎區、裂隙區和振動區。巖石爆破裂紋擴展,其耦合裝藥粉碎區半徑計算公式[9]如下:

(1)

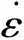
裂隙區半徑公式[9]為

(2)

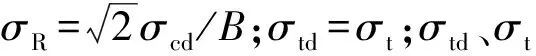
1.2 數值驗證

1.2.1 材料模型

1)巖石材料模型。RHT本構模型[10]是由Riedel等提出的一種針對混凝土和巖石等脆性材料的高級損傷模型。它引入彈性極限面、失效面和殘余強度面,分別描述材料的初始屈服強度、失效強度及殘余強度的變化[11];它包括強度模型和損傷模型,通常與p-a狀態方程共同使用,p-a狀態方程用來描述多孔隙的脆性材料壓力的壓縮過程;強度模型主要分為彈性、線性強化、損傷軟化3個階段,3個階段的表達式[12]如下:

(3)

(4)

σr=Af·(P*)nf

(5)

RHT本構的累積損傷表達式[12]為

(6)

(7)

因此,RHT模型可以模擬巖石在動態載荷下的拉伸和壓縮損傷演化[13],用于模擬爆破裂紋擴展優勢明顯[14]。巖體模型材料的參數通過理論計算和參數研究確定[14-15],其部分主要參數如表1所示。

表1 巖體模型參數

2)炸藥本構模型及狀態方程。炸藥選用*MAT_HIGH_EXPLOSIVE_BURN和JWL狀態方程來描述,其JWL狀態方程表達式為[16]

(8)

式中:P為爆壓;V0為初始相對體積;E0為初始內能;A、B為材料常數;R1、R2、ω為狀態方程常數。其具體參數如表2所示。

表2 炸藥材料及狀態方程參數

3)耦合空間(空氣)材料模型及狀態方程。耦合空間(空氣)采用*MAT_NULL材料模型,其狀態方程為*EOS_LINEAR_POLYNOMIAL,具體參數如表3所示。

表3 耦合空間(空氣)材料及狀態方程參數

1.2.2 數值模型

為驗證選取的參數、材料模型以及巖體爆破裂紋擴展數值模擬的準確性,利用有限元分析軟件,按照所選的材料本構模型及參數,建立數值模型(見圖1),對單孔耦合裝藥爆破裂紋擴展進行模擬。為了簡化數值模擬計算、減少模擬結果所占計算機的存儲空間,建立一個二分之一、z方向為一個單元格的準二維模型,其中AB長400 cm,AC長200 cm,炮孔直徑5 cm,因其研究耦合裝藥下爆生裂紋擴展規律,則裝藥直徑為5 cm,CD定義為對稱邊界條件,AB、BD、AC定義為無反射邊界條件,約束巖體z軸方向不動。黃佑鵬等[17]指出當耦合空間半徑大于炸藥半徑10倍時,計算結果是正確、收斂的,因此取空氣長75 cm、寬為37.5 cm,設置模型網格尺寸大小約為0.5 cm×0.5 cm×0.5 cm,炸藥網格單元54個,耦合空間(空氣)網格單元11 204個,巖體網格單元319 957個,其網格劃分如圖2所示。為了避免網格畸變過大,導致產生負體積運算錯誤,因此有限元模擬采用流固耦合算法,炸藥與耦合空間采用ALE算法,巖體采用Lagrange算法。

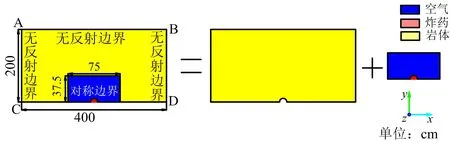
圖1 數值計算準二維模型Fig.1 Numerical calculation of quasi-2D model

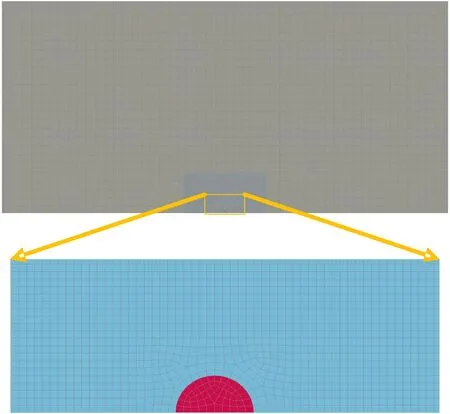
圖2 模型網格劃分Fig.2 Meshing of model

1.2.3 數值實驗驗證

在爆破過程中,RHT模型損傷(Damage)云圖可以反映巖體損傷情況,巖石未損傷時,Damage=0,巖石完全損傷時,Damage=1[18]。炸藥在巖體中爆炸時,炸藥爆炸的強烈沖擊波與爆生氣體作用于炮孔近區巖體,形成爆破空腔,產生粉碎區;隨著爆炸沖擊波在巖體內繼續傳播逐漸減弱為應力波,炮孔附近的巖體在爆炸應力波作用下開始產生徑向、環向裂紋,遠區裂紋呈放射狀分布,形成裂隙區,單孔耦合爆破理論結果和數值模擬結果分別如圖3和圖4所示。

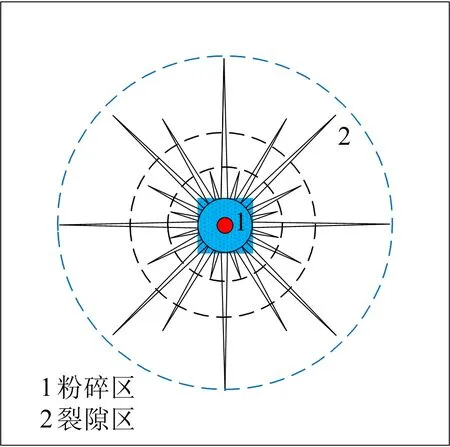
圖3 單孔耦合爆破理論結果Fig.3 Theoretical results of single-hole coupled blasting

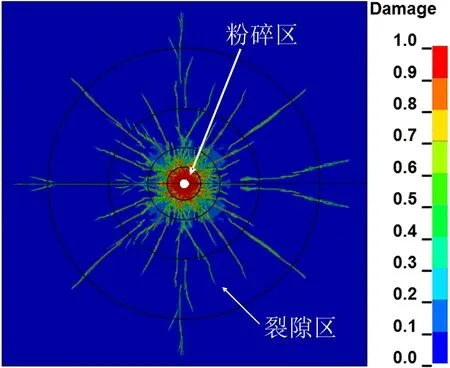
圖4 單孔耦合爆破數值結果Fig.4 Numerical results of single-hole coupled blasting

可以看出,理論結果與基于RHT模型的數值模擬結果裂紋擴展模式及損傷分布的一致。通過Ls-propost后處理軟件中的measure板塊得到粉碎區與裂隙區的半徑分別為12.7、167.2 cm。通過式(1)、式(2)及表1、表2理論計算粉碎區與裂隙區半徑分別為14.2、165.8 cm,數值模擬獲得的粉碎區與裂隙區的半徑與理論計算結果基本一致。因此,所采用的RHT模型及相關材料參數適用于研究爆破裂紋擴展模式及巖體的損傷情況,且進一步用于研究節理幾何特征對爆破裂紋擴展的影響。

2 數值模擬方案

運用ANSYS/LS-DYNA軟件,建立3組不同節理幾何特征的數值模型。第1組是不同節理寬度條件下的巖體爆破,節理長度為40 cm,節理距炸藥中心60 cm,節理寬度分別為1、2、3、4 cm,對應的模型編號分別為I、II、III、IV,用于考察節理寬度對巖體爆破裂紋擴展的影響。第2組模型是在相同節理寬度(1 cm)及位置(距炸藥中心水平位置60 cm)條件下建立節理長度分別為60、80、100 cm的模型,模型編號分別為V、VI、VII。第3組模型是在相同節理寬度(1 cm)及距炸藥中心水平位置60 cm條件下,分析節理彎曲程度對爆破裂紋擴展的影響。為了定量確定節理彎度,引用彎度定義,彎度是中弧線離弦線的最大距離與弦長度的比值。采用半徑、角度、彎度共同確定節理的形狀和位置,半徑為圓心到節理的距離,角度為節理端部和圓心的連線與水平方向的夾角。以模型I中的垂直節理(彎度為0)、長度及其距炮孔中心的距離作為參考,建立3種不同彎曲程度的節理:經計算,半徑與角度分別為40 cm、57.30°的節理對應的節理彎度為0.128;半徑與角度分別為60 cm、38.20°的節理對應的節理彎度為0.084;半徑與角度分別為80 cm、28.65°的節理對應的節理彎度為0.063,其模型編號分別為VIII、IX、X,具體彎度、半徑及角度如圖5所示。以上數值模擬不同幾何特征的節理均采用*MAT_PLASTIC_KINEMATIC材料本構模型,其力學參數[19]如表4所示。

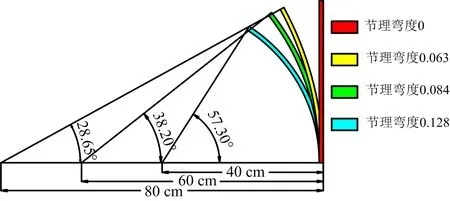
圖5 不同節理彎度Fig.5 Camber of different joints

表4 節理材料模型參數

3 爆破裂紋擴展數值模擬結果分析

3.1 節理寬度對爆破裂紋擴展的影響

在不同節理寬度對爆破裂紋擴展的影響數值模擬中,選擇基于已驗證的巖體、炸藥本構模型及參數,對含節理寬度1、2、3、4 cm的巖體進行爆破模擬,設置與數值驗證相同的邊界條件、網格尺寸及求解時間等選項,其數值模擬爆破裂紋擴展結果如圖6所示。

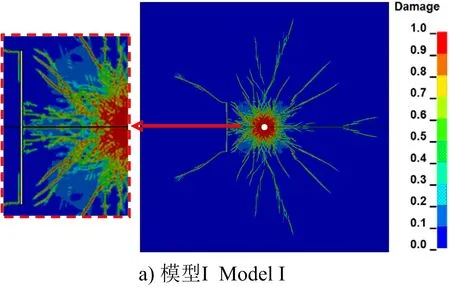
圖6 不同節理寬度條件下的爆破裂紋擴展Fig.6 Explosion crack propagation under different joint width conditions

從圖6可以看出,對于不同節理寬度的4種模型,粉碎區的半徑范圍、爆破裂紋擴展形式大致相同,說明節理寬度大小對粉碎區裂紋擴展影響較小;節理端部產生翼裂紋,且翼裂紋先呈水平擴展,后翼裂紋改變擴展路徑,這是由于爆炸應力波擴散至節理面時,應力波發生反射、透射與繞射導致節理端部發生應力集中現象,應力強度因子超過巖體斷裂韌度使巖體開裂并擴展,形成水平和弧形翼裂紋,且水平翼裂紋長度隨著節理寬度的增加遞增。

觀察圖6中炮孔與節理之間巖體裂紋發展情況可以發現,隨著節理寬度的增加,朝向節理擴展的裂紋范圍逐漸增大,裂紋逐漸變粗變長,此部位巖體損傷越嚴重。

為分析其原因,在節理中間距炸藥中心水平距離30 cm位置處選擇參考點E(見圖7)。

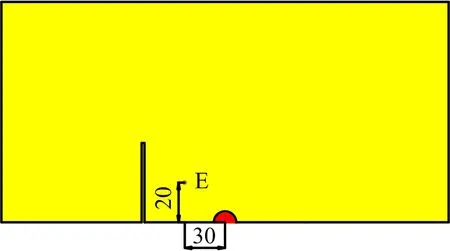
圖7 參考點E位置Fig.7 Reference point E position

利用Ls-prepost后處理軟件中的history模塊獲得不同節理寬度條件下E點的有效應力曲線,并提取曲線中的第二峰值應力大小(反射應力波產生的有效應力大小),繪制節理寬度—第二峰值有效應力曲線,結果如圖8所示。

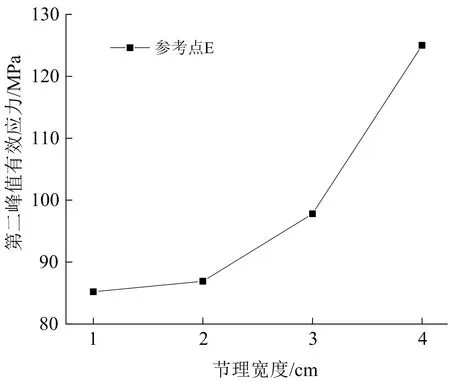
圖8 不同節理寬度條件下點E的第二峰值有效應力Fig.8 Second peak effective stress at point E under different joint width conditions

從圖8可以看出隨著節理寬度的增加,參考點E的第二峰值有效應力從85.2 MPa增大到125 MPa,與圖6中所示的炮孔與節理之間的巖體裂紋擴展范圍及損傷程度的變化趨勢一致。通過對比分析可知,隨著節理寬度的增加,爆炸應力波通過節理產生的反射拉伸應力越大,阻滯應力波的作用越明顯,導致炮孔與節理之間的巖體損傷程度及裂紋范圍增大。

3.2 節理長度對爆破裂紋擴展的影響

在相同節理寬度(1 cm)及節理位置(距炮孔中心水平距離60 cm)條件下,對比分析不同節理長度對單孔耦合爆破巖體裂紋擴展的影響。在節理長度分別為40、60、80、100 cm條件下,爆破裂紋擴展及損傷情況如圖9所示。

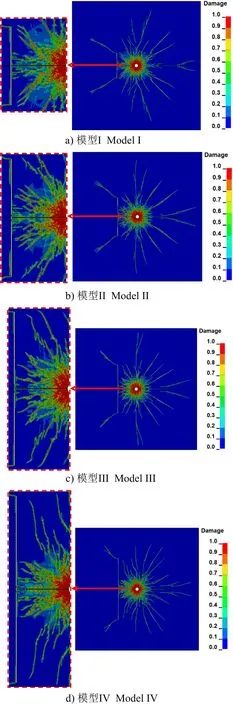
圖9 不同節理長度條件下的爆破裂紋擴展Fig.9 Explosion crack propagation under different joint length conditions

從粉碎區范圍來看,粉碎區裂紋擴展基本無變化,說明節理長度對粉碎區范圍影響也較小;節理長度的遞增導致翼裂紋擴展長度逐漸減小,節理與炮孔之間平行于節理的主裂紋長度出現遞增趨勢。

為分析節理長度對節理與炮孔之間平行于節理的裂紋擴展影響,以模型VII(節理長度100 cm)為選取參考點的基礎模型,在節理與炮孔之間中心位置平行于節理自下而上選擇等間距(20 cm)的4個參考點E、F、G、H(見圖10),繪制各參考點的有效應力時程曲線,結果如圖11所示。

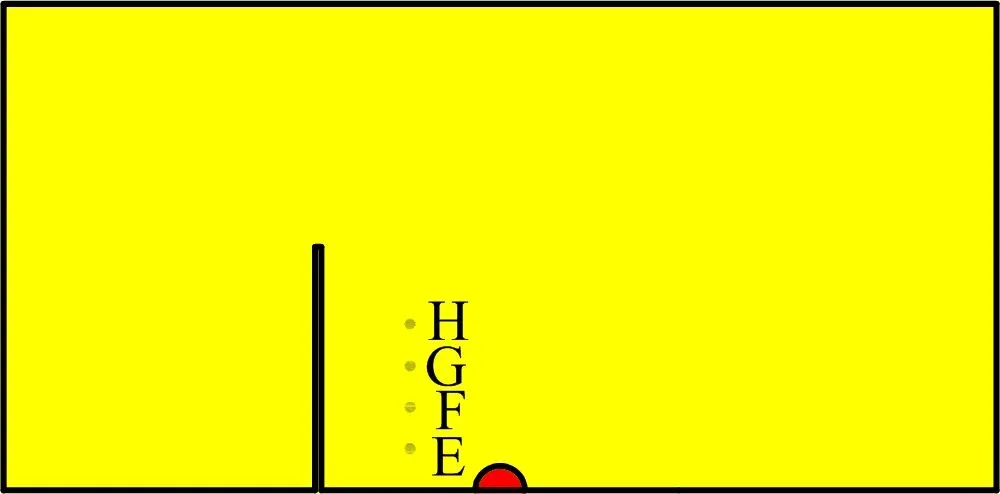
圖10 參考點E、F、G、H位置Fig.10 Reference point E, F, G, H position

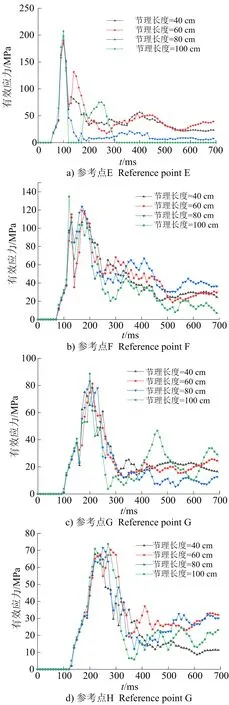
圖11 各參考點有效應力時程Fig.11 Time-history of effective stress at each reference point

由圖11可知,在相同節理長度下,隨著參考點位置的上移,爆心距的增加,參考點E、F、G、H峰值有效應力逐漸遞減,符合經典爆破理論。在相同參考點下,隨著節理長度的增加,各個參考點的峰值有效應力增加,說明節理產生的反射拉伸波與爆炸應力波共同作用促進了炮孔與節理之間平行于節理的裂紋擴展。

為進一步分析節理長度對節理端部翼裂紋長度擴展的影響,提取不同節理長度的端部有效應力數據,繪制爆破過程中節理端部的有效應力時程曲線,結果如圖12所示。

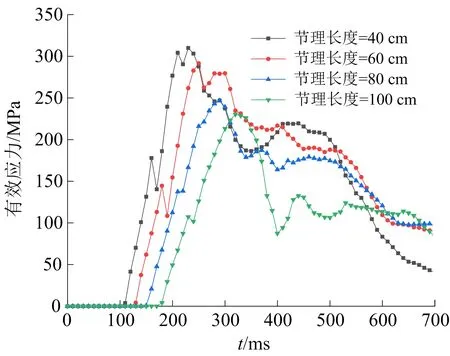
圖12 不同節理長度的端部有效應力時程Fig.12 Time-history of effective stress at the ends of different joint lengths

對比分析圖11、圖12可知,節理端部峰值有效應力明顯大于參考點E、F、G、H的峰值有效應力,說明節理的存在導致節理端部發生應力集中現象,且觀察圖12可知,隨著節理長度的增加,節理端部峰值有效應力減小,說明節理長度的增加導致節理端部應力集中現象減弱,翼裂紋擴展長度減小。

3.3 節理彎曲程度對爆破裂紋擴展的影響

在相同節理寬度、長度及位置(距炮孔中心水平距離60 cm)條件下,研究節理彎曲程度對單孔耦合裝藥爆破裂紋擴展及損傷程度的影響,在彎度0(垂直節理)、0.063、0.084、0.128的節理彎度條件下爆破裂紋擴展及損傷圖像如圖13所示。

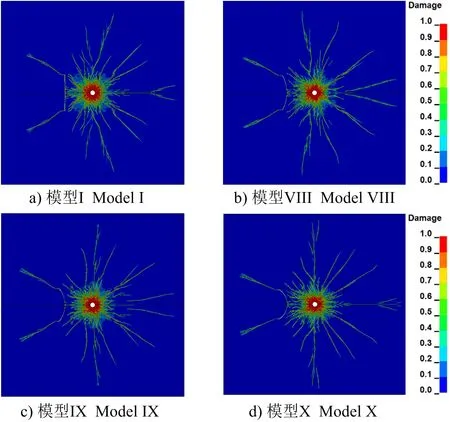
圖13 不同節理彎度條件下的爆破裂紋擴展Fig.13 Explosion crack propagation under different joint camber conditions

模擬結果顯示,節理彎度的增加對粉碎區裂紋擴展范圍及損傷程度影響仍然較小;隨著節理彎度的增加,節理左側弧形翼裂紋弧線逐漸下移,弧形翼裂紋起裂夾角(弧形翼裂紋與水平方向夾角)逐漸減小,爆生主裂紋長度逐漸增大。對4種不同節理彎度條件下,爆破產生的弧形翼裂紋長度、主裂紋長度及弧形翼裂紋起裂夾角進行統計,統計結果如表5、表6所示。

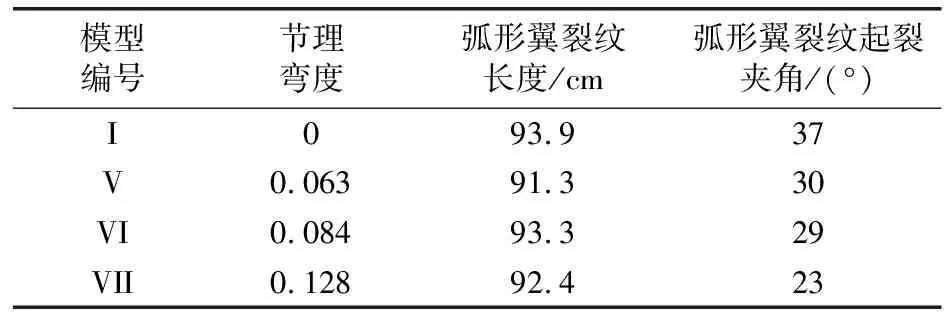
表5 不同節理彎度下弧形翼裂紋擴展長度及起裂夾角

表6 不同節理彎度下主裂紋擴展長度

由表5可知,4種不同節理彎度條件下,弧形翼裂紋長度分別為93.1、91.3、93.3、92.4 cm,弧形翼裂紋起裂夾角分別為37°、30°、29°、23°。可見,不同的節理彎度對爆生翼裂紋擴展長度及起裂夾角有不同影響,且弧形翼裂紋起裂夾角與節理彎度呈負相關。

由表6可知,節理彎度的遞增,導致平均主裂紋長度由101.9 cm遞增到127.0 cm,巖體破碎范圍增大。由此可知,節理彎度的增加對爆破裂紋擴展有促進作用。

3.4 不同節理幾何特征對爆破裂紋擴展的影響

節理的存在導致節理端部應力集中,產生翼裂紋;隨著節理的幾何特征變化,爆破裂紋擴展整體表現出復雜性與差異性,對節理與炮孔之間巖體的裂紋擴展及損傷情況影響較大,對粉碎區范圍內裂紋擴展及損傷情況影響差異較小,其原因是節理幾何特征的變化導致爆炸應力波的反射、透射和繞射的區域與強弱不同。為進一步分析不同節理幾何特征對爆破粉碎區的影響,統計3組不同模型的粉碎區半徑數值模擬結果,其結果在12.4～12.9 cm之間,可見,與無節理數值模擬驗證粉碎區半徑12.7 cm對比,節理的寬度、彎度、長度變化對粉碎區范圍內裂紋擴展及損傷情況影響較小。

4 結論

1)對于不同節理寬度,相同節理長度和位置條件下,隨著節理寬度的增加,爆炸應力波通過節理產生的反射拉伸應力越大,對應力波的阻滯作用越明顯,導致炮孔與節理之間的巖體損傷程度及裂紋擴展范圍增大。

2)對于單孔耦合裝藥爆破,在相同節理寬度條件下,隨著節理長度的增加,一方面節理產生的反射拉伸波與爆炸應力波促進炮孔與節理之間平行于節理的裂紋擴展,另一方面爆炸能量在節理中損耗增多,節理端部應力集中現象減弱,從而導致翼裂紋擴展長度減小。

3)對比分析了節理彎度從0、0.063、0.084到0.128不同彎度條件下對爆破裂紋擴展的影響,隨著節理彎度的增加,弧形翼裂紋起裂夾角逐漸減小,平均主裂紋長度逐漸增大,巖體破碎范圍增大,對爆炸應力波的阻滯作用減小,對爆破裂紋擴展有促進作用。

4)通過分析不同節理幾何特征對爆破裂紋擴展的影響,裂紋擴展總體表現出復雜性與差異性,對粉碎區范圍內裂紋擴展及損傷情況影響差異較小,對節理與炮孔之間巖體的裂紋擴展及損傷情況影響較大。