不同賦存深度下兩種巖石動力學特性對比研究

武永博,李祥龍,王建國,趙澤虎,袁芝斌

(1.昆明理工大學國土資源工程學院,昆明 650093;2.云南省教育廳爆破新技術工程研究中心,昆明650093;3.中國葛洲壩易普力公司,重慶 400020)

隨著淺部礦產的開采枯竭,深部資源開采已成必然趨勢。資料顯示,全球開采深度超千米的礦山已有100 余座,我國已有30 余座金屬礦山已超過1 000 m,深地開采已成為金屬礦業發展的重要趨勢[1]。然而在深部地下工程開挖中,不僅受爆破振動和機械開挖等外部動荷載的影響,還受到高地應力的影響[2]。隨著礦山開采深度的不斷加深,開采難度逐漸加大。因此研究不同賦存深度條件下的礦巖能耗規律及破碎分形特征,對于礦山的開采具有一定的指導意義。

利用三維動靜組合霍普金森壓桿裝置(SHPB)可以模擬深部巖石受“靜應力+擾動”的受力狀態。眾多學者利用三維SHPB動靜組合試驗裝置研究了巖石在三維應力狀態下的動力學特性,取得了豐碩成果。宮鳳強等[3]利用該裝置對砂巖試件開展了一系列的動力學試驗。研究結果表明,當圍壓不變,軸壓比在 0.52～0.87 內時,隨著軸壓的增大砂巖的抗壓強度逐步減小。周宗紅等[4]利用該裝置對白云巖的動力學特性進行了研究。結果表明當圍壓不變時,試件的變形模量隨著軸壓值的增大逐漸降低。馬少森等[5]對花崗巖進行了不同軸壓水平與圍壓水平的沖擊試驗,結果表明在軸壓增大時,花崗巖試件的單位體積吸收能逐漸降低,圍壓增大時,單位體積吸收能逐漸增大。牛勇等[6]利用該裝置對紅砂巖進行三維動靜組合加載試驗,得出試件的入射能和單位體積吸收能均與平均應變率呈正線性相關關系。殷志強等[7]用該裝置對砂巖進行了不同軸壓的沖擊試驗,同時結合能量耗散和破碎分形理論對碎塊進行了分析,得出分形維數與沖能之間存在非線性的增加關系。盧志堂等[8]研究了花崗巖在不同圍壓下的動力響應特征,發現在應變率相近情況下,花崗巖的破壞模式隨著圍壓升高由劈裂轉為壓剪破壞。王偉等[9]利用三維動靜組合加載裝置與CT掃描技術研究了砂巖的破壞機制及裂紋密度試驗,發現圍壓對于裂紋的產生與抑制作用相較于軸壓的影響更大。葉洲元等[10]研究了不同軸壓圍壓條件下細砂巖的動力學行為,發現圍壓不變時,細砂巖動靜組合強度、彈性模量隨軸向靜壓增大先升高(彈性階段)后降低(損傷階段);最大應變率和平均應變率則先下降后升高。吳越等[11]對不同軸壓與圍壓條件下砂巖進行了循環沖擊試驗,發現圍壓不變時,隨軸壓的增大,試件承受循環沖擊次數降低;軸壓不變時,循環沖擊次數隨圍壓的增加而增加。楊蒙等[12]利用該裝置研究了炭質泥巖的變形機理與吸收能變化規律。王其勝等[13]利用對花崗巖沖擊破碎后的碎塊進行了篩分試驗,得出分形維數隨應變率呈線性增長關系。

對巖石動力學特性的研究其試件大多取自同一水平巷道,而對不同賦存深度巖石的動力學特性研究較少。就爆破掘進施工而言,不同賦存深度巖石其力學特性有所差異,因此研究不同賦存深度的巖石力學性質,以尋求與炸藥波阻抗相匹配的炸藥,對于安全有效的破巖意義重大。同時就同一水平巷道而言,往往會涉及不同巖性的巖石,因此選擇大紅山銅礦2種常見的巖石,借助三維動靜加載試驗裝置,研究了兩種巖石在不同賦存深度條件下受沖擊擾動時的能量傳遞及塊度分布規律。試驗結果對于礦山安全有效開采以及爆破參數優化具有一定的指導意義。

1 三維動靜組合沖擊試驗

1.1 試件制備

試件取自大紅山銅礦掘進過程中兩種常見的巖樣(白云石大理巖、石榴黑云片巖),根據國際巖石力學與工程學會(ISRM)相關要求,將完整性和均質性較好的 2 種巖樣進行取心、切割,加工成 50 mm×50 mm 的圓柱體巖樣[14]。為了滿足 SHPB 實驗均勻性假定同時減小摩擦效應的影響,使用巖石打磨機對巖樣2個端面和四周進行打磨,控制巖樣端面不平行度和不垂直度均在 ±0.02 mm以內。加工好的部分巖石試樣如圖 1 所示。礦巖的靜態力學參數如表1所示。

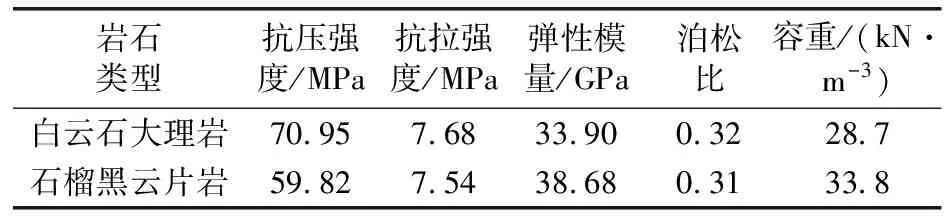
表1 基本靜力學參數

圖1 部分加工完成的礦巖試件Fig.1 Partially processed ore rock specimens

1.2 SHPB 試驗設備及基本原理

本次試驗在昆明理工大學巖石力學實驗室完成的,SHPB動靜組合加載裝置主要由充氣腔、紡錘形子彈、壓桿系統、軸壓加載系統、圍壓加載系統和數據采集系統等組成。壓桿系統由入射桿和透射桿組成,入射桿長度為2 000 mm,透射桿的長度為1 500 mm,直徑均為20 mm,彈性模量為210 GPa。試驗裝置圖2所示,紡錘形子彈撞擊入射桿時,會在入射桿中產生半弦波,可以實現恒應變率的加載[15]。

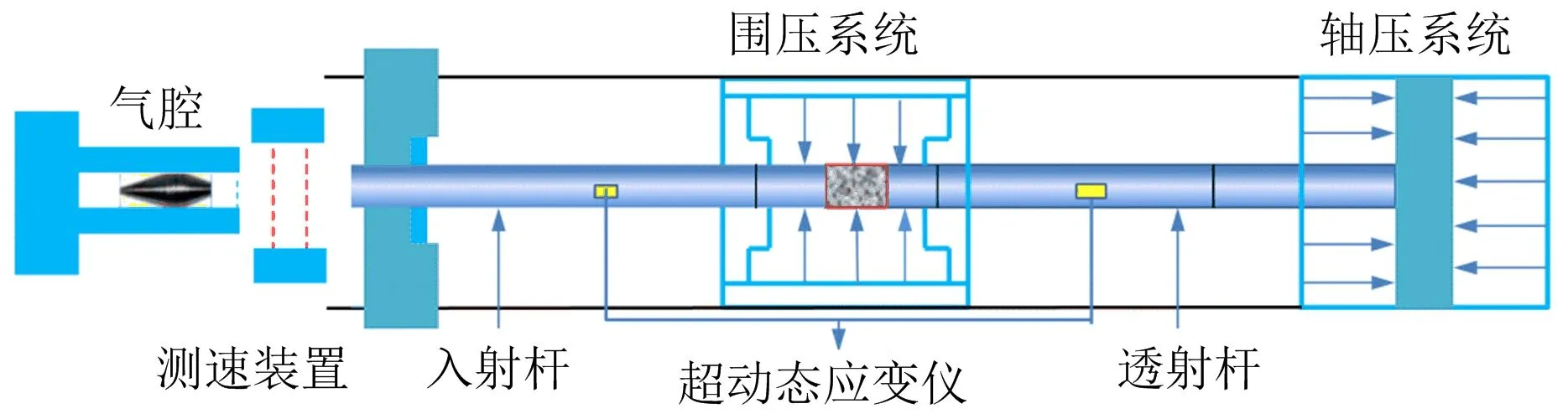
圖2 三維動靜組合加載系統Fig.2 Three-dimensional dynamic and static combined loading system

SHPB 試驗是基于一維應力波的傳播理論,當子彈以一定的沖擊速度撞擊入射桿時,會在入射桿中產生應力脈沖。當入射桿中的應力脈沖傳播至入射桿與巖石試件的交界面時,由于巖石與入射桿之間的波阻抗的差異,應力波會在異質界面發生透射與反射,一部分應力波被反射回入射桿中形成反射波,另一部分穿過試件在透射桿中形成透射波。入射波、反射波、透射波通過粘貼在壓桿上的應變片測得。采用三波法,可得到巖石的動態應力應變關系。

1.3 實驗方案

為使試驗中試樣受力狀態貼合現場,與井下實際應力環境相匹配,根據大紅山礦區(500～1 000 m)地壓監測結果,確定試驗選擇的軸壓與圍壓。當賦存深度分別為500、600、700、800、900、1 000 m時,測得的軸壓為30、35、40、47、53、59 MPa,圍壓為:14、16、19、22、24、27 MPa。試驗過程中先施加圍壓,后施加軸壓。經預實驗測試,當沖擊氣壓為1.6 MPa時,巖石試件破碎且破碎塊度較為均勻,因此選擇1.6 MPa作為試驗的沖擊氣壓。

2 結果分析

2.1 礦巖動態力學影響規律

巖石在三維動靜組合加載下的峰值應力與賦存深度之間的關系如圖3所示。

圖3 賦存深度與峰值應力之間的定量關系Fig.3 Quantitative relationship between occurrence depth and peak stress

在三維動靜組合加載條件下,隨著賦存深度的增大,白云石大理巖和石榴黑云片巖的峰值應力均呈線性增加趨勢,相關系數分別為0.96和0.90。分析認為,巖石內部隨機分布大量的微裂隙或缺陷,軸壓與圍壓能使微裂紋發生閉合或壓密,提高了試件整體的密實度,進而抑制材料的劣化,使得巖石峰值應力增大。

2.2 能量分配規律

試件裂紋的產萌生、擴展、匯集都是能量交換和釋放的結果,在巖石變形破壞的整個過程中都會涉及到能量的變化。因此可以從能量的角度來分析試件的變形破壞意義重大。為了分析不同賦存深度下的白云石大理巖和石榴黑云片巖能量的傳遞規律,計算了不同賦存深度下礦巖的能量參數。繪制了2種礦巖的各能量占比柱狀圖,如圖4所示。可知,對于不同賦存深度下的白云石大理巖,當賦存深度在500～1 000 m時,反射能占比從16.22%減少至11.16%,透射能占比從70.20%增加至78.98%,吸收能占比從13.58%。可以看出吸收能的占比最小,說明賦存深度值越大,礦巖吸收能占比在降低,礦巖越難破碎。對于石榴黑云片巖,反射能占比從22.96%減少至15.50%,透射能占比從59.37%增加至70.95%,吸收能占比從17.67%減少至13.54%。綜上,白云石大理巖和石榴黑云片巖透射能占比在59.37%至78.98%之間,均大于反射能占比與吸收能占比,而吸收能占比在9.86%至17.67%之間,表明隨著賦存深度的增加,能量更多的以反射波和透射波形式消散。

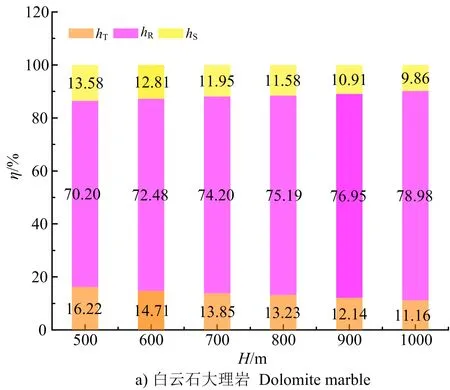
圖4 不同賦存深度下各能量分布Fig.4 Energy distribution at different depths

巖石破碎吸收的能量與試件體積密切相關,吸能密度更能反映試件破碎過程中吸收能量情況。為了分析吸能密度與賦存深度之間的關系,繪制了2種礦巖吸能密度與賦存深度之間的散點圖,并進行擬合,如圖5所示。可以看出,兩種礦巖的吸能密度隨賦存深度的增加呈線性減少關系。當賦存深度逐漸增加時,白云石大理巖當的吸能密度值由1.14 J/cm3逐漸降為0.84 J/cm3,石榴黑云片巖的吸能密度值由1.49 J/cm3逐漸降為1.15 J/cm3,這主要是由于隨著賦存深度的增加,試件在動態沖擊荷載作用下側向變形時,所受到的約束力增大,裂紋擴展的速度受到的限制越大,裂紋擴展緩慢,因此試件吸收的能量逐漸降低。

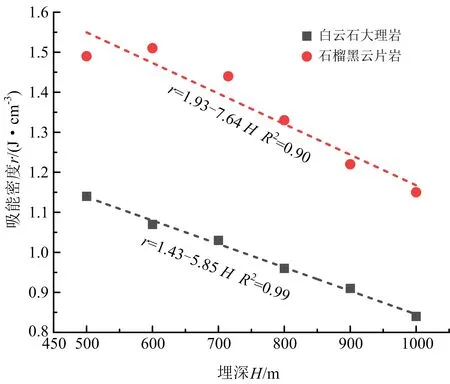
圖5 吸能密度與賦存深度之間的關系Fig.5 Relationship between energy absorption density and occurrence depth

3 試件破碎分形研究

3.1 沖擊破碎形態分析

不同賦存深度的礦巖受到一定的沖擊作用后,其破碎后碎塊的直徑和形狀會有所不同。不同賦存深度下的礦巖試件受沖擊破壞后形成的碎塊如圖6所示。可以看出,在相同沖擊氣壓下,2種礦巖隨著賦存深度的增加(500～1 000 m),大塊率明顯增加,細小顆粒狀及粉末狀明顯減少。從破壞程度來講,同一賦存深度條件下,石榴黑云片巖比白云石大理巖更容易破壞,且碎塊數量更多。導致其細小顆粒或粉末狀減少的原因是,在施加6種等級的靜載條件下,均未達到礦巖的單軸抗壓強度,隨著賦存深度的不斷增加,礦巖內部存在的微裂隙被不斷壓實壓密,因此在相同沖擊氣壓下,礦巖沿裂隙的變形變小,從破碎的形態上看,塊狀增加,顆粒狀與粉末狀減少。

圖6 不同賦存深度下礦巖破碎形態Fig.6 Fracture morphology of ore rock under different occurrence depths

3.2 分形維數計算

謝和平等[16]將分形理論引入了巖石的破壞中,認為巖石宏觀破碎是其內部微裂紋或缺陷不斷萌生、發育、匯集和貫通的最終結果,從細觀損傷到宏觀破碎的發展過程也是能量耗散過程,并具有分形性質。根據篩分的質量和頻率間的關系,得到沖擊破碎后碎塊分布的方程式(1):

Y=M(x)/M(T)=(x/xm)3-D

(1)

式中:M(x)為碎塊直徑小于x對應的質量;M(T)為篩下碎塊的總質量;x為沖擊破碎后碎塊的直徑;xm為篩分礦巖碎塊的最大直徑,對式(1)取雙對數,得到式(2):

lgY=lg[M(x)/M(T)]=(3-D)lg(x/xm)

(2)

在lg[M(x)/M(T)]-lgx雙對數圖中,采用最小二乘法對其線性擬合,得到如圖7所示的擬合圖,每條擬合直線的斜率為b=3-D,由斜率b即可計算出相應的分形維數D。

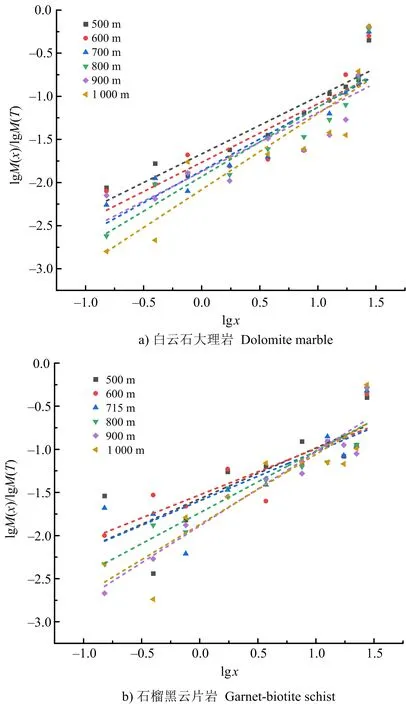
圖7 雙對數累積粒度特征曲線Fig.7 The curve of total logarithmic cumulative particle size

由圖7說明,無論是白云石大理巖還是石榴黑云片巖,其lg[M(x)/M(T)]與lgx具有良好的線性相關性,說明了在一定沖擊氣壓沖擊后,不同賦存深度的巖石的破碎塊度分布具有較好的自相似特征,也說明兩種礦巖的沖擊破碎塊度符合分形規律。為了直觀分析分形維數與賦存深度之間的關系,繪制了將分形維數與賦存深度之間的散點圖,并進行擬合,如圖8所示。可得,三維動靜組合加載條件下,在試驗范內,兩種礦巖分形維數與存深度之間呈線性減小的關系,相關系數均在0.8以上。賦存深度在500～1000 m內時,白云石大理巖分形維數分別由2.34降至2.12,降低了9.4%;石榴黑云片巖由2.42降至2.18,降低了9.9%。以此說明在三維動靜組合加載條件下,石榴黑云片巖在沖擊破壞過程中破碎程度與白云石大理巖相比更為明顯。

圖8 礦巖的分形維數與賦存深度之間的關系Fig.8 The relationship between fractal dimension of ore rock and occurrence depth

4 結論

1)白云石大理巖和石榴黑云片巖在沖擊荷載作用下的峰值應力隨賦存深度變化規律基本一致,在試驗范圍內,均隨賦存深度的增大呈正相關關系。

2)兩種礦巖的能量傳遞規律與埋深關系密切,當沖擊氣壓一定,礦巖吸收能和反射能隨賦存深度的增加(500～1 000 m)逐漸減小,透射能隨賦存深度的增加逐漸增加,吸能密度隨賦存深度的增加而減小。

3)兩種礦巖的破壞形態大體相同,在相同沖擊氣壓下,隨著埋深的不斷增加,礦巖破碎的大塊增加,粉碎顆粒減少,石榴云母片巖相比于白云石大理巖破碎程度更大。

4)隨著賦存深度的增加,兩種礦巖的分形維數線性減小。當埋深從500 m增至1 000 m時,白云石大理巖的分形維數從2.34減至2.12,石榴黑云片巖的分形維數從2.42減至2.18,白云石大理巖分形維數受賦存深度影響比石榴黑云片巖更明顯。