利用韋爾伯福斯擺測量彈簧材料的泊松比
藍亦青,李濱旭,張天旭,張廷德,龍 象,王曉峰,何春清,劉海林
(武漢大學 物理科學與技術學院,湖北 武漢 430072)
泊松比是指材料在單向受拉或受壓時,橫向正應變與軸向正應變的比值,也叫橫向變形系數. 泊松比是反映材料橫向變形的彈性常量. 測量固體材料泊松比的方法主要為直接測出微小的橫向正應變與軸向正應變進而得到泊松比,包括聲測法[1]、光測法[2]、電測法[3]等,上述方法的本質是使用傳感器高精度測量微小形變. 如果將材料制成彈簧,通過分析彈簧的相關參量可以測得彈簧材料的泊松比. 由于彈簧材料泊松比的測定較為復雜,很難精確測量所需參量,因此在實驗中,嘗試通過臨界條件將難以準確測量的彈簧材料參量轉化為容易測量的韋爾伯福斯擺(簡稱韋氏擺)的運動參量[4].
1 實驗裝置
實驗器材:彈簧(內直徑d1=1.748 cm,外直徑d2=1.912 cm)、韋氏擺擺錘、螺母若干(厚度d=0.300 cm,質量m0=0.700 g)、光學面包板、超聲波距離傳感器、光電門、PASCO-850通用接口、電磁鐵、直流電源、PASCO Capstone軟件.
1.1 韋氏擺
韋氏擺的擺錘以3D打印的PLA塑料為主體,與橫向、縱向2個金屬螺柱組裝而成,如圖1所示. 在豎直方向增減螺母的數量可以改變擺錘的質量,沿水平方向螺柱移動螺母可以改變擺錘的轉動慣量,且可通過標尺讀出螺母的位置,計算轉動慣量.

圖1 韋氏擺
1.2 超聲波距離傳感器
由PASCO-850通用接口連接超聲波距離傳感器和電腦. 利用Capstone程序,實時測出擺錘底端與傳感器的距離,并且自動在Capstone界面中作出z-t曲線.
1.3 光電門
由PASCO-850通用接口連接光電門和電腦. 利用Capstone程序,實時測出橫向螺柱經過光電門時的速度,并作出v-t曲線.
1.4 儀器組裝與軟件初始化
實驗裝置如圖2所示.

圖2 實驗裝置圖
1)連接彈簧與擺錘,分別將2個螺母對稱旋入水平螺柱的兩端.
2)連接電磁鐵與直流電源,斷開開關.
3)通過PASCO-850通用接口連接光電門、超聲波距離傳感器與電腦.
4)打開Capstone軟件,設置距離傳感器為近距離模式,設置采樣頻率為50 Hz.
5)將韋氏擺、光電門、電磁鐵固定到鐵架臺上,并將引導桿固定到電磁鐵的鐵架臺旁邊.
為了保證在運動過程中韋氏擺時刻滿足運動方程,在擺放時應注意:
1)盡量由靜止豎直釋放韋氏擺. 將超聲波距離傳感器放置在電磁鐵正下方.
2)放置光電門時,要盡量保證擺在平衡位置時水平螺柱、轉軸與光電門共平面(光電門的指示燈常亮).
3)使用超聲波傳感器測距離時,傳感器和擺的距離保持在40 cm左右.
2 實驗原理
將韋氏擺的擺錘提升或者拉離平衡位置后,由靜止釋放,擺錘沿垂直線上下振蕩,并且將豎直振動模式的部分動能緩慢地轉換為水平扭轉模式的動能,當水平的擺動幅度達到最大值后,這部分能量又由水平扭轉模式轉換回豎直振動模式. 如果將橫向螺柱上的螺母調整到適當位置,使豎直振動模式和水平扭轉模式的頻率相同時,則動能在這2種振蕩模式之間完全來回傳遞,即豎直方向的振動會出現停止的情況,反之,當豎直方向振子振動最強時其水平扭轉運動也幾乎停止.
2.1 韋氏擺的一般運動規律
對于一般的螺旋彈簧,彈簧在豎直伸縮過程中,可以利用勁度系數k表示彈簧的彈性勢能.與此同時,彈簧下端會隨著彈簧的拉伸而轉動,彈簧下端偏離平衡位置的轉角φ與彈簧伸長量z成正比[5],比例系數為C,即
φ(z)=Cz,
(1)
彈簧轉動時產生扭矩,勢能為
(2)
其中D為彈簧扭轉系數.
對系統進行能量分析,拉格朗日函數[6]為
(3)

(4)
因DC2?k,以下討論與計算均令k′≈k.通解為
z=A1eiω1t+A2e-iω1t+A3eiω2t+A4e-iω2t,
(5)
其中
(6)
(7)
(8)
(9)
2.2 韋氏擺的共振機理
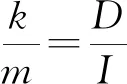
(10)
(11)
此時水平和豎直方向的振動都可以降為0,出現明顯的能量轉換現象,或者說“完全”共振現象,即水平扭轉運動最強時豎直振動幾乎停止;反之,當豎直方向振子振動最強時其水平扭轉運動幾乎停止.
接下來分析耦合運動的周期.實驗共有3個周期量,分別為豎直方向小幅振動周期、水平方向小幅轉動周期以及二者都表現的拍周期[7].拍的周期為
(12)
式(6)~(7)變換為
(13)
實驗中唯一改變的量是轉動慣量,因此將(ω1-ω2)2看作轉動慣量I的單變量函數,尋找極值條件.
(14)
進而得到
(15)
此時
拍周期T達到最大值,同時擺也達到完全共振的狀態.由式(6)、式(7)以及式(3),利用Matlab進行數值計算,可以得到給定的擺錘振子具有不同轉動慣量情況時拍周期的變化曲線,如圖3所示.
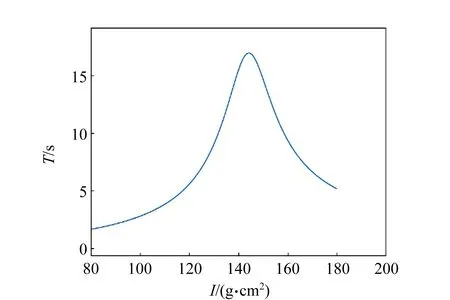
圖3 Matlab計算的T-I關系
在振子的轉動慣量由80.000 g·cm2增加到約143.000 g·cm2的過程中,拍周期T增加并達到最大值,當轉動慣量繼續增大則T減小,模擬結果與理論預測一致.
2.3 測量彈簧材料的泊松比
對于一般的螺旋彈簧,其參量滿足[8-9]
D=kR2(1+σcos2α),
(16)
其中,k為彈簧的勁度系數,R為彈簧的半徑,σ為金屬的泊松比,α為彈簧的螺旋角.
由于實驗使用的彈簧為拉簧,即使在懸掛伸長后,α?1,故cos2α≈1,式(16)可以變為
D=kR2(1+σ).
(17)
因此,當拍周期達到最大時即擺達到完全共振時,將式(17)代入式(15),得到金屬的泊松比為
(18)
其中,I為系統的有效轉動慣量,由平行軸定理可以得到
(19)
其中r為螺母距離轉軸的位置.等式右邊的第2項為螺母對中心軸的額外轉動慣量.
調節擺的轉動慣量并釋放擺,觀察擺接近完全共振的現象,之后在其對應的螺母位置處附近選若干點,改變位置進行實驗測量,得出拍周期最大時對應的轉動慣量,利用式(18)即可測出彈簧材料的泊松比.
2.4 韋氏擺的阻尼研究
實際實驗存在阻尼,因此可以在方程(4)中加入阻尼項,
(20)
其中,β1和β2為韋氏擺在豎直、水平方向運動的阻尼系數.
無法求得方程(20)的解析解,使用Matlab對方程進行數值求解,可以得到有、無阻尼時,擺錘高度隨時間的變化規律,如圖4所示.
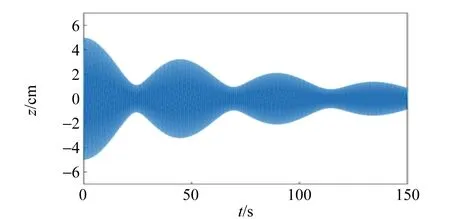
(a)有阻尼
由圖4可知:當存在阻尼時擺振子的振幅隨時間衰減,但拍周期與是否存在阻尼無關.
3 實驗方法及結果
3.1 初步調節韋氏擺并觀察擺的耦合特點
1)將韋氏擺靜置,上移電磁鐵使其緊貼擺下端但不與擺相碰. 閉合電路開關,電磁鐵吸住韋氏擺,利用引導柱下拉電磁鐵至適當位置,調整韋氏擺的擺角位置,使其與平衡位置時的擺角方向相同,撤去引導柱.
2)打開距離傳感器,斷開電磁鐵開關,在釋放彈簧后,固定轉動電磁鐵(防止電磁鐵影響距離傳感器的測量結果). 觀察韋氏擺的運動模式,可以看到擺錘逐漸出現水平轉動現象.
3)固定1對螺母,對稱調節另1對螺母的位置,重復步驟1)和2),直至豎直方向振動出現基本停止.
4)再次通過電腦記錄數據,實時觀測韋氏擺豎直方向振動距離隨時間的變化曲線,以及水平旋轉速度隨時間的變化曲線. 觀察豎直、水平方向振動的拍現象.
將螺母與轉軸的距離x1和x2作為可調參量,改變擺體的轉動慣量,見表1. 不改變其他參量,系統總轉動慣量在141.000~147.000 g·cm2的區間內逐步改變,并測量擺上2個固定點的水平轉動線速度和豎直位置,如圖5所示. 容易觀察到如上所述“共振”,水平轉動和豎直振動都出現了拍現象. 如圖6所示,在有阻尼情形韋氏擺豎直位置隨時間變化的Matlab模擬結果和實驗結果一致.

表1 轉動慣量I、水平轉動停止時間間隔Ti及拍周期T
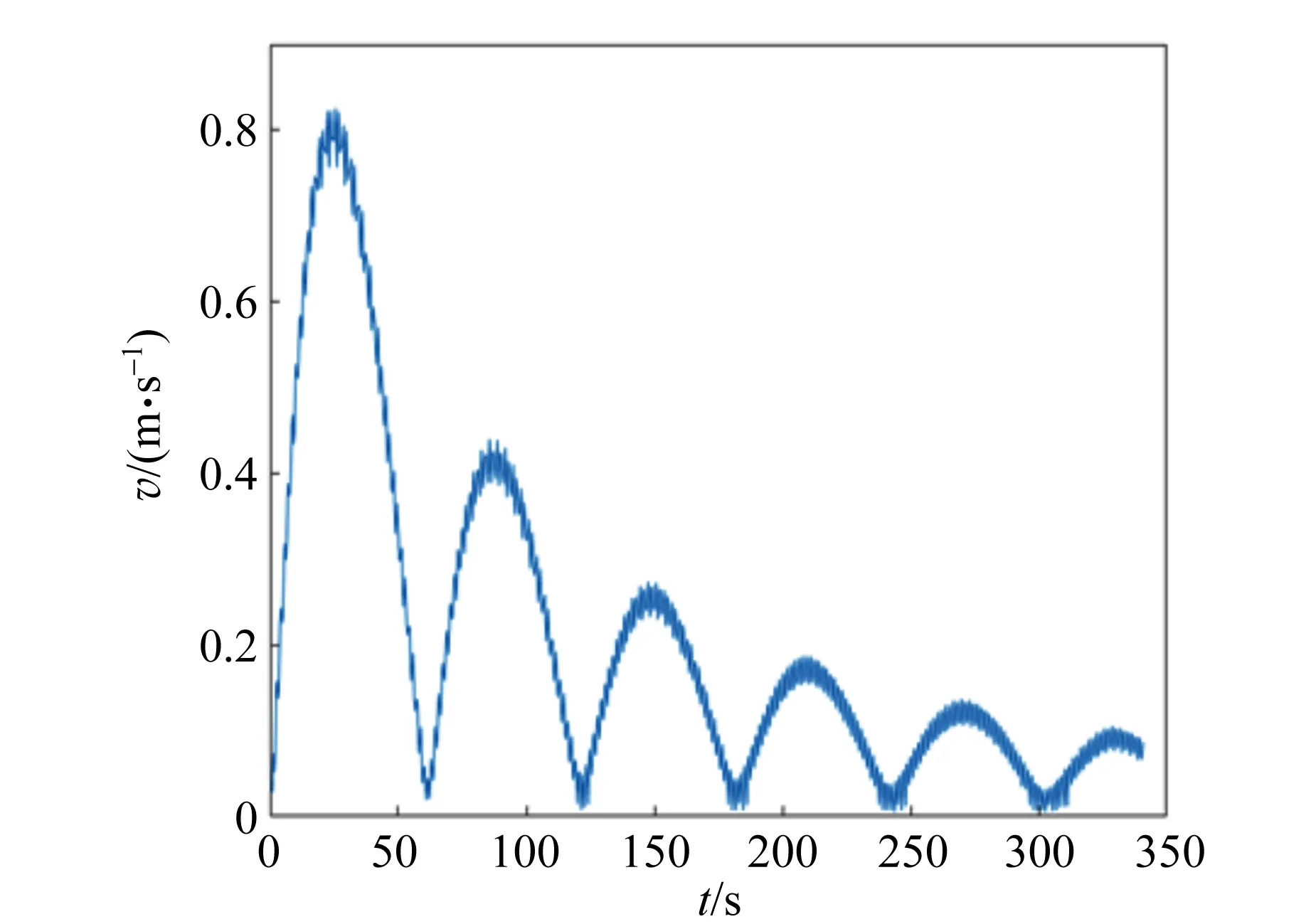
(a)水平線速度
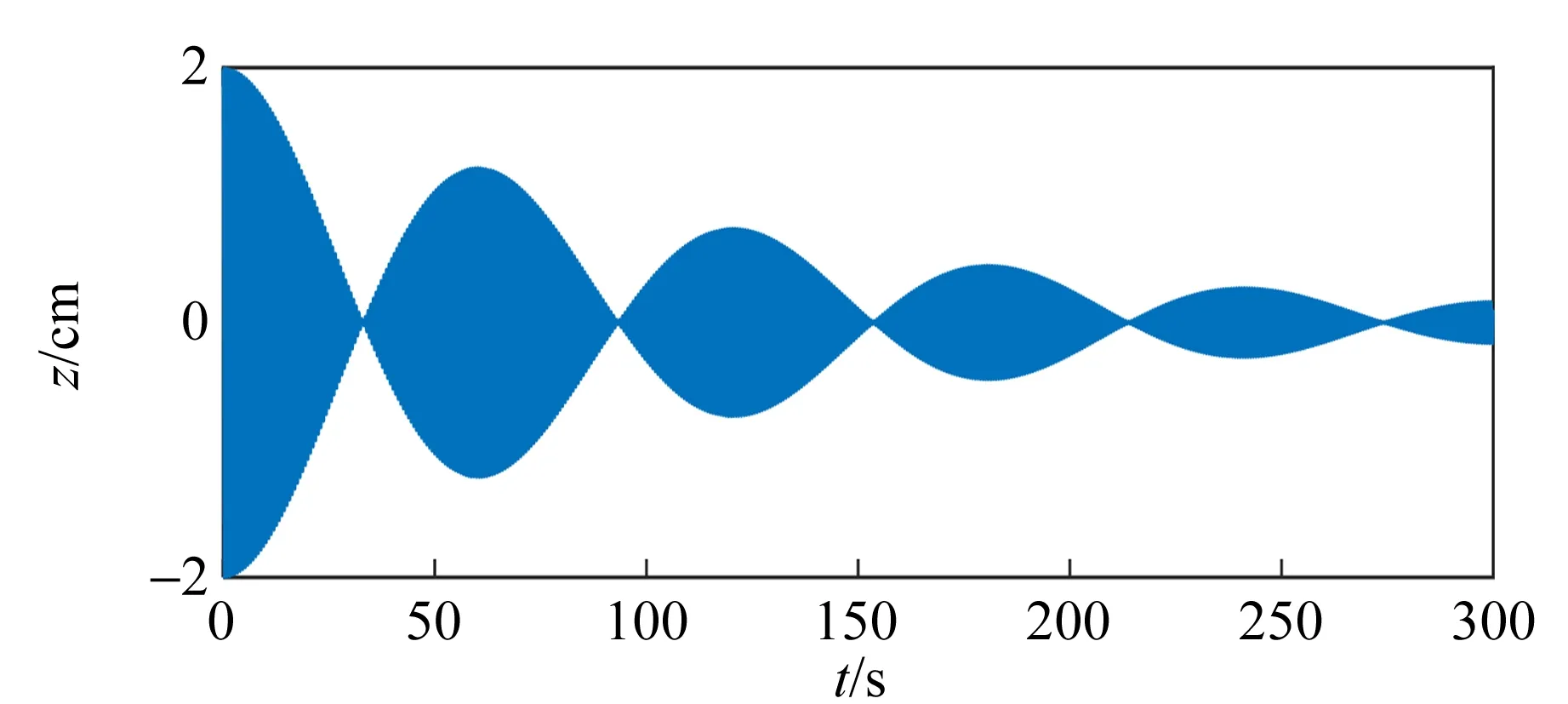
(a)模擬
3.2 微調韋氏擺并測定彈簧材料的泊松比
1)在粗調韋氏擺的基礎上,對稱改變兩螺母位置并記錄外側位置,使螺母位置在共振位置附近取值,并進行3.1的步驟1)和2),根據數據得到連續5個拍的開始、結束時間T1,T2,T3,T4,T5和T6.
2)通過微調自制韋氏擺螺母位置改變其轉動慣量.由式(19)計算螺母處于不同位置時的轉動慣量I,實驗上獲得不同轉動慣量韋氏擺對應的共振曲線.從共振曲線中順序讀出第i個最小位移出現的時刻Ti,直線擬合時間Ti與順序i之間的關系,即可得到不同轉動慣量對應的拍周期T.最后,作出拍周期T與轉動慣量I的關系曲線,如圖7所示.
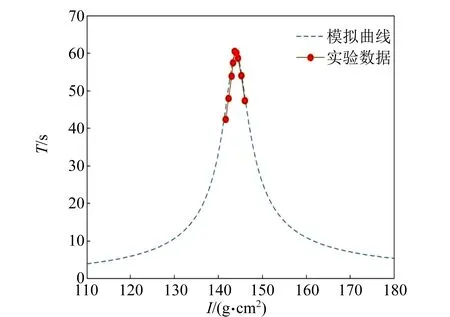
圖7 韋氏擺的T-I曲線
由擬合結果易知,當拍周期T達到最大時,對應的轉動慣量I=143.850 g·cm2. 利用式(18)計算金屬彈簧的泊松比σ=0.274 5,不確定度uσ=0.01,則σ=0.27±0.01.
另外,當彈簧參量取值為C=0.85 m-1,D=1.744×10-3N·m時,拍周期隨轉動慣量變化的數值模擬與實驗結果一致(見圖7). 由T-I模擬曲線得出拍周期T達到最大時,對應的轉動慣量I=143.900 g·cm2,計算結果與實驗測量一致.
4 結束語
耦合現象是力學中的獨特現象,展現了結構力學的內在機理. 本次實驗,實驗儀器簡單,利用擺錘可以靈活地調節轉動慣量,方便實驗操作. 由于其獨特的耦合振動現象,在了解單個方向的運動狀態后可以得到整體系統的拍周期,在實驗儀器缺失的情況下,可以測量單方向運動達到實驗目的. 該實驗可以作為普通物理實驗,不僅能夠觀察到耦合振動現象,又能借助韋氏擺巧妙設計泊松比的力學測量方法.

