一種改進(jìn)的爬行動(dòng)物搜索算法

杜興麗 劉玲 袁平

摘要：針對(duì)爬行動(dòng)物搜索算法存在早熟收斂、易陷入局部最優(yōu)等問(wèn)題，提出一種改進(jìn)的爬行動(dòng)物搜索算法（LERSA）。通過(guò)精英反向?qū)W習(xí)策略提高初始種群的質(zhì)量，在種群位置更新求解適應(yīng)度值的過(guò)程中加入Levy飛行策略對(duì)種群中個(gè)體位置進(jìn)行更新，結(jié)合非線性加權(quán)策略改良控制參數(shù)平衡RSA算法的全局搜索與局部搜索能力。使用公開(kāi)的性能驗(yàn)證函數(shù)、秩和檢驗(yàn)及三桿桁架問(wèn)題進(jìn)行算法性能測(cè)試，結(jié)果表明改進(jìn)后的算法具有良好的尋優(yōu)性能，能有效解決工程優(yōu)化問(wèn)題。

關(guān)鍵詞：爬行動(dòng)物搜索算法 精英反向?qū)W習(xí) Levy飛行 非線性加權(quán)策略

中圖分類號(hào)：T391文獻(xiàn)標(biāo)志碼：A文章編號(hào)：1671-8755（2023）03-0082-07

An Improved Reptile Search Algorithm

DU Xingli1， LIU Ling2， YUAN Ping1

（1. School of Computer Science and Technology， Southwest University of Science and Technology，

Mianyang 621010， Sichuan， China; 2. Educational Informationization Office， Southwest University

of Science and Technology， Mianyang 621010， Sichuan， China）

Abstract：? An improved reptile search algorithm （LERSA） was proposed to address the problems of premature convergence and easy falling into local optimum in reptile search algorithm. The elite oppositionbased learning strategy was used to improve the quality of the initial population， the Levy flight strategy was added to update the individual positions in the population during the process of fitness value solution for population position update， and the nonlinear weighting strategy was combined to improve the control parameters to balance the global search and local search ability of RSA algorithm. The algorithm performance test was carried out by using the public performance verification function， rank sum test， and threebar truss problem. The results show that the improved algorithm has good optimization performance and can effectively solve engineering optimization problems.

Keywords：? Reptile search algorithm; Elite oppositionbased learning; Levy flight; Nonlinear weighting strategy

元啟發(fā)式算法結(jié)合了隨機(jī)算法和局部搜索算法的優(yōu)勢(shì)，具有較出色的搜索性能。爬行動(dòng)物搜索算法（Reptile search algorithm，RSA）是Abualigah等受鱷魚(yú)狩獵行為啟發(fā)提出的一種新的元啟發(fā)式算法［1］。RSA相較于蝗蟲(chóng)優(yōu)化算法（Grasshopper optimization algorithm， GOA）［2］、灰狼優(yōu)化算法（Grey wolf optimizer， GWO）［3］、海洋捕食者算法（Marine predators algorithm， MPA）［4］和樽海鞘優(yōu)化算法（Salp swarm algorithm， SSA）［5］具有更好的全局搜索性能。

Almotairi等［6］將RSA算法與鮣魚(yú)優(yōu)化算法（Remora optimization algorithm， ROA）［7］相結(jié)合，使用均值轉(zhuǎn)移策略來(lái)調(diào)控算法的搜索性能，解決RSA算法全局搜索與局部搜索不平衡的問(wèn)題。Shinawi等［8］將RSA算法與自適應(yīng)神經(jīng)模糊推理系統(tǒng)（Adaptive neurofuzzy inference system， ANFIS）相結(jié)合，用于巖土的膨脹潛力預(yù)測(cè)。付華等［9］針對(duì)該算法的缺陷，使用水波進(jìn)化和動(dòng)態(tài)萊維飛行進(jìn)行改進(jìn)。李新華等［10］構(gòu)建WPD-RSA-ELM模型進(jìn)行水文時(shí)間序列多步預(yù)測(cè)。Ekinci等［11］提出基于萊維飛行的爬行動(dòng)物搜索算法解決電力系統(tǒng)工程設(shè)計(jì)問(wèn)題。Huang等［12］提出基于Levy飛行和交互式交叉策略的爬行動(dòng)物搜索算法。

從已有的研究中發(fā)現(xiàn)，RSA算法所需調(diào)節(jié)參數(shù)少，易于實(shí)現(xiàn)，拓展了優(yōu)化問(wèn)題的解決方案。但RSA算法仍存在早熟收斂、尋優(yōu)精度低和易陷入局部最優(yōu)的問(wèn)題［9］，算法局部搜索能力和全局搜索能力需要更好平衡［7］。針對(duì)前述問(wèn)題，本文提出了一種改進(jìn)的爬行動(dòng)物搜索算法（Reptile search algorithm combining Levy flight and elite oppositionbased learning，LERSA），以期為工程優(yōu)化問(wèn)題提供更好的解決方案。

1爬行動(dòng)物搜索算法

RSA算法核心包含2個(gè)階段：圍捕階段和狩獵階段。圍捕階段的策略是高空行走和腹部行走，負(fù)責(zé)全局搜索；狩獵階段的策略是協(xié)調(diào)狩獵和合作狩獵，負(fù)責(zé)局部勘探。

當(dāng)tT2時(shí)，進(jìn)行全局搜索，數(shù)學(xué)表達(dá)式如下：

xt+1i，j=Besttj-ηti，j×β-Rti，j×rand，tT4（1）

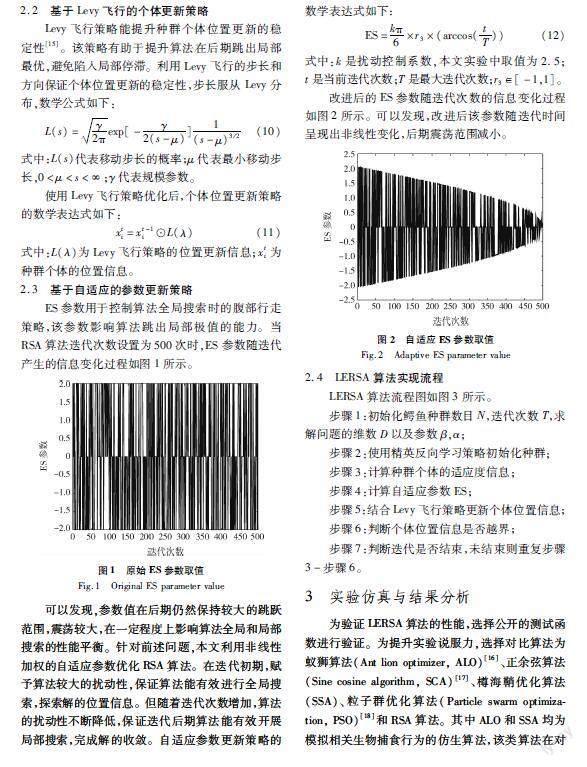
xt+1i，j=Besttj×xr1，j×ES×rand，T4

當(dāng)t>T2時(shí)，進(jìn)行局部勘探，數(shù)學(xué)表達(dá)式如下：

xt+1i，j=Besttj×Pti，j×rand，T2

xt+1i，j=Besttj-ηti，j×ε-Rti，j×rand，t>3T4（4）

式中：Besttj是當(dāng)前迭代的最優(yōu)位置；rand∈［0，1］；r1∈［1，N］，N是候選解總數(shù)；ES=2×r3×（1-tT），r3∈［-1，1］，t是當(dāng)前迭代次數(shù)，T是最大迭代次數(shù)；ηi，j=Besttj×Pi，j是第 i 個(gè)種群個(gè)體第 j 維的狩獵算子；Pi，j是最佳解與當(dāng)前解在第j維位置的百分比，β是敏感系數(shù)；Ri，j是縮減函數(shù)，數(shù)學(xué)表達(dá)式如下：

Pi，j=α+xi，j-MxiBesttj×（Bj，u-Bj，l）+ε（5）

Mxi=1nnj=1xi，j（6）

Ri，j=Besttj-xr2，jBesttj+ε（7）

式中：ε是很小的正數(shù)；Mxi是候選解的平均位置；Bj，u與Bj，l是j維的上下界；α是敏感參數(shù)；r2∈［1，N］。

ES參數(shù)通過(guò)調(diào)節(jié)圍捕階段全局搜索的步長(zhǎng)跳躍程度在一定程度上平衡算法的全局搜索和局部搜索。

2LERSA算法

LERSA算法的基本思路為：利用精英反向?qū)W習(xí)策略構(gòu)建初始種群，提升初始種群的質(zhì)量；利用Levy飛行策略改良種群個(gè)體的位置變更策略，增強(qiáng)RSA算法的局部搜索能力，讓算法更好跳出局部最優(yōu)；結(jié)合非線性加權(quán)策略，改良控制參數(shù)，平衡RSA算法的全局搜索與局部搜索能力。

2.1基于精英反向種群的初始化策略

精英反向種群初始化策略同時(shí)搜索當(dāng)前解和動(dòng)態(tài)反向?qū)W習(xí)的解，并選擇保存更優(yōu)的解［13］。本文使用精英反向?qū)W習(xí)構(gòu)造反向種群［14］，并從候選解和反向候選解中選取最優(yōu)解，使生成的候選解包含更多有效信息。該策略代替原算法的隨機(jī)生成初始種群的方法，有助于提升算法初始種群質(zhì)量，避免初始盲目搜索。

D維空間中精英xi的數(shù)學(xué)表達(dá)式如下：

xi=［xi，1，xi，2，…xi，D］（8）

種群精英反向解x—i，j的數(shù)學(xué)表達(dá)式如下：

x—i，j=r（bj，l+bj，u）-xi，j（9）

式中：xi，j是種群的個(gè)體信息；bj，l是種群的下邊界；bj，u是種群的上邊界。

2.2基于Levy飛行的個(gè)體更新策略

Levy飛行策略能提升種群個(gè)體位置更新的穩(wěn)定性［15］。該策略有助于提升算法在后期跳出局部最優(yōu)，避免陷入局部停滯。利用Levy飛行的步長(zhǎng)和方向保證個(gè)體位置更新的穩(wěn)定性，步長(zhǎng)服從Levy分布，數(shù)學(xué)公式如下：

L（s）=γ2πexp［-γ2（s-μ）］1（s-μ）3/2（10）

式中：L（s）代表移動(dòng)步長(zhǎng)的概率；μ代表最小移動(dòng)步長(zhǎng)，0<μ

使用Levy飛行策略優(yōu)化后，個(gè)體位置更新策略的數(shù)學(xué)表達(dá)式如下：

xti=xt-1i⊙L（λ）（11）

式中：L（λ）為L(zhǎng)evy飛行策略的位置更新信息；xti為種群個(gè)體的位置信息。

2.3基于自適應(yīng)的參數(shù)更新策略

ES參數(shù)用于控制算法全局搜索時(shí)的腹部行走策略，該參數(shù)影響算法跳出局部極值的能力。當(dāng)RSA算法迭代次數(shù)設(shè)置為500次時(shí)，ES參數(shù)隨迭代產(chǎn)生的信息變化過(guò)程如圖1所示。

可以發(fā)現(xiàn)，參數(shù)值在后期仍然保持較大的跳躍范圍，震蕩較大，在一定程度上影響算法全局和局部搜索的性能平衡。針對(duì)前述問(wèn)題，本文利用非線性加權(quán)的自適應(yīng)參數(shù)優(yōu)化RSA算法。在迭代初期，賦予算法較大的擾動(dòng)性，保證算法能有效進(jìn)行全局搜索，探索解的位置信息。但隨著迭代次數(shù)增加，算法的擾動(dòng)性不斷降低，保證迭代后期算法能有效開(kāi)展局部搜索，完成解的收斂。自適應(yīng)參數(shù)更新策略的數(shù)學(xué)表達(dá)式如下：

ES=kπ6×r3×（arccos（tT））（12）

式中：k是擾動(dòng)控制系數(shù)，本文實(shí)驗(yàn)中取值為2.5；t是當(dāng)前迭代次數(shù)；T是最大迭代次數(shù)；r3∈［-1，1］。

改進(jìn)后的ES參數(shù)隨迭代次數(shù)的信息變化過(guò)程如圖2所示。可以發(fā)現(xiàn)，改進(jìn)后該參數(shù)隨迭代時(shí)間呈現(xiàn)出非線性變化，后期震蕩范圍減小。

2.4LERSA算法實(shí)現(xiàn)流程

LERSA算法流程圖如圖3所示。

步驟1：初始化鱷魚(yú)種群數(shù)目N，迭代次數(shù)T，求解問(wèn)題的維數(shù)D以及參數(shù)β，α；

步驟2：使用精英反向?qū)W習(xí)策略初始化種群；

步驟3：計(jì)算種群個(gè)體的適應(yīng)度信息；

步驟4：計(jì)算自適應(yīng)參數(shù)ES;

步驟5：結(jié)合Levy飛行策略更新個(gè)體位置信息；

步驟6：判斷個(gè)體位置信息是否越界；

步驟7：判斷迭代是否結(jié)束，未結(jié)束則重復(fù)步驟3-步驟6。

3實(shí)驗(yàn)仿真與結(jié)果分析

為驗(yàn)證LERSA算法的性能，選擇公開(kāi)的測(cè)試函數(shù)進(jìn)行驗(yàn)證。為提升實(shí)驗(yàn)說(shuō)服力，選擇對(duì)比算法為蟻獅算法（Ant lion optimizer， ALO）［16］、正余弦算法（Sine cosine algorithm， SCA）［17］、樽海鞘優(yōu)化算法（SSA）、粒子群優(yōu)化算法（Particle swarm optimization， PSO）［18］和RSA算法。其中ALO和SSA均為模擬相關(guān)生物捕食行為的仿生算法，該類算法在對(duì)比實(shí)驗(yàn)中較為常用。SCA是具有代表性的基于數(shù)學(xué)模型提出的一種優(yōu)化算法。PSO是經(jīng)典優(yōu)化算法，為重要的對(duì)比算法。相關(guān)實(shí)驗(yàn)算法的重要參數(shù)設(shè)置如表1所示。

對(duì)比實(shí)驗(yàn)測(cè)試函數(shù)采用CEC常用的23組基準(zhǔn)測(cè)試函數(shù)［19］。該組函數(shù)涵蓋三類，分別是單峰測(cè)試函數(shù)（f1-f7）、多峰測(cè)試函數(shù)（f8-f13）和固定維多峰測(cè)試函數(shù)（f14-f23），具體函數(shù)名稱、維度、最優(yōu)值見(jiàn)參考文獻(xiàn)［19］。

3.1算法性能測(cè)試

對(duì)比實(shí)驗(yàn)種群大小設(shè)置為30，最大迭代次數(shù)設(shè)置為500。為防止偶然實(shí)驗(yàn)的影響，本文的平均值和標(biāo)準(zhǔn)差由算法獨(dú)立實(shí)驗(yàn)30次得到。實(shí)驗(yàn)測(cè)試函數(shù)為 f1-f15。結(jié)果表明，不同測(cè)試函數(shù)不同算法的實(shí)驗(yàn)結(jié)果存在差異。

測(cè)試函數(shù)f1-f7主要用于測(cè)試算法的局部搜索能力。在f1，f2，f3，f4上，RSA算法和LERSA算法均可以找到全局最優(yōu)解，對(duì)于兩者性能評(píng)估需要結(jié)合其他評(píng)價(jià)方式進(jìn)行后續(xù)分析，而其他算法無(wú)法有效找到全局最優(yōu)解。f5和f7測(cè)試函數(shù)的實(shí)驗(yàn)說(shuō)明LERSA 算法能有效找到全局最優(yōu)解，f6測(cè)試函數(shù)的實(shí)驗(yàn)結(jié)果LERSA算法表現(xiàn)相對(duì)較差。綜合來(lái)看，改進(jìn)后的LERSA算法具有更好的局部搜索性能，它能有效找到目標(biāo)測(cè)試函數(shù)的全局最優(yōu)解。

測(cè)試函數(shù)f8-f15主要用于全局搜索能力測(cè)試。在函數(shù)f9，f10，f11上，LERSA算法與RSA算法都能有效找到全局最優(yōu)解。在其他測(cè)試函數(shù)上，LERSA算法的標(biāo)準(zhǔn)差更小，表明改進(jìn)后算法的穩(wěn)定性更強(qiáng)。綜合來(lái)看，與對(duì)照算法相比較，改進(jìn)后的算法穩(wěn)定性更好，搜索能力更強(qiáng)。由于篇幅限制，此處展示具有代表性的f1和f13實(shí)驗(yàn)結(jié)果，如表2所示，其他測(cè)試函數(shù)詳細(xì)實(shí)驗(yàn)數(shù)據(jù)略。

算法的收斂速度是評(píng)判算法效率的有效指標(biāo)。從對(duì)比實(shí)驗(yàn)的結(jié)果來(lái)看，雖然部分算法在某些測(cè)試函數(shù)上可以探索到函數(shù)的全局最優(yōu)解，但是算法所需要的時(shí)間資源開(kāi)銷(xiāo)遠(yuǎn)高于LERSA算法。由實(shí)驗(yàn)結(jié)果可知，在函數(shù)f1-f7，f9-f11和f13中，LERSA收斂速度和精度優(yōu)于其他算法；在f8和f12中，收斂速度優(yōu)于其他算法，但收斂精度排第二，略遜于RSA。

本文僅展示了f1和f13的收斂曲線，如圖4所示，其他函數(shù)詳細(xì)實(shí)驗(yàn)圖略。從實(shí)驗(yàn)結(jié)果可知RSA和LERSA算法都可以探索到全局最優(yōu)解，但結(jié)合收斂曲線可以發(fā)現(xiàn)改進(jìn)算法LERSA的收斂速度更快，能更快逼近全局最優(yōu)解。

綜合實(shí)驗(yàn)結(jié)果可知，本文所提出的LERSA算法具有較高的收斂精度，同時(shí)具有相對(duì)較快的收斂速度。結(jié)合收斂曲線和實(shí)驗(yàn)數(shù)據(jù)可以發(fā)現(xiàn)LERSA算法具有較好的性能。

3.2改進(jìn)策略貢獻(xiàn)度消融分析

LERSA算法具有較好的算法性能，但該算法使用3種策略進(jìn)行性能優(yōu)化。所以，分析3種改良策略對(duì)算法性能貢獻(xiàn)的多少是必不可少的實(shí)驗(yàn)環(huán)節(jié)。為方便實(shí)驗(yàn)分析，本文只討論單一優(yōu)化策略的性能貢獻(xiàn)，并將3種不同策略優(yōu)化的RSA算法進(jìn)行統(tǒng)一標(biāo)注。其中，基于精英反向種群初始化策略的RSA算法標(biāo)記為ERSA算法；將基于Levy飛行個(gè)體位置更新策略的RSA算法標(biāo)記為L(zhǎng)RSA算法；基于自適應(yīng)參數(shù)更新策略的RSA算法標(biāo)記為IRSA算法。貢獻(xiàn)度分析展示局部極值相對(duì)較多的f4和f13，如圖5所示，其他測(cè)試詳細(xì)實(shí)驗(yàn)結(jié)果圖略。

Levy飛行策略的優(yōu)化效果略優(yōu)于自適應(yīng)參數(shù)和精英反向種群優(yōu)化策略，但每一種更新策略都為RSA算法的優(yōu)化做出了正向貢獻(xiàn)。綜合來(lái)看，本文所提出的LERSA算法的3種改良策略都可以在一定程度上提升RSA算法的性能，因此改良策略是有效的。

3.3時(shí)間復(fù)雜度分析

設(shè)RSA算法的種群規(guī)模為N，問(wèn)題的維度為D，最大迭代次數(shù)為T(mén)，初始化時(shí)間復(fù)雜度為O（N），位置更新復(fù)雜度為O（T×N）+O（T×N×D），則RSA的時(shí)間復(fù)雜度為O（N×（T×D+1））。

對(duì)于LERSA算法，精英反向種群初始化策略的時(shí)間復(fù)雜度為O（N），使用Levy飛行策略更新個(gè)體位置后，個(gè)體位置信息更新的時(shí)間復(fù)雜度為O（T×N）+O（T×N×D），同時(shí)因?yàn)樽赃m應(yīng)非線性加權(quán)參數(shù)只需要計(jì)算數(shù)值，沒(méi)有引入額外的遞歸操作，因此該策略不會(huì)增加額外的時(shí)間復(fù)雜度。可以發(fā)現(xiàn)LERSA算法的時(shí)間復(fù)雜度為O（N×（T×D+1）），與RSA算法的時(shí)間復(fù)雜度保持一致，改良策略并沒(méi)有消耗更多的實(shí)際資源。

3.4Wilcoxon秩和檢驗(yàn)

算法性能優(yōu)劣僅使用平均值和標(biāo)準(zhǔn)差來(lái)衡量是不夠嚴(yán)謹(jǐn)?shù)模?0］，本文使用Wilcoxon秩和檢驗(yàn)進(jìn)一步測(cè)試算法性能。

本文以23個(gè)測(cè)試函數(shù)做秩和檢驗(yàn)實(shí)驗(yàn)，分析結(jié)果可以發(fā)現(xiàn)，f15結(jié)果說(shuō)明LERSA算法與ALO算法、SCA算法和SSA算法的秩和檢驗(yàn)值大于5%，函數(shù)f1，f2，f3，f4，f9，f10和f11的實(shí)驗(yàn)結(jié)果為NaN，表明這些情況下，秩和檢驗(yàn)不適用，原因是兩種算法均能搜索到最優(yōu)解；其他函數(shù)上不同算法的實(shí)驗(yàn)結(jié)果均小于5%，說(shuō)明LERSA具有良好性能。詳細(xì)實(shí)驗(yàn)數(shù)據(jù)略。

4工程實(shí)例驗(yàn)證——三桿桁架設(shè)計(jì)問(wèn)題

三桿桁架問(wèn)題是測(cè)試優(yōu)化算法性能的實(shí)際工程問(wèn)題，該問(wèn)題具有較強(qiáng)的代表性，對(duì)算法性能要求較高，因此本文選擇該問(wèn)題驗(yàn)證改良算法LERSA對(duì)實(shí)際工程問(wèn)題的優(yōu)化性能。三桿桁架問(wèn)題概要圖如圖6所示。

該問(wèn)題的預(yù)期目標(biāo)為重量最小，數(shù)學(xué)表達(dá)式如下：

minf（x）=（2x1+x2）×l（13）

s.t. g1（x）=2x1+x22x21+2x1x2P-σ0（14）

g2（x）=x22x21+2x1x2P-σ0（15）

g3（x）=12x2+x1P-σ0（16）

式中：0xi1，i=1，2；l=100 cm；P=2 kN/cm2；σ=2 kN/cm2。

在已有研究中，三桿桁架問(wèn)題使用的優(yōu)化解決方案有布谷鳥(niǎo)搜索算法（Cuckoo search algorithm， CS）［21］、算術(shù)優(yōu)化算法（Arithmetic optimization algorithm， AOA）［22］、粒子群差分進(jìn)化（Particle swarm optimization-Differential evolution， PSO-DE）［23］、飛蛾撲火算法（Mothflame optimization， MFO）［24］、蝗蟲(chóng)優(yōu)化算法（GOA）和樽海鞘優(yōu)化算法（SSA）等，本文將上述算法作為對(duì)照驗(yàn)證LERSA在解決該問(wèn)題時(shí)的性能。

保持相同實(shí)驗(yàn)條件進(jìn)行對(duì)照實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果如表3所示。可以發(fā)現(xiàn)，LERSA算法在求解三桿桁架設(shè)計(jì)問(wèn)題時(shí)的性能略優(yōu)于其他算法。

5結(jié)束語(yǔ)

本文使用精英反向?qū)W習(xí)策略提高初始化種群質(zhì)量、Levy飛行改良種群的個(gè)體更新策略，結(jié)合非線性加權(quán)調(diào)節(jié)控制參數(shù)，提出一種改進(jìn)的爬行動(dòng)物搜索算法。實(shí)驗(yàn)證明，與當(dāng)前流行的其他算法對(duì)比，改進(jìn)后算法的綜合性能較優(yōu)，并在三桿桁架問(wèn)題上取得了較好結(jié)果。改進(jìn)的爬行動(dòng)物搜索算法能有效解決工程優(yōu)化問(wèn)題，為工程優(yōu)化問(wèn)題提供了一種更優(yōu)的解決方案。

參考文獻(xiàn)

［1］ABUALIGAH L， ELAZIZ M A， SUMARI P， et al. Reptile search algorithm （RSA）： A natureinspired metaheuristic optimizer［J］. Expert Systems with Applications， 2022， 191： 116158.

［2］SAREMI S， MIRJALILI S， LEWIS A. Grasshopper optimisation algorithm： theory and application［J］. Advances in Engineering Software， 2017， 105： 30-47.

［3］MIRJALILI S， MIRJALILI S M， LEWIS A. Grey wolf optimizer［J］. Advances in Engineering Software， 2014， 69： 46-61.

［4］FARAMARZI A， HEIDARINEJAD M， MIRJALILI S， et al. Marine predators algorithm： A natureinspired metaheuristic［J］. Expert Systems with Applications， 2020， 152： 113377.

［5］DUAN Q， WANG L， KANG H W， et al. Improved salp swarm algorithm with simulated annealing for solving engineering optimization problems［J］. Symmetry， 2021， 13（6）： 1092.

［6］ALMOTAIRI K H， ABUALIGAH L. Hybrid reptile search algorithm and remora optimization algorithm for optimization tasks and data clustering［J］. Symmetry， 2022， 14（3）： 458.

［7］JIA H M， PENG X X， LANG C B. Remora optimization algorithm［J］. Expert Systems with Applications， 2021， 185： 115665.

［8］EL SHINAWI A， ALI IBRAHIM R， ABUALIGAH L， et al. Enhanced adaptive neurofuzzy inference system using reptile search algorithm for relating swelling potentiality using index geotechnical properties： a case study at el sherouk city， Egypt［J］. Mathematics， 2021， 9（24）： 3295.

［9］付華，許桐，邵靖宇.基于水波進(jìn)化和動(dòng)態(tài)萊維飛行的爬行動(dòng)物搜素算法［J/OL］.控制與決策， 2023： 1-9.（2023-05-02）. http：//kzyjc.alljournals.cn/kzyjc/article/abstract/2022-0647.

［10］李新華， 崔東文. 基于WPD-RSA-ELM模型的水文時(shí)間序列多步預(yù)測(cè)［J］. 水利水電技術(shù)（中英文）， 2022， 53（11）： 69-77.

［11］EKINCI S， IZCI D， ABU ZITAR R， et al. Development of Lévy flightbased reptile search algorithm with local search ability for power systems engineering design problems［J］. Neural Computing and Applications， 2022， 34（22）： 20263-20283.

［12］HUANG L Q， WANG Y Y， GUO Y X， et al. An improved reptile search algorithm based on Lévy flight and interactive crossover strategy to engineering application［J］. Mathematics， 2022， 10（13）： 2329.

［13］WEI W H， ZHOU J L， CHEN F， et al. Constrained differential evolution using generalized oppositionbased learning ［J］. Soft Computing， 2016， 20（11）： 4413-4437.

［14］ZHOU Y Q， WANG R， LUO Q F. Elite oppositionbased flower pollination algorithm［J］. Neurocomputing， 2016， 188： 294-310.

［15］HOUSSEIN E H， SAAD M R， HASHIM F A， et al. Lévy flight distribution： A new metaheuristic algorithm for solving engineering optimization problems［J］. Engineering Applications of Artificial Intelligence， 2020， 94： 103731.

［16］MIRJALILI S. The ant lion optimizer［J］. Advances in Engineering Software， 2015， 83： 80-98.

［17］MIRJALILI S. SCA： a Sine Cosine Algorithm for solving optimization problems［J］. KnowledgeBased Systems， 2016， 96： 120-133.

［18］WANG D S， TAN D P， LIU L. Particle swarm optimization algorithm： an overview［J］. Soft Computing， 2018， 22（2）： 387-408.

［19］SUGANTHAN P N， HANSEN N， LIANG J J， et al. Problem definitions and evaluation criteria for the CEC 2005 special session on realparameter optimization［J］. Natural Computing， 2005： 341-357.

［20］DERRAC J， GARCA S， MOLINA D， et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms［J］. Swarm and Evolutionary Computation， 2011， 1（1）： 3-18.

［21］GANDOMI A H， YANG X S， ALAVI A H. Cuckoo search algorithm： a metaheuristic approach to solve structural optimization problems［J］. Engineering with Computers， 2013， 29（1）： 17-35.

［22］ABUALIGAH L， DIABAT A， MIRJALILI S， et al. The arithmetic optimization algorithm［J］. Computer Methods in Applied Mechanics and Engineering， 2021， 376： 113609.

［23］LIU H， CAI Z X， WANG Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization［J］. Applied Soft Computing， 2010， 10（2）： 629-640.

［24］MIRJALILI S. Mothflame optimization algorithm： A novel natureinspired heuristic paradigm［J］. KnowledgeBased Systems， 2015， 89： 228-249.